在数学活动中感悟问与学的魅力

赵萍萍

摘 要：以探究式的教学模式，实现“基于问题、问学融合”的教学主张，使学生获得有意义的学习和有深度的学习。

关键词：问学;活动;一题多变

问学，即“基于问题的学习”，美国最权威的Wikipedia在线百科全书将其定义为“一种以学生为中心的教学策略，学生通过合作解决问题并反思其学习经验”。笔者所在学校正进行着“普通初中‘问学课堂教学模式的校本建构研究”的课题研究，旨在教学操作上突出“问”对“学”策略性作用和素养培育上突出“问”对“学”的深化作用，概括为“问以致学、学以致用、用以致能、学会学习”。基于此，数学学科进行了大量的课堂教学形态的探索，通过开发探究式的教学模式，实现“基于问题、问学融合”的教学主张，使学生获得有意义的学习和有深度的学习。下面以《初一数学“一题多变”训练活动方案》谈一点认识。

一、活动的提出

苏科版教材第七章《平面图形的认识（二）》是学生在初步接触几何图形后，开始研究图形的形状、大小和位置关系。在这一阶段，对图形认知的要求更高，而传统的讲授式教学模式，重复低效解题、解题、再解题，使相当一部分学生“丧失”了数学学习的兴趣，不想提问不会提问。思维变得狭窄，学知识只知其一，不知其二，不会举一反三，做不到触类旁通，解决问题的能力得不到提升。因此，在这个关键时期，开展一题多变的活动形式，有助于培养他们的观察能力，激发他们提出问题的兴致，帮助他们克服思维狭窄性的有效方法。

二、活动的目的

1.通过一题多变，培养学生的发散思维能力及相关知识点迁移能力;学生大胆设疑，能扩大学生知识容量，并培养面对难题的从容心态。

2.通过一个普通数学题的“变化”，让学生总结、发现和体会问题之间的联系，学会自主解决问题。

三、活动的重点

通过活动培养学生的问题意识、创新能力和从特殊到一般的归纳方法。

四、活动的时间

45分钟。

五、活动的过程

1.活動准备：让学生回顾平行线的性质和判定，通过演示课件，回顾一些熟悉的题目。

【活动说明】通过对本章内容的一个整体回顾，让学生感知活动内容均来源于他们的已有知识，从而充满期待和好奇。

2.活动探究：

活动1 一变：命题的条件与结论

如图1，CD⊥AB，E是BC上一点，EF⊥AB于F，∠GDC=∠FEB。

试说明∠BDG+∠B=180°。

变题：如图1，将①CD⊥AB;②EF⊥AB;③∠1=∠2;④∠BDG+∠B=180°四个论断中的三个作为题设，另一个作为结论，写出对应的命题，并判断真假。

【活动说明】将这个学生熟悉的题目作为活动1，从全方位多角度重新认识这个“老题”。学生在变题的过程中自己设计题目，提出问题，既巩固了对平行线性质和判定的理解及应用，体会到这类题目的本质特征;又具有新鲜感，诱发解题欲望，调动问与学的积极性。

活动2 二变：图形的位置

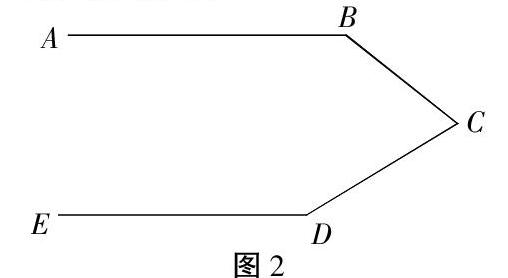
如图2，直线AB∥DE，点C为直线AB和DE外的一点，试寻找出之间的数量关系。

变题：如上图，将点C的位置移到你喜欢的另一个位置（如直线AB的上方等），猜想∠B、∠C、∠D的数量关系并说明。

【活动说明】通过动手实践，自主探索与合作交流，学生不断发现问题、解决问题。在亲身体验和探索了“做数学”的过程后，他们的主体性得到极大的发挥，所学知识在这个过程中不断得以巩固、发展与提升。

活动3 分小组、大组交流——展示

1.小组内同学之间互相交流：分别展示出各自画平行线的方法，说说画图的依据，是如何思考出这种画图方法的？

2.推荐小组优秀代表进行大组交流：可以利用哪些办法画平行线？如何思考的？在画图过程中你积累了什么经验？在各种画图方法的基础上你还发现了什么问题？

【活动说明】安排此环节主要基于以下思考：从发现到表达交流是能力提升的过程，在倾听、思辨、争鸣中统一基本认识还能追求“求同存异”，为提出新的问题提供了生长点。

六、活动的收获

在本节课的探究过程中，你有哪些感受与收获？回顾你的探究心路历程，请将你的探究经验、感悟和发现写成数学小论文。

【活动说明】撰写数学小论文就是以“数学写作活动”来指导学习，也可称为“反思小文章”。它是学生将在问与学的过程中得到的知识、技能、经验、思想方法进行“内化”，是问学课堂的有效延伸。

七、活动的评价

【活动说明】数学探究性学习的评价应突出过程性评价。重点评价自己在探究过程中对问题的理解、思辨与情感态度的投入程度，也要学会倾听同学、老师的意见，提高问学效率。

课堂教学形态的变革是一个渐近的、潜移默化的、长期的过程，设计教学要多元化，以培养学生的问题意识、促进学生的深度学习为指导，让课堂成了师生共同提出问题、分析问题、解决问题的主阵地，从而激励学生积极主动地学习，生动活泼地参与课堂研究。只有这样的课堂，才能全面提高学生的科学素养，使课堂教学真正从应试教育向素质教育转化。

编辑 温雪莲