剪切转换区模型探究二维非晶合金的准静态剪切应变
(1.上海交通大学材料科学与工程学院,上海 200240; 2.上海交通大学物理与天文学院,上海 200240; 3.上海交通大学数学系,上海 200240)
1 前 言
非晶固体在自然界中广泛存在[1],然而与晶体相比,非晶固体的塑性形变微观机制一直没有很完善的解释[2-3]。非晶固体塑性应变在微观上最明显的特征是,当对非晶材料施加应力加载时,非晶固体不会发生类似晶体材料中的位错滑移,而是通过局部原子的重排来适应剪切应变。关于非晶固体的塑性流动和变形机制所建立的力学理论众多,其中Argon提出的与应变匹配的局部重排的剪切转换理论,是著名的均匀塑性流和非均匀的塑性流假设[4]。塑性流的基本单元是剪切转变区(STZ),或是局部自由体积的扩散跃迁[5]。STZ是一小簇紧密的原子,会自发协同重排以适应外加切应变,当局部原子簇经受急剧扭曲时,原子簇会从初始平衡态经过高能量的中间态,最终到达另一个平衡态。一个STZ的重排会造成周围原子的局域化扭曲,当外部应力加载进一步进行,会引发更多STZ的生成,最终形成STZ大量聚集的区域,被称为剪切带(shear band)。值得强调的是STZ并不是非晶固体结构里的缺陷,而是受局部原子重排影响的一种密度较低的过渡状态。Spaepen在自由体积模型的基础上建立了塑性流理论,提出形变的发生是一系列局部的原子跃迁到具有较大自由体积的空位处这一类似扩散的过程[6]。几十年来研究者们提出了针对这两个模型改进方法[7],但Spaepon和Argon提出的模型直至目前仍是描述非晶固体形变模型中最被广泛认可的理论模型。
Langer和Falk等[2,8-12]在对非晶合金的粘塑性变形进行分子动力学模拟研究时,不仅观察到了这种STZ流变事件,而且还发展了Argon的STZ模型,通过模拟结果引入了STZ数密度作为塑性变形的内变量,从而了解到STZ在弹性固体的环境中会产生波动,随着时间的变化会生成和消失。当STZ存在时,它们经历不可逆的重排,并因此响应于应力而产生塑性变形。这个理论已被广泛讨论[10],并在剪切带、断裂韧性和振荡粘弹性等理论中得到广泛应用。近年来也有采用三维STZ几何模型来验证该理论的实验[13-14]。
张洁[15]对宏观无序颗粒材料剪切试验结果采用STZ模型对所有颗粒的几何信息进行分析,并与实验过程中的力学数据作对比,结果发现STZ模型与应力应变曲线具有很紧密的联系,表明STZ模型在描述宏观无序材料的形变力学性质中具有一定的可靠性。
本研究中所做的分子动力学实验的工作是基于该宏观颗粒材料实验的思想。在微观尺度,使用分子动力学方法,对不同组分的二维CuZr合金做剪切应变的实验,然后采用简化的二维STZ模型,对模拟结果进行几何结构上的分析,并与分子动力学实验得出的应力应变关系进行对比,从而验证STZ模型在描述塑性形变过程的可靠性,同时得出应力变化与STZ生成和消失的关系。
2 实验方法
2.1 分子动力学实现剪切实验
本工作目的是探究STZ理论与剪切带成因,由于数学模型采用简化的二维STZ四边形模型,所以这里数值实验也选取二维的金属玻璃样品 CuxZry单相非晶开始展开模拟和分析[16-19]。同时,该二维的CuZr合金模型使用EAM势能作为分子间相互作用势能,与三维的分子模型相比,该二维模型可以很好地模拟非晶合金的力学性质。为了力求清晰、多角度地描述CuxZry单相非晶中剪切带的生长过程,使用常用的快速冷却法构建X、Y方向为周期性边界条件的二维非晶模型[20-21],数值计算工具为LAMMPS[22-23]。
图1(a)是在LAMMPS中,使用快速冷却法,制备的二维的Cu50Zr50金属玻璃模型,共计10000个原子,Cu、Zr原子各5000个,原子半径比为117∶145,近似为1∶1.24,原子势能使用EAM势能。然后,在微正则系综条件下,在XY平面内做简单剪切的加载,应变率为107s-1,沿Y轴方向准静态压缩,至工程应变为20%,共计20 ns,见图1(b)。

图1 非晶材料剪切实验示意图(a)为二维Cu50Zr50非晶材料样品,Cu原子标为蓝色,Zr原子标为红色;(b)为施加的应变和压强示意图,Y轴方向施加恒定的应变率,X轴方向施加恒定的压强(本刊黑白印刷,欲知颜色直接联系作者)Fig.1 Schematic diagram of shearing test of amorphous materials(a)Snapshot of 2D Cu50Zr50 metallic glass film, Cu-atoms are shown as blue balls, Zr-atoms are red; (b) View of strain and compress applied on the sample, constant strain rate in Y-axis direction, constant pressure in X-axis direction
在这个形变过程的数值实验中,记录每个粒子的编号、类型、坐标、X和Y方向的应力[22],并生成均匀时间间隔的200帧图像来储存这些粒子的信息。其中每个粒子都有自己单独的编号,会全程追踪其运动行为,粒子类型是指是区分粒子为Cu或Zr原子,坐标是粒子在XY平面的坐标。
2.2 STZ的二维简化模型
首先定义二维STZ四边形[24-25]。对于一个二维的非晶固体材料,对每个原子都搜索与其最近邻的两个原子,如图2中,D原子近邻的两个原子为A和B,然后搜索A和B原子的近邻原子并比较,如果有共同存在C原子为A和B原子共同的近邻原子,则定义该四边形ABCD是满足要求的STZ四边形。

图2 STZ的示意图,图中A、B、C、D分别为粒子的中心Fig.2 Schematic diagram of STZ, A、B、C、D are the center of atoms
然后定义T1事件(T1-event)[24-25]。为了方便表达,定义T1-event为STZ四边形完成一次由CD原子近邻到AB原子近邻的转变,见图3。
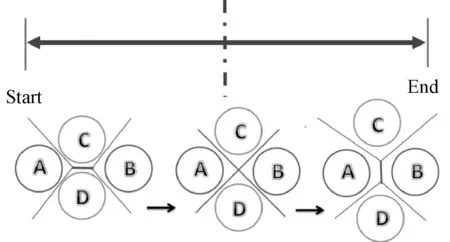
图3 T1事件的定义,STZ经历了一次由CD原子近邻到AB原子近邻的转变Fig.3 Definition of T1-event, the nearest neighbor atoms have changed from CD to AB in STZ
2.3 STZ四边形的程序实现方法
为了找出全部实验过程中的每一帧图中所有的发生了T1-event的STZ四边形,为计算程序的设计以下思路。
第一步:粒子跟踪。

第二步:搜索STZ四边形。
根据STZ四边形的定义,找出每帧图像中所有存在的STZ四边形。具体方法是,遍历每个粒子,搜索与其最近邻的两个原子,此时需要依赖粒子的半径信息。每找出一个STZ四边形,在程序中记录STZ四边形数量Numstz加一,并给该STZ四边形按顺序编号N。如果该粒子没有搜索到满足要求的四边形则继续搜索下一个粒子,如果搜索到存在多个四边形共用该粒子,也要将每个四边形依次记录下来。最终会得到每帧图中所有满足条件的STZ四边形,用四个顶点的粒子编号stzN=(n1,n2,n3,n4)来标记。而且每张图都需要和前一张图作对比,若产生了全新的STZ,则需要赋予新的编号,用链表记录。
第三步:STZ四边形的演化跟踪。
对每一个编号的STZ四边形,在其存在的图片中计算它的对角线长度之比,顶点为每个粒子的坐标,见图4:
(1)
如果前后两帧图像中的相同编号的STZ四边形发生了最近邻原子变为次近邻原子的转变,即Ratio从大于1变为小于1或反之,则说明该STZ发生了一次T1-event,可以通过判断(RatioNstz,F+1-1)*(RatioNstz,F-1)<0来确定。

图4 根据线段AB与CD的比值变化判断T1事件的发生,图中A、B、C、D分别为粒子的中心Fig.4 Change of the ratio of AB and CD is the determination method of T1-event, A、B、C、D are the center of atoms
最后一步:作图。
遍历整个过程,将发生了的T1-event的STZ四边形在每张图中的位置记录下来,方法是记录四边形的四个顶点的粒子编号stzN=(n1,n2,n3,n4)和坐标信息(xn1~4,F,yn1~4,F),然后依次绘图,即可看到在整个过程中样品体系中STZ的演化过程,也可以看到每一步实验步骤中STZ在整体样品中的分布。
3 实验结果
3.1 分子动力学实验
首先根据粒子应力信息,可以清晰地分辨出样品Cu50Zr50在形变过程中分为弹性形变阶段和塑性形变阶段。图5中,在初始状态到形变率达到3.6%的阶段,随着应变的增加,应力一直在上升,为弹性形变阶段。之后应力维持在一个范围内波动,为塑性形变阶段[26-28]。

图5 样品的应力应变分布,虚线右边为弹性形变阶段,左边为塑性形变阶段Fig.5 Stress-strain curves of sample, right side of the dotted line is during elastic deformation stage, left side of the dotted line is during plastic deformation stage
根据所记录的粒子的坐标信息,还可以绘制出粒子的位移场,∈为应变量,为了清楚地看到位移矢量,图中没有显示原子。图6(a)中,∈=0.02,为第20帧,此时在弹性阶段,位移场显示出粒子还没有明显的运动规律。图6(b)中,∈=0.05,为第50帧,此时刚进入塑性形变阶段,可以看到在剪切带的局部带状区域内粒子已经开始形成涡流。图6(c)、(d)中,∈分别是0.07和0.13,为第70帧和130帧,可以清晰地看到塑性涡流。从位移场中可以看出以剪切带为分界的大范围反方向协同运动的确存在于非晶的塑性变形中。

图6 原子从初始参考态至各个时刻的位移场,用箭头表示,∈为样品的应变量 (a)∈=0.02,(b)∈=0.05,(c)∈=0.07,(d)∈=0.13,(e)为图(d)的局部放大图Fig.6 Atomic displacement fields from the reference state to the current states, displacement vectors are indicated as blue arrows, ∈ is the strain. Image (e) is the detail view of image (d)(a)∈=0.02, (b)∈=0.05, (c)∈=0.07, (d)∈=0.13, (e) is the detail view of image (d)
3.2 二维STZ模型对分子动力学实验结果的分析
这些数据中,STZ模型只依赖于每个粒子的编号、类型和坐标。因此只调用这些数据来标定STZ和搜索T1-event。

图7 发生T1-event的STZs在各时刻的分布图(∈为样品的应变量) (a)∈=0.02; (b)∈=0.05; (c)∈=0.07; (d)∈=0.13Fig.7 Distribution of STZs that is during T1-event from the reference state to the current states.∈ is the strain (a)∈=0.02; (b)∈=0.05; (c)∈=0.07; (d)∈=0.13
根据第二节介绍的程序方法,对Cu50Zr50合金实验结果的每一帧粒子的坐标分布图标定出STZ,并对全局进行分析后,搜索出所有满足条件的T1-event,最后在每帧图中标记出正在发生T1-event的STZ四边形,从而得到图7的结果。为了清晰的观察STZ的分布,图7中隐去了粒子,图中的四边形为所有正在发生T1-event的STZ。图7(a)为弹性形变阶段,∈=0.02,是第20帧的STZ四边形的分布,从图可见图中的四边形数量稀少且均匀的分布在样品之中。图7(b)~(d)分别为第50帧、70帧和130帧的STZ分布,可以看到STZ集中倾斜分布在与水平方向呈45°的两条狭长带状区域,这是由实验样品采用的是周期性边界条件生成的原因所导致。
4 分析讨论
把每帧图中所找到的正在发生T1-event的STZ四边形的数量绘制成折线图(见图8),并且把剪切过程中,样品的应力应变曲线也绘制到同一张图表中。从图可见,在 ∈<0.036的弹性形变阶段,即前36帧图像期间,随着应变的增大,应力也在逐渐增加,而发生T1-event的STZ四边形数目并没有显著增加,而是保持在一个平稳的数目附近[29]。

图8 应力应变曲线与发生T1-event的STZ数目曲线Fig.8 Stress-strain curves and total number of STZ during T1-event by strain
当模型进入塑性形变阶段瞬间,发生T1-event的STZ四边形的数目也大幅增加。根据STZ模型的理论,无序固体材料在塑性形变的过程中,是这些STZ单元所发生的T1-event来承载了应力的分布。每个STZ单元在应力作用下,从初始的四边形状态逐步被拉伸或者压缩,在吸收充分的能量后,会翻过中间态能垒,在几何形态上则是发生了一次四边形长短对角线的互换,从而完成了一次T1-event。
在塑性形变阶段,可以从图8中观察到,发生T1-event的STZ的数目,和应力呈现出一定的负相关性。而且每当系统T1-event的数量到达极大值或极小值时,应力的大小也几乎处在极大值或极小值。根据STZ理论不难解释,发生这种T1-event的STZ四边形的数目越多,表明样品当前的体系内部越不稳定,处在相对容易发生形变的状态。当发生的T1-event数量增大的时候,表明体系越来越“松动”,此时,维持恒定应变所需要应力就会逐渐变小。反之,当发生T1-event数量减小时,表明体系越来越“坚韧”,此时,维持恒定应变所需要的应力就会逐渐增大。
把样品在塑性阶段从第41帧到140帧的数据提取出来分析两条曲线的相关性,见图8中虚线框部分。
(2)

计算得到:r=-0.3456。
根据统计上的相关性分析可知,相关性系数的绝对值在0.4~0.6之间,属于具有较好的相关性,若该值过小,不能较好地体现相关性。在结合实际物理意义后,固定T1-event曲线,把应力应变曲线向后平移若干帧,再计算对应的相关性系数,见表1。

表1 固定T1-event曲线,将应力应变曲线向后移动若干帧后的相关性系数Table 1 Fixed T1-event strain curve, move stress-strain curve backwards several frames to calculate correlation coefficient
从表中可以发现,在后移两帧的位置,所得到的结果就是在有相关性的范围中比较优秀的数值。事实上由于实验和算法的不完善,会使实验结果存在误差,而在本实验中,在根据物理意义进行调整后,应力应变曲线与T1-event数量变化曲线的相关性系数依然达到了-0.5797,足以表明两者之间存在很强的负相关性。而且从这个现象可以推测,在实际发生塑性形变的微观过程中,STZ的T1-event形变时间,会稍微早于应力的变化,但最多不会超过每个STZ形变过程所经历的时间的一半。
最后为了验证该实验结果与结论的可靠性,通过改变CuZr 合金的组分,重复以上实验和数值模拟过程,进而得出不同组分的CuZr 合金在应变过程中,应力与T1-event数量的相关性,具体的结果见图9。每个相关性系数均为把应力应变曲线向后平移了1~4帧后取极值的结果。图中结果表明,改变CuZr 合金组分,应力应变曲线与T1-event数量变化曲线的相关性系数依然保持在强负相关性的范围。因此可以肯定STZ模型在描述微观非晶合金材料的形变力学性质中具有一定的可靠性。

图9 不同组分的CuZr 合金在应变过程中,应力与T1-event数量的相关性系数。横轴为Cu原子所占CuZr 合金的比例,纵轴为相关性系数。相关性系数于-0.4~-1之间为强负相关性Fig.9 Correlation coefficient between the stress and the number of T1-event in the CuZr alloy with different composition. The abscissa is the proportion of CuZr alloy occupied by Cu atoms, and the ordinate is the correlation coefficient. The correlation coefficient is between -0.4 and -1 for strong correlation
5 结 论
1.在恒定的应变过程中,发生T1-event的STZ的数目,与加载应力的大小呈现出较好的负相关性。发生这种T1-event的STZ四边形的数目越多,表明样品的体系内部越不稳定,处在相对更易发生形变的状态。当发生的T1-event数量增大时,表明体系越来越“松动”。此时,维持恒定应变所需应力就会逐渐变小。反之,当发生T1-event的数量减小时,表明体系越来越“坚韧”,此时维持恒定应变所需要的应力就会逐渐增大。
2.改变CuZr 合金组分,应力应变曲线与T1-event数量变化曲线的相关性系数依然保持在强负相关性的范围。
3.在实际发生塑性形变的微观过程中,STZ发生T1-event的时间,会略微早于应力的变化,但最多不会超过每个T1-event过程所经历时间的一半。
4.该简化的STZ模型可以很好地解释二维非晶合金在准静态剪切形变中剪切带的成因,值得推广到三维体系进行实验模拟。

