对2019年高考全国III卷理科第21题的探究

重庆市合川中学(401520) 王安国 李娟

一．试题呈现及背景

题目(2019年高考全国I卷理科第21题)已知曲线为直线上的动点，过D作C的两条切线，切点分别为A,B.

(I)证明：直线AB过定点;

分析本题主要考查过抛物线切点的直线方程，直线和圆相切的相关知识，考查灵活运用所学知识，探究问题和解决问题的能力，全面考查学生的数学综合素养.

试题背景此题中的图形，涉及到抛物线的弦与过弦的端点的两条切线所围成的三角形，这个三角形又常被称为阿基米德三角形.阿基米德三角形的得名，是因为阿基米德本人是最早利用逼近的思想证明了如下结论：抛物线的弦与抛物线所围成的封闭图形的面积，等于抛物线的弦与过弦的端点的两条切线所围成的三角形面积的三分之二.普通高中选修课程标准试验教科书数学选修3-1(A版)《数学史选讲》第21页中，有与这个结论相关的另外一种变式叙述.此题为过抛物线焦点的阿基米三角形.

二．解法探究

(I)解法一略(参考答案)

解法二设直线AB的方程为整理得x2-2kx-2b=0，Δ=4k2+8b＞0，则x1x2=-2b.由于y′=x，所以过A的切线方程为

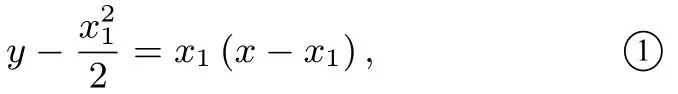
过B的切线方程为

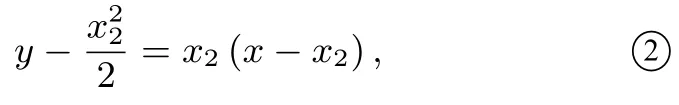
解法三(先猜后证)由抛物线图象关于y轴对称和D点在直线上运动，得到直线AB变化规律，可猜想直线AB的定点落在y轴上.令A(x1,y1)，则切线AD满足方程得则直线AB方程为故得定点坐标为

(II)解法一略(参考答案)

解法二(平面几何解法)

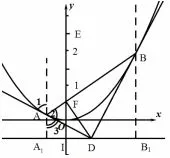
图1

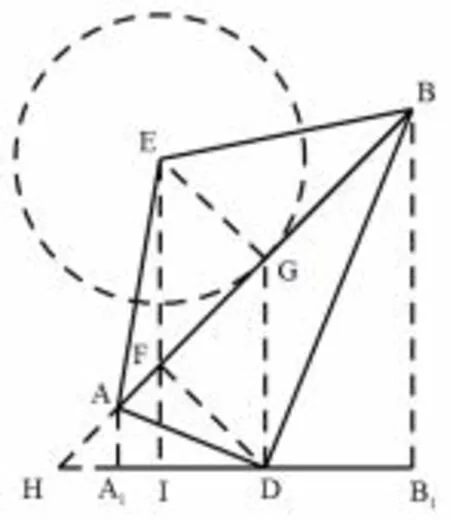
图2

图1中，由抛物线的光学性质易得∠1=∠2，又∠1=∠3，所以∠2=∠3.因为AF=AA1，AD=AD，所以△AFD△AA1D，所以∠AFD=∠AA1D=90°，DF⊥AB，DA1=DF.同理△BDF△BDB1，所以DB1=DF，所以DA1=DB1，即点D为A1B1中点.图2中，已去掉坐标系和抛物线，并延长BA,B1A1于点H.因为GE⊥AB，DF⊥AB，所以GE//DF，又因为G、D分别为AB,A1B1的中点，所以GD//AA1//EF，故EFDG为平行四边形，从而GD=EF=2，AB=AA1+BB1=2GD=4.因为FI//GD且所以I为HD的中点，从而S四边形ADBE=SADB+SABE=当直线AB平行于x轴时，易得S四边形ADBE=3.综上，四边形ADBE的面积为3或

评析相比较于参考答案，试题1(II)中解法二的过程要显得简洁.因为解析几何问题本质是几何问题，它们本身就包含一些很重要的几何性质.如果我们可以充分利用这些几何性质，它们其实就是纯几何问题，完全可以借助平面几何的知识加以解决.这样不但能避开繁琐的代数运算，使解决问题的过程得到简化，而且能更好地揭示这些问题的几何本质.

三．试题的拓展

下面运用平面几何知识，拓展过抛物线x2=2py(p＞0)焦点的阿基米德三角形(如图1)的相关结论.

结论1AD⊥BD，A1F⊥B1F，DF⊥AB;

结论2AD//B1F，A1F//BD;

结论3S△ABD≥p2.

证明图3为过切点作垂直于准线的阿基米德三角形，其本质为“上底加下底等于斜腰的直角梯形”．

(1)由抛物线的定义和试题(II)的求解，容易得到结论1，在Rt△ABD中由射影定理得：DF2=AF·FB.

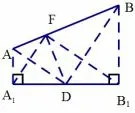
图3

(2)因为△AA1D△ADF，所以AD平分∠A1AF，又AA1=AF，所以AD⊥A1F.因为B1F⊥A1F，所以AD//B1F.同理BD//A1F.

(3)因为ΔAA1D△ADF，△BDF△BDB1，则又其中θ为直线AB的倾斜角，所以

利用上面拓展到的结论容易对试题1进行变式.

变式1F为抛物线y2=2px(p＞0)的焦点，过点F的直线l与该抛物线交于A,B两点，l1,l2分别是该抛物线在A,B两点处的切线，l1,l2相交于点C．设|AF|=a，|BF|=b，则|CF|=____.(2010年“华约”自主招生第4题)

变式2已知抛物线C:y2=2x的焦点为F，平行于x轴的两条直线l1,l2分别交C于A,B两点，交C的准线于P,Q两点．若F在线段AB上，R是PQ的中点，证明AR//FQ.(2016年高考全国III卷理科第20题第一问)

变式3已知抛物线F为抛物线的焦点，过点F的直线l与该抛物线交于A,B两点，l1,l2分别是该抛物线在A,B两点处的切线，l1,l2相交于点D，求三角形ABD面积的最小值.

四．试题的推广

为了方便起见，我们仍以抛物线x2=2py(p＞0)为例，并约定弦AB为阿基米德三角形的底边，A(x1,y1)，B(x2,y2)，F为抛物线的焦点，M为底边的中点，D为两切线的交点.

性质1点D的坐标为

性质2直线AB的方程为(x1+x2)x-2py-x1x2=0;

证明(1)如图4，因为所以过点A的切线方程为

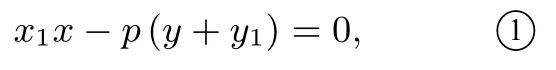
过点B的切线方程为

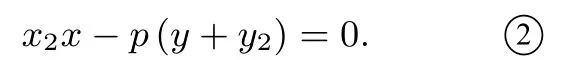
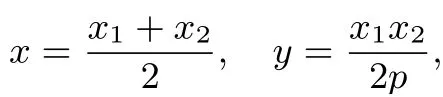
(2)直线AB的斜率为

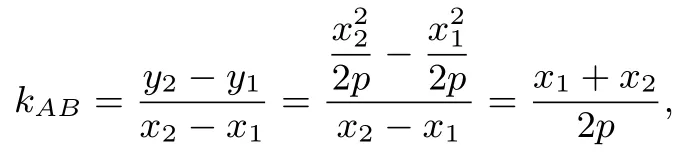
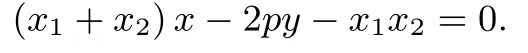
若D(x0,y0)，则直线AB方程x0x-p(y+y0)=0.当D在抛物线准线上运动时，可得直线AB过定点此为试题1(I)的结果.

性质3三角形ABD中，∠DFA=∠DFB;

性质4

性质5若阿基米德三角形底边AB过抛物线内定点C，则另一顶点D的轨迹为一条直线.

注：性质3，4，5的证明读者可参阅文献[2-3].

上述结论反应了阿基米德三角形的相关性质，而它的有关性质已成为高考数学命题的一个藏宝库.在历年的高考试题中都能找到它的身影，例如2005年高考江西卷理科第22题，2007年高考江苏卷理科第17题，2008年高考山东卷理科第22题，2011年高考安徽卷理科第21题等.

五．对今后教学的启示

在解析几何的教学中，利用平面几何知识解决解析几何问题，不但可以避开繁琐的代数运算，简化解题过程，而且解法简洁优美，更好地体现了圆锥曲线的几何性质.

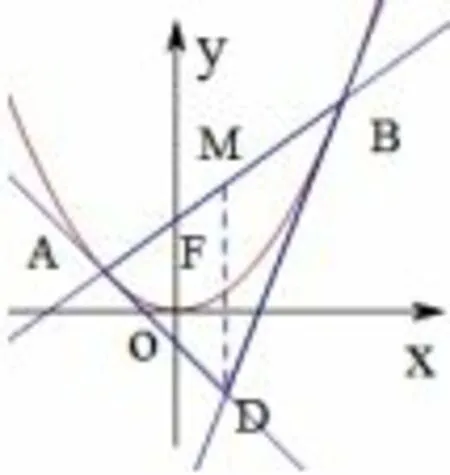
图4

因此对于解析几何问题，不应一味地运用解析法，而应该将解析法和平面几何方法相结合，从而得到解决问题的最优解法，同时可以更好地提高解题能力.

高考试题具有深刻的知识背景，我们要加强对高考试题的探究，对其一般性进行推广，这对于拓展解题思路和寻求更多的解题方法是大有裨益，所以应该提倡对高考试题的研究.同时笔者认为，抓标务本才是真!标即课程标准和考试说明，本就是课本.教师要认真钻研教材，充分发挥教材课本试题的示范性、典型性及探究性功能.高三的复习中，教师在试题评讲时，不应该盲目追求试题繁而多，而应该追求试题精而细，讲清楚试题的内涵与外延，通过一题多解、一题多变，让学生掌握问题的本质，总结做题的思想方法，从而提高复习的效率，最终达到事半功倍的效果.