浅水与桩靴对海上平台水动力影响的数值模拟

(1.武汉理工大学 a.高性能舰船技术教育部重点实验室；b.交通学院，武汉 430063；2.江苏海艺船舶科技有限公司，江苏 镇江 212000)

海上风电作业平台在迁航或移位时，所处水域水深较浅，平台所受阻力增大[1-3]，还会受到因水底存在产生的抽吸力[4]。浅水阻力影响平台移位和就位性能及拖船布置方案；抽吸力造成平台下蹲[5-6]，严重影响平台的安全性。考虑目前海上平台在初步设计过程中，水动力的确定往往参考船舶的大数据。该自升式海上平台与船舶外形具有较大差异，特别是自升式海上平台携带桩腿桩靴，移位时桩靴缩进平台内专用的桩孔内，而船舶外形光滑。桩孔和桩靴的存在对平台水动力大小的影响，引起海上平台专业设计者的关注[7]。鉴于对自升式海上风电作业平台水动力的浅水和桩靴影响研究报道比较缺乏，考虑采用CFD方法，对一座自升式海上风电作业平台，讨论水深变化和不同外形对其水动力的影响。讨论浅水影响时，选取实际有桩靴平台模型，对不同水深、不同流速时的流场进行数值模拟，分析阻力系数和抽吸力系数的变化规律。讨论外形影响时，建立3种模型：实际有桩靴平台模型、无桩靴仅有存放桩靴的桩孔平台模型、既无桩靴也无存放桩靴的桩孔平台模型，分别模拟在不同水深与航速下的流场流动，进而分析阻力系数和抽吸力系数的变化规律。

1 数学模型与控制方程

海上风电作业平台的自航可以近似处理为在静止水域中以稳定的低速航行，其求解问题可转换为海上风电作业平台静止不动，水流均匀流向平台。流体不可压缩且流动定常，忽略重力的作用，考虑流体黏性，该平台的航行速度小于5 kn，兴波阻力较小，忽略自由面的影响。

控制方程包括质量守恒和动量守恒方程。

(1)

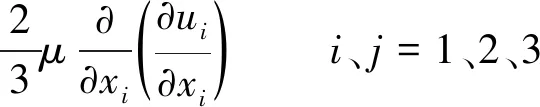
(2)

式中：xi、xj为i、j方向的坐标值；ρ为海水的密度；μ为流体动力黏性系数；ui、uj为速度u在i、j方向的分量；p为压力；Fi为质量力。

采用雷诺平均法(RANS)进行数值模拟，求解不同水深、模型、航速下的流场。采用SSTk-ω湍流模型封闭方程，考虑了横向耗散，涡黏性考虑了湍流剪切应力的输运过程[8]。

2 数值模拟

2.1 计算模型

研究对象为一座近海自升式海上风电作业平台，配置有4条圆筒形桩腿，每条桩腿安装对应的桩靴。平台主尺度参数见表1。

表1 平台主尺度参数

计算模型除了带桩靴的原型平台之外，为了讨论桩靴、桩孔对自升式海上风电作业平台水动力的影响，还构造另外2个模型，见图1。

图1 3种数值计算模型

为展示平台底部的桩靴，图中几何模型为从底面斜向上看的视角，全文图示的艏艉方向：左侧为平台艉部，右侧为平台艏部。桩孔的上部被桩腿几乎完全充满，因此，模型以实体填充；而存放桩靴的桩孔下部，仍有较大空隙，因此，在模型中体现出来。这样桩孔在平台底部可见，见图1a)和图1b)。平台模型以实型尺度建立，且只构建水面以下部分。

为研究浅水效应的影响，计算模型包括水底，见图2。图2中h为水深，T为吃水。

图2 平台吃水T与水深h示意

2.2 计算域与网格划分

由于计算域为浅水，且海上风电作业平台为偏方体结构，导致平台对周围流场影响的范围较大，因此,计算域比一般船舶流场计算要求更大：从艏部向上游延伸1.5倍水线长，艉部向下游延伸3倍水线长，舷侧各取1.5倍水线长。

网格划分采用混合网格，平台表面附近的流动变化剧烈，对平台表面网格进行加密，其中第一层网格间距根据y+值确定(y+值为50～300)；距平台较远的流场，流动变化缓慢，为了减少网格数量，提高计算效率，采用结构网格进行划分，且网格尺度从平台表面按照一定的增长率向外增长，网格变稀。某水深时的计算域与网格划分示意于图3。

图3 计算域与网格划分示意

2.3 边界条件

计算域的边界需要设置边界条件。入口采用速度入口，入口速度取海上风电作业平台实际自航速度；出口采用压力出口，其压力分布设置为参考压强；顶面与侧面设置为对称面；其他边界面，包括平台表面和水底，设置为壁面。

3 浅水效应影响的数值计算

3.1 计算工况

计算模型为实际平台，即图1a)所示的有桩靴模型。水深工况从浅水至深水共取7种，水深吃水比(相对水深)h/T分别为2、3、4、5、7、10、15，吃水保持不变。该平台设计航速为5 kn，速度工况取3、4、5 kn。

3.2 数值计算结果与分析

3.2.1 阻力系数和抽吸力系数表达式

计算结果采用无量纲系数的形式给出，包括阻力系数和抽吸力系数。

阻力系数Cd表达式为

(3)

抽吸力系数Ca表达式为

(4)

式中：Fd为平台所受的阻力；Fa为平台所受的抽吸力；v为入口水流速度；ρ为海水的密度，ρ=1 025.5 kg/m3；S为实际平台的湿表面积，S=4 118.148 m2。

3.2.2 水深对阻力系数的影响

不同相对水深h/T与水流速度v下的阻力系数Cd变化见图4。

图4 相对水深h/T对阻力系数Cd的影响

分析图4，可以得出：

1)相同速度下，随着h/T的增加，水深h增加，平台的阻力系数迅速减小。

2)当h/T≤7时，随着h/T的增加，水深h增加，阻力系数迅速减小，平台在该相对水深时，阻力系数比深水(h/T>7)时大，自航速度会相应减慢，而在迁航时应适当增大拖轮的拖航力。

3)当h/T>7时，阻力系数减小变缓慢，说明此时可以忽略浅水效应对阻力的影响。

4)对应于航速3、4、5 kn，h/T=2的阻力系数相比h/T=15的增幅分别为35.2%、34.9%、31.2%，说明浅水效应对阻力的影响显著。

5)流速3、4、5 kn时，3条阻力系数曲线几乎重合，说明此范围的平台移位速度对阻力系数的影响很小。

3.2.3 水深对抽吸力系数的影响

当平台在浅水中移位时，平台底部与水底之间的流速增加，压强减少，平台底面较低的压强使平台承受一个向下的抽吸力。

不同相对水深h/T与水流速度v下的抽吸力系数Ca变化见图5。

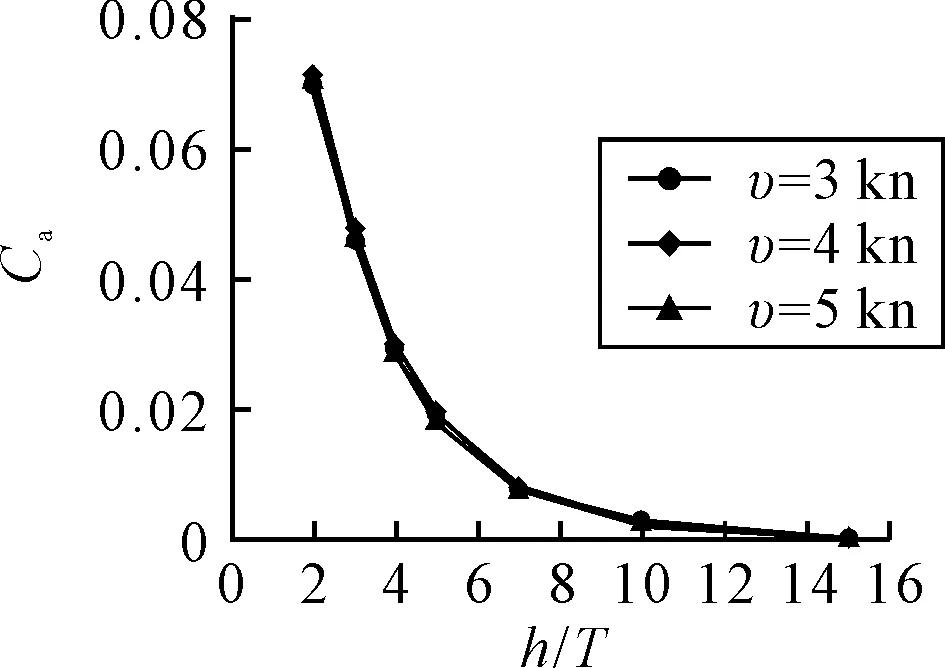
图5 相对水深h/T对抽吸力系数Ca的影响

分析图5，可以得出：

1)相同速度下，随着h/T的增加，水深h增加，平台的抽吸力系数减小。

2)当h/T≤7时，随着h/T的增加，水深h增加，抽吸力系数迅速减小，平台在该相对水深迁航或移位时，抽吸力系数较大，下蹲作用较为明显，应注意平台下蹲引起的平台吃水减小问题，避免储备干舷过小对平台航行安全性产生影响。

3)当h/T>7时，抽吸力系数减小相当缓慢；随着h/T继续增大，h/T>10时，抽吸力系数趋近于0。说明当该平台的航行水深h大于10倍吃水T时，可以忽略浅水效应对抽吸力的影响。

4)流速3、4、5 kn时，3条抽吸力系数曲线几乎重合，说明此范围的平台移位速度对抽吸力系数的影响很小。

5)比较图4与图5，可见平台阻力系数与抽吸力系数的变化趋势相似，并与文献[4]中的结论相一致。

3.2.4 流动细节压强分布云图显示

平台阻力与抽吸力中的形状阻力部分是由对平台表面压强积分得到的。文中仅给出了平台中纵剖面在不同h/T下的压强分布云图，足以显示平台周围，尤其是平台表面压强的分布情况，并能直观地显示出压强分布在不同相对水深h/T时的变化。当速度为3 kn时，在不同h/T下的平台中纵剖面压强分布见图6。

图6 自航速度3 kn时不同h/T下的中纵剖面压强分布

分析图6，由于平台较为丰满，且水具有黏性，水质点沿平台表面的动能逐渐减小，边界层将会在平台某个位置处发生分离，导致漩涡的产生，漩涡处的水压力下降，从而改变了沿平台表面的压力分布情况。在中纵剖面压强图中易发现，h/T越小，水深越浅时，平台艏部的正压强越大，艉部的负压强也越大，这种压强差产生的黏压阻力[9]也越大。

一般情况下，h/T越小，水深越浅时，平台底部与底面边界之间形成的水道越狭窄，流速增加更快，压强更小，分析中纵剖面压强图可见，水深越浅时，平台底部的负压强越大，且负压区也相应增大，导致抽吸力也相应增加。

4 桩靴影响的数值计算

4.1 计算工况

讨论桩靴对平台水动力的影响，设计图1中的3种平台模型进行流动数值模拟。相对水深h/T仍取2、3、4、5、7、10、15。

4.2 桩靴对水动力系数的影响

3种平台模型在航速为3 kn时的阻力系数和抽吸力系数随相对水深h/T的变化见图7。

图7 桩靴对阻力系数Cd与抽吸力系数Ca的影响

分析图7，可得出：

1)桩靴与桩孔对平台阻力系数的影响相当大。①3种模型阻力系数排序为：无桩孔模型<有桩靴模型<仅有桩孔模型；②在h/T=2时，有桩靴模型的阻力系数比无桩孔模型大84.9%，仅有桩孔的阻力系数比有桩靴模型大64.5%；③在h/T=15时，有桩靴模型的阻力系数比无桩孔模型大86.3%，仅有桩孔模型的阻力系数比有桩靴模型大60.7%。

为提升平台的自航速度或提高平台的迁航效率，应综合考虑桩靴的几何形状，或者对桩孔处进行加盖，能显著减小平台所受的阻力。

2)桩靴与桩孔对平台抽吸力系数的影响很小。①3种模型在不同相对水深h/T下的抽吸力系数曲线十分吻合；②有桩靴模型与无桩孔模型的抽吸力系数曲线几乎重合；③仅有桩孔模型在h/T>7时也与其他两个模型的抽吸力系数几乎相同，而在h/T<7时略小于其他两个模型。

4.3 桩靴对速度矢量场的影响

流场速度矢量图能够直观地将流场速度的大小和方向可视化，从而有助于分析桩靴、桩孔对平台绕流流动和阻力的影响。

关于工况，速度取较高的v=5 kn，因为其流场变化更加明显，取水深最大的情况，相对水深为h/T=15，此时可以忽略水深的影响。

桩靴和桩孔对流动的影响在平台底面附近更加明显，所以截取流场在平台底处的截面，在此截面上显示其速度矢量分布，见图8。图8中箭头的长度和方向分别代表速度的大小和方向。

图8 3种模型在平台底截面处的速度矢量分布

分析图8可以发现，桩靴与桩孔对平台流场以及阻力的主要影响如下。

1)桩靴与桩孔处的流场。在桩孔与桩靴的开口区域存在着涡流，明显可以看出仅有桩孔模型的涡流比有桩靴模型的涡流更严重，增加了艏部与桩靴、桩孔之间的压力差值，从而增加了黏压阻力。

2)平台艉流场。桩靴和桩孔附近的外形曲率大，加速了平台底面的边界层分离，极大干扰了艉流场，有桩靴模型与仅有桩孔模型的艉流场存在大量涡流，且仅有桩孔模型的涡流比有桩靴模型的涡流更严重，而无桩孔模型艉流场的水流则更为规则，艉流场的涡流增加了艏部与艉部之间的压力梯度，从而增加了黏压阻力。