电驱动差速转向轮式水陆两栖车辆可收放悬架机构运动学分析与参数优化

剧冬梅， 项昌乐， 陶溢， 徐小军， 王文浩

(1.北京理工大学 机械与车辆学院， 北京 100081； 2.中国兵器科学研究院， 北京 100089； 3.北京特种车辆研究所， 北京 100072； 4.国防科技大学 智能科学学院, 湖南 长沙 410073)

0 引言

水陆两栖装备对海上运输、海洋开发和军事活动具有重要意义，其重要的应用价值使得20世纪以来许多国家开展了相关研究。20世纪70年代后，主要军事强国的陆军轻型战斗车辆基本实现了两栖化[1]。近些年，随着世界格局的稳定，两栖车辆技术开始逐渐向民用领域拓展，主要应用于抢险救灾和极限运动[2]。目前典型两栖车辆有美军EFV履带式两栖突击车、俄罗斯BTR-80和BTR-90系列轮式两栖步兵战车、俄罗斯“野牛”气垫船、英国Aquada轮式两栖车等[3-4]。

限制水陆两栖装备水面速度的一大因素就是车体航行阻力[5]。两栖装备水中行驶时，车轮部分将产生大量涡流损失，所产生的阻力约占总阻力的25%. 为减少水陆车辆在水中的行驶阻力，需针对水陆两栖装备设计一种可收放悬架系统，在陆上行驶时，这种可收放悬架系统发挥普通悬架的作用，传递作用在行走机构与车体间的力和力矩，缓和车辆行驶时传到车体的冲击力，并减少车体振动。当两栖车进入水中时，可收放悬架系统又能将行走机构整体收起，通过减少行走机构的涡流损失以实现减阻增速，提高其推进效率。

英国Gibbs公司的高速两栖汽车(HSA)采用了一种可收放悬架，该车陆上时速达160 km/h，水上行驶时通过收放悬架将车轮收起，航速可达55 km/h[6]，其收放悬架结构已申请了相关专利[7]；该可收放悬架结构复杂、占用空间较大，目前只应用于轻型民用车辆，尚未应用在军事领域。美国于1997年也设计了一种可收放悬架[8]，该收放悬架类似于双横臂悬架，结构简单，车轮在提升过程中翻转角很小，但其收放行程较小，减阻增速效果不明显。

本文提出了一种新的可收放悬架，并以提高悬架运动特性和收放特性为目标，对行走机构的收放高度、翻转角度、外倾角以及主销内倾角等关键参数进行优化设计。

1 可收放悬架方案

本文提出的一种轮式两栖车辆行走机构采用4个轮式行走机构，每个轮式行走机构均安装了一个轮毂电机，车辆通过差速实现转向，因此收放悬架不涉及车轮驱动机构和转向机构。

两栖车辆悬架系统应该尽量简单可靠，能够保证装备越野行驶时有效地缓和来自颠簸地面的振动[9]，水上航行时能够平稳而迅速地将行走机构完全收起，实现减阻增速。针对现有可收放悬架的不足，将减振效果良好且振动过程中能保持行走机构外倾角变化较小的双叉骨式悬架与旋转驱动收放的四连杆机构相结合，设计出一种新型可收放悬架。图1为采用新型可收放悬架方案的某水陆两栖车前后视角简图，车辆前后、左右对称布置4个相同的可收放悬架。悬架上横臂两端分别与车体和叉骨连杆连接，叉骨连杆与行走机构铰接，下横臂一端与行走机构固连，减振器一端铰接于下横臂。另有一主动摇臂，起始端与车体铰接，末端与减振器相连，主动摇臂上方有一与车体固连的限位块，对摇臂进行限位。主动臂、减振器、下横臂与车体构成另一个四连杆结构。

图1 水陆两栖车可收放悬架方案Fig.1 Front and rear views of retractable suspension schemes of amphibious vehicle

在陆地行驶时，限位块限制主动臂向上转动，与主动臂连接的减振器上端则可视为与车体铰接。此时收放悬架发挥普通悬架的减振作用。当两栖车完全驶入水中时，主动臂向地面一侧转动，而减振器发挥连杆作用，当越过极位后带动下横臂向车体上方转动，实现行走机构的翻转和提升。本文悬架的优点在于采用了经典四连杆机构加限位的方法，可同时实现行走机构的提升与翻转，结构简单可靠，减振器在陆上行进发挥减振作用，在收放过程中充当连杆，实现了构件的一体多用。此外，收放机构采用了旋转驱动，相比直线驱动节约了竖直方向上的空间。

2 运动学分析

图2为车辆右后侧可收放悬架结构简图，其中：A为主动臂与车体的铰链点，B为主动臂与减振器的铰链点，C为下横臂与行走机构的固连点，D为下横臂与车体的铰链点，E为叉骨连杆与上横臂的铰链点，F为上横臂与车体的铰链点，G为行走机构中心，l1、l2、l3、l4、l5、l6分别表示车体上铰链点A与铰链点D间的距离、主动臂长度、减振器长度、下横臂长度、叉骨连杆长度和上横臂长度，l7表示铰链点F与铰链点D之间的距离；θ1表示铰链点A与铰链点D的连线AD与x轴的夹角，θ2表示主动臂与x轴的夹角，θ3表示减振器与x轴的夹角，θ4表示下横臂与x轴的夹角，θ5表示叉骨连杆与x轴的夹角，θ6表示上横臂与x轴的夹角。减振器、下横臂和叉骨连杆并未铰接于同一点，且行走机构与叉骨连杆固连时，构成典型双叉骨式悬架。

图2 右后侧可收放悬架结构简图Fig.2 Schematic diagram of right rear retractable suspension

按图2所示结构建立坐标系，在坐标系中将构件用矢量表示，并采用闭环矢量法建立机构的位置方程，则有

l1+l4=l2+l3.

(1)

设定各杆件及主动臂转角θ2已知，θ1为常量。将(1)式分别在x轴和y轴方向投影后，有

(2)

以下横臂的运动为已知运动，再一次采用闭环矢量法可以研究下横臂、叉骨连杆、上横臂及车身部分组成的四连杆中各部件的运动情况：

l4+l7=l5+l6.

(3)

车身部分长度l7及其与水平方向的夹角θ7已知。从(2)式、(3)式可以看出，通过行走机构在提升过程中，其质心的横坐标、纵坐标以及其相对于车身的旋转角度3个参量就可以完全表征该行走机构的运动。由于叉骨连杆和行走机构固连，为了由叉骨连杆的运动参数直接得到行走机构的参数，需要进一步分析。

图3为收放过程中行走机构的运动示意图，其中：ΔyG和ΔθG分别表示行走机构中心G的纵坐标的变化量和相对初始位置的旋转角度，即行走机构在收放过程中的提升高度和翻转角度；Δθ5表示叉骨连杆相对自身的旋转角度。

图3 收放过程中行走机构运动示意图Fig.3 Schematic diagram of travelling mechanism during retracting

根据平面运动学规律可知：

ΔθG=Δθ5.

(4)

进一步根据矢量旋转方程：

(5)

式中：

(6)

则

DG′=DC′+C′G′.

(7)

(5)式分别展开，有

(8)

(9)

式中：xD、xC、xC′、xG分别表示D、C、C′、G点的横坐标；yD、yC、yC′、yG分别表示D、C、C′、G点的纵坐标。

(8)式和(9)式扩充维数，可进一步得到

(10)

(11)

(4)式、(10)式和(11)式即为能够完整表征行走机构在收放过程中运动状态的3个参量。

3 悬架参数优化

可收放悬架存在两种工作状态，即陆地行进时伴随崎岖地面起伏悬架的上下跳动，以及进入水中时对行走机构的收放过程[10]。因此，对于可收放悬架的优化，需要在保证对行走机构实现最大程度收放的同时，还要使悬架在陆地行驶时具有合理的运动学特性，因此需分别针对可收放悬架的收放和陆地行驶两种工况进行参数优化，悬架水中收放以行走机构收放高度和翻转角度为优化目标，陆地行驶性能以行走机构外倾角和主销内倾角为优化目标。

3.1 总体优化策略

图4 可收放悬架优化策略Fig.4 Optimization strategy of retractable suspension

可收放悬架的水中收放与陆地减振行驶是两个联系的运动过程，对其中一个运动过程的优化会造成机构参数的变化，势必会影响另一个过程的运动性能。因此，本文将其中一个运动过程的目标函数作为另一个运动过程优化的限制条件，并考虑到可收放悬架系统的参数化表达式中包含大量三角函数，无法直接解出明确的目标函数和限制函数等情况，采用多体动力学软件ADAMS/Insight模块有效地区分关键参数和非关键参数，观察参数对系统的性能影响，从而在实物样机制造前，可以综合考虑各种参数以获得最优的设计参数。图4为针对可收放悬架系统水中收放和陆地行进两个过程的优化策略。

3.2 虚拟实验设计与优化变量选取

考虑到悬架运动学特性参数的绝对数值相对较小，且对于系统参数的变化较为敏感，实现优化的难度较小，因此首先分别对陆地行驶过程和水上行走收放过程进行实验设计，并完成灵敏度分析。然后根据变量参数对两个过程指标参数的灵敏度不同，选择对收放过程具有高灵敏度且对陆地行驶运动参数灵敏度较低的参数；对收放过程进行优化，采用对收放过程具有低灵敏度且对陆地行驶运动参数灵敏度较高的参数对悬架运动学特性参数进行优化。最后通过对两个优化结果进行综合分析并反复优化，确定最终的系统参数。

对于收放过程，由于可收放悬架系统参数取值变化对收放运动效果影响力有所不同，为判断每个变量对目标的影响程度，进而在机构优化设计中依据影响度大小来选择优化设计变量，需要对收放过程中的系统参数对目标影响度进行灵敏度分析。可收放悬架有8个关键设计点，每个设计点有x轴、y轴、z轴方向各3个坐标参数，如果对所有参数均做优化研究，则有24个变量。根据可收放悬架的工作原理，将各构件简化为平面内的部件，如图5所示。进一步固定D点位置，并作为坐标系原点。同时假设下横臂在设计位置保持水平，因此减振器与下横臂铰链点C2、叉骨连杆与行走机构铰链点C1的坐标参数只需以x轴坐标作为变量。由于叉骨连杆在整个过程中均与行走机构保持相对固定，行走机构的提升、翻转以及定位参数均取决于E点和C1，而和减振器与下横臂铰链点C2无关，因此，实际作为可收放悬架参数灵敏度分析的变量如表1所示。

图5 可收放悬架系统优化原理图Fig.5 Schematic diagram of optimized retractable suspension

在设计实验过程中，通过筛选研究可以分析每个变量对设计目标的贡献，将实验缩小到重要因素，并确保不排除重大因素或影响，即对各个设计变量进行灵敏度分析。由于设计变量较多，在对灵敏度进行分析时，采用线性Fractional Factorial设计类型，针对收放过程行走机构的提升高度共进行16次仿真实验，分析结果如表2所示。

表1 灵敏度分析变量

表2 收放过程提升高度灵敏度分析结果

采取同样的实验设计方法，针对收放过程行走机构的翻转角度共进行16次仿真实验，结果如表3所示。

通过分析行走机构收放高度和翻转角度的实验设计结果可知：对两个目标均具有较大灵敏度的设计变量有DV_4、DV_6、DV_5、DV_1、DV_10、DV_9；对于两个目标均具有较小灵敏度的设计变量有DV_3、DV_2、DV_7. 由于对水陆两栖车行走机构的收放中，提升高度的重要性高于翻转角度，经过综合考量，选取DV_4、DV_6、DV_10、DV_5、DV_1作为收放过程优化变量；选取DV_3、DV_2、DV_7作为悬架运动学特性优化变量。

表3 收放过程翻转角度灵敏度分析结果

3.3 收放指标优化

收放悬架能够正确实现对行走机构的收放，需要满足：

(12)

同时，当收放过程达到四杆机构ABCD的极位，即A、B、C处于同一直线时，机构需要满足：

(13)

xC1>xC.

(14)

将(1)式和(3)式联立，作为收放过程优化的限制条件。由3.2节可收放悬架收放过程设计变量灵敏度的分析结果，选取DV_4、DV_6、DV_10、DV_5、DV_1作为收放过程优化变量。以行走机构质心G点的y轴坐标最大值为优化目标，经过多次迭代得到优化后的设计变量值如表4所示。

表4 优化设计变量值

优化前和多次迭代后最优化的结果导入MATLAB软件进行比较，优化前后行走机构的提升高度和翻转角度对比如图6和图7所示。

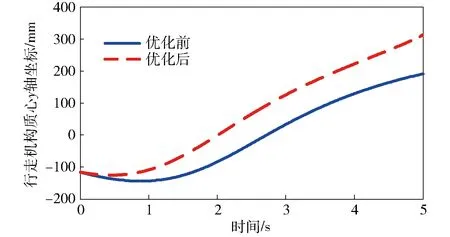
图6 行走机构提升高度优化Fig.6 Height optimization of travelling mechanism

图7 行走机构翻转角度优化Fig.7 Flip angle optimization of travelling mechanism

由图7中优化前后行走机构提升高度的变化曲线可知：优化后提升高度最大值有显著增加，增加了64.8%. 同时优化后提升速率也得到了增加，即要求提升同样高度情况下，优化后的系统所需时间更短。行走机构提升前的下放过程中，其下放的最大值在优化后降低了12.9%，即优化后的可收放悬架在对行走机构提升时，初始阶段先向下推动的动作幅度得到了减小，符合预期结果。由图7行走机构翻转角度变化曲线可知：优化后翻转角度最大值也有明显提升，增加了112.2%；但翻转角度初始值不再是0°，而是-1.56°，需要在行走机构的定位参数优化中做进一步的优化。

3.4 悬架典型运动学特性优化

车轮上下跳动时，悬架运动学特性变化反映了悬架性能。在正常车轮跳动行程内，应使车轮运动特性参数变化量保持在合理范围内，以保证车辆具有设计所期望的行驶特性[11]。基于上述可收放悬架系统参数优化策略、灵敏度分析以及收放过程优化结果，对悬架运动学特性进行优化。

行走机构定位参数中外倾角γ、主销内倾角σ以及轮距L的计算公式为

(15)

L=2xG.

(16)

在ADAMS软件模型基础上构建实验台，同时建立(15)式和(16)式中的外倾角、主销内倾角、轮距3个测量，然后选取DV_2、DV_3、DV_7、DV_9作为悬架运动学特性优化变量，以最小化主销内倾角最大值为优化目标，在[-50 mm,50 mm]车轮跳动行程范围实验下经过多次迭代，得到优化后的变量如表5所示。

表5 定位参数优化前后变量对比

优化前后测得的主销内倾角、优化前后的车轮外倾角以及优化前后的轮距分别进行对比，结果如图8和图9所示。

图8 主销内倾角优化前后对比Fig.8 Kingpin inclination angles before and after optimization

图9 车轮外倾角优化前后对比Fig.9 Wheel cambers before and after optimization

由优化结果来看，主销内倾角在[-50 mm,50 mm]车轮跳动行程范围实验下最大值、最小值均减小了0.75°，相应的车轮外倾角则整体增加了1°左右，同时平衡位置的外倾角由原来的近似0°增加到了1°，这对于将平台满载时其车轮外倾角减小至0°，并减小行走机构的不正常磨损是有益的。因此表明本文所设计的优化方案针对行走机构定位参数的优化是有效的。

4 结论

本文提出了可降低水陆两栖车辆的水中形状阻力、提高水中行驶速度的可收放悬架方案，对该悬架运动特性进行了分析与优化。得到以下主要结论：

1) 通过运动学分析得到描述悬架机构运动特性的公式，从而能够完整表征行走机构在收放过程中运动状态的3个参量。

2) 设计ADAMS/Insight软件模块仿真实验实现了收放悬架的优化，优化实验结果证明所选取的优化变量有效，悬架参数优化后行走机构收放高度和翻转角度显著提高。

3) 参数优化后，陆地行驶时行走机构的主销内倾角和外倾角变化更加合理。