聚能射流对厚壁移动靶的侵彻理论与数值模拟分析

贾鑫， 黄正祥， 徐梦雯， 肖强强

(南京理工大学 机械工程学院, 江苏 南京 210094)

0 引言

近程末端反导是防护己方目标免受导弹袭击的最后一道屏障。如何有效地打击并摧毁来袭导弹，达到一击毙命的效果，一直是国内外学者们研究的热点。目前，各国采取的反导措施主要是以定向战斗部、可控离散杆战斗部、聚焦战斗部等高速破片毁伤元的拦截形式为主，利用动能毁伤元对导弹关键部位侵彻，使导弹偏离其预定轨道或直接侵彻并引爆战斗部，从而达到反导的目的，其中以直接引爆战斗部效果最佳[1-2]。随着深侵彻导弹战斗部的壳体厚度不断增加，传统依靠破片式或动能杆式战斗部产生的毁伤元已无法对付大着速(着速大于500 m/s)、大壁厚(壁厚大于100 mm)、高强度壳体的战斗部，对己方战略要地的防护形成了严峻挑战[3-4]。

另外一种具有超强毁伤能力的毁伤元是聚能射流。聚能射流因其具有较高的侵彻能力，广泛应用于军事和民用领域中。射流侵彻静态靶板方面的研究成果非常多，具有比较成熟的理论基础[5-8]。关于聚能射流侵彻运动靶板的机理，大多研究是基于爆炸反应装甲与射流的相互作用而开展的[9-12]。爆炸反应装甲的特点是面板和背板通常仅有几毫米，射流在侵彻这种薄运动靶时一般是忽略射流速度的衰减以及射流的断裂和偏移等影响。Yadav[13]、Jia等[14]、Mayseless等[15]、Luttwak等[16]均对这一现象做了详细描述。

对于射流侵彻高速厚壁移动靶侵彻机理研究的学者较少。目前，Marmor等[17]利用240 mm 滑膛炮作为移动靶的发射装置，采用80 mm聚能装药进行了射流侵彻移动靶动态试验，并通过较简单的工程模型进行了验证。该模型假设聚能射流的头尾速度呈线性变化，仅适用于单锥罩这种简单的药型罩结构，且模型中并没有考虑射流头部至尾部速度的非均匀分布、射流横向干扰速度、靶板阻抗等因素。国内也有少许研究人员采用仿真模拟手段进行了一些初步研究[18-19]。总之，现有工程计算模型都无法满足射流侵彻大壁厚移动靶的精确计算。

本文基于虚拟源点理论并采用微元法，将射流微元与移动靶板的相互作用过程分为两个阶段，通过对侵彻过程进行动态分析，基于伯努利方程和Held扩孔方程建立了射流侵彻厚壁移动靶的理论模型等。得到了射流侵彻移动靶的开孔和侵彻深度计算方法，并通过仿真计算和Marmor等[17]的试验结果对理论模型进行验证。

1 理论分析

1.1 静破甲过程分析

聚能射流存在一定速度梯度，头部速度快，尾部速度慢，随着侵彻的进行，射流会被不断拉伸。假设存在一个虚拟源点，虚拟源点是所有射流发出的源点，在运动过程中射流微元速度不发生变化[20]。根据这一假设，当射流着靶时刻为t0时，将已经拉伸至靶板表面且具有侵彻能力的射流，即微元运动速度vj大于射流临界侵彻运动速度vj，min划分为n段微元，每段微元近似为圆柱体，并且任一微元在运动过程中速度不发生变化[21]。在t0时刻，第i段微元与靶板表面距离及其速度、长度、半径和该微元头尾速度差分别为Lj，i、vj，i、lj，i、rj，i和Δvj，i，其中Δvj，i=vj，i-vj，i-1，即前一段射流微元与后一段射流微元速度差。假设第i段微元到达孔底时射流侵彻深度为Pi-1，则该微元到达孔底经历的时间ta，i即为前面i-1段微元侵彻所用时间tc，i-1，假设到达时间为tz，i，二者间有如下关系：

(1)

假设射流在拉伸过程中体积不变，第i段微元断裂时刻为tb，i，断裂后微元的速度、长度与直径等与断裂前一刻均相同，忽略断裂射流的翻转、偏离及重新开坑时的能量消耗。

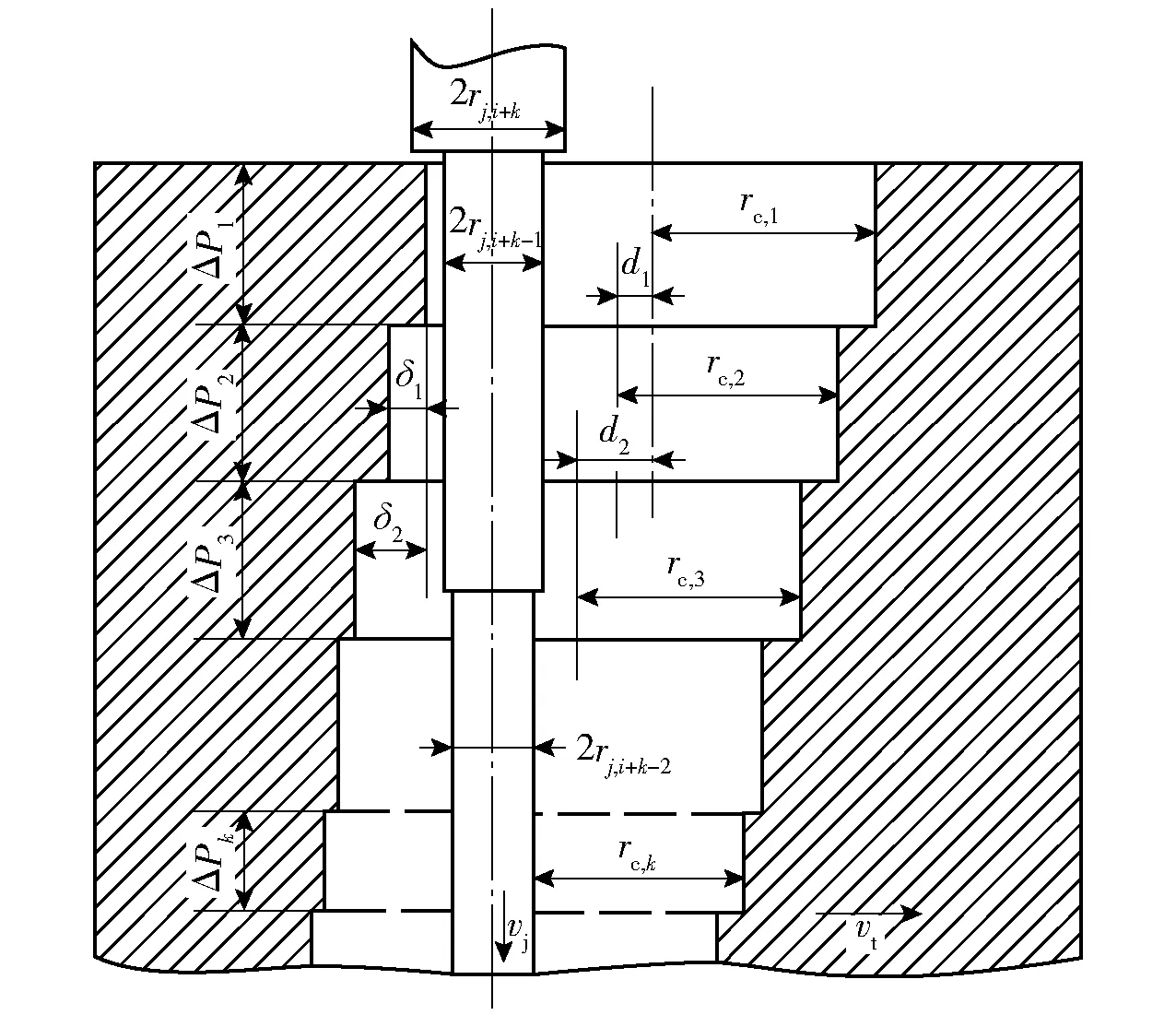
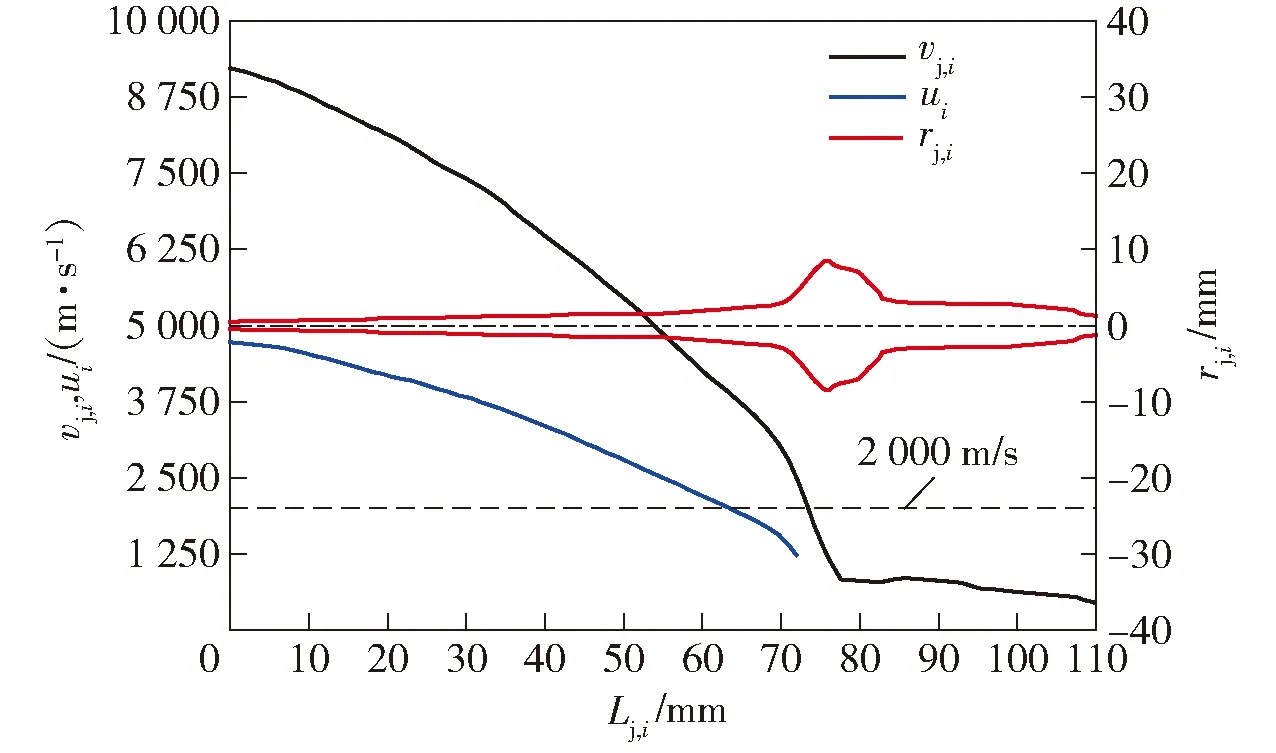
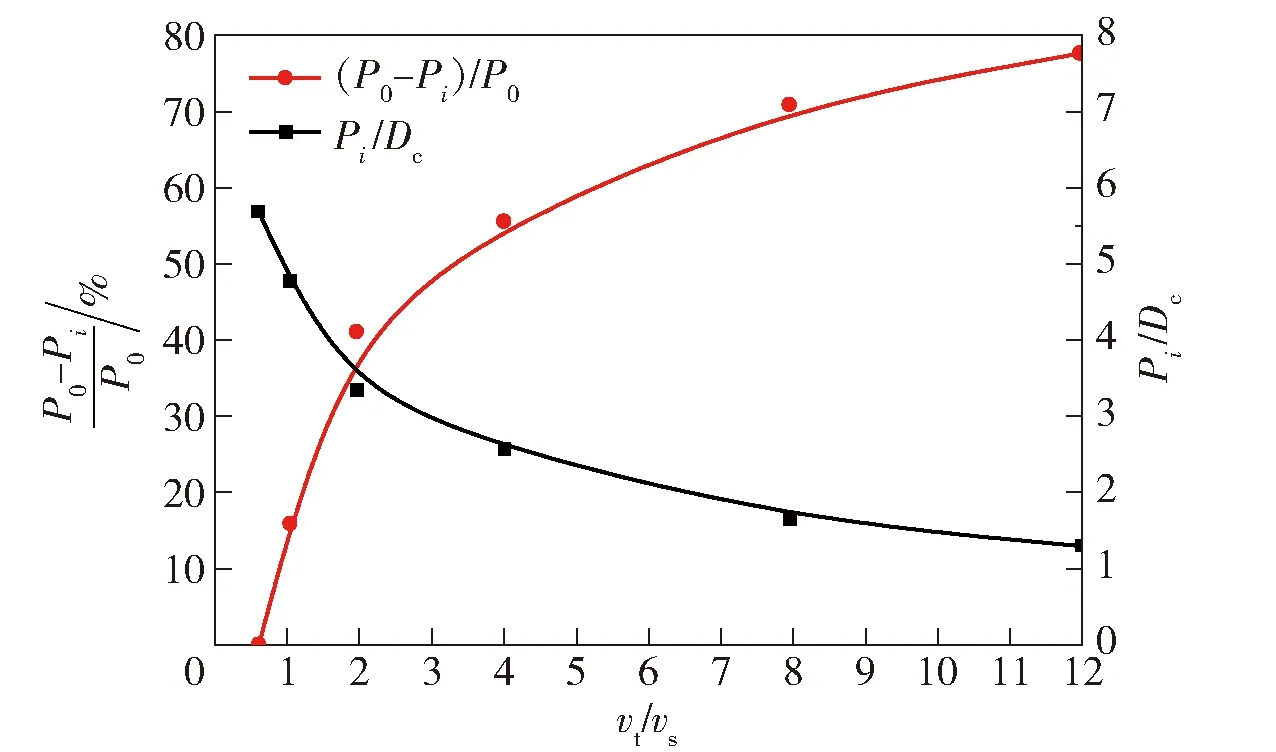
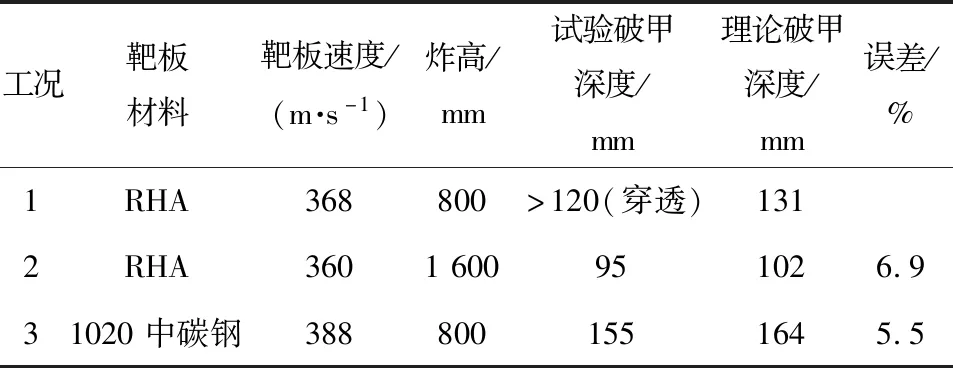
若第i段微元到达孔底的时刻tz，i

(2)

若第i段微元达到孔底的时刻tz，i>tb，i，则该微元在着靶前已经发生断裂，断裂后微元长度l′j，i与直径r′j，i即为射流微元着靶时的参数，分别为

(3)

假设射流对靶板的侵彻过程为碰撞点上靶板材料以侵彻速度运动的过程，微元在碰撞过程中速度、直径不再发生变化。由于射流微元运动速度大于侵彻速度，微元会因为速度差被损耗销蚀，其侵彻时间即为该段微元被销蚀的时间。假设第i段微元的侵彻速度为ui，则该微元在侵彻过程中的侵彻时间Δtc，i和侵彻深度ΔPi的关系如下：

(4)

ΔPi=uiΔtc，i，

(5)

则第i段射流微元侵彻结束时，射流侵彻深度Pi与侵彻时间tc，i为

Pi=ΔP1+ΔP2+…+ΔPi，

(6)

tc，i=Δtc，1+Δtc，2+…+Δtc，i.

(7)

1.2 轴向侵彻速度分析

由于射流具有很高的速度，撞击靶板时超过了靶板声速，碰撞点处会产生冲击波，且冲击波会同时传入靶板和射流中。由于射流直径较细，受径向稀疏波的吸收较强烈，使得冲击波在射流中传播距离很短，对聚能射流侵彻靶板过程的影响有限，因此可不考虑射流中冲击波的作用。对于钢靶而言，由于密度和声速比较高，聚能射流的侵彻速度和靶板材料的声速相比并不算高，因此不考虑可压缩性对侵彻过程的影响[22]。

假设第i段微元的侵彻速度为ui，若射流强度取Yj=0、靶板强度为Rt、射流侵彻过程满足伯努利方程，则修正后的伯努利方程为

(8)

式中：ρj和ρt分别为射流密度和靶板密度。当ρj=ρt=ρ时，第i段微元在靶板中的侵彻速度为

(9)

当ρj≠ρt时，第i段微元在靶板中的侵彻速度为

(10)

第i段微元侵彻速度代入(4)式和(5)式中，即可算得该微元的侵彻深度ΔPi.

1.3 射流侵彻移动靶孔径分析

Szendrei[23]认为，孔径增长过程为孔壁压力克服靶板阻力使得孔径增加的过程，并假设径向孔径增长的初始速度等于射流的轴向侵彻速度。Held[24]在Szendrei[23]的基础上对其扩孔公式进行了改进，并认为靶板强度对射流的扩孔速度与半径影响较大。在射流微元侵彻靶板过程中，当靶板与射流微元发生接触碰撞时，射流除了要克服靶板强度Rt，还要克服因靶板以速度vt运动产生的动压pt，

(11)

根据伯努利方程，第i段微元对应的孔壁处的压力为

(12)

式中：uc，i为第i段射流微元与孔壁作用时孔径的增长速度。假设射流微元轴向侵彻时间与径向扩孔作用时间相同，则径向扩孔速度表达式为

(13)

rc,i为第i段射流侵彻孔径的半径。

Szendrei[23]假设侵彻过程中，靶板孔壁处的压力与开孔面积的乘积保持为常数。靶板开孔初始孔径即为射流直径，因此孔壁压力变化与初始孔壁压力间的关系满足下式：

(14)

式中：r′j，i为第i段射流与靶板孔底或孔壁相碰撞时的半径；p0，i为第i段射流微元撞击靶板的初始压力，可以表示为

(15)

ui可用(9)式或(10)式计算得到。(15)式代入(14)式，可得到孔壁压力随孔径变化的公式：

(16)

(16)式代入(13)式中，可得到径向扩孔速度随孔径变化的公式：

(17)

式中：

(18)

对(17)式进行积分，得到射流扩孔半径rc，i与侵彻作用时间tc，i的关系为

(19)

当径向扩孔速度uc，i降低至0时，侵彻孔径达到最大值ri，max，由(17)式可以计算得到最大侵彻孔径半径为

(20)

与Szendrei[23]和Held[24]的方程相比，(17)式、(19)式、(20)式中加入了靶板运动速度vt，且靶板运动速度越大，侵彻孔径能达到的最大孔径越小。当靶板移动速度vt为0时，上式转变为Szendrei[23]和Held[24]的扩孔方程。

假设靶板孔壁与第i段射流微元的作用面积为射流微元轴向截面积，侵彻过程中射流微元半径与长度分别为r′j，i和l′j，i，则作用面积Si[14]为

Si=2l′j，ir′j，i，

(21)

根据侧向力Fi与压力pi的关系，得到

Fi=2pil′j，ir′j，i.

(22)

1.4 受干扰时刻分析

侵彻初始阶段，视能够到达孔底的射流微元侵彻过程与静侵彻相同。由于靶板移动量累积，孔壁面与射流轴线逐渐逼近，后续射流微元会在到达孔底前即与孔壁一侧相碰撞。射流微元单侧在靶板孔壁侧向力作用下具有横向位移，前部分射流若与该微元间连续，则前部分射流也会有横向运动，偏离原侵彻孔中心线。当射流微元与另一侧孔壁相碰撞时，微元对孔壁进行二次侵彻，无法到达孔底，对侵彻深度无贡献。

由(18)式、(20)式可得

(23)

当射流与靶板材料、靶板移动速度确定后，微元对靶板的最大扩孔半径与(vj，i-ui)rj，i呈正比。将(9)式、(10)式分别代入(23)式中，得到

(24)

式中：

(25)

通常在射流侵彻初始阶段，射流侵彻形成的孔径最大，但由于靶板移动，相当于射流以同样大小的速度反方向运动，射流侵彻靶板形成的孔径示意图如图1所示，靶板移动速度向右且垂直于射流轴线，孔径中心线即为对应射流微元侵彻靶板时的轴线。图1中k表示由第k个射流微元侵彻形成的侵彻孔编号。假设第i段和第i+1段射流微元能到达孔底，且侵彻靶板期间靶板与微元间无相对运动，即微元轴线与对应侵彻孔径经过Δtc，i时间后第i段微元侵彻结束。下一射流微元轴线相对于靶板移动的距离为vt×Δtc，i，则第i+1段微元轴线与第i个侵彻孔径中心线间距为Δdi=vt×Δtc，i，第i+1段微元轴线与第1个侵彻孔径中心线间距为di=vt×tc，i. 第i+1个射流微元侵彻形成的孔壁与第1个射流微元侵彻形成的孔壁距离为δi.

图1 无干扰阶段的侵彻孔径Fig.1 Penetration radius without interference

由(1)式可得第i段射流微元到达孔底时刻为t0+ta，i，此时编号为k的微元与靶板初始表面距离为|Lj，k-vj，kta，i|，若

|Lj，k-vj，kta，i|≤l′j，k，

(26)

则表明第i段射流微元到达孔底时，第k段射流微元处于靶板入孔处，由(26)式可以计算得到k值。根据图1可得入孔处射流微元侧表面与孔壁最小距离为

Δk=rc，1-(vtta，i+r′j，k)，

(27)

式中：r′j，k为第k段微元在t0+ta，i时刻的半径。当Δk>0时，在ta，i侵彻时间内孔壁不干扰射流；当Δk<0时，第k段射流微元开始受到靶板孔壁干扰。由于靶板与射流发生干扰后，射流变形与侵彻情况较为复杂，下面结合仿真对射流干扰阶段的侵彻深度规律进行研究。

2 仿真分析

2.1 模型建立

仿真计算所用聚能装药口径为40 mm，药型罩为等壁厚双锥罩，其中小锥角为40°、大锥角为60°，药型罩壁厚为0.7 mm，装药高度为68 mm，带有波形调整器，炸高为80 mm. 图2所示为聚能装药结构示意图。

图2 聚能装药结构示意图Fig.2 Structure of shaped charge

为方便获得射流拉伸至靶板表面时射流的头尾速度、速度梯度、半径和相对位置等理论计算所需的参数，采用数值模拟仿真软件ANSYS/LS-DYNA建立射流侵彻移动靶板的三维模型。利用任意拉格朗日- 欧拉(ALE)流体与固体耦合算法进行数值模拟。数值模拟中涉及到炸药、空气、药型罩、波形调整器和靶板5种材料模型，其中炸药为JH-2炸药，药型罩材料为紫铜，靶板为45号钢，波形调整器为酚醛树脂材料。图3所示为聚能射流侵彻移动厚壁战斗部壳体有限元模型及网格划分情况，其中，炸药、空气、药型罩和波形调整器采用欧拉共节点网格，靶板采用拉格朗日网格。

图3 有限元模型Fig.3 Finite element model

药型罩和靶板材料模型均采用JOHNSON-COOK模型和EOS_GRUNEISEN状态方程描述，炸药材料模型均采用高能炸药爆轰模型和JWL状态方程进行描述。空气域采用NULL 材料模型，状态方程采用 EOS_LINEAR_POLYNOMIAL. 波形调整器采用 MAT_ELASTIC_PLASTIC_HYDRO模型，状态方程采用 EOS_GRUNEISEN. 表1给出了高导无氧铜与45号钢的相关材料参数[12, 25]，表2给出了JH-2炸药材料参数[10]，表3给出了波形调整器材料参数[26]，表3中各参数的含义见参考文献[27]。

表1 高导无氧铜与45号钢材料参数[12,25]

表2 JH-2高能炸药材料参数[10]

表3 波形调整器材料参数[26]

2.2 射流参数及理论静破甲深度分析

根据聚能射流成型的仿真结果，取lj，i=2.5 mm，用取点法得到射流成型时其半径与速度参数，如图4所示。

图4 射流微元速度、半径及侵彻速度与距靶板表面距离关系图Fig.4 Relationship among vj,i, rj,i and ui of jets and Lj,i

根据经验，当射流速度vj>2 000 m/s时，射流具有破甲能力[28]。取有效射流段参数，将每段微元参数代入(10)式中，可以计算得到每段微元对应的侵彻速度，如图4中所示。

根据(5)式、(6)式、(20)式，可计算得到该聚能战斗部的静破甲破甲深度扩孔曲线，如图5所示。理论计算得到该破甲弹在80 mm炸高下最大破甲深度为209 mm，靶板表面开孔直径为9.2 mm，最大扩孔直径为15.3 mm.

图5 破甲深度与扩孔曲线图Fig.5 Penetration depth and radius

2.3 LS-DYNA仿真分析

采用LS-DYNA数值模拟方法，采用图2的聚能装药结构，炸高为80 mm，建立靶板速度vt分别为0 m/s、50 m/s、100 m/s、200 m/s、400 m/s、600 m/s的6个仿真模型并进行计算，仿真结果如图6所示。

图6 LS-DYNA仿真破甲深度结果图Fig.6 Simulated penetration depth of LS-DYNA

仿真设置的炸高较小，静破甲过程中射流基本没有发生断裂，视为连续射流侵彻；动破甲过程中靶板干扰射流前射流也连续，因此该过程也视为连续射流侵彻。当速度分别为50 m/s 和100 m/s时，杵体直接受到靶板横向力的干扰，导致侵彻通道中还未完成侵彻作用的具有破甲能力的射流弯曲、断裂并且与两侧孔壁相互作用，使破甲深度降低；当速度分别为200 m/s、400 m/s和600 m/s时，具有破甲能力的射流直接受到靶板横向力的干扰，射流在横向干扰力作用下发生弯曲和断裂，破甲深度显著降低。

由图6可以看出，随着靶板移动速度的增大，射流受靶板干扰的时间点提前，且射流的破甲深度明显减小，破甲深度分别为5.7Dc、4.775Dc、3.35Dc、2.55Dc、1.65Dc、1.275Dc(Dc为装药直径)。如图7所示拟合出曲线，横坐标以vs=50 m/s作为靶板速度增量的衡量标准，左侧纵坐标为移动靶作用下射流破甲深度的降幅，P0为靶板移动速度为0 m/s时的破甲深度，Pi为不同靶板移动速度下的射流侵彻深度。当vt/vs≤0.6即vt≤30 m/s时，靶板移动对射流侵彻过程无干扰，射流侵彻移动靶板的深度与静侵彻深度时相同。表明靶板在干扰射流微元前，对破甲深度有贡献的射流微元已经作用完毕，后续靶板干扰的射流部分无侵彻能力。右侧纵坐标为破甲深度与弹丸直径的比值。随着靶板移动速度的增加，射流破甲深度的下降幅度呈先快、后趋于平缓趋势。根据理论分析，由于射流头部速度较高，开孔时对靶板有明显的扩孔效应，使得射流前部分微元能在不受干扰下进入侵彻孔中，对靶板进行侵彻。

图7 破甲深度降幅、破甲深度比与靶板速度增量比关系Fig.7 Relationship between penetration depth and target velocity

2.4 理论计算移动靶板破甲深度

通过射流成型仿真结果，取射流头部速度为9 100 m/s、尾部速度为2 000 m/s，这一段射流到达靶板表面时的有效长度约为67 mm，取每段微元的长度为2.5 mm，因此可将具有侵彻能力的射流分为27段微元。从射流头部至尾部依次编号为1～27，根据(26)式、(27)式，可以计算出靶板初始干扰射流时位于孔底的射流微元编号i，此时已经完成侵彻的有效微元占比以及此刻射流侵彻深度。相关数据表4所示。

假设编号i后的有效射流微元均断裂，即编号i后的射流微元以t0+ta，i时刻的几何形状侵彻靶板，用(3)式、(4)式、(5)式可计算断裂后的射流微元侵彻深度，如表5所示。

表4 无干扰阶段的微元及破甲深度

表5为编号i后射流均断裂时的总破甲深度Ptot. 结合表4中的数据发现Pi-1+Ptot/2与仿真破甲深度接近，假设靶板移动时其破甲深度可以用Pi-1+Ptot/2估算，仿真破甲深度与理论破甲深度对比如表6所示。

表5 编号i后射流均断裂时的总破甲深度

表6 仿真破甲深度与理论破甲深度比较

从表4和表6可以看出：当无干扰射流微元占比大于90%时，采用Pi-1+Ptot/2估算法求得的破甲深度与仿真结果的误差较大；当无干扰射流微元占比为18%～80%时，采用Pi-1+Ptot/2估算法求得的破甲深度与仿真结果误差小于6%，可以用该方法对射流侵彻移动靶的破甲深度进行估算。

2.5 理论与试验对比分析

为了进一步验证理论模型，选用Marmor等[17]的试验数据进行对比分析。Marmor等采用240 mm滑膛迫击炮作为移动靶的发射装置，移动靶结构分别为120 mm×190 mm×300 mm的均质装甲钢(RHA)和1020中碳钢。本文设计一种80 mm聚能装药，成型射流的头部速度为6 900 m/s、尾部速度为2 100 m/s. 共进行3组射流垂直侵彻移动靶板试验。试验相关数据及理论结算结果如表7所示。

表7 试验破甲深度与理论破甲深度比较

Marmor等[17]认为，射流速度和直径从头部至尾部是线性变化的，因此利用本文建立的模型计算时，也按照这个假设进行。本文针对每一种试验工况分别进行了侵彻深度计算。从表7中可以看出，由于试验中靶板的厚度为120 mm，射流刚好穿透了靶板，无法获得最终的侵彻深度，采用本文建立的理论模型计算得到工况1下理论破甲深度为131 mm. 在工况2下，由于炸高为1 600 mm(20Dc)，射流在着靶前已经发生了断裂，侵彻深度也会急剧下降，试验与理论误差为6.9%. 在工况3下，采用的靶板是1020中碳钢，屈服强度约为250 MPa，该类钢的阻抗要明显低于RHA，因此射流对中碳钢的开孔孔径要大于RHA。从理论模型可以看出，孔径是影响射流侵彻深度的关键因素，靶板屈服强度越小，开孔孔径越大，从而会有更多的射流完成有效侵彻，这是射流对中碳钢的侵彻深度明显大于RHA靶板侵彻深度的主要原因。

3 结论

本文通过分析射流微元对高速厚壁靶板的开孔孔径、横向干扰速度来判断不受干扰的射流微元数量，提出了一种用微元法计算射流侵彻高速移动钢靶的侵彻深度方法。基于仿真分析和Marmor等[17]的试验结果，对理论模型进行了验证。得到主要结论如下：

1)采用聚能装药来对付高速移动的厚壁靶板是一种有效的攻击方式，利用微元法计算可以较精确地计算出射流微元的运动状态和受干扰后射流的侵彻能力。

2)靶板运动速度越高，对射流微元的干扰越明显，射流侵彻威力下降越快。主要原因是靶板运动速度决定了不受干扰射流的长度，随着靶板横向运动速度的增加，未受到靶板干扰的射流微元越少，受干扰的射流微元越多，射流受干扰后部分会与孔壁碰撞而无法形成有效侵彻。

3)所建立的理论模型可对反厚壁导弹战斗部设计提供一定指导。在设计破甲战斗部时应尽可能提高射流头部速度和直径，从而增大射流在靶板上的开孔孔径，有利于更多的射流微元完成有效侵彻。