基于数值模拟的上向扇形孔孔底距优选研究

宋 飞，李祥龙，段应明，孙进辉，万再春

（1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2.玉溪矿业有限公司，云南 玉溪 653405；3.云南迪庆矿业开发有限责任公司羊拉铜矿，云南 迪庆 674507）

SONG Fei1,LI Xianglong1,DUAN Yingming2,SUN Jinhui3,WAN Zaichun3(1.Faculty of Land and Resources Engineering,Kunming University of Science and Technology,Kunming 650093,Yunnan,China;2.Yuxi Mining Company Ltd.,Yuxi 653405,Yunnan,China;3.Yunnan Diqing Mining Development Co.Ltd.of Yangla Copper deposit,Diqing 674507,Yunnan,China)

爆破是采矿工艺中的重要环节，爆破质量是个综合指标，大块率、粉矿率、块度均匀程度等都是重要指标。而决定爆破质量的主要因素为爆破参数，爆破参数的不合理会产生爆破效果不佳、爆破生产效率降低以及放出矿石损失贫化率较为严重等问题[1-3]。目前国内外多数矿山都面临着大块率过高和采场生产成本过高等一系列的问题，因此，优化爆破参数的研究迫在眉睫[4]。

随着计算机技术的不断进步，数值模拟在对爆破效果进行预测评价时运用已成为一种主流，且在越来越多的领域获得广泛应用[5-6]。田振农等[7]通过模拟岩土中的爆破问题，得到在爆破应用中数值模拟的准确性与稳定性；刘优平等[8]用ANSYS/LSDYNA软件通过改变装药量和耦合系数，确定了深孔爆破的最佳炮孔装药结构；高辰阳等[9]用ANSYS/LS-DYNA软件构建模型，确定在单自由面下柱状药包的最佳埋深参数。

研究主要以云南某矿爆破漏斗试验为前提，为减少现场的成本和时间，应用ANSYS有限元软件构建模型，在LS-DYNA中观察爆破过程下不同参数同一时间的应力云图变化。进一步研究孔底距应力分布问题，分析在特定单元有效应力对比情况，最终得出最优爆破参数。

1 矿区背景

试验场地为云南德钦县羊拉铜矿，该矿矿体走向长约370 m，工程控制长为250 m，倾向延深约292 m。围岩以花岗闪长岩为主，次为石英岩。矿体厚4.5～50 m，平均为20.54 m，变化系数58.75%，属稳定。金属品位0.3%～6.72%，平均1.16%，变化系数53.49%，属均匀[10]。

具体场地在矿山KT6矿体采场3390水平实施。该矿体走向为北东，倾向北西，倾角一般50°～70°。矿体出露标高3 209～3 460 m。矿体位于F4与F4-1断裂之间，为中厚层大理岩、变质石英砂岩型矿，含矿岩性以夕卡岩为主，属中等稳固。

表1 矿岩物理力学性质Tab.1 Physical and mechanical properties of ore and rock

2 参数筛选

通过在该矿选取与采场岩性相符的巷道中，进行单孔爆破、变孔距爆破和斜面台阶爆破漏斗三组试验。试验结果如下：小型爆破漏斗中以埋深0.68 m，漏斗半径0.58 m，炸药单耗1.78 kg/m3，最小抵抗线0.70 m为最优[11]。通过推算得到深孔爆破参数为最大孔距1.8m，排距1.4m。试验采用药卷直径32mm、长200 mm，重为200 g的球形药包，结合该矿回采落矿时实际选用90机钻凿深孔，装药直径为65 mm，遵循利文斯顿的观点，计算比例得到65 mm直径球形药包长度为406.25 mm，重为1 607.9 g。结合变孔距同段爆破漏斗试验结果，孔间距为最佳爆破漏斗半径1.53 倍，得到如式（1）、式（2）所示[4]。

式中：a为孔底距，m；Q0和Q1为爆破漏斗试验和实际工程的药包质量，kg；r0和r1为爆破漏斗试验和实际工程的漏斗半径，m；W0和W1为斜面台阶爆破和实际工程的最小抵抗线，m。

为了保证爆破参数的准确性和科学性，在保持抵抗线为1.4 m不变的情况下，得出孔底距的参数范围为2.2～2.8 m，后期借助数值模拟的手段进一步将参数确定下来，以减少现场试验的成本和时间。模型方案与前期试验所得数据相结合，试验方案计算模型参数见表2。

表2 计算模型参数 mTab.2 Parameters for calculation model

3 数值计算

3.1 岩体模型

在对岩石材料选用上，选取与应变率相关的材料模型（*MAT_PLASTIC_KINEMATIC）。塑性随动强化模型是建立在Cowper-Symonds关系式基础上的，屈服应力通过应变率相关的参数来表示，如式（3）所示[11]。

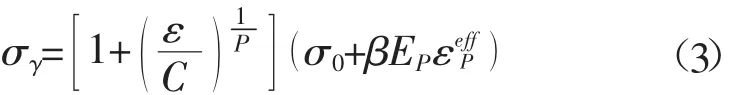
式中：σ0为初始屈服应力，MPa；ε 为应变率为有效塑性应变；EP塑性硬化模量，MPa；C、P为Cowper-Symonds应变率参数。由该式得出式（4）。

式中：E 为弹性模量，MPa；Etan切线模量，MPa；

由于该矿矿场中主要为大理岩、闪岩及变质石英砂岩交混而成，地质条件较为稳定。为了保证数值模拟与现场相吻合，具体的岩体物理力学参数如表3所示。

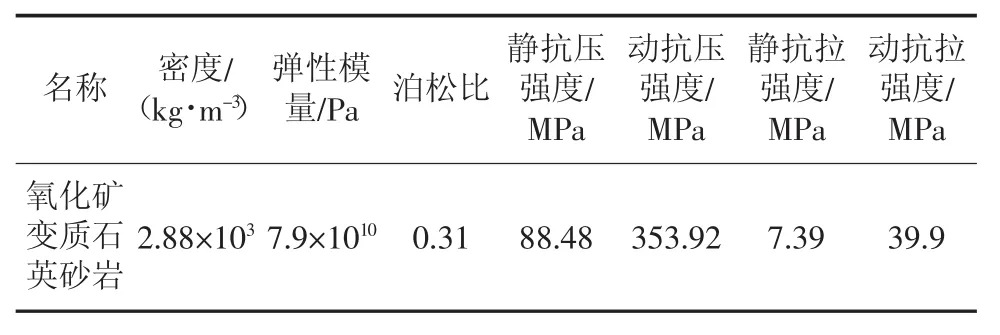
表3 岩体物理力学参数Tab.3 Physical and mechanical parameters of rock mass

3.2 炸药模型

炸药选用2#岩石乳化炸药为爆源，对爆炸过程中压力和比容的关系采用JWL方程描述，采用该状态方程能够较好地描述爆轰产物的膨胀驱动[12]。

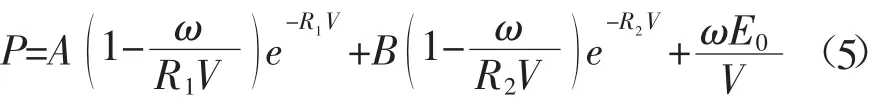
炸药爆炸压力P采用JWL状态方程计算见式（5）所示。式中：P为爆轰气体产物爆炸的压力，Pa；ω为格林艾森参数，即定容条件下压力相对于内能的变化率；A，B 为材料常数，GPa；R1，R2为无量纲常数；V 为爆轰产物的相对体积；E0为初始比内能，GPa。

计算中的2#岩石乳化炸药的JWL状态方程参数见表4。

表4 岩石乳化炸药参数Tab.4 Parameters of rock emulsion explosive

3.3 破坏准则

目前的强度理论主要分为第一类强度理论（以脆性断裂破坏为标志）和第二类强度理论（以塑性屈服破坏为标志）。在工程中比较符合材料介质特性的屈服条件有四种分别为最大剪应力条件（Tresca屈服条件），畸变能条件（Mises屈服条件），摩尔-库伦（Mohr-Coulomb）屈服条件，德鲁克-普拉格（Drucke-Prager）屈服条件。

本文数值模拟处理时所采用的分析标准是Mises屈服准则。Mises屈服条件主要是指在一定的变形条件下，当受力物体内某一单元体的等效应力达到岩石的动态抗拉强度时，认为该单元体处岩石就开始进入塑性状态。

在模拟不同孔网参数的条件下，选定两个炮孔之间的特定单元的应力来判定岩石是否能够发生破坏。由于在炮孔周围由近到远分别为岩石破碎区、裂隙区、震动区。岩石发生破坏的只有压碎区和裂隙区，压碎区距离炮孔较近，岩石肯定破坏。因此只需要判定两个炮孔中间的单元是否处在裂隙区内即可判定岩石是否发生破坏。在裂隙区内岩石受到力的作用主要是受压缩应力，其在径向方向产生压应力，切线方向产生拉应力。一般来说，岩石的抗拉能力都是比较差，故当岩石所受拉伸应力作用超过其动态抗拉强度时，就会在径向方向产生裂隙。

3.4 模型建立

研究计算模型采用3D Solid 164单元类型。在对模型进行简化方面（由于计算模型具有对称性），最终确定的计算模型：长为1 600 mm、宽为140 mm、高为1 800 mm，其中凿岩巷道宽度为420 mm、壁高为240 mm、拱高为287 mm。为简化模型和减小计算量，在模型前、后面施加对称条件，即Z方向的位移约束（将边界的位移及绕边界转动被固定，以使得控制爆破向前、后面发生效果）；在模型左、右及上、下表面处设置无反射边界（为了消除边界效应，以影响模拟效果），创建的模型如图1所示。

图1 计算模型Fig.1 Computational model

4 模型分析

4.1 不同参数下同一时间应力云图分析

为了找到最合适的孔底距参数，确保计算机模拟结构具有科学的理论结果，所以在综合考虑后对不同的孔网参数条件下同一时间内的应力波云图对比分析。根据炸药爆速选取相同孔底距中50ms、60ms、70 ms、80 ms时间下的应力波云图分析研究，应力云图如图2～图5所示。

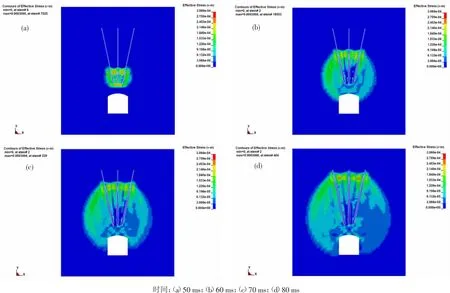
图2 孔底距为2.2 m时应力波云图Fig.2 Stress cloud map（the hole bottom=2.2 m）

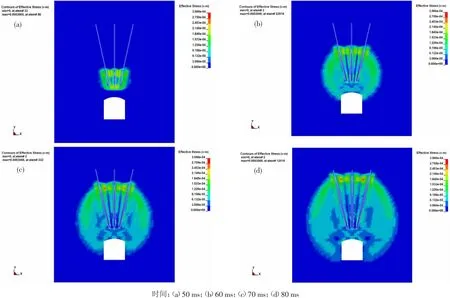
图3 孔底距为2.4 m时应力波云图Fig.3 Stress cloud map（the hole bottom=2.4 m）

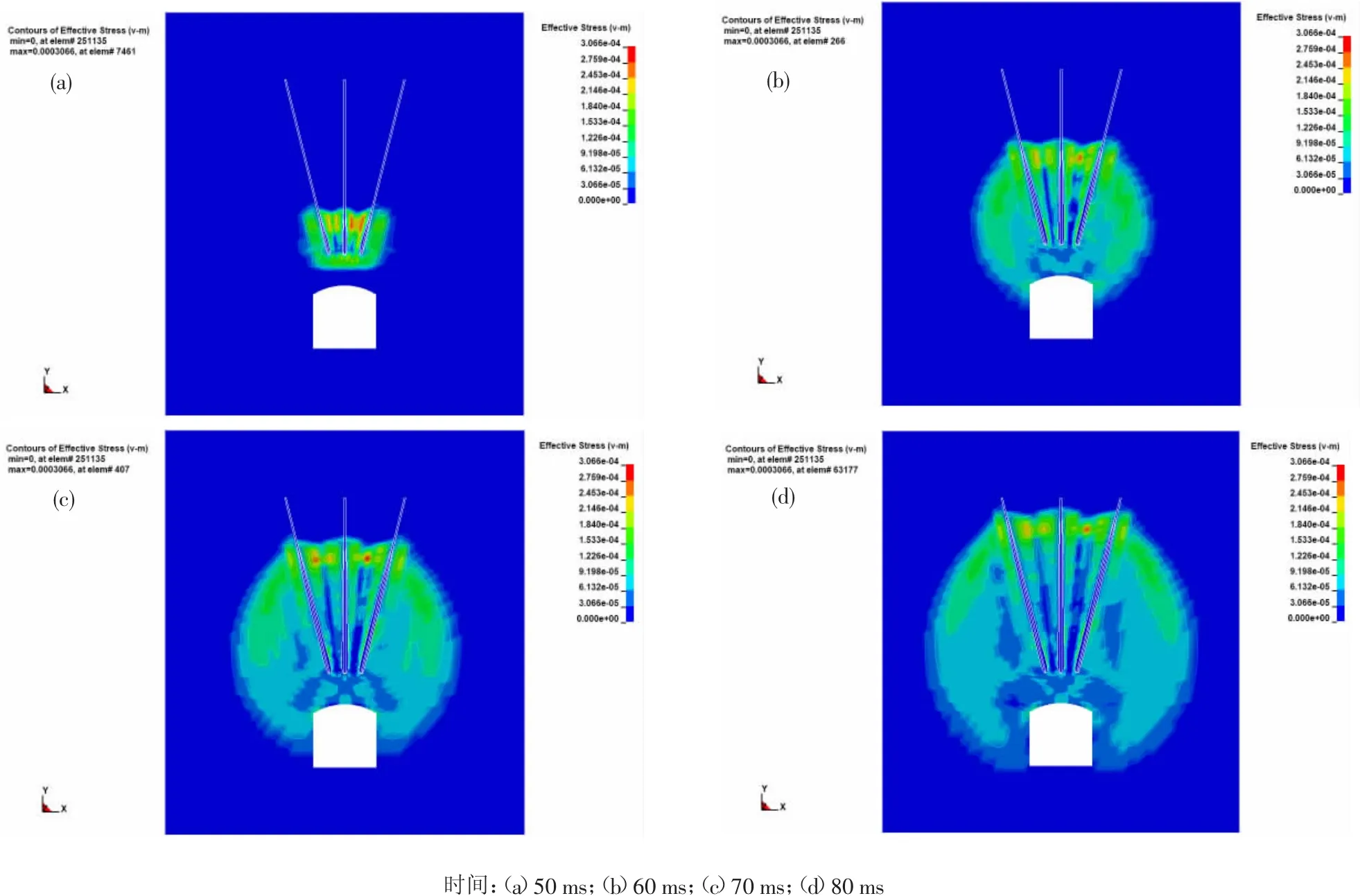
图4 孔底距为2.6 m时应力波云图Fig.4 Stress cloud map（the hole bottom=2.6 m）

在50 ms时的应力云图下，应力波等值线内的应力波颜色深浅基本均匀，这就表明在50 ms时孔距的选取虽然对于应力波的传播有一定的影响，但影响很小，也对爆破效果没有很明显的影响[10]。

在60 ms时的应力云图下，应力波云图的边界所围成的范围发生了大小不一的情况。其中孔底距为2.4 m与孔底距为2.6 m参数下应力波云图所包含的范围大小基本相同，从孔底距为2.2 m与孔底距为2.8 m的范围与孔底距为2.4 m和孔底距为2.6 m的相比较来看，应力波云图所包含的范围明显偏小。这就表明在选取孔底距参数为2.4m和2.6m时，能量分布均匀，说明在此时爆破损伤最大，破岩效果最强。

在70 ms时的应力云图下，孔底距为2.2 m时模型出现了大幅度的能量分布不均匀的情况，而在孔底距为2.4～2.8 m时，能量分布并没有出现像孔底距为2.2 m时的大幅度分布不均的情况。说明在孔底距为2.2 m出现了能量异常的变化。其他三组模型并未出现异样变化，只是随时间的变化能量以正常的方式变化。

在80 ms时的应力波云图下，此刻应力云图已经分布到整个模型，对爆炸能量的利用也都已经达到了最大值。比较应力云图发现在孔底距为2.2 m与孔底距为2.8 m都出现了一部分的淡蓝色区域，这是由于爆破应力过小造成的。而在孔底距为2.4 m与孔底距为2.6 m模型边界与孔底距为2.2 m与孔底距为2.8 m相比较，没有出现如上所示的淡蓝色区域，而且内部为浅绿色，这就表明爆破选取的孔底距参数较为适中，且应力大小较为适中。

4.2 不同参数应力云图完全布满模型时间分析

在对爆破效果进行评价时，在某种程度上应力波传播的速度与出孔网参数对炸药的利用率呈线性正相关，因此对4个模型的应力波传播速度进行分析，即应力波布满模型的时间，如图6所示。

由图6可知，当孔底距为2.2 m等值线应力波布满整个模型时长2 699.3 ms；当孔底距为2.4 m等值线应力波布满整个模型时长2 699.1 ms；当孔底距为2.6 m等值线应力波布满整个模型时长2 599.5 ms；当孔底距为2.8 m等值线应力波布满整个模型时长2 959.2 ms。以布满模型的时间大小为比较，在孔底距为2.2～2.6 m应力波扩散速度最快，说明炸药传播速度最快，利用率高。而孔底距为2.8 m的速度最慢，并且在时间上的差值也较大。

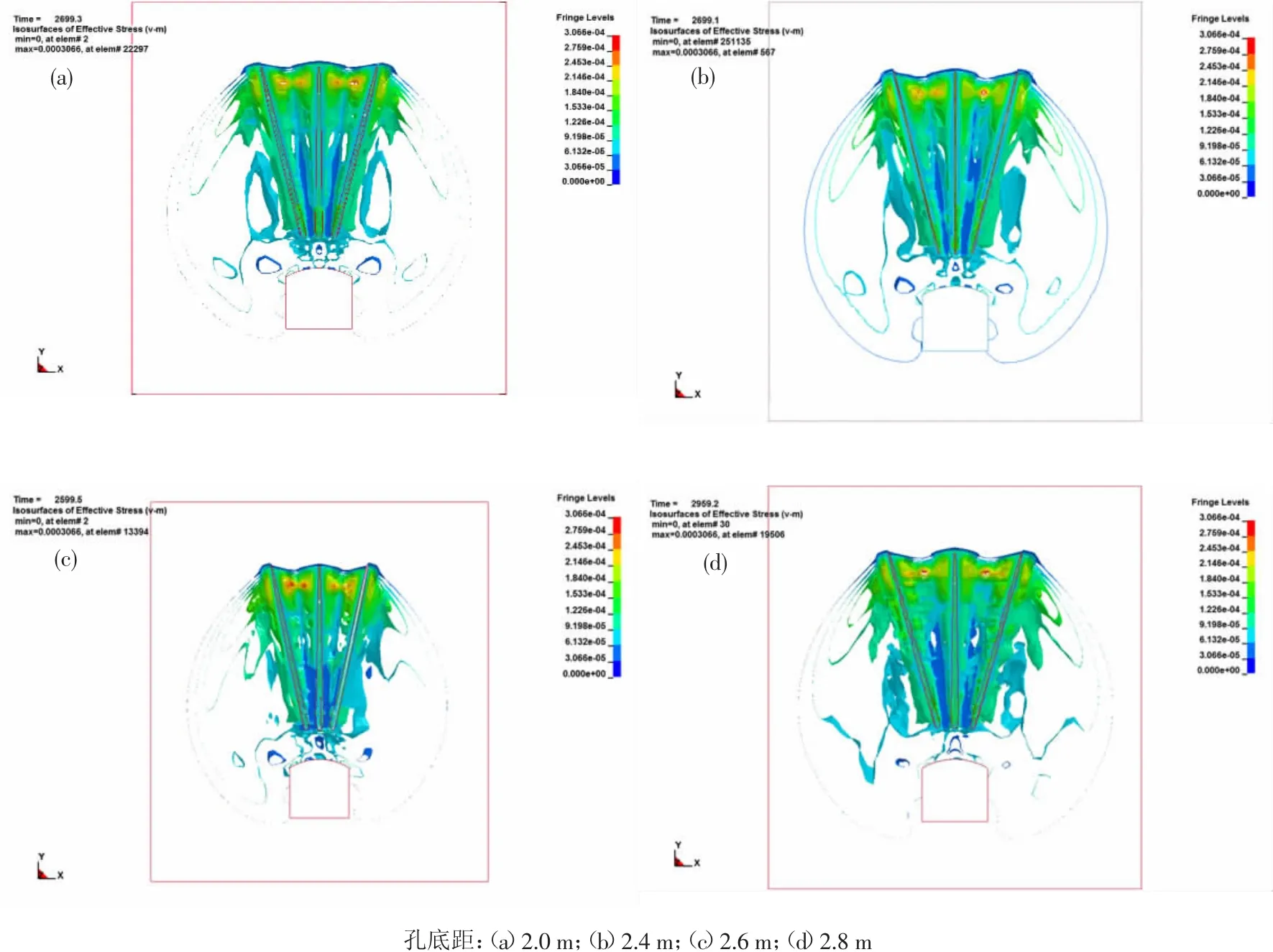
图6 四组模型等值线应力波布满整个模型时的时间Fig.6 Time when four sets of model isoline stress waves fill the entire model

4.3 孔底距特定单元有效应力

为分析不同炮孔间距下的爆破组合作用，对两孔之间矿岩破碎能力的差异进行研究，故采用孔底距为2.2 m的模型。在两个炮孔连线的中心线以及中心线两侧分别取 A、B、C、D、E 五个点，其中 A、B、C、D、E 五个特定单元的单元名分别为 A：H1003、B：H817、C：H673、D：H815、E：H813。为使得选点位置更加清晰将模型颠倒方向观察，分析单元有效应力时程曲线，如图8、图9所示，特定单元位置如图7所示。

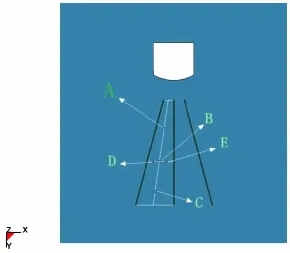
图7 特定单元位置示意图Fig.7 Location diagram for Specific units

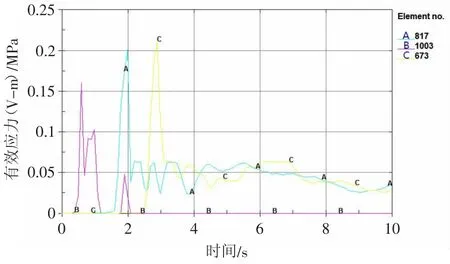
图8 A、B、C纵向特定单元有效应力曲线Fig.8 Effective stress curve of A,B and C longitudinal specific unit

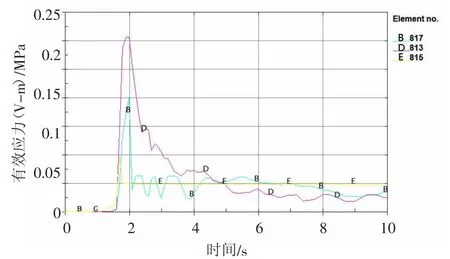
图9 B、D、E横向特定单元有效应力曲线Fig.9 Effective stress curve of B,D and E lateral specific unit

从纵向特定单元有效应力曲线中看出，在前期炮孔底部、炮孔中部及炮孔顶部呈平行增长，且在短时间内应力波的峰值极速增长，但速度上A＞B＞C，与孔底起爆应力波沿扇形孔辐射传播的方式一致。此外，有效应力峰值的大小与A、B、C三点距离孔底的位置成正比，这就表明在爆破作用的有效应力方面，上向扇形孔的孔底处与孔口处相比是偏大的。B、D、E三个特定单元水平分布的应力到达峰值的时间几乎一致，并且有效应力峰值从大到小的排列分别为E点、B点、D点，这就表明在炮孔中心连线的区域，应力波相互叠加导致有效应力加强；而在炮孔中心连线两侧则是一直相反的衰减区域。

4.4 特定单元最大应力值分析

在横向和纵向特定单元应力中，得到孔底处的有效应力大于孔口处。为了更好地将有效应力的大小作为孔网参数优劣的判据，在模型孔底处的同一位置上选取以炮孔对称中心点为特定单元，对这一特定单元的有效应力的最大值进行分析[10]。节点的选择如图10所示，分别记为A和A'。各组有效应力曲线如图11所示，通过对图11中曲线图分析，得出各孔底距特定单元最大有效应力汇总表，如表5所示。

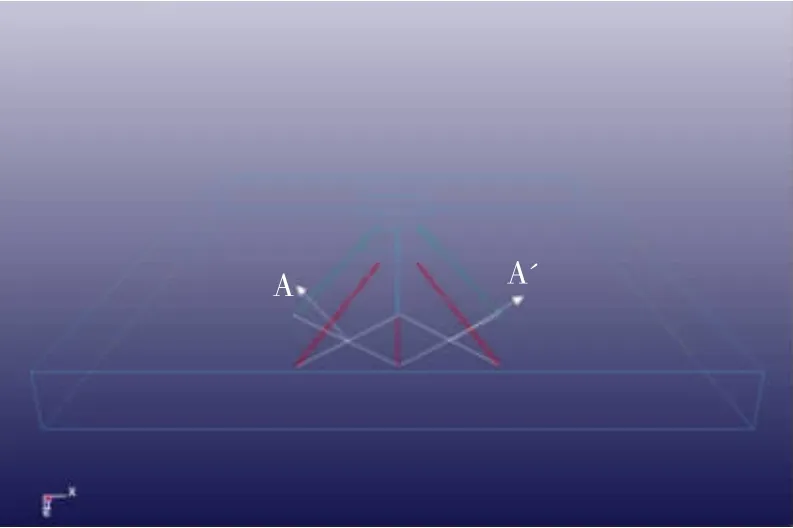
图10 孔底特定单元的选取Fig.10 Selection of specific unit of hole bottom

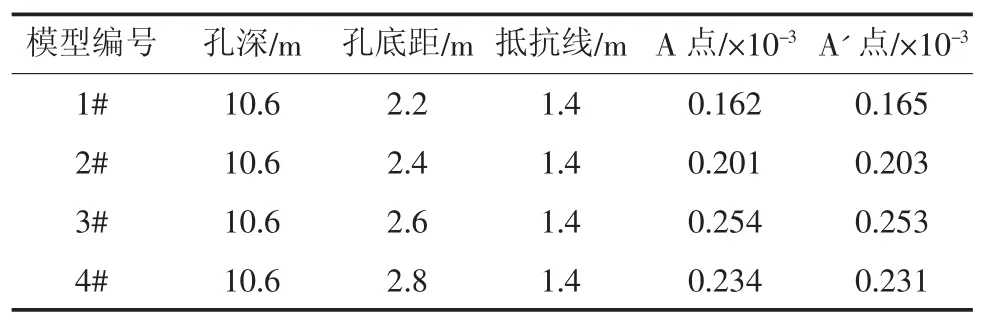
表5 各方案特定单元最大有效应力汇总Tab.5 The maximum effective stress remittance table for each program specific unit

通过对爆炸产生有效应力大小的判断进而分析爆破过程的优劣。由表5所示，最大应力大于矿体抗压强度，故已完全破坏。表明当选择孔底距为2.2 m的孔网参数时爆破产生的有效应力值最低，伴随着孔底距参数的不断增大（2.4 m，2.6 m，2.8 m），有效应力值也不断增大，其峰值出现在孔底距为2.6 m的时候，随后孔底距为2.8 m有效应力值明显降低。

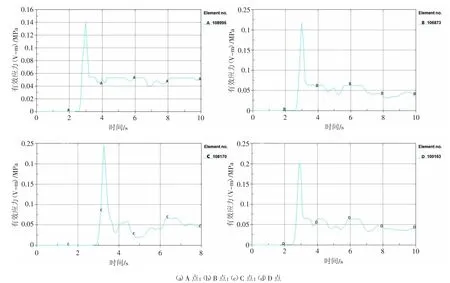
图11 各组有效应力曲线图Fig.11 Effective stress curve

综上所述，通过对设计方案的数值模拟可知，从不同孔底距在不同条件下的应力云图看出，孔底距控制在2.4～2.6 m之间时，炸药产生较好的爆破效果。为了使得孔底距参数更为准确，取模型中的特定单元对有效应力进行分析，最终确定孔底距为2.6m是最优孔底距参数。

5 现场试验

现场采用所选孔网参数进行爆破的范围为一单元矿房，具体位置为3395水平1#凿岩巷、2#凿岩巷、3#凿岩巷、4#凿岩巷、5#凿岩巷、6#凿岩巷。具体装药情况如表6所示。

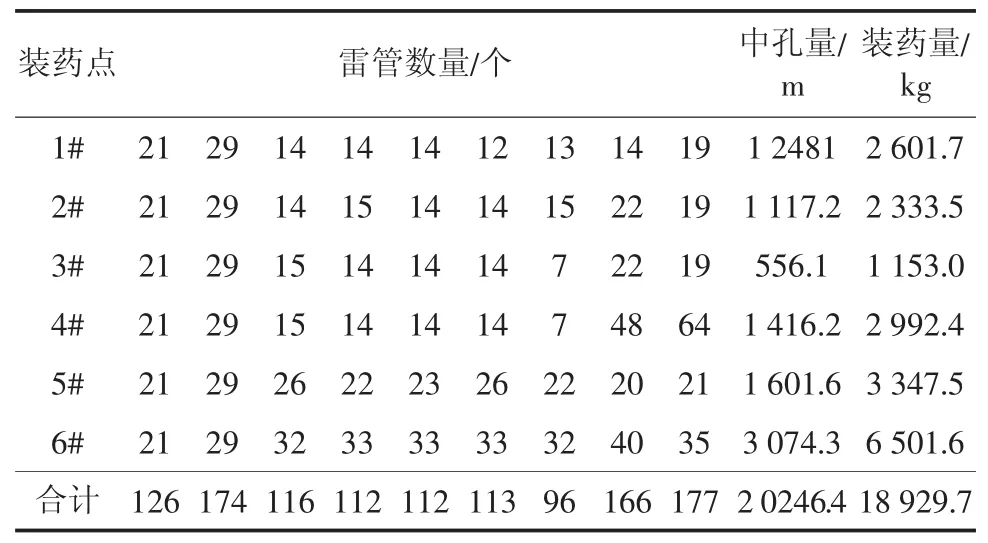
表6 具体装药情况分布Tab.6 The charge points,and segments of detonators hole charge distribution table

爆破后开挖效果统计分析得知：3390水平1#凿岩1～12排巷基本无根底，有少量超挖现象。2#凿岩巷无超挖现象，无根底，采场底板顶板均较为平整。3#凿岩巷有部分超挖现象，无根底，采场顶板有大块掉落。4#凿岩巷1～10排有垮塌现象，部分巷道堵塞，11～13排爆破无垮塌现象，有超挖。5#凿岩巷与6#凿岩巷开挖效果较为理想，无垮塌现象，巷道底板顶板壁帮均保持完整。综上说明，爆破开挖效果较为理想，说明爆破孔网参数选择较为合理。

试验中爆破共崩矿60446T，共使用炸药23670t，炸药平均单耗0.32 kg/t，参考一单元切割槽爆破以及KT5矿体部分盘区爆破单耗0.38～0.42 kg/t。说明爆破效果显著，所选孔网参数为矿山的实际生产节约了成本，提高了效益，对矿山的生产实际具有积极的指导作用。

6 结论

（1）结合试验得出的爆破参数，通过理论及数值模拟综合考虑给出四种不同孔底距参数。

（2）通过有限元软件对孔底距方案进行数值模拟，以分析应力云图来显示爆炸效果，初步得到了孔底距为2.4 m与2.6 m为较优；在结合分析特定单元应力大小显示爆破程度，得出在孔底距为2.6 m的最大应力为0.254；最终确定孔底距为2.6 m是最优孔底距参数。

（3）数值模拟是以有效的模拟爆破过程，针对不同的爆破参数进行合理比较。但由于数值模拟以简化现场为前提，摒弃了井下的复杂条件，无法准确推断参数是否完全符合矿山要求。因此现场验证变得十分关键，需及时得到爆破反馈，调整爆破参数，以便更好地获得适合矿山合理的爆破参数。