扇形孔爆破裂隙的数值模拟
李 斌,许梦国,王文杰
(1.武汉科技大学,湖北 武汉 430081;2.冶金矿产资源高效利用与造块湖北省重点实验室,湖北 武汉 430081)
无底柱分段崩落法是20世纪50年代以来随着新的采矿工艺和设备的出现而逐步发展起来的的一种采矿方法,由于其高效率、高度机械化、工艺简单、生产安全和成本低廉的特点,无底柱分段崩落法在金属矿山得到迅速推广,特别是铁矿山更为广泛。无底柱分段崩落法的采矿机理主要是矿石和围岩的爆破崩落[1]。然而,无底柱分段崩落法在实际爆破落矿过程中会产生较多的大块,不仅增加了成本、降低了采矿效率,还影响了采矿的安全生产。
爆破产生不同块度的岩块可以认为是爆破产生各种裂隙的结果,研究爆破裂隙的产生和传播规律可以帮助更好的了解大块的产生机理。爆破的化学反应过程是炸药从具有高能量的密致物质转化为高压、高温的气体产物[2-3]。近年来通过对岩石爆破的不断研究,国内外专家学者一致认为在岩石爆破过程中,有两类荷载作用在岩石上:爆炸应力波作用和爆生气体膨胀作用[4]。然而,很缺乏对爆破过程中岩石裂隙产生和发展规律的认识,主要原因是爆破过程非常迅速,一般在几个毫秒就结束了,很难对爆破过程进行深入的了解。
为了对无底柱分段崩落法爆破过程进行比较深入的研究,采用非线性显示动力学软件AUTODYN进行爆破模拟,来分析无底柱分段崩落法爆破落矿过程中爆破裂隙的产生和传播规律。
1 数值模拟计算模型
在本文中,采用AUTODYN 2D平面对称建立计算模型,假定岩体是连续、各向同性的。本次模拟的中深孔布置及参数如图1所示,炮孔孔径φ为80mm。
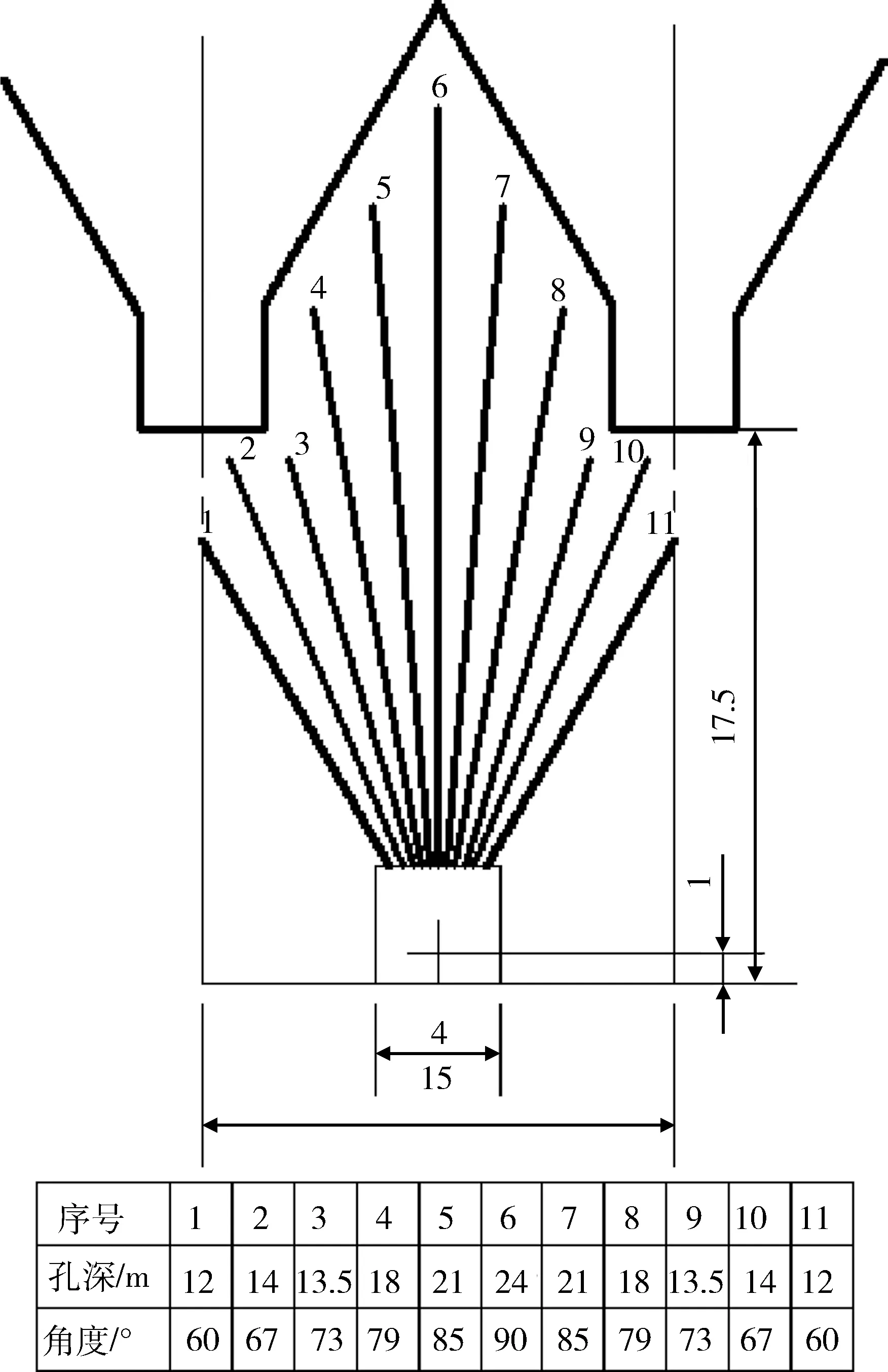
图1 中深孔布置
1.1 材料模型
在本文模拟中用到的材料有两种:岩石(铁矿石)和炸药(ANFO)。
1.1.1 岩石动力学模型
本次模拟某铁矿无底柱分段崩落法中深孔爆破落矿,铁矿石可以认为是脆性岩石,这类脆性材料具有高抗压强度和低抗拉强度的性质,当受到荷载作用时因为微裂隙的扩展而表现出渐进式破坏。针对这种连续介质破坏模型,Johnson和Holmquist[5-7]提出了一种适用于脆性材料的本构模型(J-H模型)。J-H模型可以用来研究脆性材料(如岩石、混凝土和陶瓷等)冲击和爆炸问题。J-H本构模型包括有强度模型和失效模型,在使用J-H本构模型时,必须同时使用其强度模型和失效模型[8]。
具体而言,J-H模型有两种形式:JH-1[9]模型和JH-2[7]模型。JH-1模型主要是用来计算大变形而并没有考虑由于不断增加的变形导致的渐进式破坏。JH-2模型通过添加多节段应力-应变曲线来弥补JH-1模型的不足。
1.1.1.1 多项式状态方程
本文采用多项式状态方程来描述岩石,通常情况下多项式状态方程是和J-H模型一起使用的[10]。岩石在失效前,多项式状态方程可以表示为式(1)。
P=K1μ+K2μ2+K3μ3+ΔP
(1)
式中:P为压力;μ为压缩量,μ=V0/V-1=ρ/ρ0-1,V和ρ代表岩石当前的体积和密度,V0和ρ0代表岩石初始的体积和密度;K1,K2,K3为常数(K1通常是体积模量)。
图2所示为压力P和压缩量μ的关系图,式(1)中的ΔP就是图中的压力增量,ΔP取决于材料的破坏程度,它的值变化范围由D=0时的ΔP=0到D=1时的ΔPmax。D是破坏程度,取值范围为0~1。而对于拉伸应力(μ<0),多项式状态方程表示为式(2)。
P=K1μ
(2)
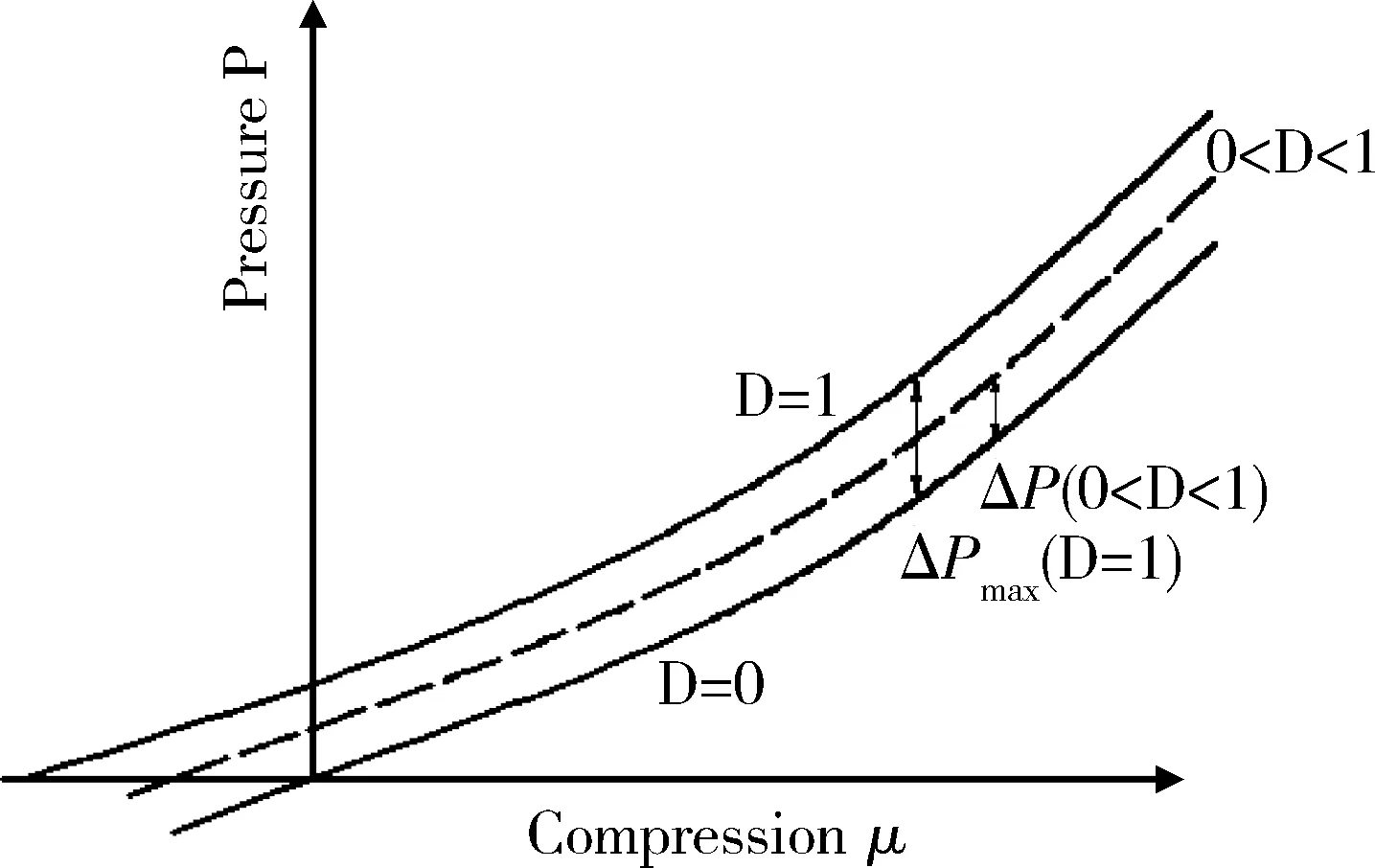
图2 压力P和压缩量μ关系
1.1.1.2 JH-2本构模型
JH-2模型假定材料最初是弹性和各向同性的,满足式(3)。
σij=-p(εkk)δij+2Gξij
(3)
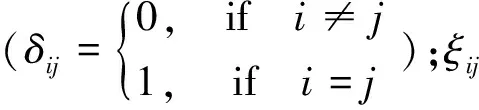
Hugoniot弹性极限时的应力可以有如式(2)所示的关系式。
(4)
式中:pHEL为Hugoniot弹性极限的压力;σHEL为Hugoniot弹性极限的应力。
JH-2模型的强度是服从塑性力学中的米塞斯条件的[10]。即
(5)
式中σ1,σ2,σ3为主应力。
有效应力通常可以用来作为描述弹性极限破坏的标准。对于服从米塞斯条件的模型,有效应力可以表示为式(6)。
(6)
完整材料的破坏强度表达式为式(7)。
(7)
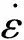
(8)

材料完全破坏时的强度表达式为式(9)。
(9)
式中B,C,M为材料常数。
材料在破坏过程中的强度表达式为式(10)。
(10)
式中D为当前的破坏程度。
破环程度随时间变化的关系式为式(11)。
(11)
式中等效塑性应变εf的表达式为式(12)。
εf=D1(p*+T*)D2
(12)
式中D1和D2为材料的破坏常数。
1.1.2 确定JH-2模型材料参数
岩石材料的强度一般是应用Koek-Brown失效标准来评估,尤其是像铁矿石这类坚硬岩石[11]。作为一个经验公式,Koek-Brown失效标准的表达式[12]为式(13)。
(13)
式中:σ1和σ3为三轴试验中的轴向应力和侧向应力;σc为单轴抗压强度;m和s为与材料有关的常数,本文模拟的是完整岩石材料,s取1.0,根据文献[12],m取32。
在研究动力学问题时通常需要采用动态强度,动态强度可以超过相对应静态强度一个甚至数个数量级[13-14],在本次模拟中选取动态强度是静态强度的10倍。可以得到岩石的基本参数如表1所示。

表1 岩石的基本参数
岩石材料常数A和N根据文献[11]按照式(7)进行曲线拟合,得到的数据分别为0.86和0.63。考虑到难测取岩石完全破坏时的数据,这里假定残余强度为完整岩石强度的30%[15],得到B和M的值分别为0.29和0.63。参照其他脆性材料的破坏参数,D1和D2选取为0.006和0.8。应变率常数C是随研究材料而变化的,Johnson GR研究的玻璃的C值为0.003[16],Holmquist TJ研究的碳化硅的C值为0.009[17],由于缺乏铁矿石这方面的研究数据,参照以上数据将本次研究的C值选取为0.006。
1.1.3 炸药模型
本次模拟采用的炸药为ANFO。描述爆炸产物的状态方程很多,然而应用最普遍的是JWL(Jones-Wilkins-Lee) EOS[18],JWL EOS是描述高能炸药爆轰产物压力-体积关系的状态方程,JWL状态方程的P-V关系如式(14)所示。
(14)
式中:P为压力;A、B、R1、R2、ω为炸药常数;V是爆炸产物的相对体积;E0为初始内能密度。
本次研究采用的ANFO炸药各参数如表2所示。

表2 ANFO炸药参数
1.2 计算模型
ANSYS AUTODYN在研究岩石破坏方面有了成功的应用案例[19-20]。在本次研究中,建立的计算模型如图3所示。
图3中绿色区域代表岩石,蓝色条状代表ANFO炸药,红色标记点为炸药起爆点(孔底起爆),11个炮孔同时起爆,数字标记点为高斯点,边界条件为无反射边界,边界材料为岩石。模型尺寸为24000mm×42000mm,考虑到炮孔直径为80mm,以及计算机性能,按40mm×40mm划分网格,总共有630000个单元。由于模型是关于炮孔6对称的,故只在炮孔6~11之间布置高斯点,这些高斯点设置在孔底、孔口和中间位置,分别用来研究孔底、孔口和中间部位的爆破过程。为便于后面的数据记录和分析,每个部位的高斯点纵坐标一样,为尽量获取较多的数据,横坐标间距40mm。
2 模拟结果
基于以上计算模型、状态方程、JH-2本构模型和相关参数,在AUTODYN中进行计算,计算到3475次时爆破已到孔口位置,可以认为爆破过程基本完成了,得到的材料状态如图4所示。
从图4中可以明显观察到:孔口位置产生非常密集的爆破裂隙,中间位置爆破裂隙也比较密集,而在靠近孔底位置爆破裂隙显得很稀疏,特别是中间5个炮孔之间。可以认为岩石在孔口位置破坏程度比较大,而在孔底位置破坏程度较小。
在应力波作用下岩石的破碎过程主要由两方面决定:①应力波产生的最大应力;②应力波的比冲能和比能[21]。这里主要从最大爆破应力来分析研究扇形中深孔的爆破过程。
从图3可以看出,炮孔布置是以炮孔6对称的,考虑到炮孔6、7、炮孔7、8、炮孔8、9和炮孔10、11相邻孔布置形式一样,就选取炮孔7、8之间的岩石作为研究对象,以及布孔形式有差异的炮孔9、10。
2.1 孔底爆破过程分析
统计孔底位置高斯点的最大爆破应力,如图5所示。
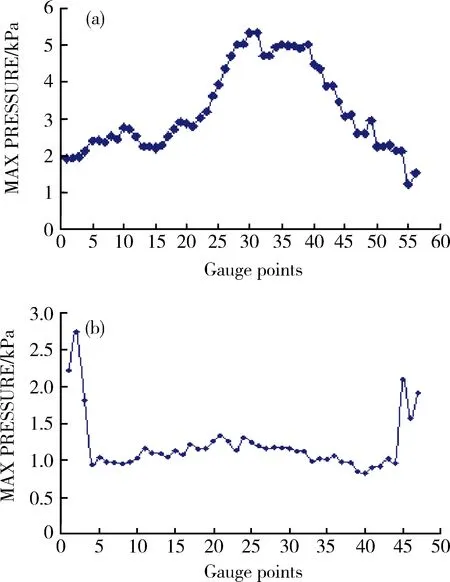
图5 孔底最大爆破应力统计
图5中(a)、(b)分别是炮孔7和炮孔8之间孔底,炮孔9和炮孔10之间孔底最大爆破力统计图。图5中可以观察到,(a)曲线呈现两边低中间高的现象,平均最大爆破应力值为:3.2385GPa,而(b)曲线却不同,呈现两边高中间低的现象,平均最大爆破应力为1.2062GPa。
炮孔8孔底到炮孔7的水平距离为2200mm,布置高斯点57个。图6中3号高斯点靠近炮孔7,56号高斯点靠近炮孔8,28号高斯点位于这段研究距离的中间位置。从56号高斯点应力曲线图可以看出炮孔8在0ms时爆破到这个位置,爆破应力急剧上升并达到最大值;从3号高斯点应力曲线图炮孔7在0.5ms时爆破到这个位置,爆破应力急剧上升并达到最大值;从28号高斯点应力曲线可以看出在最大应力出现前有一段平稳应力值较小的曲线,这是炮孔8爆破应力波到达这个位置造成的,随后炮孔7爆破应力波达到,而后应力急剧上升并到达最大值,该值将近是3号和56号高斯点最大爆破应力的3倍。从而出现了炮孔中间位置的最大爆破应力比靠近炮孔位置高的现象。
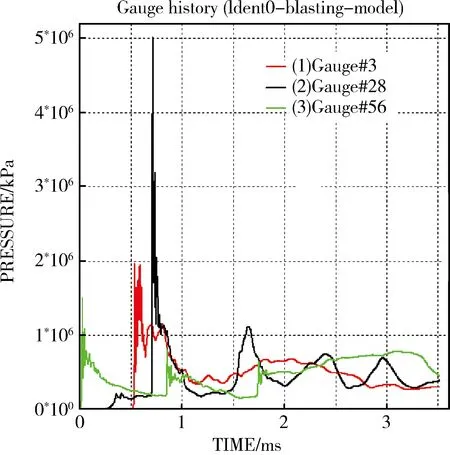
图6 爆破应力曲线(3、28和56号高斯点)
炮孔10孔底到炮孔9的水平距离为1860mm,布置高斯点48个。图7中2号高斯点靠近炮孔9,47号高斯点靠近炮孔10,24号高斯点位于这段研究距离的中间位置。炮孔9和炮孔10都在0ms时爆破到这个位置,2号、47号高斯点爆破应力急剧上升并达到最大值;24号高斯点处炮孔9和爆破产生的应力波几乎同时到达,产生一系列的波峰和波谷,但是叠加后的爆破应力却不到2号和47号高斯点最大爆破应力的一半。从而出现了中间曲线值较小的现象。
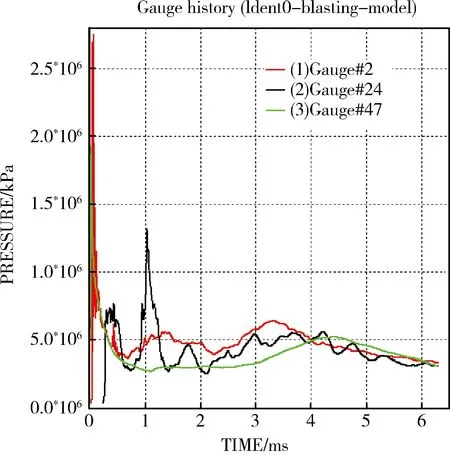
图7 爆破应力曲线(2、24和47号高斯点)
通常情况下,孔间距越小爆破效果越好,而这里模拟的结果发现2200mm孔间距的平均最大爆破应力达到1860mm孔间距的2.5倍,造成这种情况的原因就是起爆时间的间隔。炮孔9和炮孔10几乎同时起爆,其孔底位置有很好的应力波叠加或碰撞,然而最大应力却偏小;炮孔8提前炮孔7约0.5ms爆破,炮孔8爆破应力波优先在孔底位置传播,其作用降低了这部分岩石的强度和完整性,当随后炮孔7爆破产生的应力波到达时,岩石得到很大程度的破坏。Liqing Liu和P.D.Katsabanis的研究[22]提出:相邻炮孔同时起爆时应力波的叠加和碰撞会加强对岩石的破坏能力,当起爆间隔超过50μs时,最大爆破应力相比降低了46%。本文的研究结果却截然相反,在这里对后者提出质疑。
2.2 中间位置爆破过程分析
统计炮孔中间位置高斯点的最大爆破应力,如图8所示。
图8中(a)、(b)分别是炮孔7和炮孔8之间中间位置、炮孔9和炮孔10之间中间位置最大爆破力统计图。可以观察到,图8中(a)曲线与图5中(b)曲线非常相似,但是中间曲线更平稳,平均最大爆破应力值为2.5700GPa;而图8中(b)曲线呈现两边向中间递减的现象,平均最大爆破应力为2.8741GPa。
炮孔7和炮孔8中间某部位的水平距离为1440mm,共计37个高斯点。图9中58号高斯点靠近炮孔7,91号高斯点靠近排孔8,75号高斯点位于这段研究距离的中间位置。炮孔8提前炮孔7约0.4ms起爆,从91号高斯点应力曲线可以观察到,随着炮孔8的爆破,靠近炮孔8的地方爆破应力急剧上升并达到最大值;从58号高斯点曲线可以看出,当炮孔8爆破应力波达到后炮孔7才开始爆破,然后应力急剧上升达到最大值;从75号高斯点曲线可以看出,在0.8ms左右炮孔8产生的应力波到达这位置,应力峰值达到1.8GPa,在1.1ms左右炮孔7产生的应力波到达,达到最大应力2.2GPa,增加量很小。对比图6可以发现,随着炮孔间距的减小,最大爆破应力却呈现降低的现象,这是因为炮孔间距的降低,当炮孔8产生的爆破应力波作用岩石时,产生较大的应力使岩石产生一定程度的破坏(包括爆破裂隙和自由面),从而降低了炮孔7应力波的作用。

图8 孔底最大爆破应力统计

图9 爆破应力曲线(58、75和91号高斯点)
炮孔9和炮孔10中间某部位的水平距离为1270mm,共计33个高斯点。图10中80号高斯点靠近炮孔9,78号高斯点靠近炮孔10,64号高斯点位于这段研究距离的中间位置。由于炮孔倾斜角度的影响在这个水平产生了大约0.1ms的爆破间隔,可以发现图10 与图9中的曲线非常相似,主要不同是图10中64号高斯点的最大爆破应力(2.3068GPa)出现在第一个波峰,接着第二个应力波到达造成第二个波峰(爆破应力约为1.9GPa)。
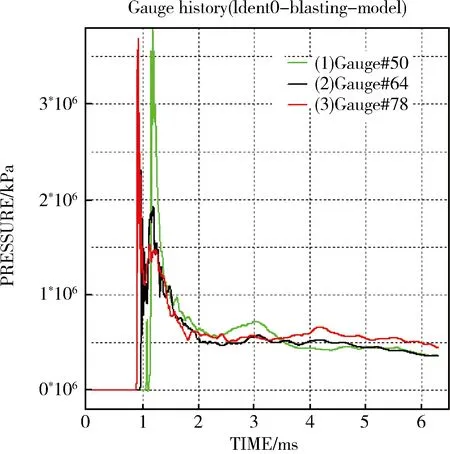
图10 爆破应力曲线(50、64和78号高斯点)
通过以上分析可以得出:当相邻炮孔的间距减小到某一程度时,由于起爆之间的间隔,第一个应力波在岩石中传播时就会对岩石产生一定程度的破坏,降低了第二个应力波对岩石的作用,并且随着距离的减小,第一个应力波产生的爆破应力越大,第二个应力波产生的应力波就越小。
2.3 孔口爆破过程分析
统计炮孔孔口位置高斯点的最大爆破应力,如图11所示。
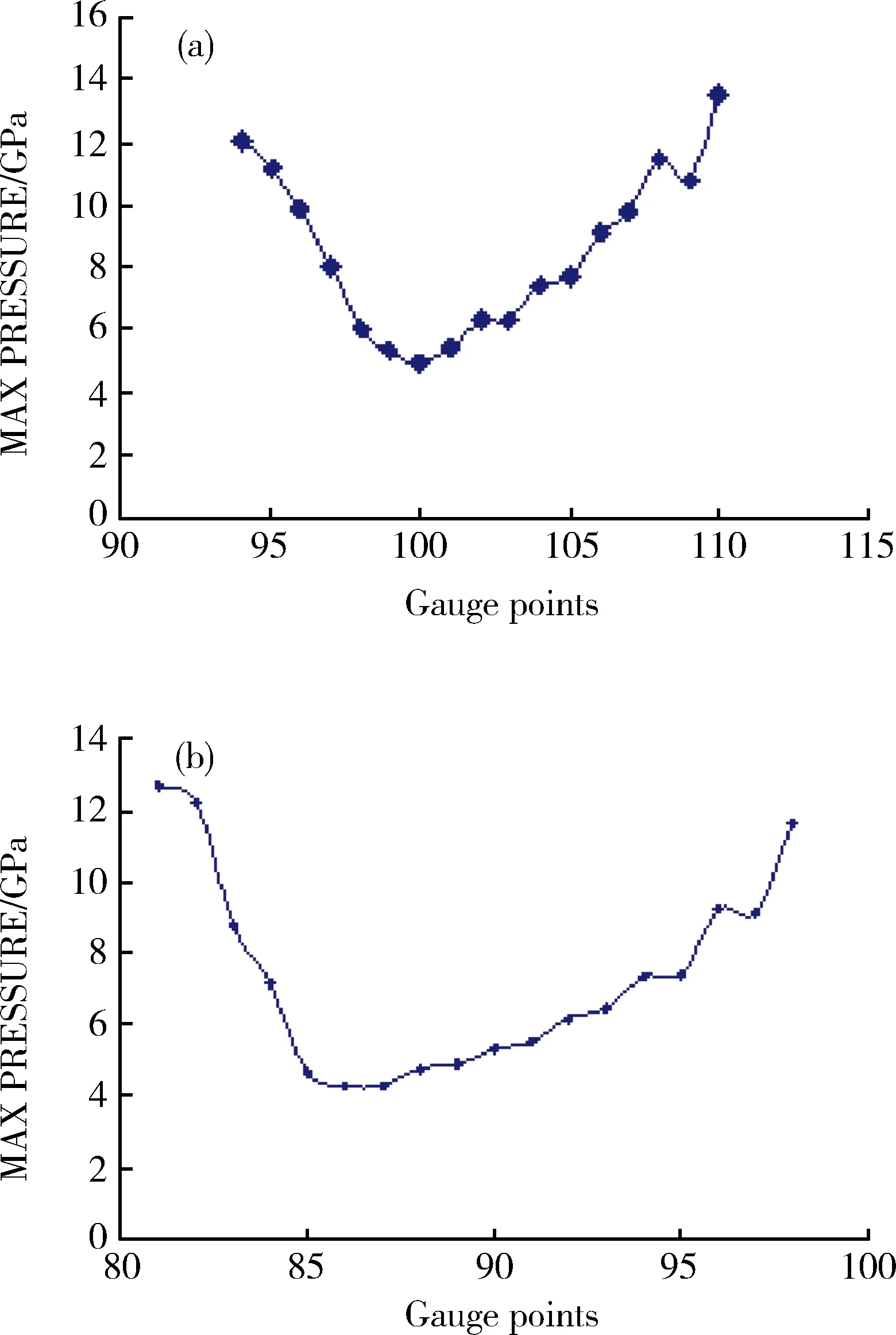
图11 孔口最大爆破应力统计图
图11中(a)、(b)分别是炮孔7和炮孔8之间孔口、炮孔9和炮孔10之间孔口最大爆破力统计图,平均最大应力分别为8.5367GPa和7.3526GPa,两条曲线非常相似,呈现U形。
炮孔8孔口到炮孔7的水平距离为660mm,共计17个高斯点。图12中95、97号高斯点靠近炮孔7,107、109号高斯点靠近炮孔8,从图12中可以看出,107、109号高斯点的最大爆破应力是由炮孔8爆破应力波造成的,95、97号高斯点的最大爆破应力是由炮孔7爆破应力波造成的,并且里炮孔越近最大爆破应力越大,从而出现了图11中的U形曲线。炮孔9和炮孔10之间的孔口位置情况与此类似,这里就不再赘述。

图12 爆破应力曲线(95、97、107和109号高斯点)
3 讨论
在孔底位置,由于炮孔间距比较大,单个应力波作用岩石产生的最大爆破应力较小,若相邻炮孔同时起爆,两个应力波叠加和碰撞作用可以使中间部分岩石的最大爆破应力达到靠近炮孔岩石最大爆破应力的一半左右;而当相邻炮孔间隔起爆时,由于前一个炮孔爆破应力波(小于岩石的静态单轴抗压强度)作用,降低了中间岩石的强度及完整性,当第二个应力波达到时,岩石受到的爆破应力大幅度上升并到达最大值,其值可以达到靠近炮孔岩石最大爆破应力的3倍。在前期的现场分析中[23],同条进路相邻5排炮孔,相同的爆破工艺,前3排岩石的完整性比较好,爆破产生较多的大块,而后2排岩石受到前排爆破的影响,完整性较差、顶板比较破碎,爆破效果很好,基本上没有大块的出现。这说明完整性很好的岩石受到爆破应力波作用降低强度后,当再次有爆破应力波作用时可以很好的破碎岩石。在文献[24]中,大块主要出现在孔底位置,可见改善相邻炮孔孔底之间的最大爆破应力非常重要。
当相邻炮孔间距减小时,第一个应力波作用岩石的应力较大(超过岩石的静态抗压强度)时,岩石会产生一定程度的破坏,降低了第二个应力波的作用,并且当第一个应力波产生的应力越大时,第二个应力波的作用越小。
在孔口位置,由于相邻炮孔间距很小,岩石的最大爆破应力主要是由距离近的炮孔爆破应力波作用造成,距离炮孔越近,最大爆破应力越大。
4 结论与展望
本文应用AUTODYN进行扇形孔爆破模拟,主要通过分析炮孔之间的最大爆破应力产生机理来解释岩石爆破裂隙的分布状态,主要有以下结论。
1) 炮孔越是密集的位置,爆破应力越大,爆破裂隙也越多,从图4中可以清晰看到这一点,这就意味着孔底位置可能有大块的出现。
2) 相邻炮孔间距较大时,尤其是孔底位置,应避免同时(或间隔时间很短)起爆,而应该确定合理的间隔时间,进行间隔起爆。
3) 相邻炮孔间距较小时,间隔起爆的作用就不明显了,岩石受到的最大爆破应力主要受距离近的炮孔爆破应力波的影响。
为改善扇形孔的爆破质量,下一步的工作就是确定合理的炮孔间距范围,以及对应不同孔间距的起爆时间间隔。
[1] D.Brunton,S.J.Fraser.Parameters influencing full scale sublevel caving material recovery at the Ridgeway gold mine[J].International Journal of Rock and Mining Sciences,Volume 47,Issue 4,June 2010:647-656.
[2] Bhandari S.Engineering rock blasting operations[M].Brookfield;A.A.Balkema,1997.
[3] Fourney WL.Mechanisms of rock fragmentation by blasting.Comprehensive rock engineering[M].Vol.4,ed J.A.Hudson,(Pergamon),1993:39-69.
[4] H.K.Kutter,C.Fairhurst.On the fracture process in blasting[J].International Journal of Rock Mechanics and Mining Science,Volume 8,Issue 3,May 1971:181-188.
[5] Holmquist TJ,Templeton DW,Bishnoi KD.Constitutive modeling of aluminum nitride for large strain,high-strain rate,and high-pressure applications[J].Int J Impact Eng,2001,25:211-231.
[6] Johnson GR,Holmquist TJ,Beissel SR.Response of aluminum nitride(including a phase change) to large strains,high strain rates,and high pressures[J].J Appl Phys,2003,94(3):1639-1646.
[7] Johnson GR,Holmquist TJ.An improved computational constitutive model for brittle materials.In:Schmidt SC,Shaner JW,Samara GA,Ross M,editors.High pressure science and technology-1993[M].Woodbury,NY:AIP Press;1994.p.981-4.
[8] Century Dynamics Inc.AUTODYN Theory Manual,Revision 4.3[M].Concord,California,2005.
[9] Johnson GR,Holmquist TJ.A computational constitutive model for brittle materials subjected to large strains,shock-wave and high strain-rate phenomena in materials.Ed.M.A.Meyers,L.E.Murr and K.P.Staudhammer,Marcel Dekker lnc[M].New York,1992,PP.1075-1081.
[10] M.M.Dehghan Banadaki,B.Mohanty.Numerical simulation of stress wave induced fractures in rock[J].International Journal of Impact Engineering,40-41(2012):16-25.
[11] Hoek E,Brown ET.Practical estimates of rock mass strength[J].International Journal of Rock Mechanics and Mining Sciences,1997;34(8):1165-1186.
[12] Hoek E,Brown ET.Underground excavations in rock[M].London:Institute of Mining and Metallurgy,1980.
[13] Rinehart JS.Dynamic fracture strength of rocks.Proceedings of the seventhsymposium on rock mechanics[M].Pennsylvania State University,1965.
[14] Prasad U,Mohanty B,Nemes J.Dynamics strength and fragmentation in selected rocks under impact loading.In:Girard J,et al.,editors.Proceedings of the fourth North American rock mechanics symposium—NARMS 2000[M].Rotterdam:Balkema;2000.p.577-582.
[15] G.W.Ma,X.M.An.Numerical simulation of blasting-induced rock fractures[J].International Journal of Rock Mechanics and Mining Sciences,2008(45):966-975.
[16] Johnson GR,Holmquist TJ.Response of boron carbide subjected to large strains,high strain rates,and high pressures[J].J Appl Phys,1999(85):8060-8063.
[17] Holmquist TJ,Johnson GR.Characterization and evaluation of silicon carbide for high-velocity impact[J].J Appl Phys,2005;97:93502-1—93502-12.
[18] Lee EL,Hornig HC,Kury JW.Adiabatic expansion of high explosive detonation products.Report NO.UCRL50422.California Univ[M].United States:Lawrence Radiation Lab;1968.
[19] Zheming Zhu,Bibhu Mohanty,Heping Xie.Numerical investigation of blasting-induced crack initiation and propagation in rocks[J].International Journal of Rock Mechanics and Mining Sciences,2007(44):412-424.
[20] Chen SG,Zhao J.A study of UDEC modeling for blasting wave propagation in joint rock mass[J].International Journal of Rock Mechanics and Mining Sciences,(35)1998:93-99.
[21] 钮强.岩石爆破机理[M].沈阳:东北工学院出版社,1990.
[22] Liu Liqing,P.D.Katsabanis.A numerical study of the effects of accurate timing on rock fragmentation[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(5):817-835.
[23] 李斌,许梦国.无底柱分段崩落法大块产生机理与解决措施[A].王运敏.中国采选技术十年回顾与展望[C].北京:冶金工业出版社,2012.

