基于越野工况预测的混合动力履带车辆能量管理策略

许绍航， 席军强， 陈慧岩

(北京理工大学 机械与车辆学院， 北京 100081)

0 引言

全电高机动平台是未来军事机动装备的重要研究发展方向，世界各国都在大力研发[1]。其中，串联式混合动力履带车辆由于其动力传动结构简单、系统可靠性高等优点而受到广泛关注。

能量管理策略作为混合动力核心技术之一，对履带车辆的动力性和燃油经济性具有显著影响。文献[2]针对履带式混合动力车辆提出了一种发动机负载功率跟随与电池组功率补偿的能量管理策略，实现了车辆机动性和燃油经济性的良好匹配。文献[3]基于随机动态规划策略进行履带车辆能量管理，采用策略迭代法求解以发动机转速、电池组荷电状态、车速和驾驶员功率需求为输入，发动机电子节气门为输出的最优控制策略，提高了车辆燃油经济性。近年来，基于模型预测控制的能量管理策略受到越来越多的关注[4-8]，该方法通过对未来工况的合理预测，使用优化方法对预测时域内的能量管理控制问题进行求解，实现能量管理的实时优化。但以上方法缺乏对越野路况的考虑，对于越野工况下履带车辆的能量管理存在一定的应用局限性。

本文以某混合动力履带装甲车辆为研究对象，在研究混合动力能量管理策略时，基于车速和姿态角建立越野路况识别模型，对不同越野路况下的履带车辆行驶速度进行预测；采用模型预测控制策略进行能量管理，合理分配动力电池与发动机- 发电机组的功率。研究结果表明，所提出的越野工况预测模型有利于改善工况预测效果，能量管理策略能够实现越野环境下履带车辆能量管理控制目标，有利于改善混合动力履带车辆性能。

1 越野工况预测方法

基于模型预测控制的能量管理策略需要对未来一段时间内的工况进行合理预测，体现了控制的前瞻性。本文通过分析和处理试验平台的历史行驶数据，考虑到不同越野路况下的车速变化特性，在进行工况预测时基于车载传感器采集车速和车辆姿态角等信息，利用支持向量机建立越野路况识别模型，对不同路况下的速度进行预测，预测结果作为能量管理控制的约束条件。

1.1 越野路况识别

支持向量机是路面不平度识别和地形辨识的常用方法[9-10]，本文利用车载传感器测量车速、车辆姿态角信息，在离线阶段基于支持向量机训练路况识别模型，实车使用时调用离线训练模型进行在线识别，算法流程图如图1所示。

图1 越野路况识别算法流程图Fig.1 Flow chart of cross-country road recognition algorithm

1.1.1 数据处理

作为一种有监督的机器学习算法，支持向量机需要对离线数据处理，进行数据标签化、分段和特征提取，为模型训练提供数据集。

1.1.1.1 数据标签化

数据处理的首要问题是数据标签化，即对典型越野路况进行分类。

在试验车辆的历史试验数据库中选取典型路况下的试验工况，速度曲线如图2所示，车辆在不同路况下的速度、加速度存在比较大的差异，因此将路况分为平坦、起伏和坡道3类，然后针对不同路况进行速度预测。

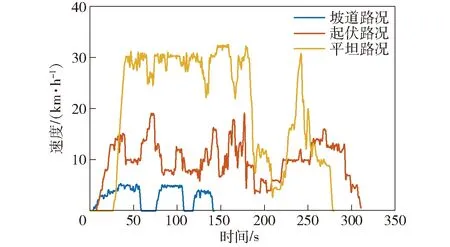
图2 典型越野路况下的试验速度工况Fig.2 Test speeds under typical off-road conditions

本文对不同路况下的道路负荷作一定的简化处理，仅考虑中低道路负荷的情况，根据文献[11-13]以及试验平台的历史试验数据，得出对应路况的道路阻力系数估计值如表1所示，典型越野路况下的俯仰角工况如图3所示。

图3 典型越野路况下的俯仰角工况Fig.3 Pitch angles under typical off-road conditions

典型越野路况道路阻力系数平坦0.09起伏0.16坡道0.21

1.1.1.2 数据分段与特征提取

数据分段是将循环工况的连续数据按一定的时间均分为相等长度的数据段，数据段时间的长短反映了路况识别的固有延迟时间。分别采用不同时间长度划分数据段，然后采用同样方法训练模型，再用同一组测试集进行测试，模型识别的准确度如表2所示。表2中显示以1 s划分数据段的模型准确度相对较高，又考虑到进行预测能量管理控制的控制周期一般为1 s，因此以1 s为时间长度划分数据段，在保证模型准确度的同时，使路况识别的更新时间与预测控制周期保持一致。

表2 数据分段时间比较

为了区别各个路况，需要对每个数据段内的数据进行处理，提取数据段内车速和车辆姿态角的统计特征，选取的特征参数如表3所示。

表3 特征提取

1.1.2 模型训练与在线识别

越野路况识别模型的建立过程就是利用支持向量机训练离线数据的过程。为了使模型具有较高的准确度，需要对支持向量机的核函数类型及其参数进行合理选择。常用核函数有线性、多项式型、径向基型和Sigmoid型4种，在其他条件相同情况下，分别使用4种核函数训练模型，模型识别的准确度如表4所示，通过对比分析，选择准确率更高、迭代次数更少的径向基类型函数作为核函数进行模型训练。

表4 核函数类型比较

支持向量机参数类型有惩罚因子C和核函数参数γ，将两个参数在[0.01,100]范围内进行对比选取，得出适合路况分类问题的参数选取方案，调参过程的部分曲线如图4所示，调参优化结果为C=1，γ=0.02.

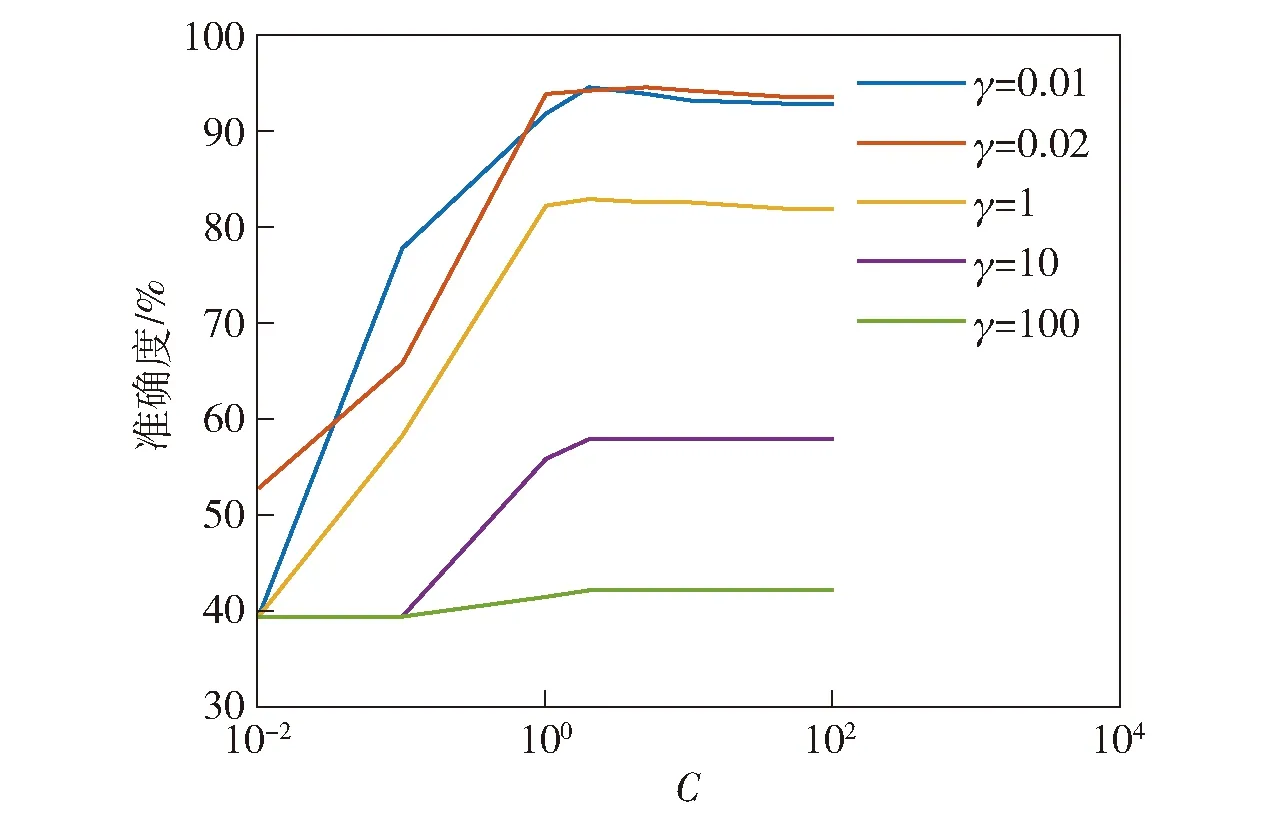
图4 模型调参曲线Fig.4 Parametric adjustment of model

将离线训练的模型保存至控制器，在线识别时，控制器接收传感器发送的车速、车辆姿态等信息后按表3提取特征，调用离线模型进行在线路况识别。

1.2 履带速度预测

车辆在行驶过程中，速度变化存在很大的不确定性。假设车辆加速度与历史状态无关，仅与当前状态有关，则可以将加速度变化视为马尔可夫过程，使用马尔可夫链进行速度预测[3]。履带车辆存在速差转向的运动特点，双侧电驱动履带车辆可通过控制两侧驱动电机实现任意半径转向。本文在进行速度预测时,分别计算不同路况下两侧履带速度的状态转移概率，单独预测每侧履带的速度。

将履带速度和加速度离散化，得到对应下标的速度值和加速度值：

v∈{v1,v2,…,vr};a∈{a1,a2,…,aq},

式中：r、q分别为速度和加速度最大索引下标。马尔可夫状态转移概率为

pij=P(a(n+1)=aj|v(n)=vi)，

(1)

式中：a(n+1)为第n+1时刻的加速度；v(n)为第n时刻的履带速度预测值；i、j分别为离散化的速度和加速度索引下标，i=1，2,…，r，j=1,2,…，q.

(1)式的含义为：当n时刻履带速度为vi时，n+1时刻加速度为aj的概率为pij.

对历史试验数据进行统计，计算状态转移概率pij为

(2)

式中：Ni,j为当前时刻速度为vi、下一时刻加速度为aj事件发生的次数；Ni为事件发生的总次数。

在离线阶段分别统计平坦、起伏和坡道路况的历史试验数据，分别得到各路况下的履带速度状态转移概率pij，平坦路况下左侧履带马尔可夫转移概率矩阵如图5所示。为使状态转移概率实时更新，引入修正系数λ，当前时刻为n时，若前一时刻发生了速度vi向加速度aj的转移事件，则对状态转移概率进行更新:

pij(n)=pij(n-1)+λ，

(3)

(4)

式中：s=1,2,…,q，s≠j.

图5 平坦路况下左侧履带的马尔可夫转移概率矩阵Fig.5 Markov transition probability matrix of left track on flat road

下一时刻履带速度预测值为

(5)

式中:v(n+1)为下一时刻的履带速度预测值；Δt为时间间隔。

预测时域内各个时刻的履带速度均可由上一时刻的预测值得到：

(6)

式中:k为预测时域内的目标时刻。

2 基于越野工况预测的能量管理策略

2.1 系统分析

本文研究的混合动力履带车辆采用串联式结构，如图6所示，双侧驱动电机通过减速机构带动两侧主动轮和履带转动，实现车辆的直驶和转向；发动机- 发电机组和动力电池组混合供电，车辆行驶的直接驱动力完全来自驱动电机，发动机动力不直接驱动车辆，实现了工作点的解耦。

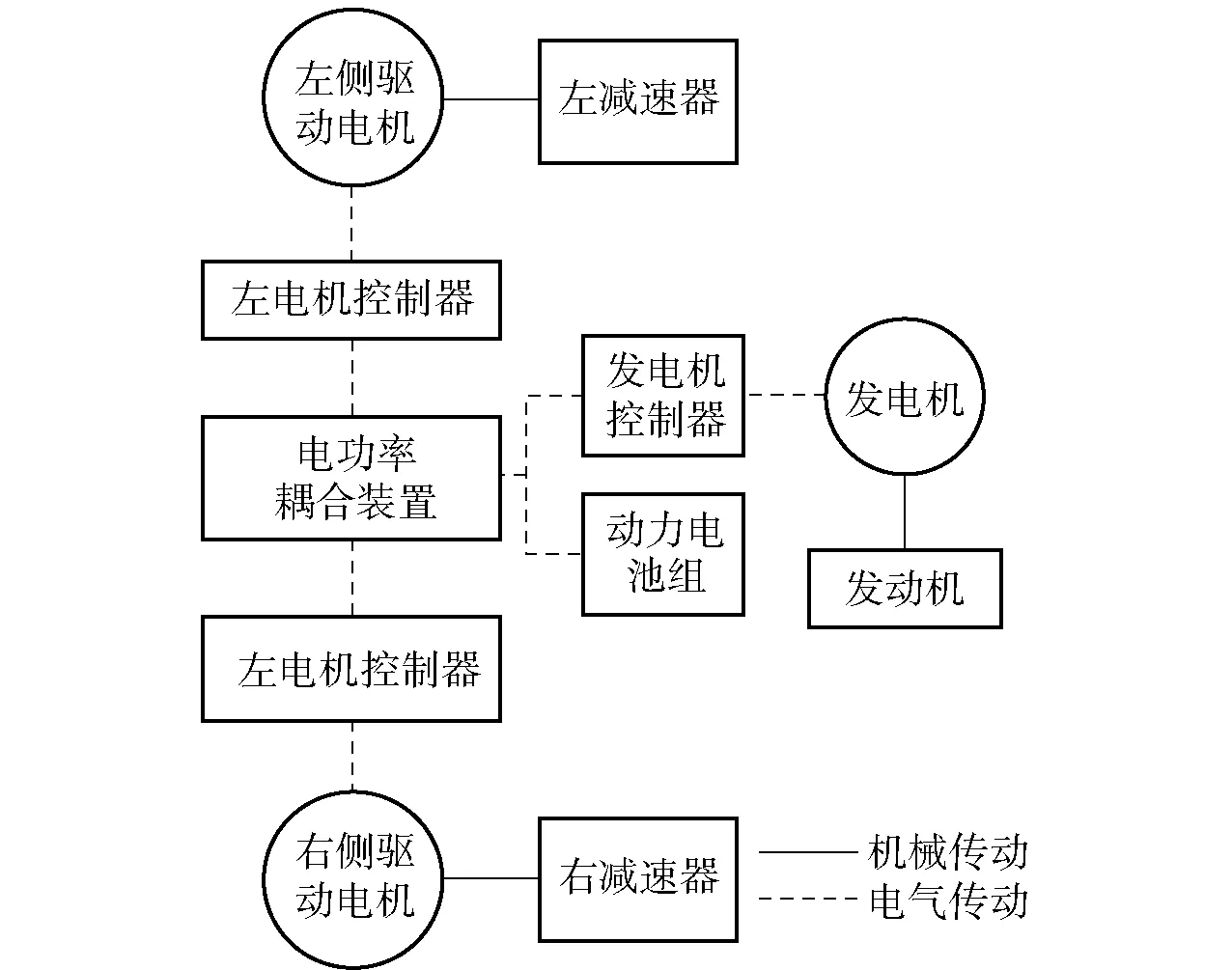
图6 混合动力传动系统原理图Fig.6 Schematic diagram of power transmission system for hybrid tracked vehicle

混合动力履带车辆能量管理的控制目标是在满足动力性功率需求和系统约束条件下，对发动机- 发电机组和动力电池组的功率进行合理分配，将动力电池组荷电状态(SOC)维持在一定的区间，并降低燃油消耗，提高燃油经济性。

2.2 面向能量管理的混合动力履带车辆建模

动力电池组是混合动力系统的关键部件，其SOC值对于能量管理控制起着至关重要的作用，使用等效电路模型对动力电池建模：

(7)

式中：Cb为电池额定容量；Vb为电池开路电压；Rb为电池内阻；Pb为电池功率。

系统选用具有电子调速功能的发动机，发动机采用转速控制方式，能量管理控制器通过CAN网向发动机控制器发送转速请求指令，根据台架试验建立的油耗特性图计算燃油消耗率：

(8)

式中：φf为根据台架试验数据确定的发动机油耗特性图查表函数；Te为发动机转矩；ne为发动机转速。

发动机输出轴与发电机输入轴刚性连接，二者的转速相等，发电机输出功率满足如下方程：

(9)

式中：ng和Tg分别为发电机输入轴转速和转矩；Je和Jg分别为发动机和发电机的转动惯量；Pg为发电机输出到直流母线的电功率；ηg为发电机效率。

发动机- 发电机组和动力电池组共同提供能量，满足整车功率需求，功率平衡方程为

(Pg+Pb)η=Pr，

(10)

式中：Pr为车辆需求功率；η为电功率转换效率。

混合动力履带车辆的功率需求来自于两部分，一是驱动系统的动力功率需求，二是冷却水泵等电气辅助设备的功率需求：

(11)

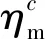
本文对履带车辆动力学进行一定简化，忽略履带的滑转、滑移，将履带车辆视为具有集中质量作平面运动的刚体，速差转向过程视为低速匀速运动，按(12)式计算履带车辆直驶和转向需求功率[8]：

(12)

式中：fd为道路阻力系数,由当前路况确定；m为车辆总质量；g为重力加速度；Ca为空气阻力系数；A为履带车辆的正面投影面积；ac为加速度；vc为车速；μ为转向阻力系数；L为履带接地长度；ω为转向角速度；vL、vR分别为左、右两侧履带速度；B为履带中心距。

2.3 基于越野工况预测的能量管理策略

模型预测控制是解决非线性、强约束问题的有力工具，其核心是通过对未来状态的合理预测，求解预测时域内的优化控制问题，但仅将最优控制序列中的第1个控制量作用于系统，然后重新开始下一个预测控制循环[14]。针对2.2节提出的混合动力履带车辆模型，根据越野工况预测结果利用模型预测控制策略进行能量管理，实时优化发动机发电机组和动力电池组的功率分配。对于混合动力履带车辆，能量管理的控制量为发动机转速ne和发电机转矩Tg，系统状态量为动力电池SOC，状态方程根据(6)式可写为

(13)

在每个采样时刻k、预测时域P内的能量管理优化函数为

(14)

能量管理控制系统在每个预测时域内需要满足如下物理约束：

(15)

式中：参数下标max和min分别为对应物理量的最大值和最小值。

能量管理算法流程图如图7所示，系统在每个采样时刻对当前状态进行更新，并对预测时域内的工况进行预测，构建能量管理优化问题；采用动态规划算法对预测时域内的能量管理优化问题进行在线求解，获得预测时域内的最优控制序列，将第1个控制量作用于系统，完成本次预测控制循环，并重新观测系统状态，开启下一个控制循环。

图7 能量管理算法流程图Fig.7 Flow chart of energy management algorithm

3 仿真实验结果与分析

本文基于某混合动力履带车辆实验平台，在前期大量实验数据的基础上，采用第2节方法训练了越野工况预测模型以进行预测能量管理。实验平台和典型实验路况如图8所示。为进一步分析越野工况预测效果和能量管理控制效果，验证本文提出的基于越野工况预测的能量管理策略的可行性与有效性，基于实车实验工况在MATLAB环境下进行了仿真实验。根据动力电池组的使用要求，混合动力模式下电池SOC最佳范围为0.6～0.8，因此将电池SOC初始值和目标值设置为0.7，仿真时长385 s，整车主要技术参数如表5所示。

图8 实验平台及典型路况Fig.8 Hybrid electric tracked vehicle and test road conditions

部件及整车参数数值最大功率/kW96发动机最大转矩/(N·m)313最高转速/(r·min-1)3200最大功率/kW90发电机最大转矩/(N·m)300最高转速/(r·min-1)3000总质量/kg7500整车履带中心距/m2.5主动轮半径/m0.2654

3.1 越野工况预测效果分析

仿真实验工况的俯仰角曲线如图9所示，实验工况的数据段共385个，路况识别正确的数据段为347个，准确度为90.16%. 错误分类多发生于将起伏路面识别为坡道路面，这是因为实验平台在起伏面上的部分行驶数据特征与坡道路面相似，从而出现少量误检。越野路况识别结果与实际路况对比如图10所示。

图9 仿真实验工况的车辆俯仰角Fig.9 Vehicle pitch curve under simulation test condition

图10 越野路况识别结果Fig.10 Recognition result of off-road condition

速度预测效果如图11所示，可见基于路况识别的速度预测可以较准确地对越野速度工况进行预测。为进一步表明预测效果，分别使用不同的预测方法进行预测，引入均方根误差作为评价指标，如(15)式所示，对不同的预测方法的预测效果进行对比。

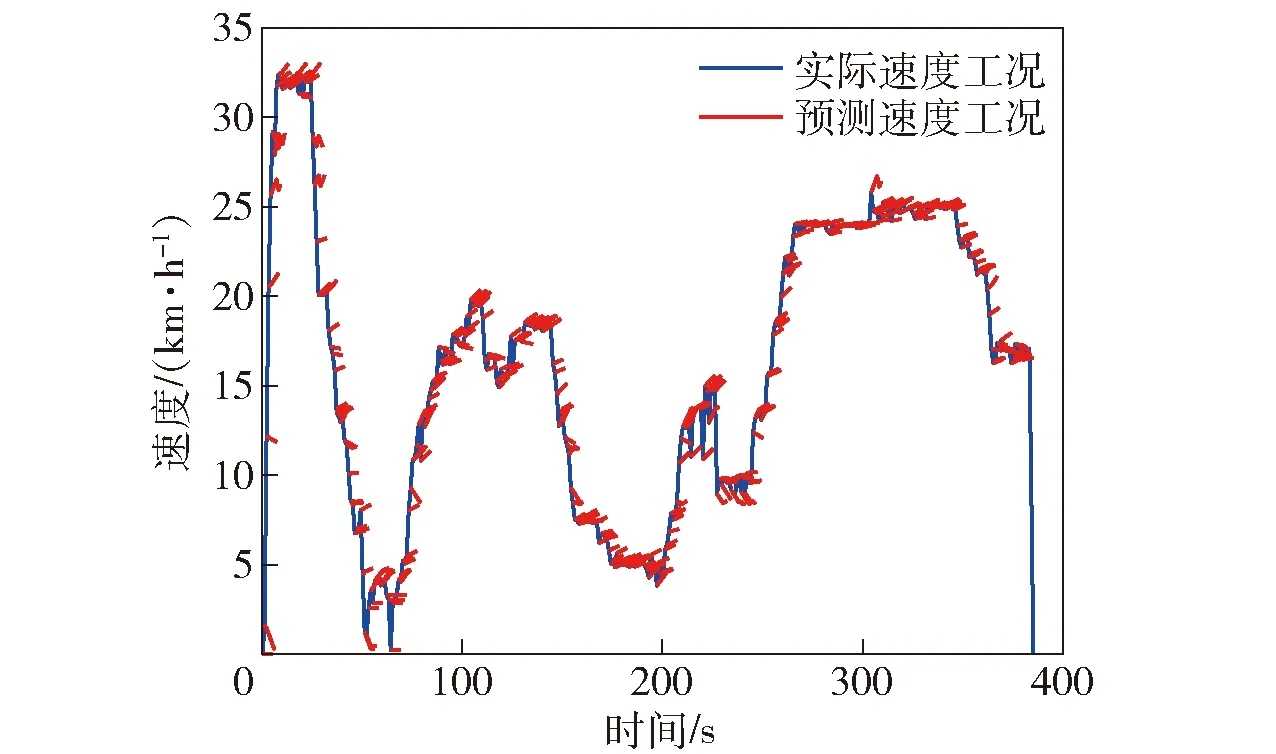
图11 速度预测结果Fig.11 Predicted speeds

(16)

式中：e为均方根误差；vp和vr分别为预测速度和实际速度。

表6显示了不同预测方法的预测结果，其中：维持预测是指将每一个预测时域内的速度均视为当前时刻的速度；马尔可夫预测是指将所有路况的速度工况进行统计，统一使用相同的转移概率进行预测；越野工况预测策略是指对路况进行区分，根据越野路况识别的结果分别对不同路况使用不同的转移概率进行预测，结果可见越野工况预测有利于提高预测的准确度，准确度提升约18.6%.

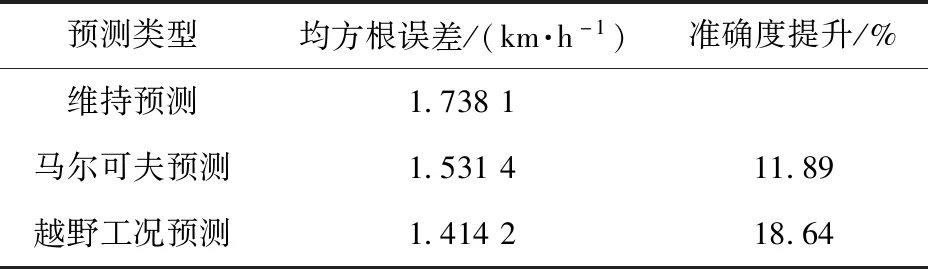
表6 速度预测效果对比

3.2 能量管理控制效果分析

基于越野工况预测结果和混合动力履带车辆模型，使用模型预测控制策略进行能量管理，电池SOC仿真结果如图12所示，在行驶工况中，能量管理策略在保证满足整车功率平衡的基础上，通过动力电池的充放电，调节发动机- 发电机组的输出功率以改善燃油经济性，同时能够将SOC维持在目标值范围附近，较好地完成能量管理的控制目标。

图12 电池SOC仿真曲线Fig.12 Simulation curve of battery SOC

为了比较不同控制策略在实验工况下的能量管理效果，分别采用基于规则的策略和基于越野工况预测的策略进行能量管理。图13比较了不同策略下发动机工作点的分布。由图13可见，与基于规则的控制策略相比，发动机有更多的工作点落在高效区内，工作范围得到改善。基于规则的策略下总油耗为993.5 g，而基于越野工况预测的策略下总油耗为920.1 g，燃油经济性提高了7.9%.

图13 不同策略下发动机工作点对比Fig.13 Comparison of engine operating points when using different control strategies

4 结论

本文针对越野环境下混合动力履带车辆能量管理问题，提出了一种基于越野工况预测的履带车辆能量管理策略。首先利用车速、车辆姿态角建立越野路况识别模型，然后基于马尔可夫链对预测时域内不同路况下的速度进行预测，最后建立混合动力履带车辆模型，以满足整车功率平衡和燃油消耗最小为目标，设计模型预测控制策略进行能量管理。

通过仿真实验，验证了越野工况预测策略有利于提高预测效果，预测准确度提升约19%，同时也验证了能量管理策略能够完成越野环境下履带车辆能量管理控制目标，有利于改善混合动力履带车辆性能, 与规则策略相比油耗降低约8%.