基于滚动时域的舰载机甲板运动轨迹跟踪最优控制

刘洁，韩维，徐卫国，刘纯，袁培龙，陈志刚，彭海军

1.海军航空大学，烟台 264001 2.陆军航空兵研究所，北京 101121 3.航空工业洪都650飞机设计研究所，南昌 330024 4.中国空气动力研究与发展中心，绵阳 621000 5.大连理工大学 工程力学系，大连 116024

舰载机在甲板上调运作业的效率和安全性，直接决定其出动效率，而舰载机的轨迹规划和跟踪是其中的关键环节。通常需要先对舰载机在甲板上的路径进行规划，而由于在路径规划过程中很难将外界扰动、初始偏差等因素考虑在内，所得出的路径一般均为理想情况下的可行路径。故在规划出舰载机的运动轨迹之后，还需要考虑实际环境中的外界扰动、初始偏差等因素，使舰载机的实际运动轨迹和理想轨迹之间的偏差尽可能的小，从而可以尽量按照预定的理想轨迹进行运动，即以较高的精度实现对理想轨迹的跟踪。然而，对于舰载机在甲板上的运动轨迹跟踪问题还鲜有研究，为此本文将对这一问题进行深入研究。

舰载机在甲板上运动的轨迹跟踪问题是通过设计合理的跟踪方法，并结合其运动学/动力学方程以及相关约束关系，对理想轨迹进行跟踪。目前，对于舰载机在甲板上运动的轨迹跟踪问题，国内外鲜有研究。而在其他领域，无人地面系统(UGS)，包括无人飞行器(UAV)和机器人的轨迹跟踪被广泛研究，因此可借鉴这些领域内的跟踪方法和理论对舰载机在甲板上运动的轨迹跟踪问题进行研究[1-2]。然而，轨迹跟踪问题中仍存在以下难点和重点：① 系统的非线性和耦合特性；② 控 制输入和输出的物理约束；③ 环境不确定性的影响[3-4]。目前常用的跟踪控制方法可分为五大类：几何和运动学跟踪控制方法、经典跟踪控制方法、基于动态状态反馈(线性和非线性)的跟踪控制方法、模型预测(MPC)方法、基于神经网络和模糊逻辑的跟踪方法。

几何和运动学控制方法主要被用于车辆的轨迹跟踪领域，这类方法易于实现，但仅适用于不需要考虑系统动力学的情况，它主要包括Pure-pursuit和Stanley这两种方法。Pure-pursuit是通过在运动体前方构建虚拟点，并对虚拟点进行跟踪的方法[5-6]；Stanley是通过考虑纵向和横向误差，来计算转向角需要修正的角度[7-8]，采用这类控制器很难权衡稳定性与跟踪性能之间的关系。基于运动学的控制方法是根据系统运动学(如纵向速度、横向速度、偏航率等)设计反馈控制器，它可改善几何控制器的跟踪性能。但是，由于这些方法没有考虑系统的动力学，因此不能保证它们在高速运动环境中仍具有很好的适用性。

经典控制方法主要包括比例-积分-微分(PID)控制和滑模控制。PID控制器原理简单，是工业上常用的控制器，通常由实际响应和期望响应之间的误差来进行触发。采用经典PID技术的跟踪控制器具有良好的跟踪性能，但由于系统运动学或者动力学的非线性特点，使得控制效果对控制器参数非常敏感。如李林琛[9]和冯剑[10]等采用PID控制理论，对机器人的路径跟踪问题进行了研究。Pan等[11]等提出了一种线性PID控制器，用于柔性执行机构驱动机器人的跟踪控制。Zhu等[12]提出了一种PID反馈控制方法，并将其应用于微自主飞行器的横向控制中，实现了轨迹跟踪。针对移动机器人的轨迹跟踪问题，Normey-rico等[13]采用一个由积分器和延时器组成的简单线性化移动机器人跟踪模型。而滑模控制(SMC)是一种成熟的非线性状态反馈控制器，采用滑模控制器得到的控制律具有良好的跟踪精度[14-16]。如Asif等[17]利用自适应滑模控制理论提出了一种输出反馈控制方法，并对观测器的稳定性进行了分析。Elmokadem等[18]针对水下机器人的跟踪控制问题，采用滑模控制技术提出了一种轨迹跟踪控制方案，可有效抑制外界扰动。Yang和Kim[19]基于滑模理论，提出了一种渐近稳定的滑模控制律，对有界外部扰动具有较强的鲁棒性。靳永强[20]和丛炳龙等[21]采用滑模控制理论，对航天器姿态跟踪问题进行了研究。Ouyang等[22]针对机器人系统的轨迹跟踪控制问题，基于滑模控制和PD控制，提出了一种PD-SMC方法，该方法采用PD控制来稳定被控系统，同时采用SMC来补偿扰动和不确定项，从而可以较好的抑制跟踪误差。Boukattaya等[23]提出了一种鲁棒自适应非奇异快速末端滑模(NFTSM)跟踪控制方案，可有效抑制有界外部扰动。这些方法可有效解决特定的问题，但也存在一些缺点，即① 跟踪控制性能对控制器采样率敏感；② 存 在抖振；③ 仅在滑动面上具有鲁棒性；④ 需要扰动和不确定性干扰的先验知识。

基于动态状态反馈(线性和非线性)的控制方法在考虑系统动力学或者运动学的同时，具有比几何控制器更好的控制性能[24]。基于线性二次调节器(LQR)的控制律设计简单，但在跟踪曲率变化较大的轨迹时，需要前馈控制来实现无误差跟踪，然而添加前馈控制会使得跟踪控制器对参考轨迹中的不连续点敏感[25]。另一方面，基于最优控制的方法虽然在高速运动下也能实现精确的轨迹跟踪，但这只有在某些假设(如在优化阶段的速度保持不变)得到满足时才能实现。近年来，非线性自适应控制技术，如Inversion &Immersion (I&I)也被用于轨迹跟踪控制领域。初步研究表明，该方法具有鲁棒的闭环跟踪性能，但控制器对参数的不确定性敏感[26]。同时，Tagne等[26]还提出了一种具有非线性增益的轨迹跟踪自适应比例积分(PI)控制器。仿真结果表明，该控制器具有与SMC和I&I控制器相当的跟踪性能，并且对参数不敏感。然而，在存在较大曲率变化的情况下，或在系统动力学非线性区域运行时，控制器的增益有增大的趋势，可能对执行机构产生不利影响。

此外，为了对标准轨迹进行跟踪，通常是采用线性化方法将原来的非线性系统转化为线性时变/时不变系统，并基于线性控制理论设计控制器以实现跟踪。Falcone等[27-29]对非线性车辆模型实时的进行线性化，进而提出了模型预测控制方法。Kühne等[30]利用线性MPC对轮式移动机器人的误差模型进行线性化，提出了具有非完整约束的(WMR)的最优控制策略。Bahadorian等[31-32]将移动机器人的非线性跟踪误差模型线性化，提出了一种鲁棒模型预测控制器(RMPC)来进行轨迹跟踪控制。Gutjahr等[33]将自主车辆的制导描述为具有约束条件的最优控制问题，并采用线性时变MPC方法提出了横向制导策略。Plessen和Bemporad[34]基于闭环跟踪控制理论，设计了一种线性时变预测控制方法 。Li等[35]提出了一种基于神经动力学优化的MPC方法来实现非完整移动机器人的轨迹跟踪。Ali等[36]将机器人的非线性行为线性化，设计了一种基于模糊逻辑理论、极点配置的混合控制器。张万枝等[37]将农业车辆非线性运动学模型线性化，建立了控制控器预测方程，对车辆导航路径自动跟踪问题进行了研究。对复杂非线性系统进行一阶泰勒展开从而获得线性模型的方法，可将问题简单化，具有明显的优点，且有较为成熟的线性控制理论作为支撑，可实现快速的求解[38]。然而，由于这种方法常常忽略了高阶项，当误差或扰动较大时，线性化模型可能难以描述原系统的某些特征。随着计算机技术的不断发展，一些研究者试图采用非线性理论和数值计算理论来解决这一问题。例如，Ostafew等[39]提出了一种基于学习的非线性MPC方法，将扰动描述为高斯过程，实现了对移动机器人的轨迹控制。刘昌鑫等[40]采用非线性MPC理论，对设计了欠驱动AUV的路径跟踪问题进行了研究。Yang等[41]基于极限学习机理论和混沌优化算法，设计了一种非线性预测控制策略，解决了存在外部干扰情况下的跟踪控制问题。非线性MPC可以实现非常精确的跟踪，但同时由于计算量比较大，难以实现在线的跟踪控制。Carvalho等[42]提出了一种基于非线性模型迭代线性化的MPC框架，设计了一种扩展线性MPC控制器，并进行了实验验证，这种方法有助于实现计算效率和精度之间的折衷。

由于神经网络和模糊逻辑控制具有指导控制器进行快速决策的能力，因此在许多自适应和智能控制中都有应用[43-47]。如刘芳等[48]采用自适应深度网络对无人机的目标跟踪问题进行了研究。高鸣等[49]采用模糊逻辑理论设计了一种智能控制器，可对预设轨迹进行较好的跟踪。利用这两种方法实现的决策算法可以分为监控型和普通型控制器型两种，对于监控型控制器，决策算法被用来优化主控制器中选定的参数，而主控控制器又可以被视为自适应控制器；对于普通型控制器，决策算法将被作为主控制器以确定系统的控制输入[50]。虽然自适应/智能控制器可提供一个鲁棒性的解决方案，但神经网络或模糊系统应该具备“专业知识”或“经验”来做出正确的决定。因此，智能控制器中的算法需要用大量的先验信息进行学习、训练，从而不断学习和获得更多的“专业知识”，才可能根据实际情况来做出正确的反应。然而，在缺乏正式的稳定性证明和异常处理的情况下，这些方法还不能很好的被应用于实际装备或者设备中[51]。

由于每个研究人员都是在一个独特的环境下演示或者验证自己提出的跟踪控制器，因此很难对文献中提出的不同控制器进行直接比较。然而，Rupp和Stolz[52]设计了5种不同的轨迹跟踪控制器(Stanley、LQR、SMC、Fuzzy和MPC)来模拟120 km/h的超车操纵。由于它们均被应用于相同的系统，可更加科学的、直接的比较不同控制算法。通过初步比较的结果表明：采用MPC方法得到的跟踪误差最小，转向角最平稳。

对于单架舰载机在甲板上滑行的轨迹跟踪控制问题，飞机的运动特性与无人车或者机器人的运动属性相类似，因此可结合飞机在甲板上滑行的运动学/动力学特性，并借鉴上述方法来实现其轨迹的跟踪控制。

对于牵引飞机系统在甲板上的轨迹跟踪，几乎没有关于的相关文献。在一定程度上，它可以被视为是一种拖-拉系统，因此可以参考拖-拉系统跟踪问题的控制策略。基于线性化模型的线性控制技术已广泛应用于拖-拉系统的控制[53-55]。然而，如果航向角大于10°，线性化模型的精度就会降低[56]。为了提高精度，一些研究采用了用非线性控制理论来研究拖-拉系统，包括横向函数法[57]、虚拟转向法[58]、非线性模型预测控制[59]和李雅普诺夫方法[60-62]。

根据牵引系统的结构特点，可将飞机视为拖车，主要目标是跟踪飞机的轨迹，使飞机可以尽可能的按照理想轨迹到达预定位置，而牵引车的状态不是研究的重点，它的状态可以根据系统的干扰进行调整。然而，在上述研究中，牵引车通常被视为激励源，研究的重点大部分集中在对牵引车的跟踪。此外，大部分跟踪算法均只能解决系统的倒车或者正向行驶问题，而对于给定的参考轨迹，尤其是既涉及倒车又涉及正向行驶的参考轨迹，其跟踪问题都没有很好地得到解决。这主要是因为牵引系统的运动学或者动力学模型较为复杂，对于正向运动与倒车之前切换的过程很容易发散，现有的方法难以有效解决这一过程的轨迹跟踪问题。

1 舰载机轨迹运动学模型的建立

舰载机在甲板上的调运方式主要分为3种：自主滑行、无杆牵引、有杆牵引。其中，自主滑行和有杆牵引这两种方式主要用于航母舰面的飞机调运，无杆牵引这种方式主要用于机库内的飞机调运。如在舰载机的出动环节中，需要飞机从停机位自主滑行到对应的起飞位；而由于飞机无法自主实现倒车等动作，因此当飞机需要在不同停机位之间转换或者回收时，通常需要借助牵引车来实现飞机的倒车，即采用有杆牵引的调运方式；而在飞机出库(从机库内的停机位调运至升降机位置)或者从升降机调运至停机位时，通常是采用无杆牵引的调运方式。

由于牵引车的作用，采用牵引车牵引的调运方式较飞机自主滑行而言，使飞机的运动功能得到了丰富，飞机既可实现正向运动也可实现倒车运动，但随着牵引车(或牵引杆)等连接结构的引入，使得系统变得更加复杂。且由于这3种调运方式所对应系统不一样，其运动学规律和控制规律也存在着差异，因此有必要对这3种系统分别进行研究。

1.1 舰载机滑行运动学模型

当舰载机在甲板上运动时，它的运动机制可概括为：由发动机提供加速度从而使舰载机向前运动，通过前轮的转角来进行方向控制。假设舰载机在甲板上的运动只产生滚动摩擦，而不发生滑动，则无需分析其水平推力、摩擦力或惯性特性即可对其运动进行分析，其运动约束为一个非完整的运动约束[63]，运动关系如图1所示。

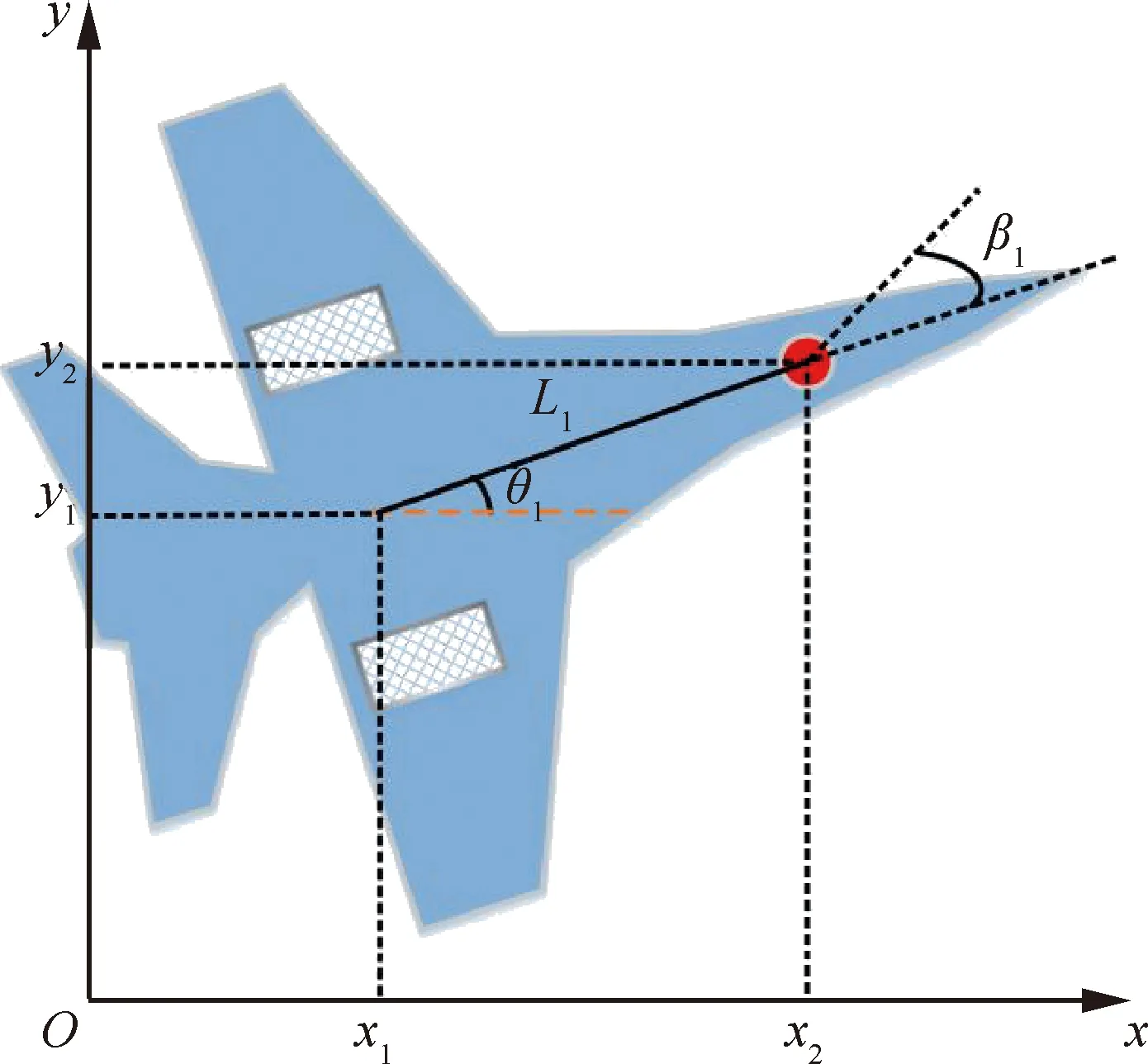
图1 舰载机轮廓图Fig.1 Profile of carrier-based aircraft

图中：L1为沿舰载机轴线方向上，前轮与后轮之间的垂直距离；方向变量θ1为舰载机轴线与横坐标的夹角；β1为前轮的转向角。

则其运动学方程可表示为

(1)

式中：状态变量X由两个位置坐标[x1，y1]、方向变量θ1组成；控制变量U=[u1，u2]T，且u1为前轮的转向角β1,u2为飞机的平移速度v1。

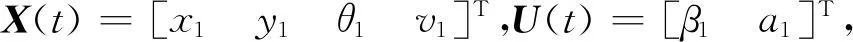
(2)

为了简化计算，本文将基于式(2)，将控制变量构造为：U(t)=[u1u2]T，且u1=tanβ1,u2=a1。通过求解控制变量U(t)，再结合β1=arctanu1，即可实现对飞机转向角和加速度的求解。由式(2)可进一步表示为

(3)

边界条件为X(t0)和X(tf)。

1.2 无杆牵引系统的运动学模型

根据Karkee的结论，当系统的速度较小时(小于4.5 m/s)，运动学模型可以较好的描述带拖车系统的运动[64]。由于无牵引车的舰载机系统与带拖车系统的结构类似，因此该无杆牵引系统也可被视为一个带拖车系统。在不考虑系统的横向推力、摩擦或者惯性等因素的前提下，可将其运动关系进行简化，具体如图2所示。

图中：θ1和θ2分别为舰载机和牵引车的轴向与横坐标之间的夹角；x1和y1分别为被牵引飞机的横纵坐标；β2为牵引车的转向角；L2为牵引车的前后轮距；L1为飞机的前后轮距；M0为飞机与牵引车铰接点与牵引车后轮之间的垂直距离。

当M0=0 m时，表示该铰接点在牵引车两个后轮之间，则该系统为轴上牵引系统；反之，系统为离轴牵引系统。为了不失一般性，本文将针对离轴牵引系统进行建模。

与舰载机滑行不同，无杆牵引系统的运动主要是由牵引车来提供，飞机在牵引车的驱动下，可以实现正向运动以及倒车运动，整个系统的控制核心系于牵引车，为此系统的控制变量主要是由牵引车的加速度以及转向角组成。与舰载机滑行运动学模型类似，为了描述起始位置和终端位置处的速度约束，本文将速度变量引入到状态变量中，且牵引系统最终的目标是将飞机调运到指定位置。为此，其状态变量主要包括飞机的位置、角度以及牵引车的角度θ2以及速度v2。则根据系统的结构关系以及运动关系，可得到其运动学方程为

图2 无杆牵引飞机系统的运动关系图Fig.2 Off-axle hitching towed aircraft system without drawbar

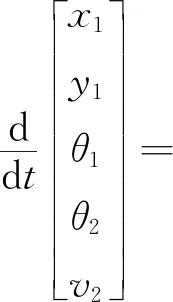
(4)

1.3 有杆牵引系统的运动学模型

目前，在航母上使用的有杆牵引系统一般均为离轴系统，其结构如图3所示。

图3 有杆牵引系统组成示意图Fig.3 Off-axle hitching towed aircraft system with drawbar

图中：θ1、θ2以及θ3分别为飞机、牵引杆以及牵引车的方向角；[x1，y1]、[x2，y2]、[x3，y3]以及[x4，y4]分别为飞机、飞机与牵引杆铰接点、牵引杆与牵引车铰接点以及牵引车的位置坐标；β1、β2以及α分别为飞机、牵引杆和牵引车的转向角；L1为飞机前后轮距；L2为牵引杆的长度；M为牵引杆与牵引车铰接点到牵引车后轮的垂直距离；L3为牵引车前后轮的距离。飞机和牵引车的速度分别为v1和v3，根据系统的结构设计和使用规定，飞机和牵引车的速度、转向角均应被约束在一定范围内。

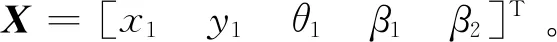
且由于飞机与牵引车的速度可以表示为

(5)

(6)

式中：Δ=cosβ1cosβ2(L3+Mu1tanβ2)注：该方程的建立是基于所有的转向角均小于55°，且M≤0.5L3，基于该假设，可使得cosβ1cosβ2(L3+Mu1tanβ2)≠0，且cosβ1≠0，cosβ2≠0。根据当前主流的相关设备，这一假设可适用于大部分拖-拉系统。

2 连续非线性舰载机系统的轨迹跟踪模型及最优控制条件

2.1 连续非线性舰载机系统的轨迹跟踪模型

对于跟踪控制问题的研究，一般均是基于跟踪误差模型或者伺服跟踪控制模型，由于舰载机系统的运动学系统(包括舰载机滑行、无杆牵引系统、有杆牵引系统的运动学模型)均为非线性系统，难以推导出其跟踪误差模型。因此，本文将采用伺服跟踪控制模型来进行研究。

为了更好对标准轨迹进行跟踪，在满足飞机系统的运动学约束、控制变量约束和状态变量约束条件下，需使跟踪误差应尽可能小。此外，还需使控制变量尽可能的平稳，即使能量尽可能的小，以利于工程实际应用。因此，轨迹跟踪问题可以表示为

(7)

式中：Xr为标准轨迹；X为实际的轨迹(系统的状态变量)；U为实际的控制变量；P为半正定的对角矩阵；R为正定的对角矩阵；h≤0表示相应的状态和控制约束。

研究目标为单机滑行的轨迹跟踪时，f(X(·)，U(·),t)为式(3)；研究目标为无杆牵引系统的轨迹跟踪时，f(X(·),U(·)，t)为式(4)；研究目标为有杆牵引系统的轨迹跟踪时，f(X(·)，U(·)，t)为式(6)。

不论舰载机滑行、无杆牵引系统、有杆牵引系统，本文关注的重点都是舰载机的位置和姿态，即主要是对舰载机的横纵坐标以及角度进行跟踪。故可通过对P矩阵进行设置来可满足这一条件，即将舰载机的横纵坐标以及角度对应的权重设为较大的值，以确保将横纵坐标以及角度误差可以被有效的抑制。

2.2 连续非线性舰载机系统的轨迹跟踪最优控制条件

由于单机滑行、无杆牵引系统、有杆牵引系统的运动学方程均是非线性耦合系统，很难直接求解。因此，可采用拟线性化方法来解决所建立的带约束连续非线性舰载机系统的轨迹跟踪最优控制问题。通过拟线性化处理，可将非线性最优控制问题转化为一系列线性二次最优控制问题。在不失一般性的前提下，式(7)可以表示为

(8)

式中：k=0,1,2,…；(·)[k]表示在第k次的迭代中(·)的结果。目标函数及约束中相关矩阵的具体表达形式为

W[k+1]=W[k]+(X[k+1]-X[k])TE[k]+

(U[k+1]-U[k])TF[k]+

(U[k+1]-U[k])TQ[k](X[k+1]-X[k])+

(9)

(10)

(11)

(12)

(13)

式中：第k次迭代的结果将作为第k+1次迭代的参考解。为表示方便，下文将不再用上标来表示，而是采用(*)pre来表示前一次迭代的结果。

通过引入非负补偿向量α，使得

CX+DU+V+α=0

(14)

进而可引入Lagrange算子λ和参数乘子向量β，使得原问题变为无约束最优控制问题，且参数乘子向量满足αTβ=0，β≥0，α≥0。则目标函数可表示为

(15)

且Hamiltonian函数为

H=W+λT(AX+BU+W)+

βT(CX+DU+V+α)

根据经典变分法，若使目标函数J最小，则需要使系统同时满足控制方程、Hamiltonian正则方程和终端的横截条件。其中，控制方程为

则可到

U=Upre-R-1(F+Q(X-Xpre)+BTλ+DTβ)

(16)

进一步可得到

(17)

而Hamiltonian正则方程可表示为

(18)

因此，可将原问题转化为两点边值与线性互补(LCP)的耦合问题。

由于在跟踪问题中，终端时间均是固定的，当终端的状态变量为自由时，则根据终端的横截条件，对应的Lagrange算子应为0；反之，在终端的状态变量则应为给定的X(tf)。

3 基于滚动时域的在线跟踪最优控制算法

3.1 全状态的保辛伪谱法

本文所建立的连续非线性舰载机系统的轨迹跟踪最优控制模型可被视为一个带约束的最优控制模型，常用能量最优型或者时间-能量最优型目标函数的被积分项中均为状态变量和控制变量的标准二次型，而所提出的最优跟踪目标函数中引入了标准轨迹所对应的常数项。因此，本节将根据第三类生成函数以及跟踪模型中目标函数的不同，提出全状态保辛伪谱算法。

全状态保辛伪谱算法的第1步是采用LGL伪谱法对X、λ、β和α这4个自变量进行近似化处理，具体的步骤可参照文献[65-66]。

在单个区间内，根据第三类生成函数的稳态条件，由两点边值问题以及起始和终端的边界条件，可得

Kjσj+ξjβj+γj=rj

式中：j表示在第j个区间内；Kj、ξj和γj的具体表达式为

由控制方程可将边界约束等式进行进一步整理成：

(19)

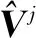
式中：

进一步可将式(19)整理为

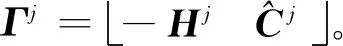
最后，再采用文献[65-66]中的方法对整个区间进行求解，得到最优解。

为了提高所提出方法的计算效率，本文将初始猜测解设为

1)当终端状态固定时，状态变量的初始猜测解由初始状态和终端状态进行插值而得到；当终端状态自由时，将状态变量的初始猜测解设为初始状态。

2)将控制变量的初始猜测解设置为控制变量的上限。

3)将Lagrange算子的初始猜测解设置为1。

则全状态保辛伪谱算法的步骤可总结如下：

1)设置各个区间内的LGL配点个数，以及收敛条件ε。

2)设置初始猜测解X[0]、U[0]、λ[0]，并对时间区间进行离散化处理。

3)对自变量X、λ、β以及α进行近似化处理。

4)在单个区间内采用基于第三类生成函数的全状态保辛伪谱算法。

5)将整个区间的对矩阵进行组装，并结合边值条件对相应的矩阵进行修改。

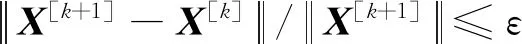
3.2 时间窗口边界条件的确定

本文基于滚动时间窗口理论，将整个时间区间上的最优跟踪控制问题转化到不同小时间区间(时间窗)内的最优控制问题进行求解。通过对每一个时间窗口内的最优跟踪控制问题进行求解，并不断向前滑动时间窗口，即可实现对标准轨迹的在线跟踪。根据最优控制模型，需要确定系统在起始和终端时刻的边界条件，即需要确定每一个时间窗口左侧的起始状态变量和右侧的终端状态变量。

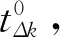
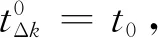
除此之外，也可将窗口右侧的边界条件设为自由。这样处理是因为在目标函数中已将偏差考虑在内，所以在计算时为了得到较小的目标函数值，也会尽可能的缩小与标准轨迹之间的误差，但这种处理方法无法确保在窗口右侧的误差为0。这两种处理方式可视具体要求和问题进行采用。

3.3 基于滚动时域的在线跟踪最优控制方法求解框架

根据以上思路，基于滚动时域(RHC)的在线跟踪最优控制方法的具体计算步骤可以概括为：

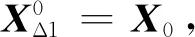
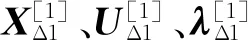
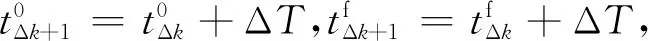
3.4 算法的保辛证明

由于所提出的在线跟踪最优控制算法是将本文提出的全状态保辛伪谱法应用到每一个滚动时间窗口内，因此只要证明了所提出的全状态保辛伪谱法是保辛的，即能说明在线跟踪最优控制算法也是保辛的。

对于采用基于第三类生成函数的全状态保辛伪谱法所得到相邻两个时间区间内的解soluj=[Xjλj]T和soluj-1=[Xj-1λj-1]T，假设存在如下映射关系：

soluj=Ψ(soluj-1)

(20)

若转移矩阵的Jacobi矩阵是辛矩阵，则说明本文提出的全状态保辛伪谱法是保辛的[67-68]，其中转移矩阵的Jacobi矩阵可表示为

(21)

根据辛理论，若上述的Jacobi矩阵为辛矩阵，则应该满足如下关系：

JTTSJT=S

(22)

式中：单位辛矩阵S为

(23)

进而，由式(21)和式(22)可得到：

(24)

(25)

(26)

若上述3个方程得到了满足，则说明本文提出的算法是保辛的。

定理1对于式(7)中描述的连续非线性舰载机系统轨迹跟踪模型，基于滚动时域的在线跟踪最优控制求解算法是保辛的。

证明：由于所提出的在线跟踪最优控制算法将本文提出的全状态保辛伪谱法应用到每一个滚动时间窗口内，而全状态保辛伪谱法是基于第三类生成函数所提出的，若所提出的全状态保辛伪谱法是保辛的，则基于滚动时域的在线跟踪最优控制算法是保辛的。

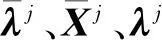
对Xj-1求偏导数，并结合链式求导法则，则可得到

(27)

将式(27)进一步整理可得

(28)

式中：

对λj-1求偏导数，并结合链式求导法则，则可得到

(29)

将式(29)进一步整理可得

(30)

式中：

由式(30)进一步可得

(31)

此外，由式(30)可得

(32)

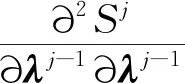
由式(30)还可得

(33)

结合式(28)，可得到

(34)

则

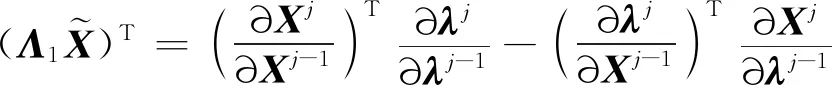
(35)

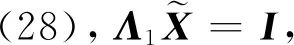
(36)

进而可证明式(26)是正确的。

通过以上讨论，式(24)、式(25)以及式(26)均得到满足。因此，基于第三类生成函数所提出的全状态保辛伪谱法是保辛的，则基于全状态保辛伪谱法以及滚动时域所提出的在线跟踪最优控制算法也是保辛的。

由于本文提出的算法是保辛的，则根据算法得出的结果可保留原连续哈密顿系统的辛属性，结果的精度更高，且所得的跟踪结果满足最优控制条件，可从理论上确保所得到的结果是最优的。

4 单机滑行的轨迹跟踪控制

4.1 存在初始偏差

为了验证本文所提出的在线跟踪的准确性和实时性，本文选取图4中绿线所示的滑行轨迹作为标准轨迹。

根据所提出的连续非线性舰载机系统的轨迹跟踪模型，以及舰载机滑行的运动学方程和相关的约束关系，采用本文所提出的在线跟踪最优控制算法，可实现对舰载机滑行的轨迹跟踪。

根据舰载机在甲板上滑行的安全规定，其滑行速度应该满足相应的约束，即0 m/s≤v1≤1.5 m/s；飞机的转向角也应满足其结构约束，|u1|≤1.5；飞机的加速度应不大于2 m/s2，即|u2|≤2 m/s2。由于实际轨迹与标准轨迹不可能完全重合，实际轨迹和标准轨迹之间的偏差是不可避免的。为此，在进行轨迹规划时，一般会增加一个缓冲区(扩大障碍物的实际轮廓线)。若实际的轨迹和标准轨迹之间的偏差在缓冲范围内，则说明实际轨迹没有与障碍物发生碰撞；反之，则说明实际轨迹与障碍物之间发生了碰撞。所以，实际的轨迹还应满足如下关系：

(x1-x1r)2+(y1-y1r)2≤dist2

(37)

式中：x1r和y1r为标准轨迹对应的横纵坐标点；dist为缓冲距离，本文取dist=1 m。

为此，舰载机的轨迹跟踪问题为一个状态变量和控制变量约束的跟踪控制问题。

由于目标函数中的权重矩阵反映了各个变量的重要程度，而不同的权重也会引起不同的结果。为研究不同的权重系数对跟踪效果的影响，以便选取合适的权重系数进行下一步研究，本文将R=diag(R1,R2)设置为单位矩阵，并采取不同的权重系数P=diag(P1,P2,P3,P4)来进行仿真实验。而跟踪的主要目标是为了保证舰载机按照预定的轨迹运动，所以主要的观测指标为舰载机的位置以及角度。此外，无杆牵引系统的初始偏差分别设为Δx1=0.5 m、Δy1=-0.5 m、Δθ1=0.05、Δv1=0 m/s，则P矩阵的取值可见表1。

将滚动窗口的步长设置为2 s，每个时间窗口内分为3大段，每一大段又分为3个小段，共计10个配点，滚动步长为0.2 s，在线跟踪算法的收敛精度为1×10-4。分别采用不同的权重系数进行仿真实验，具体结果如图5所示。

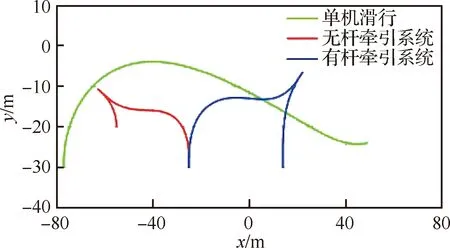
图4 标准轨迹Fig.4 Standard trajectory

表1 单机滑行中不同权重系数Table 1 Different weight coefficients for singlecarrier-based aircraft system

图5 不同权重系数情况下的单机滑行轨迹跟踪误差Fig.5 Tracking errors with different weight coefficientsfor single carrier-based aircraft system

图5为在不同的权重系数下，3个状态变量的误差随时间的变化关系。由图5可分析出，Case 1比Case 2～4对应的调节时间长、超调量小；对于Case 2～4，其调节时间和超调量均很接近。这主要是因为随着权重系数的增加，即状态变量的重要性相对控制变量越来越大时，为了抑制误差以确保跟踪目标函数数值尽可能的小，系统会尽可能在较短的时间内去调节误差，因此误差的变化将更加剧烈，超调量会增大，调节时间会变小。但当权重系数达到一定程度时，由权重系数的增大所引起的变化将越来越小。

此外，在考虑误差的抑制情况时，还需考虑控制的平稳性，为了研究不同权重系数对控制平稳性的影响，本文给出了对应的控制变量，具体如图6所示。由图6可分析出，Case 1对应的控制变量最平稳，其次为Case 2对应的控制变量，Case 3和Case 4对应的控制变量变化均较为剧烈。这主要是因为随着权重系数的增加，即状态变量的重要性相对控制变量越来越大时，为了抑制误差以确保跟踪目标函数数值尽可能的小，跟踪系统会尽可能在较短的时间内去调节误差，因此需要更快、更大幅度地去调节控制变量，以达到修正误差的目的，则控制变量的平滑度将变差。为了平衡误差的变化和控制变量的变化，本文将P矩阵的取值设置为1×103量级。

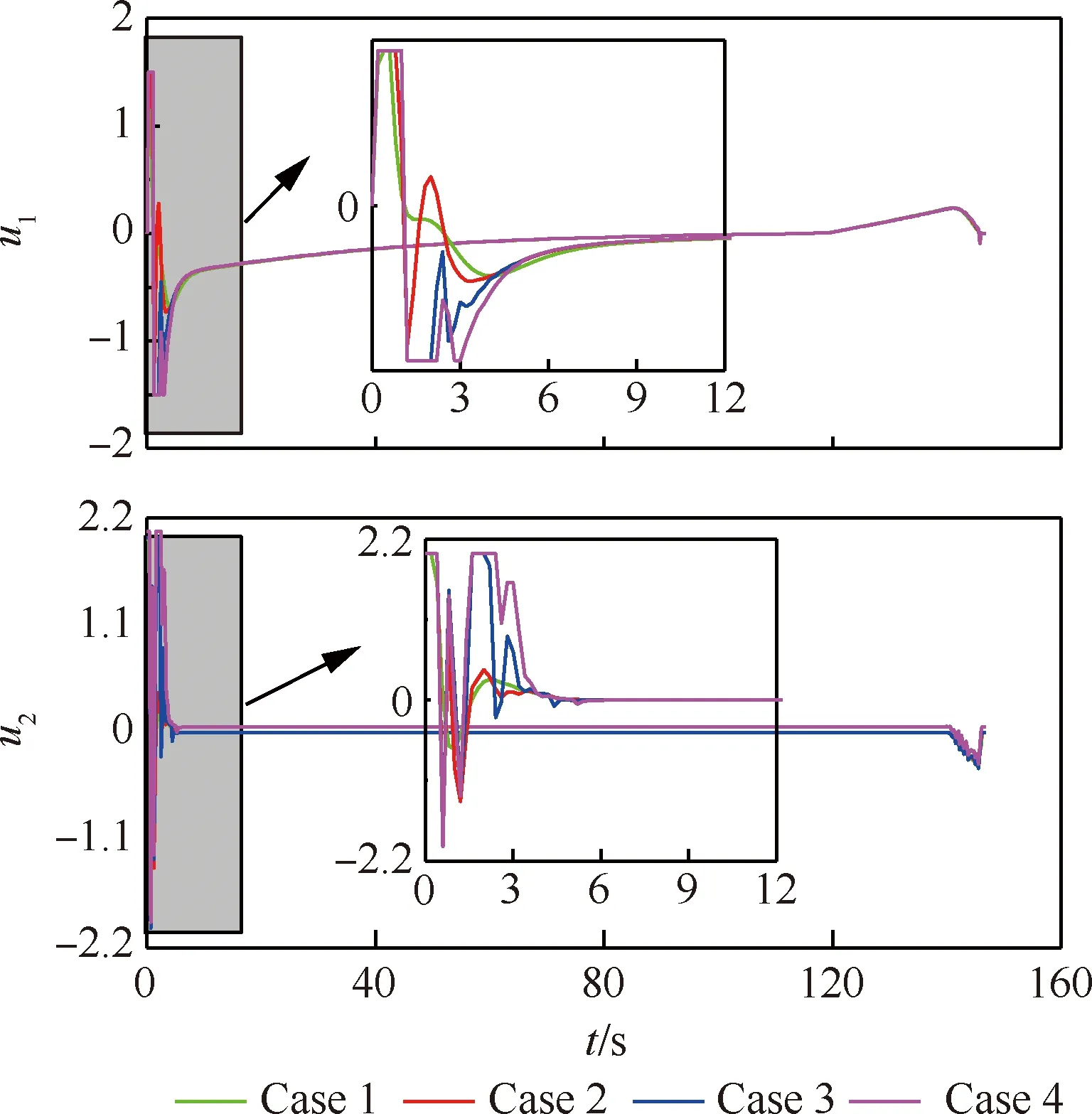
图6 不同权重系数情况下的单机滑行系统控制变量Fig.6 Control variables with different weight coefficientsfor single carrier-based aircraft system

为研究系统对不同初始偏差的敏感程度以及所提出的跟踪算法对初始偏差的抑制效果，本文选取4组不同的初始偏差组合进行仿真实验，权重系数P=diag(1×103,1×103,1.5×103,0)，具体初始偏差参数如表2所示。

根据上述初始偏差，采用本文所提出的算法，可得到横纵坐标以及角度的误差变化如图7所示。由图7可分析出：Case 5～8对应的误差变化均较为平稳，且均在10 s左右可以实现对初始偏差的有效抑制。此外，误差均满足式(37)，说明采用本文提出的在线算法可有效的抑制初始偏差，所得出的实际轨迹不会与障碍物发生任何碰撞。

为了进一步验证控制变量是否满足对应的约束关系，本文给出了对应的控制变量，具体如图8所示。

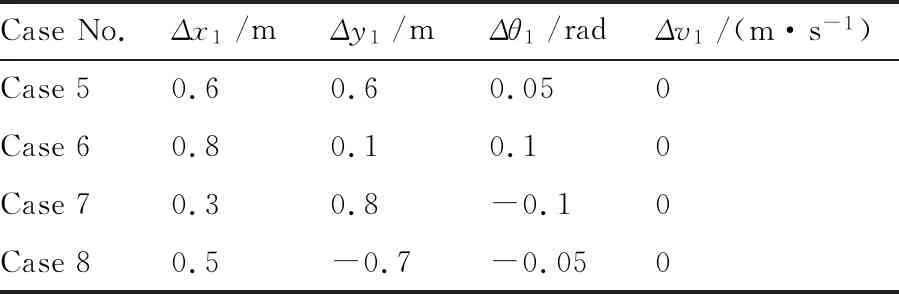
表2 单机滑行中不同初始偏差参数Table 2 Different initial deviations for singlecarrier-based aircraft system

图7 不同初始偏差情况下的单机滑行轨迹跟踪误差Fig.7 Tracking errors with different initial deviationsfor single carrier-based aircraft system

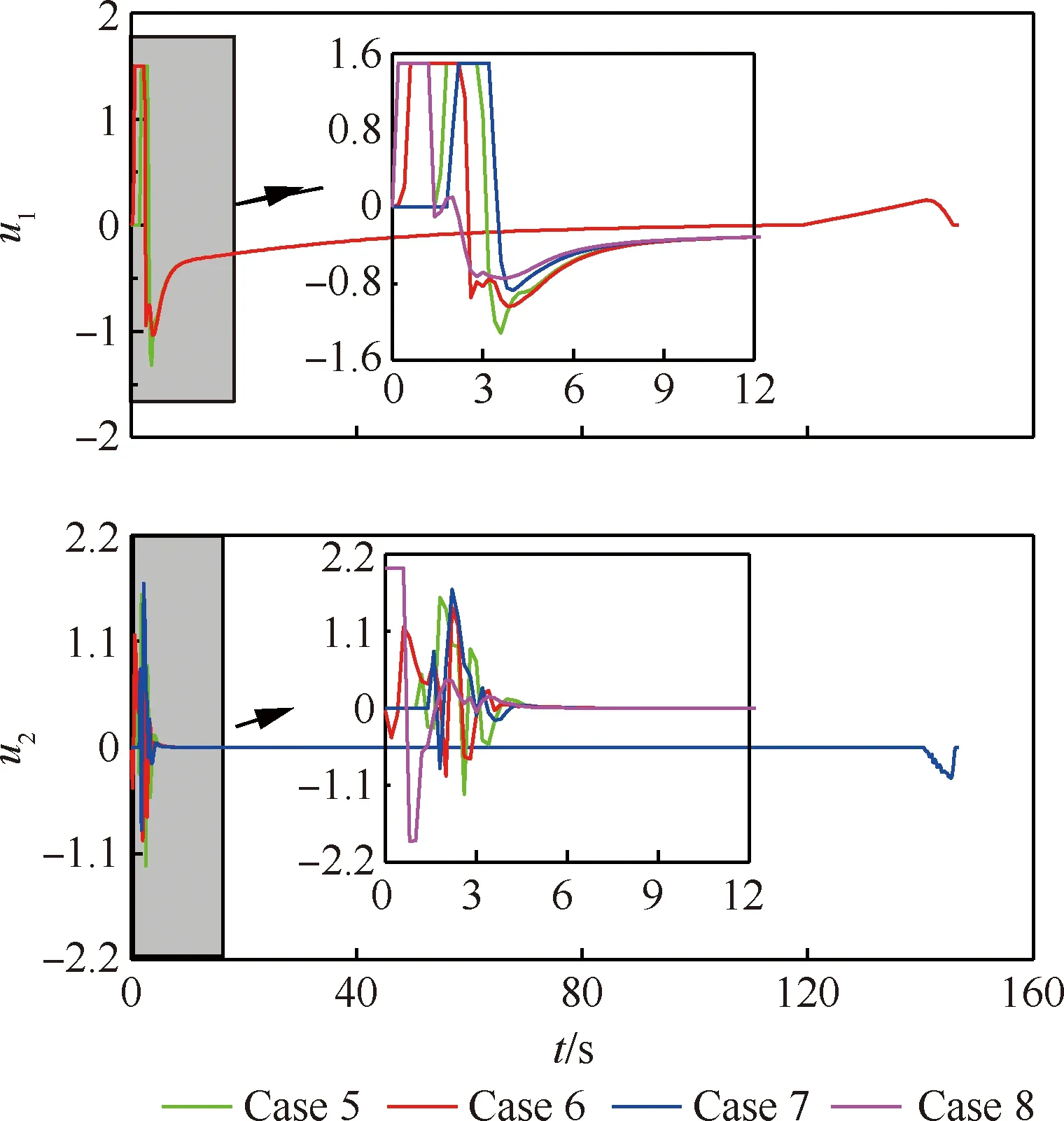
图8 不同初始偏差情况下的单机滑行系统控制变量Fig.8 Control variables with different initial deviationsfor single carrier-based aircraft system

由图8可分析出：在起始阶段，由于初始偏差的存在，需要不断的调节控制变量，以修正初始偏差，采用本文提出的算法可以在较短时间内完成这一过程；在有效抑制起始偏差后，对于不同的起始偏差，其对应的控制变量均呈现一致性的变化；所有的控制变量均在约束范围之内，即所得到的结果可完全满足相应的约束。

这说明，采用本文所提出的算法，可在较短时间内实现对初始偏差的修正，且所得到的结果可满足相应的状态变量以及控制变量约束关系。

4.2 持续外界扰动

在实际跟踪控制过程中，由于船体的晃动、测量误差等因素，会使实际轨迹偏离理想轨迹，为了研究本文提出的在线跟踪控制算法在持续外界扰动情况下的控制效果，本文将外界扰动考虑在内进行仿真实验。

此处将外界扰动设置为x1d=0.05cos(0.5t)，y1d=0.05sin(0.5t)，而θ1和v1的外界扰动均设置为0.005倍均值为0方差为1的正态分布随机噪声。将滚动窗口的步长设置为2 s，每个时间窗口内分为3大段，每一大段又分为3个小段，共计10个配点，滚动步长为0.2 s，在线跟踪算法的收敛精度为1×10-4。

此外，为了进一步验证本文算法的有效性，本文将所提出的算法与常用的BackwardSweep方法进行对比，具体结果如图9所示。由图9可分析出：采用本文所提出的在线跟踪算法可以实时的处理持续外界扰动，并将误差控制在较小的范围内；对于横坐标和纵坐标而言，采用本文提出方法对持续干扰的抑制效果明显优于BackwardSweep方法；对角度项而言，由于角度项的外界干扰幅值较小，两种方法没有明显的差别，但在末端附近，由本文提出方法所得到的角度误差明显小于BackwardSweep方法所得到的，且BackwardSweep方法所得到的角度误差幅值，在末端处有放大的趋势。

因此，较BackwardSweep方法而言，本文提出的在线跟踪方法，可将持续外界扰动引起的误差抑制在更小范围内，这说明了本文所提出的在线跟踪算法可更好的抑制外界扰动，在存在外界扰动的情况下，仍可以在线的调整控制策略以保证跟踪精度，这也充分说明所提出的跟踪算法具有良好的抗干扰能力。此外，在此次实验中，每次滚动计算平均需耗时7.43 ms，计算时间远低于BackwardSweep的46.12 ms，这也充分反映了本文所提出算法具有计算速度快的优点，完全可用于实时的在线跟踪问题。

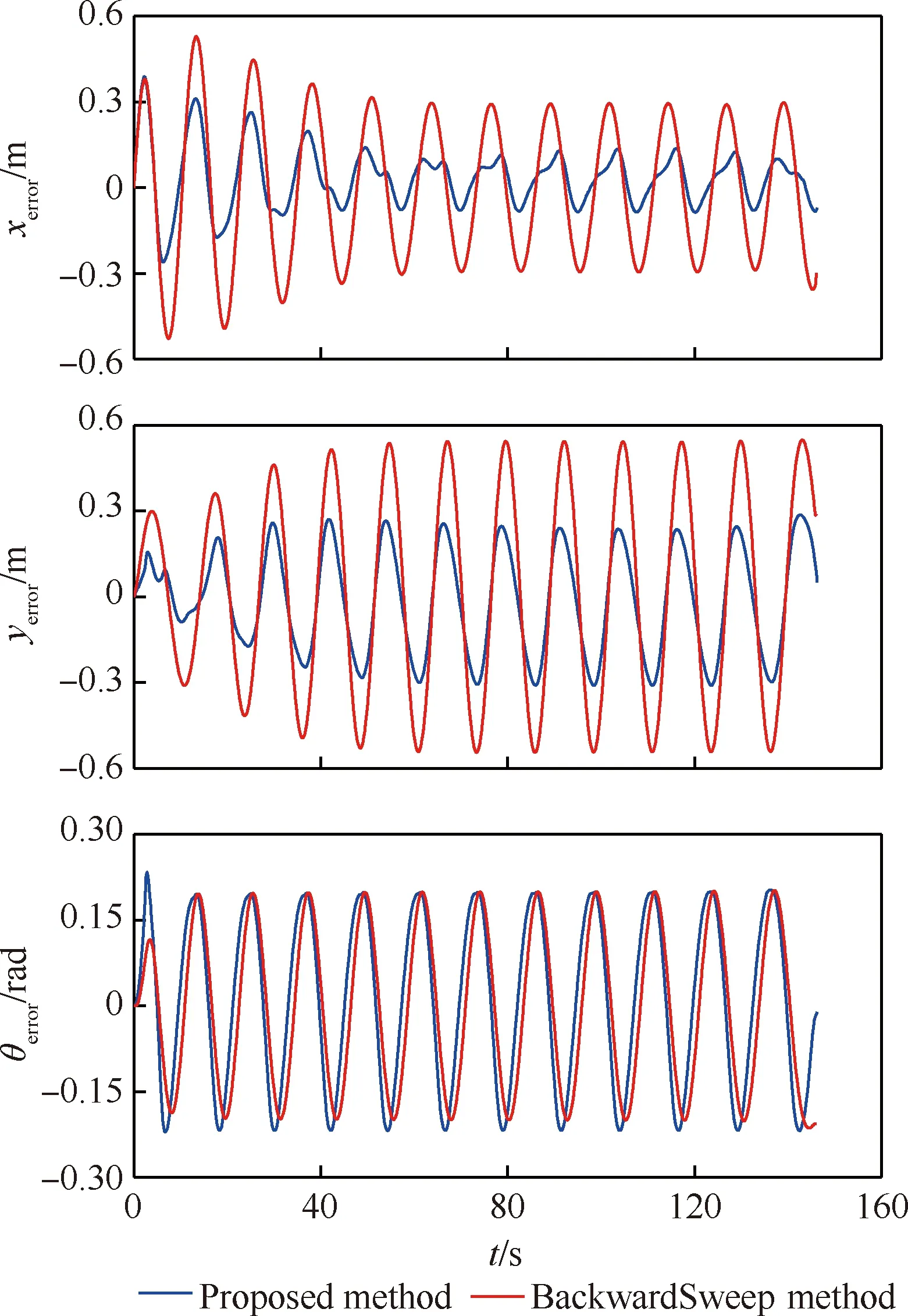
图9 持续外界扰动情况下的单机滑行轨迹跟踪误差Fig.9 Tracking errors with different continuous external disturbance for single carrier-based aircraft system

综上所述，本文所提出的基于滚动时域的在线跟踪最优控制算法，可以在存在持续外界扰动的情况下，实现对标准轨迹进行在线、实时的跟踪控制，较好的解决了非线性的跟踪控制问题，可有效的应用于舰载机滑行轨迹跟踪问题。

5 无杆牵引系统的轨迹跟踪控制

5.1 存在初始偏差

为了验证本文所提出的在线跟踪的在无杆牵引系统轨迹跟踪问题中的有效性，本文选取图4中红线所示的轨迹作为标准轨迹。根据所提出的连续非线性舰载机系统的轨迹跟踪模型，以及无杆牵引系统的运动学方程和相关的约束关系，采用本文所提出的在线跟踪最优控制算法，可实现对无杆牵引系统的轨迹进行跟踪。

根据无杆牵引系统的结构特点以及相关安全规定，其飞机的速度绝对值应该满足相应的约束，设|v1|≤1.2 m/s；牵引车的转向角也应满足其结构约束，设|u1|≤1.2；设牵引车的加速度绝对值应不大于2 m/s2，即|u2|≤2 m/s2；飞机与牵引车轴向夹角的绝对值不大于1 rad，即|θ2-θ1|≤1。与单机滑行轨迹跟踪类似，实际的轨迹还应满足式(37)的关系，本文取dist=1 m。

为研究不同的权重系数对无杆牵引系统跟踪效果的影响，以便选取合适的权重系数进行下一步研究，本文将R=diag(R1,R2)设置为单位矩阵，并采取不同的权重系数P=diag(P1,P2,P3,P4,P5)来进行仿真实验。而跟踪的主要目标是为了保证舰载机按照预定的轨迹运动，使舰载机可以被牵引至预定位置，所以主要的观测指标为舰载机的位置信息。此外，无杆牵引系统的初始偏差分别设为Δx1=0.2 m、Δy1=0.2 m、Δθ1=0.005、Δθ2=0、Δv2=0 m/s，P矩阵的取值如表3所示。

将滚动窗口的步长设置为2 s，每个时间窗口内分为3大段，每一大段又分为3个小段，共计10个配点，滚动步长为0.2 s，在线跟踪算法的收敛精度为1×10-4。分别采用不同的权重系数进行仿真实验，具体结果如图10所示。

表3 无杆牵引系统不同权重系数Table 3 Different weight coefficients for towed carrier-based aircraft system without drawbar

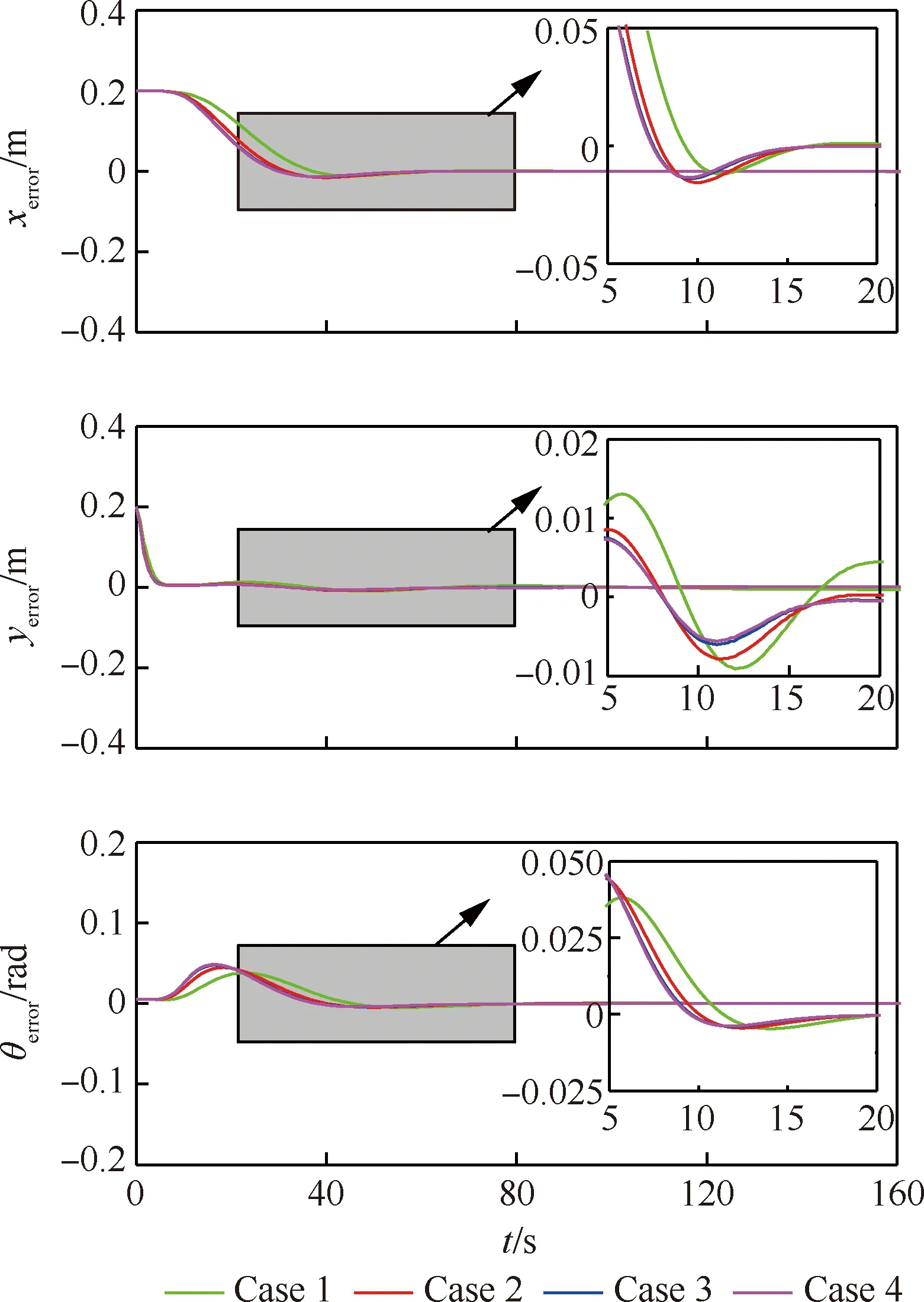
图10 不同权重系数情况下的无杆牵引系统轨迹跟踪误差Fig.10 Tracking errors with different weight coefficients for towed carrier-based aircraft system without drawbar

由图10可分析出：Case 1比对应的调节时间最长，其次为Case 2，Case 3和Case 4最短；对于Case 2～4，其调节时间和超调量均很接近。此外，在考虑误差的抑制情况时，还需考虑控制的平稳性，为了研究不同权重系数对控制平稳性的影响，本文给出了对应的控制变量，具体如图11所示。

由图11可分析出，Case 1对应的控制变量最平稳，其次为Case 2对应的控制变量，Case 4对应的控制变量变化相对较为剧烈。为了平衡误差的变化和控制变量的变化，本文将对应的权重系数设为103～104量级。

为研究系统对不同初始偏差的敏感程度以及所提出的跟踪算法对初始偏差的抑制效果，本文选取4组不同的初始偏差组合进行仿真实验，其中权重系数为P=diag(104,104,103,103,104)，具体初始偏差参数如表4所示。

根据上述初始偏差，采用本文所提出的算法，可得到横纵坐标以及角度的误差变化如图12所示。由图12可分析出：Case 5～8对应的误差变化均较为平稳，且均在30 s左右可以实现对初始偏差的有效抑制。此外，误差均满足式(37)，说明采用本文提出的在线算法可有效的抑制初始偏差，所得出的实际轨迹不会与障碍物发生任何碰撞。为了进一步验证控制变量是否满足对应的约束关系，本文给出了对应的控制变量，具体如图13所示。

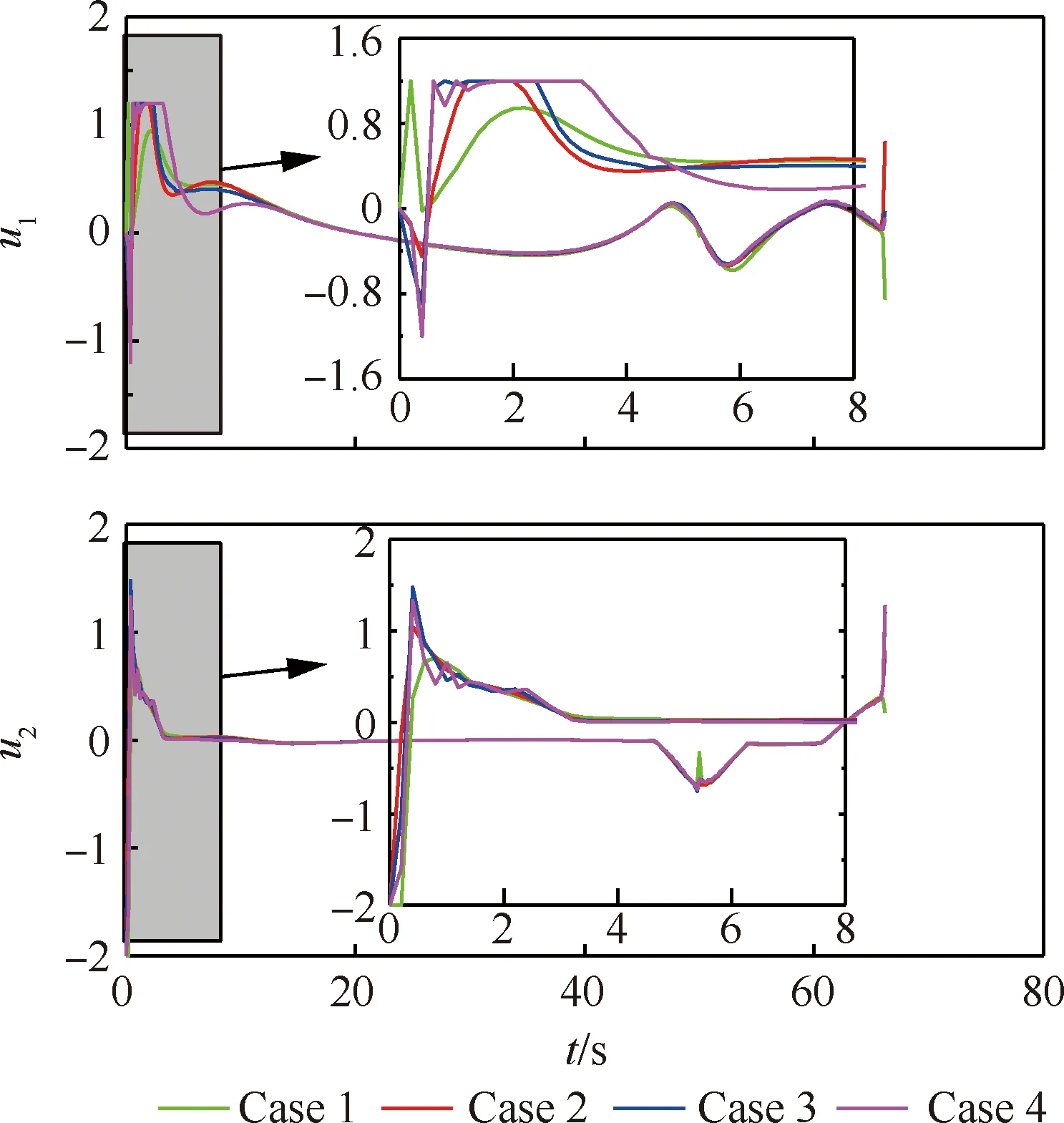
图11 不同权重系数情况下的无杆牵引系统控制变量Fig.11 Control variables with different weight coefficients for towed carrier-based aircraft system without drawbar

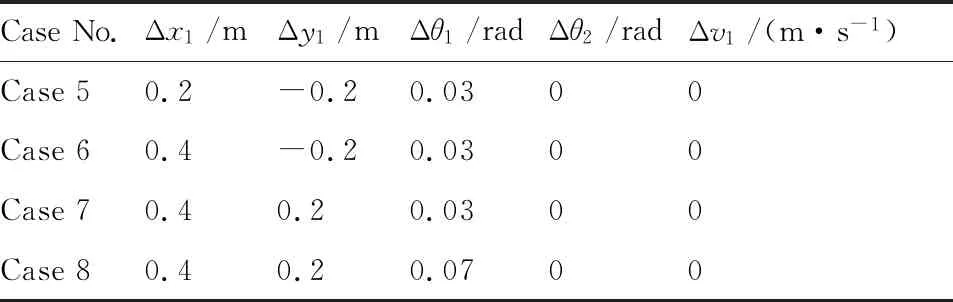
表4 无杆牵引系统不同初始偏差参数Table 4 Different initial deviations for towed carrier-based aircraft system without drawbar

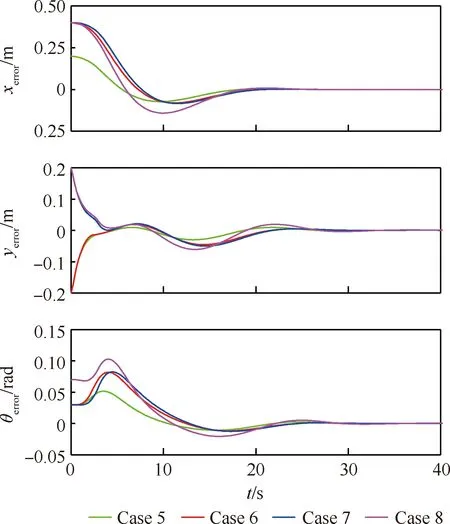
图12 不同初始偏差情况下的无杆牵引系统误差Fig.12 Tracking errors with different initial deviations for towed carrier-based aircraft system without drawbar

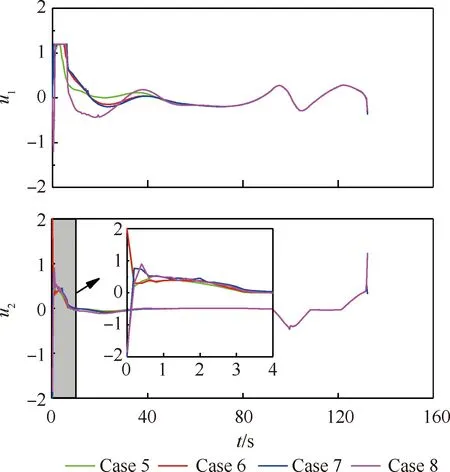
图13 不同初始偏差情况下的无杆牵引系统控制变量Fig.13 Control variables with different initial deviations for towed carrier-based aircraft system without drawbar

由图13可分析出：在起始阶段，由于初始偏差的存在，需要不断的调节控制变量，以修正初始偏差，采用本文提出的算法可以在较短时间内完成这一过程；所有的控制变量均在约束范围之内，即所得到的结果均可完全满足相应的约束。

为了进一步验证由本文提出的在线跟踪算法可满足无杆牵引系统跟踪的相关约束关系，本文给出了舰载机与无杆牵引车轴向之间的夹角β1以及舰载机的实际速度v1随时间的变化关系，具体如图14所示。

图14 不同初始偏差情况下无杆牵引系统中β1和v1变化关系Fig.14 Variation between β1 and v1 with different initial deviations for towed carrier-based aircraft system without drawbar

由图14可分析出：舰载机与无杆牵引车轴向之间的夹角以及舰载机的实际速度变化均非常平缓，且舰载机与无杆牵引车纵向之间夹角的绝对值均未超过1，完全满足|β1|≤1的约束关系；舰载机实际速度的绝对值也未超过1.2 m/s，即完全满足|v1|≤1.2 m/s的约束关系。

这说明，采用本文所提出的算法，可在较短时间内实现对初始偏差的修正，且所得到的结果可满足相应的状态变量以及控制变量约束关系。

5.2 持续外界扰动

为了研究本文提出的在线跟踪控制算法在持续外界扰动情况下的控制效果，此处将外界扰动考虑在内进行仿真实验。设外界扰动为x1d= 0.01cos(0.5t)，y1d=0.01sin(0.5t)，θ1d=0.001 sin(0.5t)，而θ2和v2的外界扰动均设置为0。将滚动窗口的步长设置为2 s，每个时间窗口内分为3大段，每一大段又分为3个小段，共计10个配点，滚动步长为0.2 s，在线跟踪算法的收敛精度为1×10-4。

此外，为了进一步验证本文算法的有效性，将所提出的算法与常用的BackwardSweep方法进行对比，具体结果如图15所示。

由图15可分析出：采用本文所提出的在线跟踪算法可以实时的处理持续外界扰动，并将误差控制在较小的范围内。在50 s之前，对于舰载机横坐标和角度而言，采用本文提出算法对持续干扰的抑制效果明显优于BackwardSweep方法；对于纵坐标误差的抑制效果而言，两种方法没有明显的差别。但在50 s之后，所得到的舰载机横、纵坐标以及角度误差均有放大的趋势。这主要是因为在50 s之后，无杆牵引车由拖着舰载机正向行驶变为倒推着舰载机进入停机位，该过程系统的速度由正向变为负向，速度的符号发生了改变，系统的控制更加不稳定，对误差更加敏感。即使如此，由本文提出算法所得到的舰载机横、纵坐标以及角度误差仍明显小于 BackwardSweep 方法所得到的。

此外，在此次实验中，每次滚动计算平均需耗时9.12 ms，计算时间远低于BackwardSweep的57.31 ms，这也充分反映了本文所提出算法具有计算速度快的优点，完全可用于实时的在线跟踪问题。

综上所述，本文所提出的基于滚动时域的在线跟踪最优控制算法，可有效应用于无杆牵引系统的轨迹跟踪问题。

6 有杆牵引系统的轨迹跟踪控制

6.1 存在初始偏差

为了验证本文所提出的在线跟踪的在有杆牵引系统轨迹跟踪问题中的有效性，本文选取图4中蓝线所示的轨迹作为标准轨迹。根据有杆牵引系统的结构特点以及相关安全规定，其飞机的速度绝对值应该满足相应的约束，设|u2|≤1.2 m/s；牵引车的转向角也应满足其结构约束，设|u1|≤1.5(牵引车转向角的绝对值不大于0.982 8)；飞机与牵引车轴向夹角的绝对值不大于1 rad，即|β1|≤1；牵引车与牵引杆轴向夹角的绝对值不大于1 rad，即|β2|≤1。与单机滑行轨迹跟踪类似，实际的轨迹还应满足式(37)的关系，本文取dist=1 m。

为研究不同的权重系数对有杆牵引系统跟踪效果的影响，以便选取合适的权重系数进行下一步研究，本文将R=diag(R1，R2)设置为单位矩阵，并采取不同的权重系数P=diag(P1，P2，P3，P4，P5)来进行仿真实验。此外，有杆牵引系统的初始偏差分别设为Δx1=0.4 m、Δy1=0.4 m、Δθ1=0.1、Δβ1=0.001、Δβ2=0.001，P矩阵的取值可见表5。

表5 有杆牵引系统不同权重系数Table 5 Different weight coefficients for towed carrier-basedaircraft system with drawbar

将滚动窗口的步长设置为2 s，每个时间窗口内分为3大段，每一大段又分为3个小段，共计10个配点，滚动步长为0.2 s，在线跟踪算法的收敛精度为1×10-4。分别采用不同的权重系数进行仿真实验，具体结果如图16所示。

由图16可分析出，Case 1比对应的调节时间最长，其次为Case 2，Case 3和Case 4最短；对于Case 3～4，其调节时间和超调量均很接近。在终端误差方面，Case 1～4对应的终端误差均可保持在很小的范围内，其中Case 3和Case 4对应的终端误差比较接近，且较Case 1和Case 2均更小。在57～75 s这个阶段，所得到的舰载机横、纵坐标以及角度误差均有放大的趋势，这主要是因为在这段时间内，牵引车由拖着舰载机正向行驶变为倒推着舰载机进入停机位，该过程系统的速度由正向变为负向，速度的符号发生了切换，系统的控制更加不稳定，对误差更加敏感。

此外，在考虑误差的抑制情况时，还需考虑控制的平稳性，为了研究不同权重系数对控制平稳性的影响，本文给出了对应的牵引车控制变量，具体如图17所示。由图17可分析出，Case 1对应的控制变量最平稳，其次为Case 2对应的控制变量，Case 4对应的控制变量变化相对较为剧烈。为了平衡误差的变化和控制变量的变化，本文将舰载机位置项对应的权重系数设置为103～104量级。

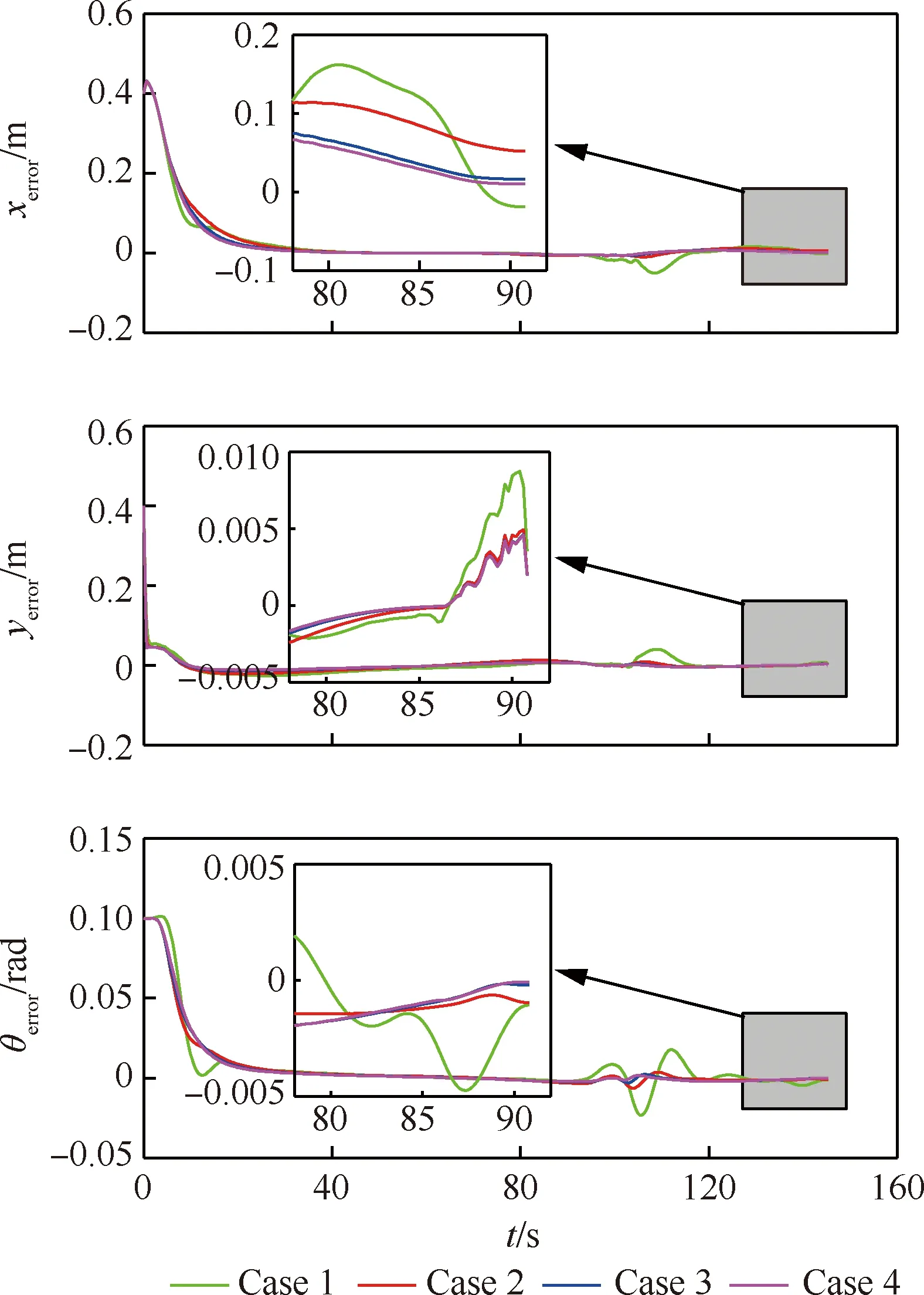
图16 不同权重系数情况下的有杆牵引系统轨迹跟踪误差Fig.16 Tracking errors with different weight coefficients for towed carrier-based aircraft system with drawbar

为研究系统对不同初始偏差的敏感程度以及所提出的跟踪算法对初始偏差的抑制效果，本文选取4组不同的初始偏差组合进行仿真实验，其中权重系数为P=103×diag(10，10，5，0，0)，具体初始偏差参数如表6所示。

根据上述初始偏差，采用本文所提出的算法，可得到横纵坐标以及角度的误差变化如图18所示。由图18可分析出：Case 5～8对应的误差变化均较为平稳，且均在25 s左右可以实现对初始偏差的有效抑制。此外，误差均满足式(37)，说明采用本文提出的在线算法可有效的抑制初始偏差，所得出的实际轨迹不会与障碍物发生任何碰撞。为了进一步验证控制变量是否满足对应的约束关系，本文给出了牵引车的速度和转向角，具体如图19所示。

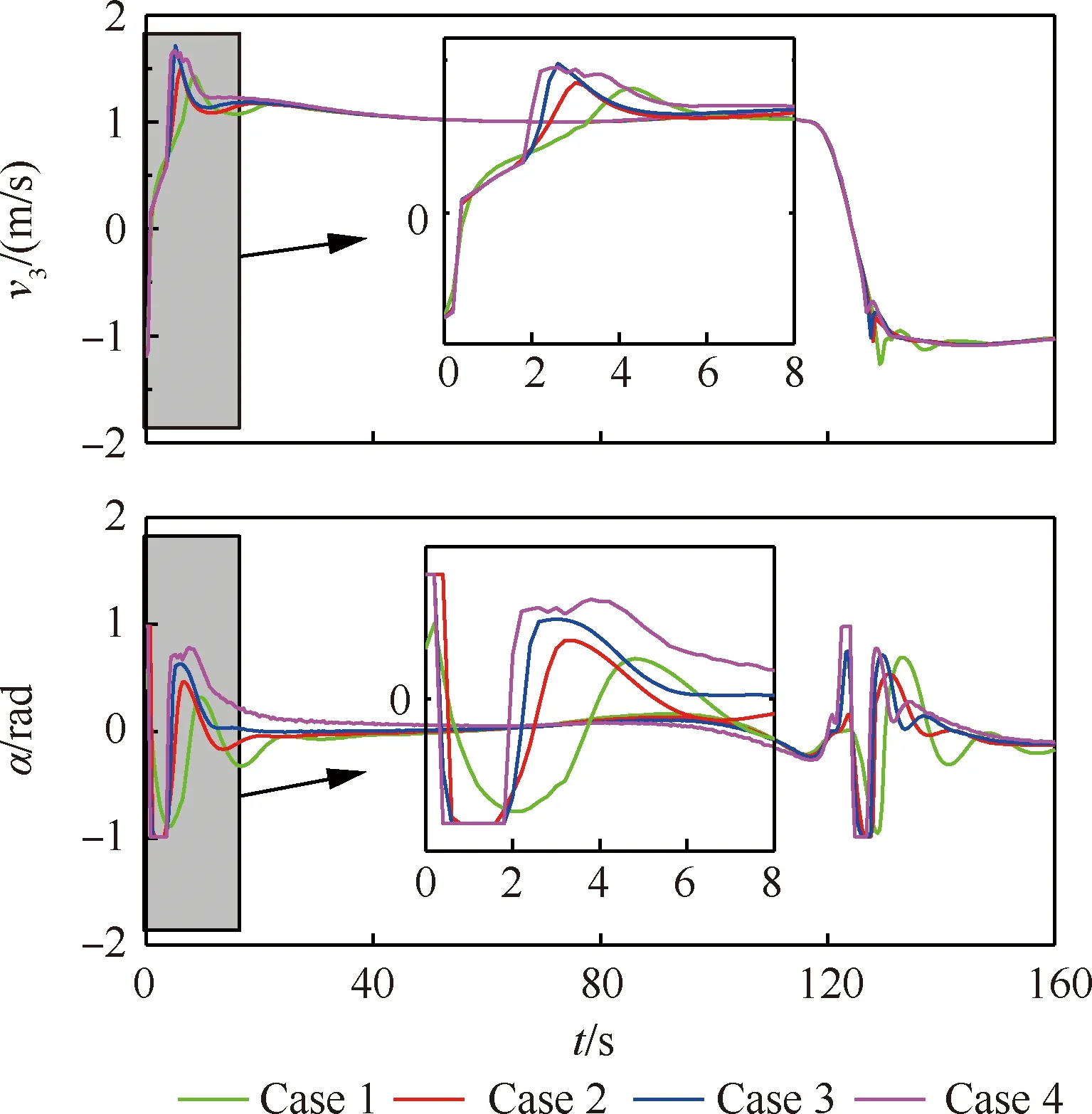
图17 不同权重系数情况下的有杆牵引系统控制变量Fig.17 Control variables of tractor with different weight coefficients for towed carrier-based aircraft system with drawbar

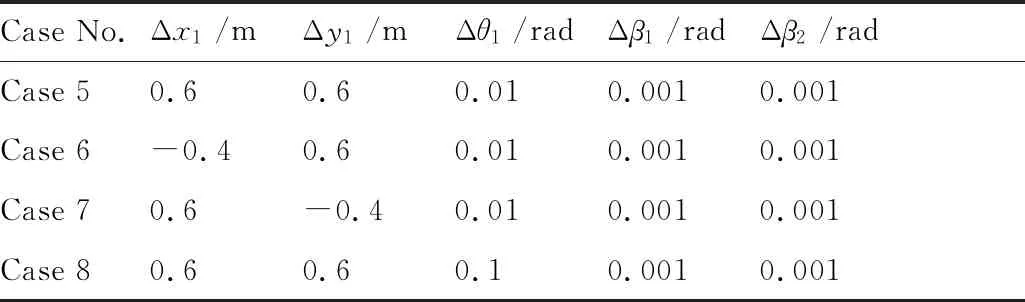
表6 有杆牵引系统不同初始偏差参数Table 6 Different initial deviations for towed carrier-basedaircraft system with drawbar

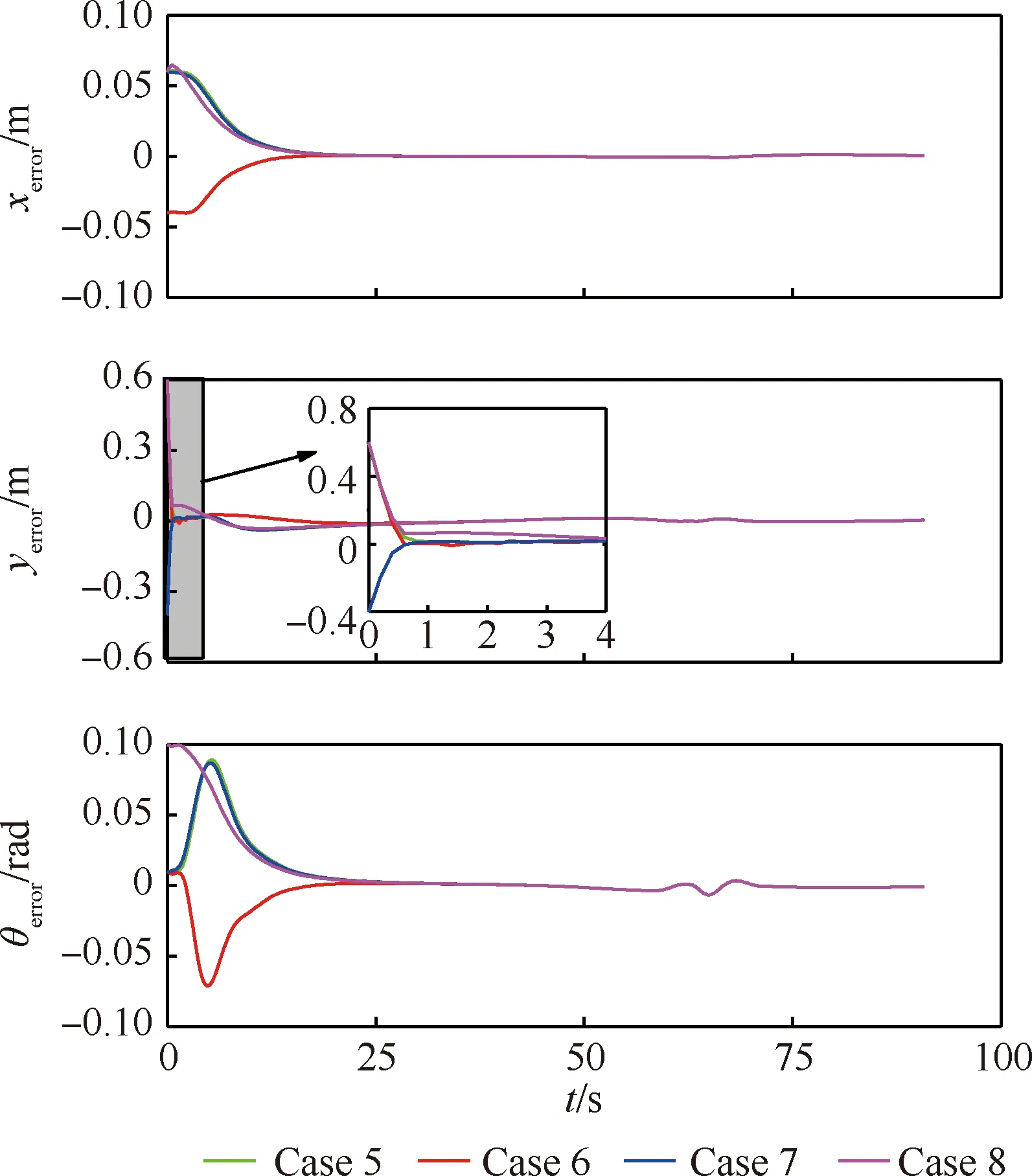
图18 不同初始偏差情况下的有杆牵引系统轨迹跟踪误差变化图Fig.18 Tracking errors with different initial deviations for towed carrier-based aircraft system with drawbar

由图19可分析出：在起始阶段，由于初始偏差的存在，需要不断的调节牵引车速度和转向角以修正初始偏差，采用本文提出的算法可以在较短时间内完成这一过程；牵引车的转向角均未超过0.982 8，即对应的控制变量在约束范围之内。且在终端位置时，牵引车的速度可保持在0 m/s，根据公式舰载机与牵引车之间的速度关系可知，舰载机的速度在末端也为0 m/s。

为了进一步验证由本文提出的在线跟踪算法可满足有杆牵引系统跟踪的相关约束关系，本文给出了β1以及β2随时间的变化关系，具体如图20所示。

由图20可分析出：舰载机与牵引杆轴向之间的夹角以及牵引车与牵引杆轴向之间的夹角变化均非常平缓，且二者的绝对值均未超1，完全满足|β1|≤1和|β2|≤1的约束关系。

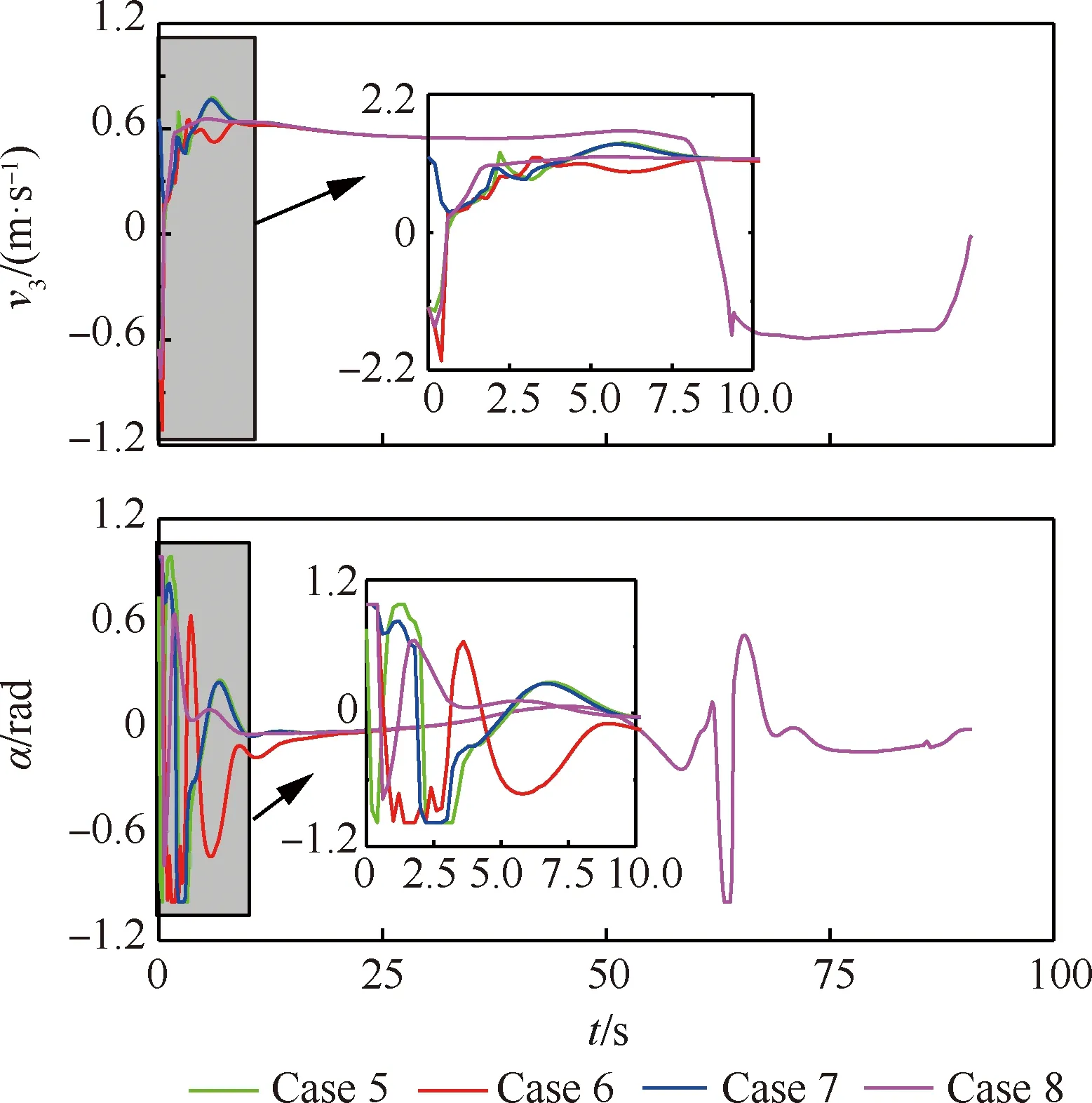
图19 不同初始偏差情况下的有杆牵引系统速度和转向角Fig.19 Velocity and steering angle of tractor under different initial deviations for towed carrier-based aircraft system with drawbar

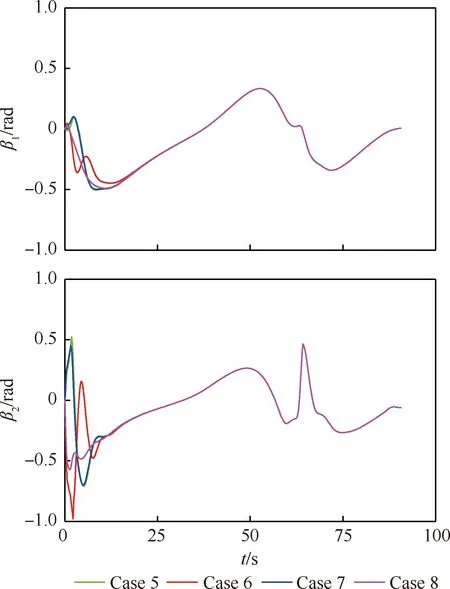
图20 不同初始偏差情况下的β1和β2变化关系Fig.20 Variation ofβ1 and β2 with different initial deviations

这说明，采用本文所提出的算法，可在较短时间内实现对初始偏差的修正，且所得到的结果可满足相应的状态变量以及控制变量约束关系。

6.2 持续外界扰动

为了研究在持续外界扰动情况下的控制效果，此处将外界扰动设置为x1d=0.02cos(0.5t)，y1d=0.02sin(0.5t)，θ1d=0.002cos(0.5t)，β1d=0.002cos(0.5t)，β2d=0.002cos(0.5t)。将滚动窗口的步长设置为2 s，每个时间窗口内分为3大段，每一大段又分为3个小段，共计10个配点，滚动步长为0.2 s，在线跟踪算法的收敛精度为1×10-4。具体结果如图21所示。

由图21可分析出：采用本文所提出的在线跟踪算法可以实时的处理持续外界扰动，并将误差控制在较小的范围内。且可将终端误差控制在较小的范围内，并可以较高的精度将舰载机牵引至预定位置。

此外，在此次实验中，每次滚动计算平均需耗时11.12 ms，计算时间远低于BackwardSweep的71.86 ms，这也充分反映了本文所提出算法具有计算速度快的优点，完全可用于实时的在线跟踪问题。

综上所述，本文所提出的基于滚动时域的在线跟踪最优控制算法，可有效应用于有杆牵引系统的轨迹跟踪问题。

图21 持续外界扰动情况下的有杆牵引系统轨迹跟踪误差Fig.21 Variation of tracking errors with different continuous external disturbance for towed carrier-based aircraft system with drawbar

7 3种方式的轨迹跟踪控制特性对比分析

在前文中已经证明了本文所提出的算法可很好的应用于单机滑行、无杆牵引系统以及有杆牵引系统的轨迹跟踪问题，但由于这3种方式所对应的系统结构以及运动学方程差别较大，因此有必要根据各自的跟踪结果来研究这3种方式的跟踪控制特性。

7.1 初始偏差对3种系统轨迹跟踪的影响

为了研究单机滑行、无杆牵引系统以及有杆牵引系统的控制特性，本文首先从不同初始偏差对控制结果的影响角度来进行分析。由于这3种系统运动学方程的状态变量中均存在舰载机横坐标、纵坐标以及角度这3项，在比较不同初始偏差对3种系统控制结果的影响时，可只考虑这3项的初始偏差。

表7中给出了不同的舰载机横坐标、纵坐标以及角度初始偏差，单机滑行、无杆牵引系统以及有杆牵引系统中其它状态变量的初始偏差均记为0。由于这3种系统的运动学方程和约束不一样，权重对不同系统的影响也会有差别，为了对比初始偏差对3种系统的影响，此处可根据不同系统的特点来设置可以使跟踪控制效果达到最优的权重系数。其中，跟踪控制效果主要从以下3个角度来衡量：

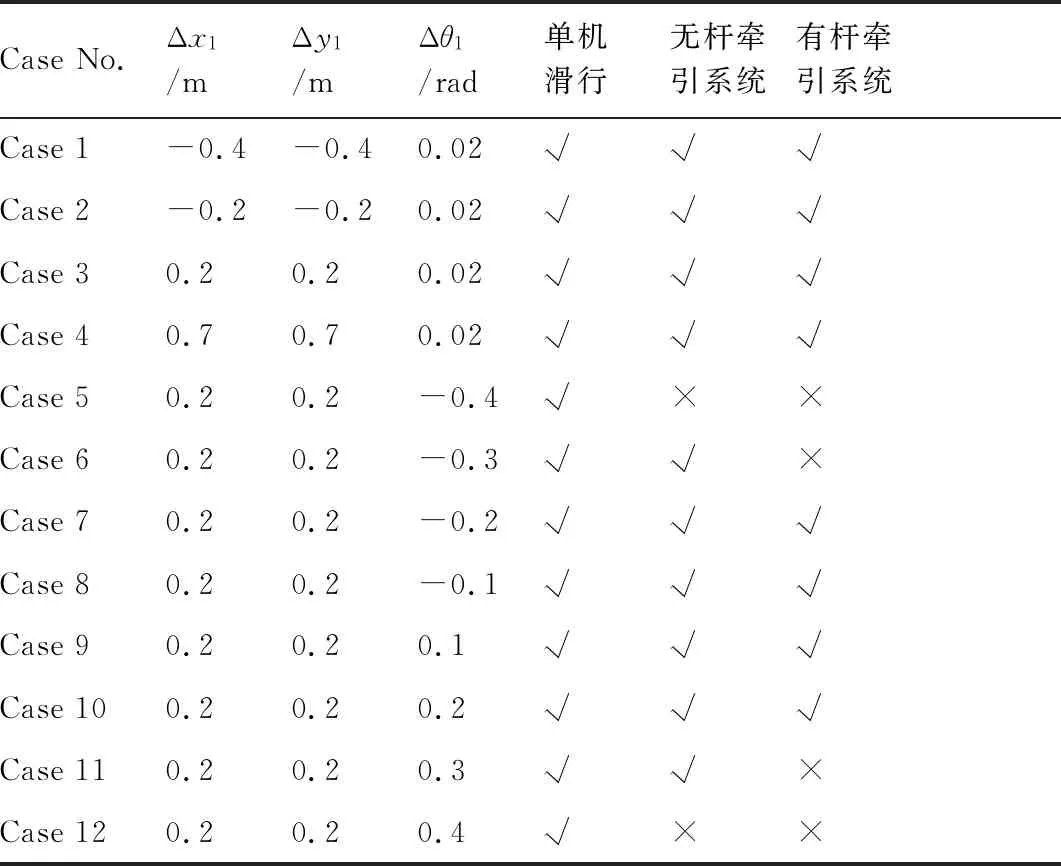
表7 不同初始偏差条件下的跟踪结果Table 7 Tracking results with different initial deviations

1)所得到的控制变量需满足对应的约束关系。

2)所得到的状态变量需满足对应的约束关系。

3)末端误差的绝对值需不大于0.05。

若以上3个衡量指标均成立，则说明可有效抑制所设置的初始偏差；否则，则视为不可抑制该初始偏差。

本文采取12组不同的初始偏差分别对3种系统进行跟踪实验，具体结果如表7所示。Case 1～4是采用固定的舰载机角度初始偏差，选取不同幅度的位置初始偏差来进行仿真实验。由Case 1～4的实验结果可分析出：单机滑行、无杆牵引系统以及有杆牵引系统均可对不同幅度的位置偏差进行有效抑制。

Case 5～12是采用固定幅度的位置初始偏差，选取不同幅度的角度偏差来进行仿真实验。由Case 5～12的实验结果可分析出：单机滑行系统可有效抑制不同幅度的角度初始偏差，即对角度偏差敏感度低；无杆牵引系统可有效抑制一定幅度范围内的角度初始偏差，对角度偏差的敏感度较单机滑行系统高；有杆牵引系统能有效抑制角度初始偏差的范围最小，对角度偏差的敏感度最高。

综合分析上述结果可得出：单机滑行、无杆牵引系统以及有杆牵引系统在舰载机初始角度偏差较小的情况下，均可抑制较大幅度的位置初始偏差，但有杆牵引系统对舰载机角度初始偏差最为敏感，在使用有杆牵引车调运舰载机的过程中，应在调运之前尽可能的将舰载机调整至预定角度；相对于有杆牵引系统而言，无杆牵引系统对舰载机角度初始偏差的敏感度要低，但若角度的初始偏差太大，也无法实现有效跟踪；而舰载机滑行系统对初始偏差的敏感度最低。

7.2 外界扰动对3种系统轨迹跟踪的影响

为了研究单机滑行、无杆牵引系统以及有杆牵引系统的控制特性，同时使仿真结果更加贴近实际情况，本文还从不同幅度的持续外界干扰对跟踪控制结果的影响角度来进行分析。由于这3种系统运动学方程的状态变量中均存在舰载机横坐标、纵坐标以及角度这三项，在比较不同幅幅度外界干扰对3种系统控制结果的影响时，只考虑这三项的初始偏差。设舰载机横坐标受到的外界干扰为x1d=Δrcos(0.5t)，纵坐标受到的外界干扰为y1d=Δrsin(0.5t)，舰载机角度受到的外界干扰为θ1d=0.1Δrcos(0.5t)，其中Δr为外界干扰幅度参数。

此处可根据不同系统的特点来设置可以使跟踪控制效果达到最优的权重系数。其中，跟踪控制效果主要从以下3个角度来衡量：

1)所得到的控制变量需满足对应的约束关系。

2)所得到的状态变量需满足对应的约束关系。

若以上3个衡量指标均成立，则说明该系统可有效抑制所设置的持续外界干扰；否则，则视为不可抑制。

则采用本文提出的跟踪算法，可得到不同幅度持续外界扰动条件下的跟踪结果。本文在10组不同幅度的持续扰动信号情况下，分别对3种系统进行跟踪实验，具体结果如表8所示。

由表8可分析出：在该仿真实验中，舰载机角度项的持续扰动幅度较小，单机滑行系统可对较大幅度的持续干扰进行有效抑制，有杆牵引系统可抑制的持续干扰幅度范围较单机滑行系统小，而无杆牵引系统可抑制的持续干扰幅度范围最小。

结合初始偏差的对比结果可得出如下结论：

表8 不同幅度持续外界扰动条件下的跟踪结果统计表Table 8 Tracking results with continuous external disturbance of different amplitude

1)当舰载机角度项的偏差较小时，单机滑行系统对舰载机横、纵坐标偏差的抑制能力最强，其次为有杆牵引系统，最后为无杆牵引系统；故在此情况下，单机滑行对海况的要求最低，其次为采用有杆牵引的方式，而采用无杆牵引的方式对海况要求最高。

2)从对舰载机角度偏差的敏感程度而言，有杆牵引系统最敏感，无杆牵引系统次之，单机滑行系统对舰载机角度偏差的敏感程度最低。

8 结 论

本文针对单机滑行、无杆牵引系统以及有杆牵引系统的轨迹跟踪问题进行了研究，首先将这3种系统的轨迹跟踪问题转化为最优控制问题，并建立了连续非线性舰载机系统的轨迹跟踪模型；然后基于第三类生成函数，提出了适用范围更广的全状态保辛伪谱算法，并结合滚动时域理论提出了基于滚动时域的在线跟踪最优控制方法，证明了所提出的算法是一种保辛算法。最后，通过具体的仿真实验验证了本文提出算法的有效性，并对3种不同方式的跟踪特性进行了对比分析。本文所提出的算法具有以下优点：

1)可以求解有限时间区间的最优跟踪控制问题，避免求解复杂的Riccati方程(ARE)，而传统跟踪控制算法难以避免。

2)舰载机系统的真实轨迹不能与障碍物发生碰撞，因此控制变量和状态变量应该满足相应的约束关系，传统的跟踪方法难以同时解决控制约束和状态约束的跟踪问题，而所提出的算法能较好地解决这一问题，且跟踪精度较高。

3)降低了传统非线性最优控制算法对初始参考解和协变量的敏感程度。

4)计算效率高，可以达到实时跟踪的目的，一定程度上解决了最优控制算法不适用于在线跟踪的问题，且在有扰动的情况下仍可进行高精度的、实时的跟踪控制，鲁棒性强。

为了提高算法效率，在今后的工作中需要对其进一步优化。此外，如何平衡计算效率、精度之间的关系是另一项具有挑战性的工作。