关注细节，成就小学数学高效课堂

冯群芳

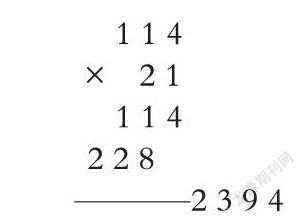
在真实的课堂里，学生充分自主，神情投入；教师悉心倾听，真情奔涌。师生宽松和谐、互动合作、情趣横生的空间里展开心灵的对话，在对话中引导，在引导中感悟。因此，教师的教学设计应更多地思考学生如何“学”，突出学生自己钻研、领悟和感受的过程。那么，如何在教学中提高课堂效果呢？下面，笔者摘取了一些教学片断，谈谈一些分析和反思。

一、自主探索，实践交流

2.分析

以上教学中，笔者给学生提供大量的动手操作时间，折一折、画一画、想一想和说一说的环节中抓住教学细节，鼓励学生独立思考，从不同的角度去探究问题，让学生借助操作自我理解分数乘分数的计算方法，让学生在探索交流中发展能力，动手操作中提升思维，从而达到了计算技能与思维发展的双赢，提高课堂的效果。

二、情理合一，算法多样

1.探索三位数乘两位数的计算方法

师：114×21到底等于多少呢？你准备怎样算？谁来谈谈？

生1：我打算把21套书拆成两部分来计算。

生2：我打算用竖式来试试。

……

师：光有想法不行，我们还要行动起来。

（学生在练习本展开探究，教师巡视指导，发现案例。）

师：你是怎样算的？谁先来展示一下？

生1：我先把21分成20和1，先算114×20=2280（元），再算114×1=114（元），最后算2280+114=2394（元）

师：对于他的算法，你有疑问吗？

生2：你为什么要把21分成20和1来算？

生1：我把21套分成20套和1套來算，先算出20套的价钱：114×20=2280（元），再算1套的价钱：114×1=114（元），最后算出21套的总价：2280+114=2394（元）

生2：你的方法真好，向你学习！

师：还有不同的算法吗？

生3：我也是把21分开来算的，不过我把21拆成3×7，然后用114×3×7=2394（元）

师：谁有不懂的地方吗？

生4：你为什么要这样拆呢？

生3：因为114×3=342（元）是表示先算出3套的价钱，21套里有7个这样的3套，所以再算342×7=2394（元）

生4：哦，我明白了，谢谢你！

师：一问一答中，我们又读懂了一种方法，谢谢你们！谁还想来说说？

生5：我是用竖式计算的，先算1×114=114，再算20×114=2280，最后将两次乘得的积加起来：114+2280=2394，你们看：

1 1 4

× 2 1

1 1 4

2 2 8

2 3 9 4

师：有哪个同学不明白吗？

生6：请问“228”表示什么意思？为什么228后面没有数的呢？

生5：“228”是表示228个十，因为是用十位上的2去乘114，等于228个十。

生6：哦，“228”是表示228个十，我明白了，谢谢你！

师：我也有疑问，用十位上的“2”乘114时，所得的积从哪位写起？

生5：从十位写起，因为2个十乘114等于228个十，所以228后面就可以省略一个“0”了。

师：谢谢你的提醒！

师：同学们，用自己的方法来解决问题，是件了不起的事；能听懂或看懂别人的想法，也是一件了不起的事！你看，老师也带来了一种方法，谁读懂了？

2000+200+80+100+10+4=2394

生7：这种方法是将114分成100+10+4；再将21分拆成20和1，先将20分别与100、10和4相乘，再将1分别与100、10和4相乘，最后将6次乘得的积加起来。

生8：我觉得这种方法太麻烦了！

生9：我也觉得也乘6次，还要把6次乘得的积加起来，太繁琐了！

……

师：同学们，这些都是我们想到的或者读懂的方法。仔细观察这些方法，你有什么发现？

生1：我发现了它们的结果是相同的。

生2：虽然它们的结果相同，但方法不同。

生3：我发现了它们虽然方法不同，但是有联系的，它们都是在拆数。你看，第一种方法是把21拆成20和1，然后分别与114相乘；第二种方法是把21拆成3×7；而竖式是先算1×114=114，再算20×114=2280，其实也是把21拆成20和1，然后分别与114相乘。

师：思维敏捷，表达清晰，让人一听就懂，此处该有掌声！那这些方法中，你喜欢哪种方法？

生6：我喜欢竖式，因为它能算得又对又快。

生7：我也喜欢竖式，它很简便。

……

师：不管你用的是哪种方法，最后的结果都是2394。平时计算中，我们没有必要把每种方法都用上，只要选择合适的，有把握算准就可以了。

2.分析

算法多样化是新课程改革所倡导的新理念之一，它为沉寂的计算教学带来了新的方法，注入了新的活力。上述教学，教师在细节中不仅尊重学生的独立思考，还鼓励学生探索不同的方法，体现了以学生为主的教学原则。通过多种算法的呈现给学生提供了学习、思考、交流、分享的平台。有了算法的多样化，才有讨论交流的必要，从而形成生生互动，师生互动的高效课堂。

三、制造冲突，激发欲望

1.探索平行四边形角的特点

师：通过测量平行四边形四个角的度数，你有什么发现？

生：有两个锐角相等，有两个钝角也相等。

师：两个相等的角处在什么位置？

生：一个上，一个下。

师：是不是相对的？其实像这样的角叫对顶角。这个平行四边形的对顶角相等，其它平行四边形呢？

（学生赶紧从书上找平行四边形验证）

生1：我量了两个平行四边形，它们的对顶角都相等。

生2：我量的也是。

生3：平行四边形的对顶角都相等。

师：如果要你量平行四边形角的度数，你量几次？

（这时，教室里的学生“吵”了起来：有的认为要量两次，有的认为要量一次）

师：请你们说出各自的想法好吗？

生1：我认为只要量一次，因为我们昨天就知道四边形的内角和是360度，用360减去量出的两个角的度数，再除以2就是另外一个角的度数。

生2：太麻烦了，平行四边形有两个相等的锐角，两个相等的钝角，用360除以2就是一个锐角和一个钝角的和，是180度。

生3：平行四边形的一个锐角加一个钝角就是180度。直接用180减量出角的度数就知道每个角的度数了。

（随后，我随意出示了几个平行四邊形，学生根据这一点，一下子就计算出了每个角的度数）

师：现在给你一个平行四边形，你认为要量几次？

生：一次。

2.分析

在教学问题的设计安排上，笔者既考虑了小学生的心理特征，也考虑数学学科的特点，注意捕捉教学细节，通过制造精彩的认知冲突和分析比较，给学生指明探索的方向，激发学生探索的欲望，让学生充分利用已有知识经验去探索新的知识，成就高效的课堂。

四、合作探究，发展思维

1.探索梯形面积的计算公式

师：同学们，你们将平行四边形转化成长方形，将三角形转化成平行四边形，分别推导出了平行四边形和三角形的面积计算公式，我们要探索梯形的面积公式，你们想该怎么办？

（学生思考）

师：请同学们分小组合作，把你思考到的的方法告诉你的同桌，并且动手操作，等一下向全班同学汇报。

（学生4人小组合作探究，教师巡视指导。）

（让几个学生在展示仪上汇报展示操作情况。）

生1：可以用两个完全一样的梯形通过旋转、平移拼成一个平行四边形。

生2：用一个梯形，通过割补，拼成平行四边形。

生3：用一个梯形通过割补拼成三角形。

师：刚才同学们采用不同的割、拼方法，将梯形转化成平行四边形或三角形，分析了它们之间的关系。你们可以发现梯形面积的计算方法吗？

生：梯形面积=（上底+下底）×高÷2

师：上底加下底表示什么？乘高后又表示什么？为什么要除以2？

（学生根据不同的拼摆作出不同的回答）

生1：上底加下底表示拼成的平行四边形的底，再乘高得拼成的平行四边形的面积，最后除以2得梯形的面积。

生2：上底加下底表示拼成的平行四边形的底，再乘高除以2得平行四边形的面积，也就是梯形的面积。

生3：上底加下底表示拼成的三角形的底，再乘高除以2得三角形的面积，也就是梯形的面积。

师：如果用S表示梯形的面积，用a、b、h分别表示上、下底和高，你能用字母表示梯形的面积公式吗？

生：S=（a+b）×h÷2（板书）

2.分析

在学生合作操作前的细节中笔者适当指导，为学生指明思考方向，给予学生一定时间去探索，经历了梯形面积公式的精彩探索过程——S=（a+b）×h÷2，成就了高效率的课堂，培养了学生创新精神和探索抽象概括能力。

五、反思

在教学中，教师除了要为学生提供平等、宽松、自由的课堂氛围，还要做一名善意的的鼓励者和欣赏者，让课堂成为学生学习的乐园、充分表现和发挥个性才能的精彩舞台。而教师只要关注教学细节，就能成就高效的教学课堂。