迁移经验，提高“四能”

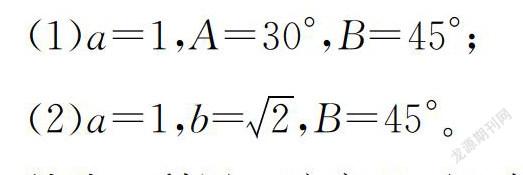
摘要：基本活动经验是指学生亲自或间接经历了活动过程而获得的经验，需要在“做”的过程中体验，在“思考”的过程中沉淀，是在数学学习活动过程中逐步积累的。形成和积累基本活动经验，是提高“四能”的有效手段，也是发展数学核心素养（“三会”）的基本方法。在教学过程中，教师要善于创设合适的问题情境，引导学生迁移已有的活动经验，发现、提出问题，并在新问题的分析、解决过程中不断积累新的活动经验，进而发展数学核心素养。以《正弦定理》第一课时为例加以说明。

关键词：基本活动经验学习迁移四能正弦定理

《普通高中数学课程标准（2017年版）》指出：通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验（简称“四基”）。基本活动经验是指学生亲自或间接经历了活动过程而获得的经验，需要在“做”的过程中体验，在“思考”的过程中沉淀，是在数学学习活动过程中逐步积累的。形成和积累基本活动经验，是提高“四能”的有效手段，也是发展数学核心素养（“三会”）的基本方法。在教学过程中，教师要善于创设合适的问题情境，引导学生迁移已有的活动经验，发现、提出问题，并在新问题的分析、解决过程中不断积累新的活动经验，进而发展数学核心素养。下面以苏教版高中数学必修5《正弦定理》第一课时为例，谈一些体会。

一、整体建构

用正弦定理解三角形，是初中解直角三角形的推广，故迁移解直角三角形的活動经验，用“化直”（包括借“高”化直和借“圆”化直）

的想法去研究，是一种自然的想法。另外，正弦定理的课程安排在“三角”“向量”知识之后，因此，借助向量的工具作用引入角，并研究几何问题，也是一种合适的选择。同时，用正弦定理解三角形，是典型的用代数的方法来解决几何问题，故解析法研究顺理成章。基于这样的学习经验，正弦定理的学习内容整体建构如图1所示。

二、教学设计

（一）创设情境，提出问题

导语法国数学家傅里叶有过这样的名言：对自然界的深刻研究是数学发现的最自然的来源。从金字塔的建造到尼罗河两岸的土地丈量，从大禹治水到都江堰的修建，从天文观测到精密仪器的制造……人们都离不开对几何图形的测量、设计和计算。

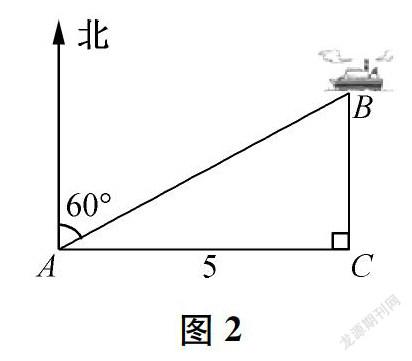
情境1小李骑车在长江边A处游玩，发现在他所在位置北偏东60°的B处，有一艘采沙船在江中作业。当他向正东方向骑行5千米到达C处后，发现该采沙船在他的正北方向（如图2）。

问题1你能就此情境提出一个数学问题吗？

情境2小李骑车在长江边A处游玩，发现在他所在位置北偏东60°的B处，有一艘采沙船在江中作业。当他向正东方向骑行5千米到达C处后，发现该采沙船在他的北偏西45°方向（如图3）。

问题2你能结合情境1的研究经验，提出一个数学问题，并研究一般结论吗？

设计意图：数学源于生活，依托一些生活实际问题，让学生用数学的眼光去观察、用数学的思维去分析、用数学的语言去表达，培养良好的数学素养。结合情境1，让学生主动思考、研究，培养学生发现问题、提出问题的能力。迁移情境1及问题1的基本活动经验，进一步研究情境2和问题2，让学生发现、提出数学问题，并探索、得出一般结论。这两个情境、问题是后续学生活动、数学建构的基础。

（二）学生活动，分析问题

活动1结合情境1和问题1，研究直角三角形的边角关系。

预设问题：在△ABC中，已知∠B=30°，∠C=90°，BC=5，求AB、AC的长。

本质揭示：本题实际是研究直角三角形的边角关系。

当△ABC是直角三角形时，假如∠C为直角，那么有sinA=ac，sinB=bc，sinC=1=cc。所以asinA=bsinB=csinC=c。

设计意图：活动1与情境1、问题1相呼应，研究直角三角形的边角关系，为推广研究一般三角形的边角关系做好准备。

活动2结合情境2和问题2，探索一般三角形的边角关系。

提出猜想：三角形的各边和它所对角的正弦之比相等，即asinA=bsinB=csinC。

画板验证：如图4。

推理论证：对于以上猜想，你能结合以往的学习经验，设计合适的研究方案尝试证明这一猜想吗？

1.方案探索。（1）转化为直角三角形中的边角关系（借“高”化直）;（2）建立直角坐标系，利用三角函数的定义（借“系”解形）;（3）通过外接圆，将任意三角形问题转化为直角三角形问题（借“圆”化直）;（4）利用向量的投影或者向量的数量积产生三角函数（借“箭”得角）。

2.严格论证。引导学生具体实施上述预设思路。

设计意图：在开放的活动中，引导学生经历“提出猜想—画板验证—推理论证（方案探索—严格论证）”等环节，感悟数学的严谨之美，并通过一题多证的方式，感受数学的开放之美;同时，培养学生分析、解决问题的能力。其中，方案探索的过程是唤醒并迁移已有活动经验的较高层次能力的表现。

（三）意义建构，感知数学

在学生活动的基础上，让学生规范表述正弦定理，理解正弦定理的文字语言、符号语言及常见变式（见上文图1）。

（四）数学运用，解决问题

例1小李骑车在长江边A处游玩，发现在他所在位置北偏东60°的B处，有一艘采沙船在江中作业。当他向正东方向骑行5千米到达C处后，发现该采沙船在他的北偏西45°方向。求 AB、AC的长。

说明一般地，我们把三角形的三个角和它的对边分别叫作三角形的元素。已知三角形的几个元素求其他元素的过程叫作解三角形。

例2根据下列条件解三角形。

（1）a=1，A=30°，B=45°;

（2）a=1，b=2，B=45°。

结论利用正弦定理可以解决的问题：（1）已知两边及其一条边的对角，求其他元素;（2）已知两角和一边，求其他元素。

练习请在横线上添加适当条件，并让同桌解答。

根据下列条件，解三角形。

设计意图：例1与情境2相呼应，即学即用，激发学生的学习兴趣。例2一方面帮助学生巩固所学，另一方面让学生及时总结，加深对正弦定理的认识，同时培养学生提出问题和解决问题的能力。

（五）回顾反思，理解数学

通过梳理重构，帮助学生整体建构知识结构（见上文图1）;通过对化归、分类讨论、数形结合等数学思想方法的感悟，让学生回归本真、理解数学;通过“你还能找到正弦定理的其他证明方法吗？”的拓展反思，将课堂延伸至课外，为培养学生的创新思维创设机会和平台。

（六）课外作业，巩固数学

必做题教材第9页练习1、2、3。

选做题在△ABC中，a=1，b=2，A=30°， 求B。

探究题尝试利用多种方法证明正弦定理。

三、教学反思

（一）活动经验是在学习过程中积累的

在数学教学中，数学活动的一个主要目的是让学生经历探究的过程、思考的过程、抽象的过程、预测的过程、推理的过程及反思的过程等，获取丰富的过程性知识，最终形成应用数学的意识。对于本节课，正弦定理的结论固然重要，但发现并证明定理的过程更加重要。学生在参与正弦定理发现、证明、应用的过程中所形成的感性知识、情绪体验和应用意识、创新意识等，即为数学活动经验。强调基本活动经验即强调数学学习过程。

（二）问题的提出与解决依托于活动经验的迁移

“发现问题—提出问题—分析问题—解决问题”是一个整体。问题发现、提出以后需要分析、解决，而在分析、解决的过程中又会不断地发现、提出新的問题。这种螺旋上升促进了研究的不断深入。作为教师，我们要在发现问题、提出问题中培养学生的“问题意识”。而这种意识则离不开已有经验的迁移作用。在正弦定理的学习过程中，问题的提出始终伴随着经验的迁移：在合适的情境中，迁移解直角三角形的经验，发现并提出问题;在得出猜想的基础上，依托以往的学习经验，提出研究方案，并尝试证明正弦定理。而在新问题的解决过程中，学生的学习经验又不断得以丰富、完善。

*本文系江苏省教育科学“十三五”规划重点资助项目“基于大数据分析的数学学习研究”（编号：Ba/2016/02/6）的阶段性研究成果。

参考文献：

[1] 范东晖.积累基本活动经验 发展数学核心素养[J].数学通报，2018（9）.

[2]张筱瑜，汪晓勤.“正弦定理”：用历史拓思维、润情感[J].教育研究与评论（中学教育教学），2015（6）.

[3]王新民，王富英，王亚雄.数学“四基”中“基本活动经验”的认识与思考[J].数学教育学报，2008（3）.

[4]曾荣.发现问题：一种创造性的思维活动[J].江苏教育，2018（9）.