线上线下合作促销的多渠道零售商微分动态策略研究
王军 牛志勇 黄沛




摘 要:本文針对多渠道零售商线上线下渠道进行合作促销的问题,构建了微分对策模型,运用最优控制理论分别求出分散式、集中式下的零售商最优促销努力投入、定价和利润。通过分析发现:1.在分散式决策下,两个渠道的努力程度先增加后下降;在集中式博弈下,两个渠道的努力程度始终上升;从短时间来看,不同渠道之间的努力程度相差无几,随着时间的增加,两者的努力程度相差逐渐增大;2.集中式决策下的零售商定价低于分散式决策下的定价;短期内分散式决策下的线上、线下利润会高于集中式博弈下的利润,但是随着时间增加集中式博弈下的利润会远远大于分散式决策下的利润;3.不同的销售努力相关参数对决策变量产生不同影响;状态变量的初始值对决策变量产生显著影响,不同的初始努力程度和增加销量,会改变决策变量的均衡时间路径。另外本文对渠道之间合作的讨价还价机制做了初步分析。
关键词:多渠道零售商;线上线下;联合促销;微分对策
中图分类号:F224
文献标识码:A
文章编号:1000-5099(2019)06-0043-11
Dynamic Differential Strategy for Multi ̄Channel Retailers Based on
Online ̄Offline Cooperative Promotion Efforts
WANG Jun1, NIU Zhiyong2, HUANG Pei3
(1. School of Management, Guizhou University,Guiyang, Guizhou,550025,China;2. Shanghai Development Research Institute, Shanghai
University of Finance Economics,Shanghai,200433,China;3. School of Management, Fudan University, Shanghai,200433,China)
Abstract:
Targeting on online ̄offline cooperative sales promotion of multi ̄channel retailers, this paper establishes ;differential strategy, applies optimal controlling theory, computing the optimal efforts, price and profits of promotion under integrated and decentralized decision models respectively. Through analysis, the results include: firstly, the efforts of two channels increase firstly and then decline under decentralized mode while maintain constant increase under integration; the efforts of different channels are similar in initial period but the longer the span of time is, the larger the difference of efforts in two channels becomes. Secondly, the prices of retailers under decentralization are lower than that under integration; the online and offline profits of retailers under decentralized game are larger than that under integrated game in short term, but as time extends, the profits under the integrated one are far more larger than the decentralized. Thirdly, different parameters related to promotion efforts can influence the decision variables; the initial values of state variables exert great influences on the decisive variables, with the equilibrium time ̄paths of decision changing with different promotion efforts and increase in sales Besides, this paper also gives a first step to study the mechanism of bargaining in cooperation between different channels.
Key words:
multi ̄channel retailer; online ̄offline; cooperative promotion; differential strategy
自线上渠道出现以来,其与传统渠道的竞争十分激烈,两个不同性质的渠道如何协同运作、降低竞争带来的损害是多渠道零售商本文的多渠道零售商指同时运营线下、线上渠道的零售商,如苏宁等。
面临的重要难题[1],多渠道零售商采取线下与线上合作促销成为一种市场趋势。[2]如“苏宁云商”在“双十一”促销活动中,提供线下体验、线上可享折扣的促销策略;另如银泰百货线上线下合作促销,采取线下体验、线上可享折扣,消费者可以选择在线下或线上购买同一线下零售商的产品。多渠道零售商希望打破不同性质渠道冲突的局面,从而获得线上线下的合作共赢。与此同时,这些多渠道零售商也面临着“集中”决策和“分散”决策的问题,即其需要从整体或者局部来最大化自己的利润,如前者“苏宁云商”以线上线下整合为目标从而采取类似于“集中式”的决策。而银泰百货将线上线下隔离,各自为利润中心,这类似于“分散式”决策。这两种模式对多渠道零售商销售的影响尚存疑问。
一方面,虽然线上零售市场占有率增长较快,但与线下市场份额来比还是较低的,同时他们需要建立与消费者的直接沟通,使消费者更容易接受其销售的产品;另一方面,线下实体店也在寻求与线上合作的机会,进而扩展自身的销售领域。进一步判断,渠道的需求是与销售方式和努力程度相关联的。Tsay和Agrawal[3]认为渠道的需求是销售努力的递增函数,两个渠道的共同销售努力会产生正的网络外部性,提升零售商的整体需求,[4]即线上线下零售商通过销售合作,有利于实现渠道的优势互补,提升总体需求,零售商之间可以共享增加的收益。
那么由此派生出来的相关问题是:多渠道零售商又该如何进行线上线下渠道的促销努力合作决策?不同渠道的产品定价、利润、促销努力是否会随着时间变化而变化?增加的渠道需求如何在零售商之间进行分配?不同的决策形式(集中和分散)如何影响零售商的收益?这些问题对多渠道零售商来讲显得至关重要。
本文将以微分博弈的方法寻找多渠道零售商线下线上渠道促销合作的动态均衡策略。在假设合作销售下两个零售商会增加额外的销量的前提下,将该销量作为状态函数,在此基础上建立微分博弈方程探讨两者的动态均衡。将微分博弈方法应用到线上线下渠道销售合作中,从动态的角度考虑线上线下零售商的合作问题,具有一定的理论价值。
一、相关文献回顾
和本文相关的研究有以下三类:
一是传统零售商之间的合作问题研究。如李昌文等[5] 基于两层分销供应链系统,运用两阶段博弈模型研究了零售商联盟合作及稳定性的条件;Raju和Zhang[6]研究了在占优零售商存在下,零售商之间的合作问题。Li等[7]研究了制造商开辟直销渠道参与市场的情况,考虑制造商的公平关注以及与零售商的合作策略对零售商以及渠道绩效的影响;Melis等[8]基于消費者角度研究了线上线下双渠道消费者购买份额的变化;Hua等[9]研究了在供应链体系中,不同零售商之间的合作价格决策。上述这些研究从价格、广告、库存、物流等角度研究了零售商之间的合作,但都集中于传统零售商之间的合作。
二是线下渠道与线上渠道的竞争模型研究,主要关注了线上渠道出现后,线下渠道如何与之竞争。Balasubramanian[10]首先从理论模型的角度研究了包含线下零售商和单纯网络零售商的渠道中,零售商如何选择最优的价格竞争策略。Liu等[11]研究了传统零售商开辟网络渠道是对纯粹的互联网分销商的一个制约,并给出了相应的协调策略。Weon Sang Yoo等[12]研究了不同渠道结构下的线上线下零售商的竞争问题。另外一系列研究关注了制造商开辟线上渠道如何与线下渠道竞争,如Chiang等[13]利用博弈模型研究了当制造商采取直销模式时,传统零售商的应对价格策略。
同时也有学者关注了多渠道零售商如何开展线下渠道与线上渠道的合作模型研究,基本上以静态模型为主。Zhang[14]研究了线上线下零售商网络渠道的价格—广告合作策略,他们通过静态的Hoteling模型研究发现:在竞争环境下互联网渠道对线下产品进行价格广告宣传是一种均衡策略。Kollmann[15]认为跨渠道的合作可以使线上线下企业融合他们的商业模式,降低之间的竞争。Zhang等[16]认为线上线下渠道的合作可以提升消费者对品牌的忠诚,从而给双方企业带来正面效应。Dinner等[17]研究认为线上线下的交叉广告可以提升双方的利润。类似的研究还包括了Pauwels和Neslin[18]以及Cao 和Li等[19],认为线上线下渠道合作是不可阻挡的趋势,会给企业带来不同的交叉效应。另外的一些研究,如Fruchter和Tapiero[20]从动态的角度研究了直销渠道和线上渠道的合作,他们更多的是从消费者的购买可能性角度进行了分析。整体上讲,目前缺乏对线上线下合作的动态研究。
三是微分动态的博弈研究。营销中对微分动态的研究集中于合作广告和渠道方面,如Jorgensen[21]、Karray和Martin-Herran[22]等对零售商的动态合作广告进行了模型分析。陈东彦等[23]运用微分对策模型研究了广告延迟时间对供应链最优广告策略及决策机制的影响,其他研究集中在了合作库存等方面,如Zhou等[24]研究了在部分信息下的联合定价和库存合作问题;Martin-Herran[25]利用微分对策模型研究了零售商的动态定价和渠道协调的问题,他将传统的对渠道协调的静态研究拓展到了动态环境。虽然微分动态模型能够较好地刻画零售商之间的合作问题,但是较少应用到描述线上和线下渠道之间的问题,本文希望在这些方面有所突破。
综上,本文将以动态视角分析多渠道零售商线上线下渠道合作促销努力下各自的最优价格和努力决策。首先,运用微分动态理论建立线上线下渠道合作销售的博弈模型,并探讨分散式和集中式两种决策形式的最优解;其次,比较、分析不同形式下的最优价格和努力投入随时间的变化,得出渠道之间的最优策略;最后,讨论了如何分配联合促销努力获得的需求,进而获得可行的帕累托最优合作方案。本文期望所得到的相关结论为多渠道零售商在销售合作、融合发展等方面的科学决策提供理论依据。
二、模型与基本假设
考虑市场上包含一个线下渠道R和一个线上渠道N的多渠道零售商M,销售同一产品给所有消费者,其决定线上线下渠道共同采取促销活动。为了确定两个渠道的需求函数,本文参考Chiang等[13]的假设分析,其认为消费者对线下渠道和线上渠道的产品购买效用分别为v-pR和δv-pN,其中v是产品带给消费者的效用,0<δ<1是消费者对线上渠道的接受程度,Liang和Huang[26]、Kacen等[27]都证明了该参数的存在性。在该假设下,当v-pR≥δv-pN时,消费者会在线下购买,反之会在线上购买,当然两者的效用都要大于0。根据这样的假设分析计算,在静态状态下可以得到两者的需求函数具有Ai-Bipi+Cipj的线性形式,其中i、j分别为R和N。其中AR和AN表示了当两个渠道价格均为0时的最大需求,并且AR>AN,这是由于有δ存在的原因。该线性需求模式也被Chiang 等[13]以及Yue和Liu[28]所认可,牛志勇等[29]运用Bowley模型针对线上线下需求也给出了类似的线性需求函数形式,同时根据价格效应的不对称性,上述需求函数满足Bi>Ci。
本文基于上述线性需求函数,为了简化处理接下来的求解过程,在没有促销努力下,对线下零售商的需求函数Q′R和线上零售商的需求函数Q′N作如下假设:
Q′R=1-pR+bpN Q′N=a-pN+bpR(1)
其中0<b<a<1。a表示了消费者对线上渠道的接受程度(a是δ的函数)。根据前文分析,假设消费者对线上渠道的接受程度小于线下渠道的,于是0<a<1,当然也可以按照Dixit[30]等的理解为当所有价格为0时,线上的需求小于线下,这和现实情况也较为吻合。b可以理解为两者价格替代参数,根据Singh和Vives[31]的假设,令0<b<a。
如果两个渠道确定对某产品销售合作努力,在时刻t的销售努力程度分别为sR(t)和sN(t),其目的是为了将消费者保留在原有渠道中,例如线下派更多的销售人员进行产品销售,线上提升图片的展示效果等。在两个渠道销售努力下,根据Tsay和Agrawal[3]以及Rubel和Zaccour[32]的相关设定,产品市场会依据销售努力产生额外销售q(t),并且該额外需求由该两个渠道努力程度确定,即时刻t需求q(t)由sR(t)和sN(t)影响的状态变量,假定有下面表达式:
dq(t)dt=q·(t)=f(sR(t),sN(t)),q(0)=q0>0(2)
根据Rubel和Zaccour、Zhou和Lin的相关研究,本文假定f(·)为线性函数,具体表达式为f(sR(t),sN(t))=αRsR(t)+αNsN(t)-δq(t),其中αi为渠道i促销努力的效率系数,即努力对销量增加的边际,αRsR(t)+αNsN(t)反映出促销努力对销售额增加的影响,δ为衰减系数
在需求与广告投入的微分方程研究中(如陈东彦等[23])考虑到广告的协同作用,而并未考虑,将广告效应独立分析;而在渠道相关的研究中,Rubel和Zaccour[32]、Pauwels和Neslin[18]均对渠道间的努力效应进行独立处理,认为线上线下的促销努力具有一定的独立性,可不考虑协同影响效用,本文为简化相关运算,选择与上述文献类似的处理。。结合(1)和(2)得到两个零售商在合作销售努力下时间t的需求函数分别为:
QR(t)=1-pR(t)+bpN(t)+γ(q(t))
QN(t)=a-pN(t)+bpR(t)+(1-γ)(q(t))(3)
其中0<γ<1为两者对增加需求量的分配比例,根据Tasy和Agrawal[3]、Fruchter 和Tapiero[20]以及 Rubel和Zaccour[32]均认为需求 q(t)在两个渠道之间会进行分配,但该系数可能由多种因素确定,如渠道之间的权利对比。本文首先考虑该参数为外生的情况,其后会再讨论两者通过讨价还价的方式决定销量的分配。同时假定两个零售商的销售努力成本是凸递增的,为简化起见,采用二次函数形式,成本函数表达式如下:
ci(si)=12cisi2,ci>0,i∈{R,N}(4)
其中ci为渠道i努力程度的边际成本系数,其越高表示零售商付出的成本越高。
文中主要变量描述如表1所示:
综上,可以得到两者的利润函数及相关决策变量,每个渠道分别面临价格和合作销售努力的决策,如果考虑无限期的决策函数,假设市场贴现率为r,于是得到目标函数分别为:
MaxpR,sR∏R=∫SymboleB@
0[pR·(1-pR(t)+bpN(t)+γq(t))-12cRsR2]·e-rtdt
MaxpN,sN∏N=∫SymboleB@
0{pN·[a-pN(t)+bpR(t)+(1-γ)q(t)]-12cNsN2}·e-rtdt
s.t.
q·(t)=αRsR(t)+αNsN(t)-δq(t),q(0)
=q0≥0(5)
三、不同决策模式下的结果分析
1.分散式决策
在分散式决策下,多渠道零售商将决策权分别赋予线上线下渠道,线下渠道R和线上渠道N以自己利润最大为目标,即方程(5)为最优求解问题。根据博弈结构,两者进行水平无限期决策,所以假设两者采用正反馈促销努力决策,结果关注于两者的平稳性策略,即需求出正反馈纳什均衡,根据Pontryagin等[33]的动态最优化理论,方程(5)的最优值即如下Hamilton方程组的最优值:
HR=pR·(1-pR+bpN+γq)-12cRsR2+λR(αRsR+αNsN-δq)(6)
HN=pN·[a-pN+bpR+(1-γ)q]-12cNsN2+λN(αRsR+αNsN-δq)(7)
其中λi為联合状态函数,并且满足条件λ·i=rλi-Hiqi=(R,N) 。根据最优解的必要条件,对Hamilton函数分别求导,有下面的公式:
HpRR=HRpR=1-2pR+bpN+γq=0(8)
HsRR=HRsR=-cRsR+λRαR=0(9)
HpNN=HNpN=a-2pN+bpR+(1-γ)q=0(10)
HsNN=HNsN=-cNsN+λNαN=0(11)
由(8)和(10)可以得到:
pR=(2+ab)+(b+2γ-bγ)q4-b2(12)
pN=(2a+b)+(2+bγ-2γ)q4-b2(13)
从(12)和(13)可以看到两个渠道的定价与新增销量q有关系,并且随着q增加而增加,说明当双方合作努力增加产品市场销售时,双方的最优定价是q的递增函数,增加的销量给两个渠道带来额外利润,零售商从中获益。另外根据γ取值大小,给出下面引理:
引理1:在时刻t,线下零售商价格pR大于线上零售商价格pN需满足条件:
(1)γ≥12,或者
(2)0<γ<12并且q(t)≤1-a1-2γ
引理1显示,联合促销带来的额外销量有一半以上分配给线下零售商;或当增加的销量较少时,线下零售商的价格高于线上零售商,反之则低。从分析来看,线上和线下零售商的定价差异会受到多方面因素的影响,当双方有销售努力付出时,应该根据自己能够获得的收入而调整销售价格,此时线上零售商的价格可能高于线下零售商。
再将(12)和(13)分别带入(6)和(7)中,可以得到λR和λN满足以下公式:
λ·R=(r+δ)λR-2(b+2γ-bγ)(2+ab+2γq+bq-bγq)(4-b2)2(14)
λ·N=(r+δ)λN-2(2+bγ-2γ)(2a+b+2q+bγq-2γq)(4-b2)2(15)
再根据(9)和(11)有:
sR=αRcRλR,sN=αNcNλN(16)
公式(16)显示了渠道的促销努力程度是Hamilton方程因子的线性函数,并且与成本系数、效率系数相关。综合(12)、(13)、(14)、(15)和(16)可以得到下面结论:
结论1:时刻t,多渠道零售商分散决策下,线下渠道和线上渠道的最优定价pDR和pDN、最优促销努力程度sDR和sDN满足下面关系:
pDR=(2+ab)+(b+2γ-bγ)q4-b2
pDN=(2a+b)+(2+bγ-2γ)q4-b2
s·DR=rsDR-2αR(b+2γ-bγ)(2+2γq+bq+ab-bγq)cR(4-b2)2(17)
s·DN=rsDN-2αN(2+bγ-2γ)(2a+2q+b+bγq-2γq)cN(4-b2)2(18)
q·=αRsDR+αNsDN-δq,q(0)=q0≥0
上述微分方程组具有显性解,但由于参数较多,解的表达式十分复杂,将在下节进行数值模拟呈现,进而确定双方的最优决策。
2.集中式决策
集中式决策意味着两个渠道的分散决策变为集中式下的一个决策者,如“苏宁云商”的整合渠道管理,由公司总部统一决定两个渠道的相关决策,于是两个渠道可进行整合策略决定,多渠道零售商的最优问题为:
MaxpR,pN,sR,sN∏=∫SymboleB@
0{pR·(1-pR(t)+bpN(t)+γq(t))+pN·[a-pN(t)+bpR(t)+(1-γ)q(t)]-12cNsN2-12cRsR2}·e-rtdt
s.t.
q·(t)=αRsR(t)+αNsN(t)-δq(t),q(0)
=q0≥0(19)
于是Hamilton方程为:
H=pR·(1-pR+bpN+γq)+pN·[a-pN+bpR+(1-γ)q]-12cNsN2-12cRsR2+λ(αRsR+αNsN) (20)
其中λ为联合状态函数,满足λ·=rλ-Hq ,根据最优解的必要条件,满足下面等式:
HpR=HpR=1-2pR+2bpN+γq=0(21)
HsR=HsR=-cRsR+λαR=0(22)
HpN=HpN=a-2pN+2bpR+(1-γ)q=0(23)
HsN=HsR=-cNsN+λαN=0(24)
有(21)和(23)可知:
pCR=(1+ab)+(b+γ-bγ)q2(1-b2)(25)
pCN=(a+b)+(1+bγ-γ)q2(1-b2)(26)
比较(12)、(13)、(25)和(26)可知下面引理:
引理2:在时刻t,合作博弈下零售商价格高于非合作博弈下的价格,也即有pCR>pDR和pCN>pDN。
从引理2可以看出,合作博弈降低了不同性质渠道之间的价格竞争,线上和线下价格有所上升。如果從零售商的利润来看,整体利润将会有所提升,该引理的相关结论在数值模拟中可以给予更加明显的证明。
再比较(22)和(24)可知,有下面引理:
引理3:在时刻t,不同渠道之间的销售努力满足下面公式:
sRsN=αRcR/αNcN(27)
公式(27)显示,渠道i的相对努力程度与相关效率αi/ci相关,该效率值越高,渠道的努力程度相对越高,在此条件约束下,销售努力会更有效。
将(25)和(26)带入(20)可以得到联合状态变量满足下面关系:
λ·=(r+δ)λ-a+b+γ+abγ-aγ-bγ2(1-b2)-1+2γ2+2bγ-2bγ2-2γ2(1-b2)q(28)
根据上述求解,可以得到下面结论:
结论2:时刻t在合作博弈下,线下零售商和线上零售商的定价、合作销售努力程度满足下面关系式:
pCR=(1+ab)+(b+γ-bγ)q2(1-b2)
pCN=(a+b)+(1+bγ-γ)q2(1-b2)
s·CR=λsCR-αRcR[a+b+γ+abγ-aγ-bγ2(1-b2)+1+2γ2+2bγ-2bγ2-2γ2(1-b2)q](29)
s·CN=λsCN-αNcN[a+b+γ+abγ-aγ-bγ2(1-b2)+1+2γ2+2bγ-2bγ2-2γ2(1-b2)q](30)
结论1和结论2表示了在联合促销努力下,不同博弈情况满足了不同的微分方程条件,两者满足的方程在一定初值条件下具有解析解,即存在使得利润最优的决策变量(价格与努力程度)。为了更加直观地分析各决策变量依据时间路径(针对t)的均衡,本文用数值模拟分析相关结果,并对结果进行对比分析。
四、结果对比与数值模拟
由于结论1和结论2求解较为复杂,为简单起见,本文将固定相应参数进行数值分析,从而能更明晰地判断多渠道零售商的不同决策。为了达到效果,假设相关参数取值如表2。假定两个渠道的努力效率系数相同(αR=αN);线下渠道的边际成本更高(cR>cN),即付出相同的努力成果,线下渠道需要花费更高的成本,这是针对线下门店的运营成本高于线上的这一现状而假设;同时假定线下渠道获取更高的增加销量(γ>0.5),而关于这一系数,会在下节进行专门讨论。由于动态抉择中考虑到了连续的时间,为了较为清楚地观测到策略的动态变化,数值模拟中将时间t取值设为区间[0,3.5]。
1.联合促销努力程度的决策对比
根据结论1与结论2,需通过求解微分方程组可得零售商最优努力程度解析式,将表2的参数带入求解,分别可以得到:
sDR=0.34e0.05tsin(0.29t)+5.60e0.05tcos(0.29t)-0.52e0.10t-0.085(31)
sDN=0.27e0.05tsin(0.29t)+4.40e0.05tcos(0.29t)+0.52e0.10t+0.085(32)
sCR=0.58e0.10t+1.80e0.70t+2.50e-0.60t+0.91(33)
sCN=2.30e0.70t+3.10e-0.60t-0.58e0.10t-0.91(34)
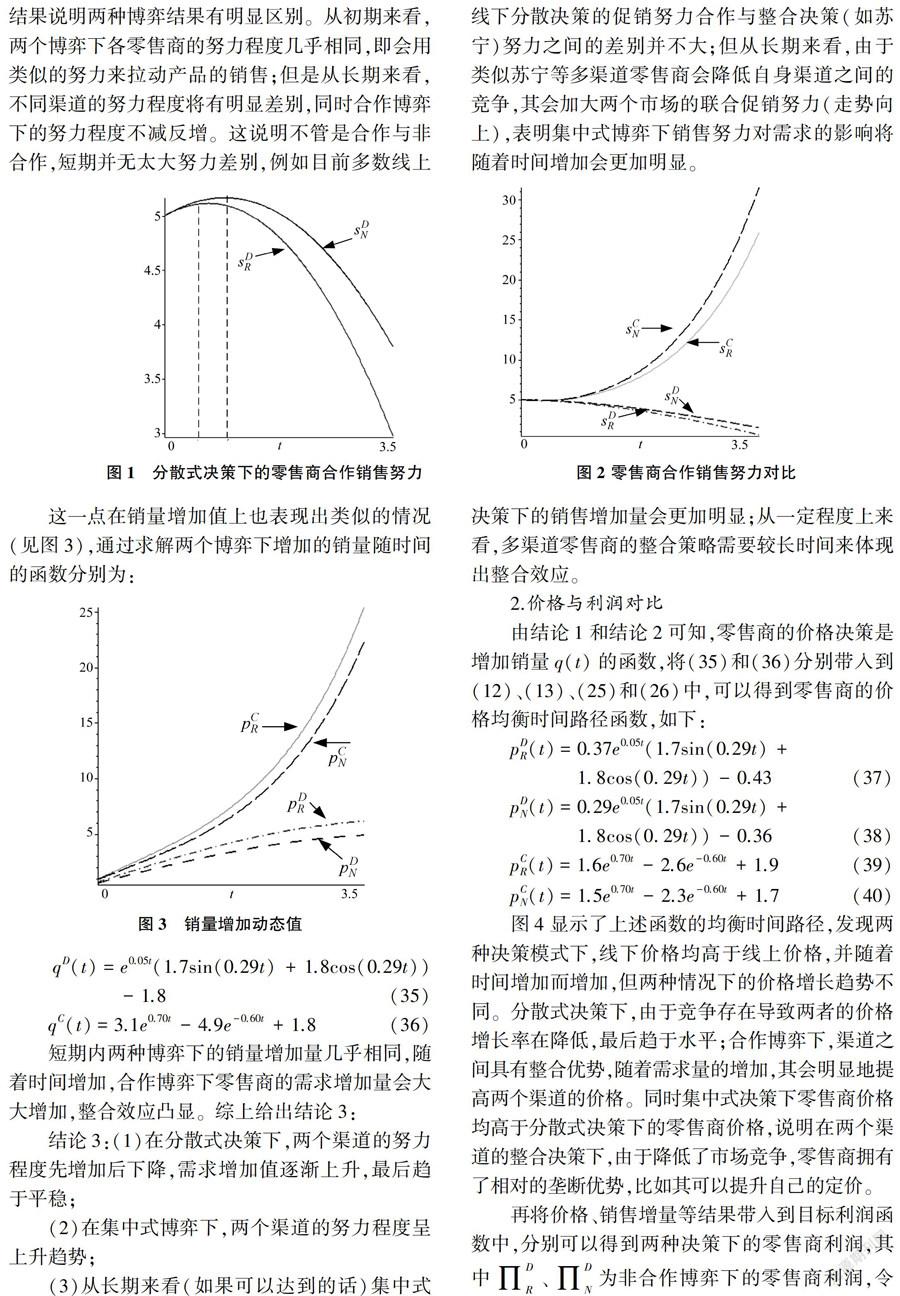
从上述结果可以明显看到sDN>sDR,并且有sCRt>0和sCNt>0,即在分散式决策下,线上渠道将会付出更多的努力,在合作博弈下努力程度会随着时间增加而增加,图1和图2给出了更为清楚的努力程度的均衡时间路径。图1显示了sDN和sDR的均衡时间路径,在分散式决策下两零售商的努力程度初期会增加,达到最大值后逐渐下降,并且线上零售商的努力程度高于线下零售商的努力程度。这说明在促销初期,由于销售努力带来了额外销量,双方会逐渐提升合作销售的努力程度,而当努力增长到一定程度后,开始下降。究其原因,这一方面和竞争相关,另一方面随着时间的增加,增加的销量会逐渐趋于平稳(见图3),带来的额外利润会被努力付出的成本抵消,于是逐渐降低努力付出。同时线下渠道会比线上渠道提前开始减少努力付出(t1<t2,其中sDR(t1)t=0,sDN(t2)t=0)。
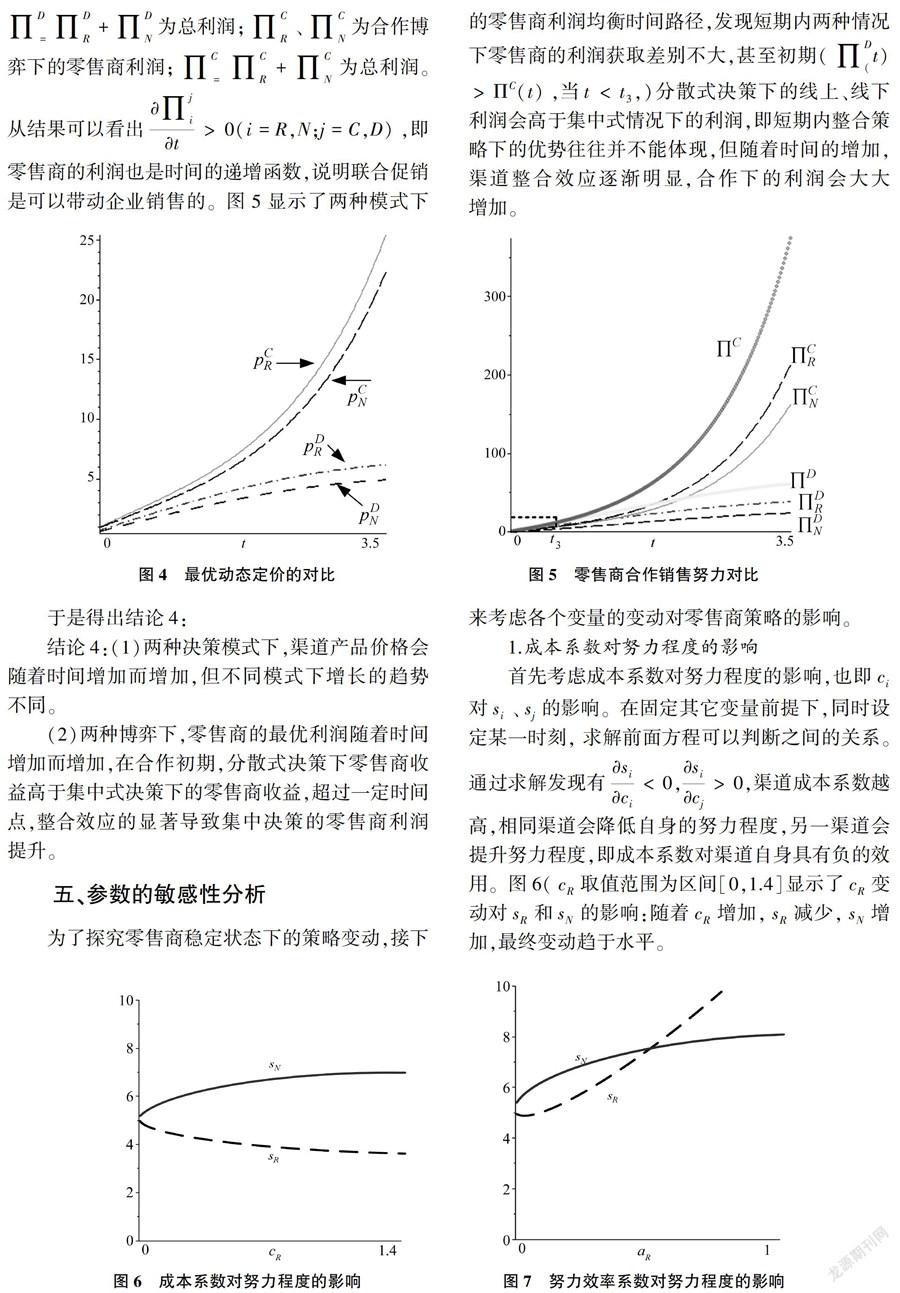
图2显示了两种决策模式下的努力程度对比,结果说明两种博弈结果有明显区别。从初期来看,两个博弈下各零售商的努力程度几乎相同,即会用类似的努力来拉动产品的销售;但是从长期来看,不同渠道的努力程度将有明显差别,同时合作博弈下的努力程度不减反增。这说明不管是合作与非合作,短期并无太大努力差别,例如目前多数线上线下分散决策的促销努力合作与整合决策(如苏宁)努力之间的差别并不大;但从长期来看,由于类似苏宁等多渠道零售商会降低自身渠道之间的竞争,其会加大两个市场的联合促销努力(走势向上),表明集中式博弈下销售努力对需求的影响将随着时间增加会更加明显。
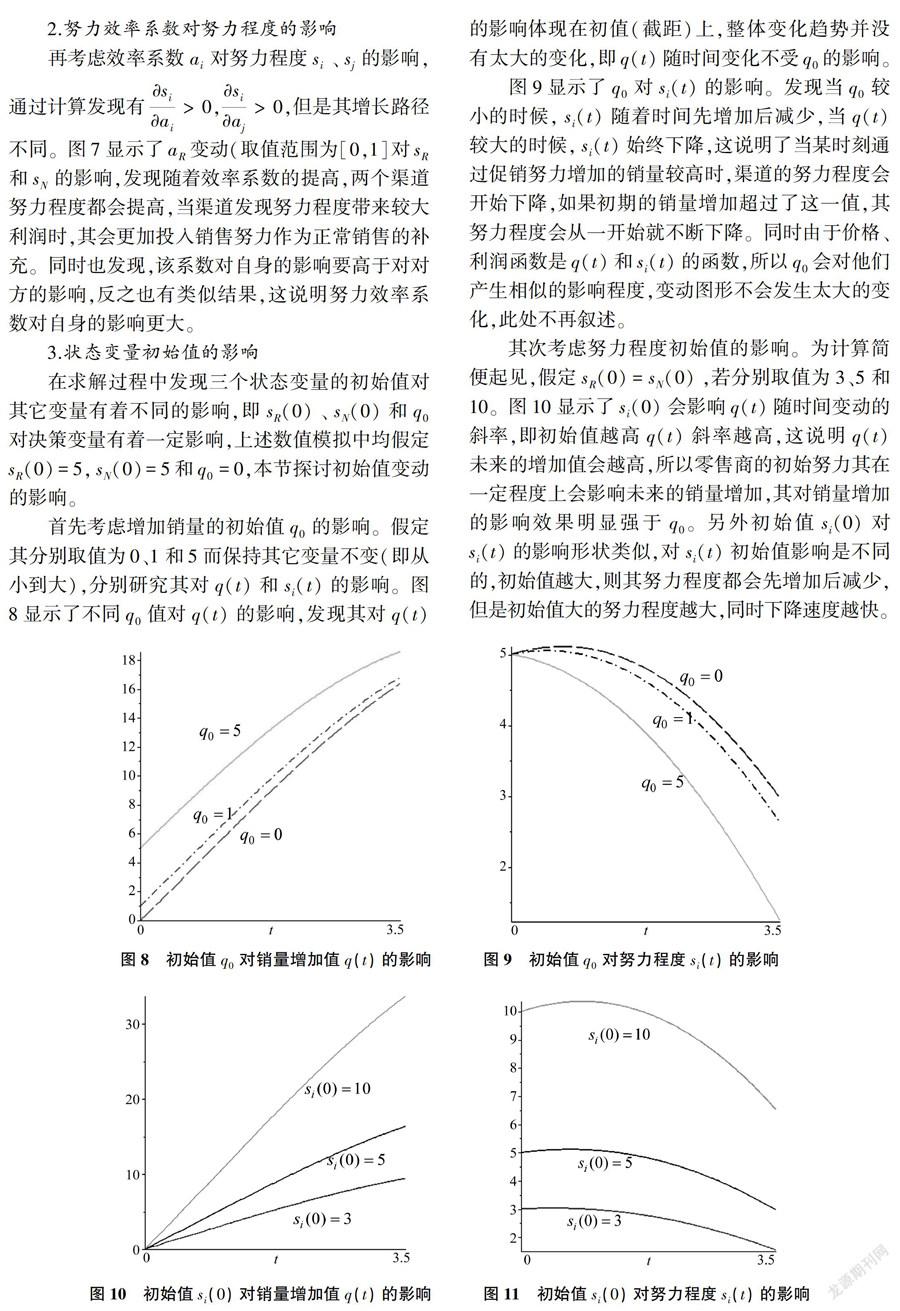
这一点在销量增加值上也表现出类似的情况(见图3),通过求解两个博弈下增加的销量随时间的函数分别为:
qD(t)=e0.05t(1.7sin(0.29t)+1.8cos(0.29t))-1.8(35)
qC(t)=3.1e0.70t-4.9e-0.60t+1.8(36)
短期内两种博弈下的销量增加量几乎相同,随着时间增加,合作博弈下零售商的需求增加量会大大增加,整合效应凸显。综上给出结论3:
结论3:(1)在分散式决策下,两个渠道的努力程度先增加后下降,需求增加值逐渐上升,最后趋于平稳;
(2)在集中式博弈下,两个渠道的努力程度呈上升趋势;
(3)从长期来看(如果可以达到的话)集中式决策下的销售增加量会更加明显;从一定程度上来看,多渠道零售商的整合策略需要较长时间来体现出整合效應。
2.价格与利润对比
由结论1和结论2可知,零售商的价格决策是增加销量q(t)的函数,将(35)和(36)分别带入到(12)、(13)、(25)和(26)中,可以得到零售商的价格均衡时间路径函数,如下:
pDR(t)=0.37e0.05t(1.7sin(0.29t)+18cos(029t))-0.43(37)
pDN(t)=0.29e0.05t(1.7sin(0.29t)+18cos(029t))-0.36(38)
pCR(t)=1.6e0.70t-2.6e-0.60t+1.9(39)
pCN(t)=1.5e0.70t-2.3e-0.60t+1.7(40)
图4显示了上述函数的均衡时间路径,发现两种决策模式下,线下价格均高于线上价格,并随着时间增加而增加,但两种情况下的价格增长趋势不同。分散式决策下,由于竞争存在导致两者的价格增长率在降低,最后趋于水平;合作博弈下,渠道之间具有整合优势,随着需求量的增加,其会明显地提高两个渠道的价格。同时集中式决策下零售商价格均高于分散式决策下的零售商价格,说明在两个渠道的整合决策下,由于降低了市场竞争,零售商拥有了相对的垄断优势,比如其可以提升自己的定价。
再将价格、销售增量等结果带入到目标利润函数中,分别可以得到两种决策下的零售商利润,其中∏DR、∏DN为非合作博弈下的零售商利润,令∏D=∏DR+∏DN为总利润;∏CR、∏CN为合作博弈下的零售商利润;∏C=∏CR+∏CN为总利润。从结果可以看出∏jit>0(i=R,N;j=C,D),即零售商的利润也是时间的递增函数,说明联合促销是可以带动企业销售的。图5显示了两种模式下的零售商利润均衡时间路径,发现短期内两种情况下零售商的利润获取差别不大,甚至初期(∏D(t)>ΠC(t),当t<t3,)分散式决策下的线上、线下利润会高于集中式情况下的利润,即短期内整合策略下的优势往往并不能体现,但随着时间的增加,渠道整合效应逐渐明显,合作下的利润会大大增加。
于是得出结论4:
结论4:(1)两种决策模式下,渠道产品价格会随着时间增加而增加,但不同模式下增长的趋势不同。
(2)两种博弈下,零售商的最优利润随着时间增加而增加,在合作初期,分散式决策下零售商收益高于集中式决策下的零售商收益,超过一定时间点,整合效应的显著导致集中决策的零售商利润提升。
五、参数的敏感性分析
为了探究零售商稳定状态下的策略变动,接下来考虑各个变量的变动对零售商策略的影响。
1.成本系数对努力程度的影响
首先考虑成本系数对努力程度的影响,也即ci对si、sj的影响。在固定其它变量前提下,同时设定某一时刻,求解前面方程可以判断之间的关系。通过求解发现有sici<0,sicj>0,渠道成本系数越高,相同渠道会降低自身的努力程度,另一渠道会提升努力程度,即成本系数对渠道自身具有负的效用。图6(cR取值范围为区间[0,1.4]显示了cR变动对sR和sN的影响:随着cR增加,sR减少,sN增加,最终变动趋于水平。
2.努力效率系数对努力程度的影响
再考虑效率系数ai对努力程度si、sj的影响,通过计算发现有siai>0,siaj>0,但是其增长路径不同。图7显示了aR变动(取值范围为[0,1]对sR和sN的影响,发现随着效率系数的提高,两个渠道努力程度都会提高,当渠道发现努力程度带来较大利润时,其会更加投入销售努力作为正常销售的补充。同时也发现,该系数对自身的影响要高于对对方的影响,反之也有类似结果,这说明努力效率系数对自身的影响更大。
3.状态变量初始值的影响
在求解过程中发现三个状态变量的初始值对其它变量有着不同的影响,即sR(0)、sN(0)和q0对决策变量有着一定影响,上述数值模拟中均假定sR(0)=5,sN(0)=5和q0=0,本节探讨初始值变动的影响。
首先考虑增加销量的初始值q0的影响。假定其分别取值为0、1和5而保持其它变量不变(即从小到大),分别研究其对q(t)和si(t)的影响。图8显示了不同q0值对q(t)的影响,发现其对q(t)的影响体现在初值(截距)上,整体变化趋势并没有太大的变化,即q(t)随时间变化不受q0的影响。
圖9显示了q0对si(t)的影响。发现当q0较小的时候,si(t)随着时间先增加后减少,当q(t)较大的时候,si(t)始终下降,这说明了当某时刻通过促销努力增加的销量较高时,渠道的努力程度会开始下降,如果初期的销量增加超过了这一值,其努力程度会从一开始就不断下降。同时由于价格、利润函数是q(t)和si(t)的函数,所以q0会对他们产生相似的影响程度,变动图形不会发生太大的变化,此处不再叙述。
其次考虑努力程度初始值的影响。为计算简便起见,假定sR(0)=sN(0),若分别取值为3、5和10。图10显示了si(0)会影响q(t)随时间变动的斜率,即初始值越高q(t)斜率越高,这说明q(t)未来的增加值会越高,所以零售商的初始努力其在一定程度上会影响未来的销量增加,其对销量增加的影响效果明显强于q0。另外初始值si(0)对si(t)的影响形状类似,对si(t)初始值影响是不同的,初始值越大,则其努力程度都会先增加后减少,但是初始值大的努力程度越大,同时下降速度越快。
综上,状态变量的初始值不仅会影响到决策变量的初始值变化,也会影响到未来的时间路径走势,所以当线上和线下零售商确定要进行销售合作时,要根据对未来的利润需求合理分配初始的努力投入。
六、结论
本文利用微分对策理论研究了多渠道零售商的线上线下渠道联合促销努力的决策问题,针对分散式和集中式决策模式得到了不同模型下的零售商最优努力、价格和各自利润等相关决策。具体结论如下:
1.多渠道零售商线上线下渠道进行联合促销时,两个渠道的最优定价与联合促销努力带来的销售增量相关,并且在一般情况下,线下价格高于线上价格;分散式决策下的定价低于集中式决策下的情况,合作博弈降低了零售商之间的竞争;
2.线上线下渠道的最优努力程度在不同决策模式下有不同的均衡最优时间路径。分散式决策下,两个渠道的努力程度先增加后下降;集中式决策下,两个渠道的努力程度始终上升;从短时间来看,不同渠道之间的努力程度相差无几,随着时间的增加,两者的努力程度相差逐渐增大;
3.两种决策模式下零售商的利润变化也不同。短期内,分散式决策下的线上线下利润会高于集中式决策下的利润,随着时间增加,集中式决策下的利润会明显大于分散式决策下的;零售商的成本系数对其销售努力付出有负向影响,对其他零售商有正向影响,成本系数阻碍本身的努力付出;努力效率系数对努力程度有着正向影响,但该系数对自身的影响要高于对对方的影响。
4.如果通过讨价还价进行增加销量(利润)的分配,先出价者具备先动优势,在同等水平下可以获得更高的分配份额。从分析来看,零售商的最优定价与该分配比例相关,线下渠道会根据比例进行定价,研究发现当分配比例低于一半时,其价格可能会低于线上渠道。
依据上述结论,本文对多渠道零售商整合决策有所建议,并从动态的角度对未来的最优决策进行了预测。从目前来看,多渠道零售商一直在倡导线上线下渠道的融合,本文从两个渠道进行联合促销给予建议:从短期来看,线上线下融合发展(集中式决策)并未起到明显的作用,但是随着两个渠道交互效应的逐步显现,长期来看,不同渠道的整合发展能够给多渠道零售商带来较大的增长效应。所以,本文结论支持了多渠道零售商进行整合发展的相关战略决策。
本文结论是在一定假设下得到的,推广应用尚需进一步实证证明。针对不足,后续的研究方向可包括:(1)研究供应商存在下的多层渠道结构下的销售合作,重点探讨渠道协调的问题;(2)放松本文模型的假设,能从一般解析解的角度或者理论解析的角度进行分析;(3)针对合作分配做进一步细致的探讨,寻找讨价还价机制。
参考文献:
[1]WALLACE D W, GLIESE J L, JOHNSON J L. Customer Retailer Loyalty in the Context of Multiple Channel Strategies [J]. Journal of Retailing, 2004, 80(4): 249-263.
[2]WEI HUANG, JAYASHANKAR M. Introduction of a Second Channel: Implications for Pricing and Profits [J]. European Journal of Operational Research, 2009, 194(1):258-279.
[3]TSAY A A, AGRAWAL N. Channel Conflict and Coordination in the E ̄commerce Age [J]. Production and Operations Management, 2004, 13(1): 93-110.
[4]LAN Y, LI Y, PAPIER F. Competition and Coordination in a Three ̄tier Supply Chain with Differentiated Channels[J]. European Journal of Operational Research, 2018, 269(3): 870-882.
[5]李昌文, 周永務, 郭金森,等. 两层供应链中数量竞争下零售商联盟合作及稳定性研究[J]. 系统管理学报, 2018(4):194-203.
[6]RAJU J, ZHANG Z J. Channel Coordination in the Presence of a Dominant Tetailer [J]. Marketing Science, 2005, 24(2): 254-262.
[7]LI B, HOU P W, LI Q H. Cooperative Advertising in a Dual ̄channel Supply Chain with a Fairness Concern of the Manufacturer[J]. IMA Journal of Management Mathematics, 2015, 28(2): 259-277.
[8]MELIS K, CAMPO K, LAMEY L, et al. A Bigger Slice of the Multichannel Grocery Pie: When Does Consumers’ Online Channel Use Expand Retailers’ Share of Wallet?[J]. Journal of Retailing, 2016, 92(3): 268-286.
[9]HUA G W, WANG S Y, CHENG T C. Price and Lead Time Decisions in Dual ̄channel Supply Chains [J]. European Journal of Operation Research, 2010, 205(1): 113-126.
[10]BALASUBRAMANIAN S. Mail Versus Mall: A Strategic Analysis of Competition Between Direct Marketers and Conventional Retailers [J]. Marketing Science, 1998, 17(3): 181-195.
[11]LIU Y C, GUPTA S, ZHANG Z J. Note on Self ̄restraint as an Online Entry ̄deterrence Strategy [J]. Management Science, 2006, 52(11):1799-1809.
[12]YOO W S, LEE E. Internet Channel Entry: A Strategic Analysis of Mixed Channel Structures [J]. Marketing Science, 2011, 30(1): 29-41.
[13]CHIANG W K, CHHAJED D, HESS J D. Directing Marketing, Indirect Profits: A Strategic Analysis of Dual ̄channel Supply ̄chain Design [J]. Management Science, 2003, 49(1): 1-20.
[14]ZHANG X. Retailers’ Multichannel and Price Advertising Strategies [J]. Marketing Science, 2009,28(6): 1080-1094.
[15]KOLLMANN T, HASEL M. Cross Channel Cooperation: On the Collaborative Integration of Online and Offline Business Models of E ̄entrepreneurs and Traditional SMEs [J]. International of Journal Entrepreneurship and Small Business, 2008, 6(2): 212-229.
[16]ZHANG J, FARIS P W, IRVIN J W, et al. Crafting Integrated Multichannel Retailing Strategies [J]. Journal of Interactive Marketing, 2010, 24(2): 168-180.
[17]DINNER I M, HEERDE H J, NESLIN S A. Drving Online and Offline Sales: the Cross ̄channel Effects of Traditional, Online Display, and Paid Search Advertising [J]. Journal of Marketing Research, 2014, 51(5): 527-545.
[18]PAUWELS K, NESLIN S A. Building with Bricks and Mortar: the Revenue Impact of Opening Physical Stores ;in a Multichannelenvironment [J]. Journal of Retailing, 2015, 91(2): 182-197.
[19]CAO L, LI L. The Impact of Cross ̄channel Integration on Retailers’ Sales Growth [J]. Journal of Retailing, 2015, 91(2): 198-216.
[20]FRUCHTER G E, TAPIERO C S. Dynamic Online and Offline Channel Pricing for Heterogeneous Customers in Virtual Acceptance [J]. International Game Theory Review, 2005, 7(2): 137-150.
[21]JORGENSEN S, TABOUBI S, ZACCOUR G. Cooperation Advertising in a Marketing Channel [J]. Journal of Optimization Theory and Applications, 2001, 110(1): 145-158.
[22]KARRAY S, MARTIN ̄HERRAN G. A Dynamic Model for Adverting and Pricing Competition Between National and Store Brands [J]. European Journal of Operational Research, 2009, 193(2): 451-467.
[23]陈东彦, 于浍, 侯玲. 考虑延时效应的供应链动态合作广告策略研究[J]. 管理科学学报, 2017(9):30-40.
[24]ZHOU J, WANG Y, YAN X. Joint Pricing and Purchase Decisions for the Dual ̄Channel Newsvendor Model with Partial Information [J]. Journal of Applied Mathematics, 2014:1-12.
[25]MARTIN ̄HERRAN G, TABOUBI S. Price Coordination in Distribution Channels: A Dynamic Perspective [J]. European Journal of Operational Research, 2015, 240: 401-414.
[26]LIANG T, HUANG J. An Empirical Study on Consumer Acceptance of Products in Electronic Markets: A Transaction Cost Model [J]. Decision Support Systems, 1998, 24:29-43.
[27]KACEN J J, HESS J D, CHIANG W K. Bricks or Clicks? Consumer Attitudes Toward Traditional Stores and Online Stores [J]. Global Economics and Management Review, 2013, 18(1): 12-21.
[28]YUE X, LIU J. Demand Forecast Sharing in a Dual ̄channel Supply Chain [J]. European Journal of Operational Research, 2006,174 (1): 646-667.
[29]牛志勇, 黄沛, 王军. 公平偏好下多渠道零售商线上线下同价策略选择分析[J].中国管理科学, 2017(3): 121-129.
[30]DIXIT A K. A Model of Duopoly Suggesting a Theory of Entry Barriers [J]. Bell Journal of Economics, 1979, 10(1): 20-32.
[31]SINGH N, VIVES X. Price and Quantity Competition in a Differentiated Duopoly [J]. The RAND Journal of Economics, 1984, 15(4): 546-554.
[32]RUBEL O, ZACCOUR G. A Differential Game of a Dual Distribution Channel [M]. Berlin: Birkhuser Boston,2007:547-568.
[33]PONTRYAGIN L S, BOLTYANSKII V G, GAMKRELIDZE R V, et al. The Mathematical Theory of Optimal Processes [M]. New York: Interscience Publishers, 1962.
(責任编辑:杨 洋)

