例谈思考题教学促进学生思维能力的发展

仇飞舟

【摘要】教育的主要任务不是积累知识，而是发展学生思维。思考题是学生思维训练的重要课程资源，在平时的课堂教学中，我们要让思考题教学充分发挥其优势，培养学生灵活运用所学知识解决问题，从而发展学生的思维能力。

【关键词】求异思維 创新思维 立体思维

教育家裴斯泰洛齐认为：教育的主要任务不是积累知识，而是发展思维。《义务教育数学课程标准（2011年版）》强调学生是学习的主体，要培养学生运用所学知识灵活解决生活中的实际问题，发展学生的思维能力。在以往的课堂上教师会说：和他方法一样的举手。现在的课堂上教师会这样问：还有不一样的想法吗？教师们已非常重视培养学生从不同的角度，用不同的方式去解决问题，在课堂上要激活学生的思维，鼓励学生标新立异，只有这样，学生才会活学活用。

2014年新版的苏教版小学数学教材中新增了一些思考题。笔者以为，思考题是学生思维训练的重要课程资源，在平时的课堂教学中，我们要让思考题教学充分发挥其优势，促进学生思维能力的发展。

一、精选教学内容，培养学生的求异思维

学生的思维能力只有在思维的活跃状态下才能得到有效的发展。在教学过程中。教师要根据思考题的特点，鼓励学生敢于求“异”，说出自己不一样的见解，发展他们的求异思维，进而养成独立思考问题、解决问题的能力。

例如，苏教版六年级上册第25页有这样一道思考题：

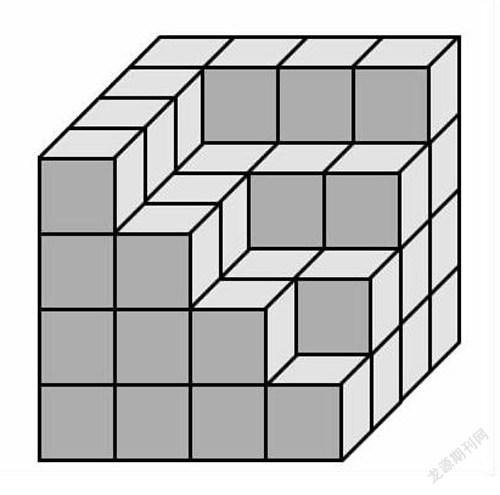
下图中一共有多少个正方体。你是怎样数的？与同学交流。

让学生自主思考，充分交流，个别汇报，精彩非凡。

生1：可以从上往下一层一层地数，先数第一层有7个：接着看第二层，第二层是5个吗？原来还有7个被第一层给遮挡住了，那么第二层应该是7+5 =12（个）;第三层也有部分被第二层给遮挡了，我们看到的就是第三层比第二层多的3个小正方体，应该是7+5+3=15（个）;同样的道理，第四层就比第三层多1个，即7+5+3+1=16（个）;把四个数加起来，小正方体的总个数为：7+12+15+16=50（个）。

生2：先把物体补成棱长为4个单位的正方体，现在小正方体的总个数是4x4x4=64（个），再从下往上减去每一层缺少的小正方体个数，第三层缺少1个，第二层缺少4个，第一层缺少9个，那么小正方体的个数是：64-1-4-9=50（个）。

生3：找相同形状的由外向内，一层一层地数。最外面有7个这样的小正方体，它有4层，则7x4=28（个）;第二组有5个这样的小正方体，它有3层，则Sx3=15（个）;第三组有3个小正方体，它有2层，则3x2=6（个）;最后一组只有1小正方体。那么小正方体的个数总共是：28+15+6+1=50（个）。

3个学生的回答出乎教师的意料，他们思维缜密，方法简单易懂，让一道原本抽象的数正方体个数的问题变成了发展学生求异思维的很好的素材。多么奇妙、缜密的思路啊，在解决问题的过程中，他们的思考互相碰撞，迸发了思维的火花。

二、巧用数形结合，培养学生的创造思维

在解决数学较复杂的实际问题时，最好的方法就是化抽象为具体，让其变得形象直观。如可以引导学生画线段图或集合图等，用数形结合的思想方法来解决问题。

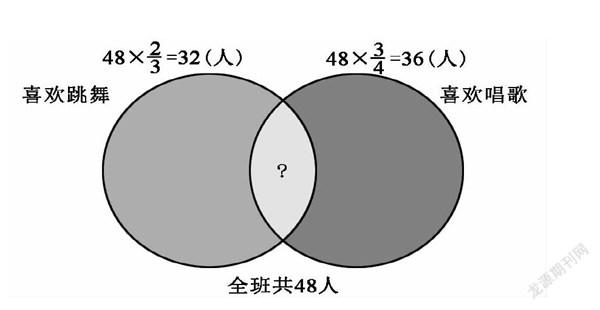
例如，六年级上册第83页有这样一道思考题：六年级一班有48人，其中2/3喜欢跳舞，3/4喜欢唱歌，没有人既不喜欢跳舞又不喜欢唱歌。既喜欢跳舞又喜欢唱歌的有多少人？

学生遇到这样的题目，一筹莫展，笔者以为，可以引导学生用画集合图的方法表示题中的各部分数量，先算出喜欢唱歌和喜欢跳舞的共有多少人：48×2/3=32（人）;48×3/4=36（人）;32+36=68（人）

根据集合图思考：为什么喜欢唱歌和喜欢跳舞的总人数比全班的总人数还要多68-48=20（人）呢？

让学生结合图来想一想！原来多出来的“20人”就是既喜欢跳舞又喜欢唱歌的人数，这部分被重复计算了一次。

列综合算式计算：48×2/3+48x3/4-48=20（人）或48×（2/3+3/4-1）=20（人）。

还可以根据集合图，分别让学生算出喜欢唱歌和喜欢跳舞的人数.48×2/3=32（人）;48x3/4=36（人）;再用48-32=16（人）。结合图来想一想：“16人”是图中哪一部分呢？对，这个16人就是只喜欢唱歌的人。那么既喜欢跳舞又喜欢唱歌的人数是：36-16=20（人）。

同理，也可以用48-36=12（人）算出只喜欢跳舞的人;再用32-12=20（人）算出既喜欢跳舞又喜欢唱歌的人数。

综合算式分别是：48x3/4-（48-48×2/3）=20（人）

或：48×2/3-（48-48×3/4）=20（人）

有了集合图的辅助，学生的脑洞大开，深刻地理解了题意，找到解决问题的突破口，思维顿时活跃起来，一个又一个创新的方法喷涌而出，思维得到充分的训练，非常轻松地解决了看似复杂的思考题，获得了成功的体验。

三、换个角度思考，培养学生的立体思维

一些数学问题，如果采用常规解法比较繁杂，或者“此路不通”，不妨换个角度思考，努力寻找解决问题的最佳路径，有时就因为转换了思维角度，“柳暗花明又一村”，使你走向了顺利解决问题的“康庄大道”。

例如，苏教版六年级上册第106页有这样一道思考题：学校田径队女生人数原来占1/3，后来有6名女生加入，这样女生人数就占田径队总人数的4/9。现在田径队有女生多少人？

解决这样较复杂的分数实际问题，通常我们习惯把整体，即学校田径队总人数看作单位“1”，可这题中的单位“1”的量发生了变化，乍一看无从下笔，怎样才能让学生走出思维误区，笔者以为只有从单位“1”上做文章。

思路1：寻找不变量，统一份数

男生人数是不变量

原来女生：总数=1：3→女生：男生=1：2=5：10

现在女生：总数=4：9→女生：男生=4：5=8：10

男生的人數是一样的，原来的男生是2份，现在男生是5份，我们要把人数变成一样的份数，就要找到2和5的公倍数，为了计算更加简单，我们找2和5的最小公倍数。根据比的基本性质我们把1：2变成5：10.把4：5变成8：10。引导学生仔细观察，原来的女生是5份，现在的女生是8份，为什么会变多的呢？哦，原来是因为新增了6名女生，多出来的3份就是6人。

8-5=3份→6人

6÷3=2（人），每份有2人。

8x2=16（人），现在女生有16人。

写成综合算式是6÷（8-5）x8

让学生明白抓不变量解决问题的解题思路：找不变量的最小公倍数，将不变量统一份数。

思路2：转化单位“1”，用分率

原来的总人数和变化后的总人数并不相同，所以我们要先统一单位“1”。因为男生的人数始终没有变，所以把男生人数看作单位“1”。

原来女生：男生：1：2→女生人数是男生的1/2

现在女生：男生=4：5→女生人数是男生的4/5

这两个分率的单位“1”都是男生，那为什么现在女生占男生的分率变大的呢？也是因为又来了6名女生。所以我们可以知道，由此找到6所对应的分率。

根据对应数量÷对应分率=单位“1”

求出来的是单位“1”的量，也就是男生的人数，再根据男生的人数求出女生的人数。让学生明白：找准对应量和对应分率，做到量率对应。我们可以根据对应数量÷对应分率求出单位“1”。不管量率对应还是分率加减，关键都在单位“1”上，量率对应是为了求单位“1”，而分率加减得单位“1”统一才能加减，所以在解题时一定先要搞清楚单位“1”。

思路3：方程思想

（直接设未知数：男生为x）由于男生人数没有变化，所以可以设男生人数为x人，那么现在女生人数就是（4/5）x，原来女生人数就是（1/2）x。根据等量关系：现在女生的人数一原来女生的人数=6.

（4/5）x-（1/2）x=6

列出方程，解方程得x=20，求得男生的人数。

提醒学生：不要忘记再根据男生的人数求出女生的人数！

此时，学生的思维顿时活跃了起来，还有学生想到了其他列方程的方法。

设田径队原来的人数为x，那么原来男生人数为2/3x，现在男生人数为5/9x，根据男生的人数不变，列出方程。

（2/3）x=5/9（x+6）

北师大教授顾明远先生说：“比知识更重要的是思维能力的培养和看问题的视角。”笔者以为，教育的本质从某种意义上来讲就是培养学生的思维，促进学生思维能力的发展。在平时的思考题教学中，我们应适时把握契机，透过现象看本质，引导学生对数学知识有更深刻的理解，从而促进学生思维能力的不断发展。

期待教师们每天都能改变一点点，一点点地改变……小