稚学课堂中拓展教学的价值
周孝丽



【摘要】为了丰富稚学课堂教学内容,激发学生学习数学的积极性和主动性,在实际教学过程中,教师应合理巧妙地选择拓展课内容,充分挖掘与教学内容相关的知识进行拓展教学,以促进学生对教学内容的理解和思考,培养学生的创新意识和发现并解决问题的能力,进而提高学生的数学思维能力。
【关键词】稚学课堂;数学思维;思维能力
稚学课堂中的拓展教学就是对小学数学教材进行扩充、延伸的课堂教学,通过创设问题情境,提供活动空间,让学生在动手操作、实践探究等活动中发现知识,感悟数学思想与方法,提高数学素养。稚学课堂的拓展课可以是对教材中某一概念进行追根溯源的探究,可以是对某一重点或难点知识的深入挖掘、开发,可以是对某一数学思想与方法的渗透、提炼,也可以是与其他学科知识的整合,等等。相对于数学基础课程,稚学课堂的拓展课在内容选取上有了更大的空间,因此更有利于培养学生的数学能力,发散学生的数学思维。本文以《长方形和正方形的面积》一课的拓展为例进行阐述。
一、稚学让认知更全面
1.稚学课堂源于生活
(1)从身边熟悉的事情引出新知
把现实生活中的情境融入稚学课堂,让学生在这种情境中尝试解决问题,会让学生有一种亲近感,同时也能使其快速接受预设的教学内容。
师:(播放视频)这是《最强大脑》中一次魔方比赛的规则,你们玩过魔方吗?我们学校每年的艺术节也都有魔方达人的比赛。刚刚视频中两次说到“三阶复原”,你们知道“三阶”是什么意思吗?(魔方的每个面都有3×3个小正方形,板书图形,见图1)。
师:如果是一个2阶魔方,那它每个面又是怎样的?
师:不管是2阶还是3阶魔方,它们每个面都是由这样的小正方形拼成的。
师:要知道图中分别有几个小正方形,你可以怎样算(板书:?×?)
教师从一段视频展开教学,激发了学生的学习兴趣,然后将教学焦点聚集在视频中出现的魔方上,又紧紧联系学生比较熟悉的比赛,引导学生观察魔方每个面上小正方形的排列规律,从而为后面出示的数列埋下伏笔。
(2)从生活中找到数学原型
《义务教育数学课程标准(2011年版)》指出:“数学教学要紧密联系学生的生活实际,从学生的生活经验和已有知识出发,创设生动有趣的情境。”小学生的智力还处于发展阶段,思维方式比较单一,因此,生动有趣的问题情境不仅能激发学生的学习兴趣,还有利于渗透数学思想,培养学生的数学思维能力。
师:如图2所示,这条曲线就是斐波那契螺旋线,这样的图案在我们身边随处可见:生存亿万年的鹦鹉螺(见图3)、盛开的向日葵(见图4)、人的耳朵(见图5)。这条曲线还颇得一些设计大师的青睐,这个图标(见图6)大家肯定都认识,它就是苹果公司的logo,设计师在每个正方形内添加圆,形成斐波那契直径圆,并以此创新设计出了这个logo。這种曲线最大的特点就是它的完美,所有的比例都显得恰到好处,让人看了身心舒畅。
通过欣赏生活中随处可见的曲线,学生恍然大悟,原来数学跟生活竟然有这么多的联系,这种教学模式激发了学生发现数学美的热情,充实了稚学课堂的内涵。
2.稚学课堂服务于生活
学以致用,充分体现了学与用之间的关系。稚学课堂不仅要让学生学会知识,而且要培养学生的应用意识与应用能力。在教学中,教师引导学生把所学的新知识运用到现实生活中,可以培养学生解决实际问题的能力,增强学生对数学价值的认识,激发学生学习数学的热情。
师:五一假期,我的闺蜜送了我一块桌布,等我打开一看傻眼了,你们猜猜看,为什么老师傻眼了?
生1:大小不一样。
生2:形状不同。
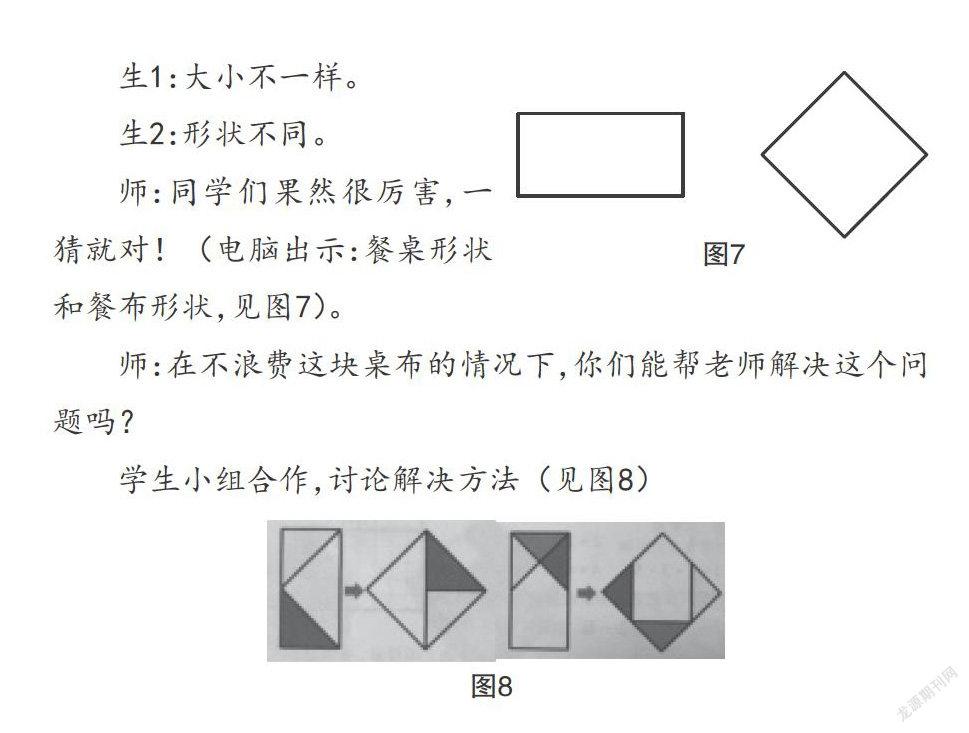
师:同学们果然很厉害,一猜就对!(电脑出示:餐桌形状和餐布形状,见图7)。
师:在不浪费这块桌布的情况下,你们能帮老师解决这个问题吗?
学生小组合作,讨论解决方法(见图8)
师归纳小结:同学们刚刚通过画图想到了不同的解决方法,不同的拼接还形成了不同的优美图案,真是棒极了!不管是哪一种拼接,其实你们都是巧妙地利用了正方形的对角线,在不改变面积的前提下,把长方形转化成了正方形。
学生在将知识应用于实践的过程中,也培养了自身的创新意识和创造能力。由此可见,稚学课堂给学生带来了满足感和荣耀感。
二、稚学让思考更深刻
1.数形结合,巧妙搭配
数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,从而“以形助数”或“以数解形”,即通过抽象思维与形象思维的结合,使复杂问题简单化、抽象问题具体化,从而实现优化解题途径的目的。
师:出示一组数列1、1、2、3、5、8、13…,它有规律吗?
生:1+1=2,1+2=3,2+3=5…
师:那这一组数列会跟正方形有关吗?
学生疑惑。
师:给点提示大家,出示1、1、2、3,你发现了什么?把你们的发现在方格纸上画下去(如图9)。
师:谁来说说为什么这样画?原来这一组数列中的每一个数都是这些正方形的边长。
对于抽象的数学概念,教师可以借助图形使之形象化、直观化,把抽象的数学语言转化为直观的图形,以便学生对其进行分析和理解,这样的教学手段可以称之为“以形助数”。在这里,教师通过画图把数列和图形之间的关系建立起来,从而让数学学习变得更简单,同时也加深了学生对正方形的认识。
2.形形结合,巧构联系
在解决问题时,根据需要,教师还可以引导学生从一个图形想到另一个图形,从一种图形创造出另一种图形。
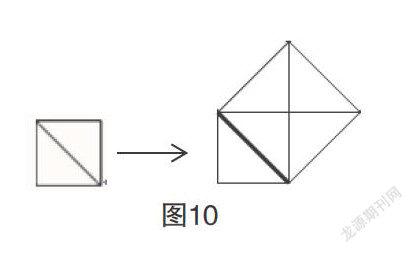
师:在正方形里面画一条线段(对角线),如图10所示,你觉得正方形的面积跟它有关系吗?你能用画图的方法来说明你的猜想吗?试试看,小组合作研究。
生1:现在构造的大正方形的边长是小正方形的对角线,大正方形的面积是小正方形面积的两倍;
生2:求原来正方形的面积,只要用对角线乘对角线的积再除以2就行了。
三、稚学让思维更开放
有机渗透跟课堂教学相关的数学文化知识,不仅能够彰显数学文化的价值,还能充分发挥稚学课堂的育人力量。例如,在教学《正方形的秘密》这一课时,除了相关的正方形知识,教师还引入了两种数学思维方式,以激发学生参与学习的兴趣,体现稚学课堂奇思妙想之精彩。
1.兔子数列
1、1、2、3、5、8、13…这一组数列,是有名的斐波那契数列(见图11),它是意大利数学家列昂纳多·斐波那契以兔子繁殖为例而引入的,故又称为“兔子数列”。教师通过介绍让学生明白这一数列的起源与发现,了解数学知识的形成过程,充分体现了稚学课堂尊重学生的特性。
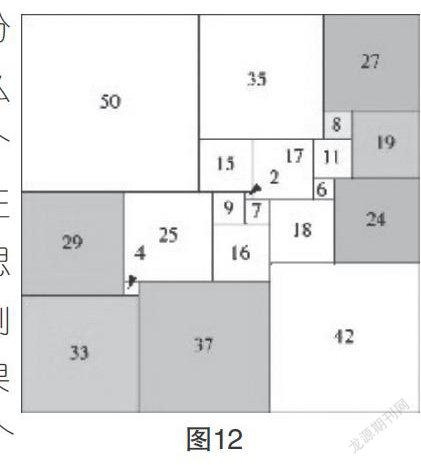
2.完美正方形
正方形或某些长方形可以分割成大小相同的小正方形,那么它能否分割成大小不同的若干个小正方形呢?这就是有名的“正方分割问题”。数学家们一直在思考,能不能把一个大正方形分割成若干个不同的小正方形?如果存在这样的大正方形,那么这个大正方形就叫作完美正方形。1978年,荷兰数学家杜伊维斯廷借助计算机技术,成功地构造出边长是112的一个21阶完美正方形(见图12),同时还证明了这是一个阶数最低的完美正方形。
在稚学课堂中,合理有效进行拓展教学是面向全体学生全面发展的同时,兼顾满足学生未来发展的需求。适时适度、别开生面的拓展数学知识,形成有层次的数学教学,是课程改革对每位数学教师提出的新要求,也是课程改革向纵深处发展强有力的推手。
【参考文献】
陈加仓.小学数学拓展课——教什么,怎么教[M].北京:中国人民大学出版社,2017.

