HPM视角下的平面向量概念教学

黄蓓　周天婷

摘要：尝试在《平面向量》一课教学中融入数学史，有利于初中生更好地理解向量这个全新的概念。其中，创设物理情境，引导学生抽象出向量概念的本质，设计向量概念的名称与符号，属于重构式融入数学史;播放有关向量由来及向量符号演变的视频，属于附加式融入数学史;最后呈现小船问题，引出海伦采用的平行四边形定则，为下节课做铺垫，则属于复制式融入数学史。课后学生反馈表明，这样的教学取得了较好的效果。

关键词：HPM 平面向量 概念教学

向量在中学数学中有着重要的地位，它既是代数的研究对象，也具有重要的几何性质，是沟通代数、几何与三角的桥梁。张奠宙先生在《话说向量》一文中提到：“向量在中学数学由20世纪80年代的配角地位逐渐变成21世纪更加重要的主角地位，这是因为向量能够精中求简，以简驭繁。”

在沪教版初中数学教材中，“平面向量”是八年级第二学期第二十二章《四边形》第四节第二课时的内容。对于初中生来说，平面向量是一个全新的概念，与以往所学的数量、长度不同，向量既有长度，又有方向;教材内容也比较抽象，不好把握。

为了让学生较好地理解这个全新的概念，教材本章前三节引导学生学习所有特殊的平行四边形和梯形，而本节第一课时引导学生学习基于平移运动定义的有向线段概念及其画法。通过一个点往某个方向平移一段距离得到一条有向线段，然后利用有长度、有方向的线段引出向量，符合学生原有的认知水平，学生容易接受和理解。

不过，如何让学生更好地理解这个全新的概念呢？我们认为，还要帮助学生解决如下问题：（1）为什么这个既有方向又有大小的量叫作“向量”？这个名称是如何来的？有没有其他的名称？（2）向量的符号表示有怎样的历史？历史上有多少种向量表示方法？（3）学习向量的意义是什么？我们为什么要学习向量？其中，最后一个问题是概念教学中最重要的问题：让学生了解所学概念的实际意义，才能让学生产生学习的兴趣。为此，我们尝试在教学中融入数学史：任何一个数学概念都可以从源远流长的历史中找到其发生、发展的背景与脉络。

一、历史材料梳理

（一）19世纪中叶以前的向量概念

在历史上，物理中的速度与力的平行四边形定则是向量理论的一个重要起源，由此发展起来的向量理论直到19世纪上半叶都主要与物理应用紧密结合在一起的。

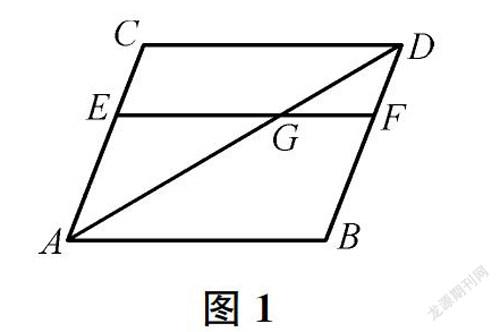
古希腊时期，速度作为既有大小又有方向的量，被认为是一个向量。约公元前350年，古希腊著名学者亚里士多德在其著作中有这样一段描述：“一个物体以一定比率速度运动时（朝着两条路径以定比率速度运动），该物体必定沿着一条直线运动，此直线是以定比率速度为邻边构成的平行四边形的对角线。”同一时代，亚历山大的海伦（Heron，1世纪）证明了速度的平行四边形定则：如图1，动点G沿着线段AB从点A向点B匀速运动，同时线段AB沿着一定的方向匀速平行于自己运动（即平移），假设点G到达点B处时，线段AB到达线段CD的位置，EF是AB运动过程中任意时刻所处的位置。由此易得AE∶AC=EG∶EF，进一步可知AE∶EG=AC∶EF=AC∶CD，所以AG与AD共线，因此点G的运动轨迹是对角线AD。

之后，牛顿基于亚里士多德的速度平行四边形定则，进一步描述了力改变物体运动状态规律的特征。他是最先使用有向线段表示力的科学家。牛顿和亚里士多德虽然已经运用了向量的一些运算或性质，但是没有将其抽象为向量。第一个给出“向量”这个名词的人是英國数学家哈密顿（W.R.Hamilton，1805—1865）。他在1853年发表的《四元数讲座》中介绍了他的向量思想，对这一数学方法进行了系统的说明。

（二）19世纪中叶至20世纪中叶英美几何与代数教科书中的向量概念

这一时期，英美几何与代数教科书中的向量概念大致可以分为“基于物理量的定义”“基于有向线段的定义”“基于复数的定义”和“基于平移运动的定义”四类。

将力、位移、速度等物理情境下的有向量描述为“基于物理量的定义”，是出现次数最多的向量定义。这类定义最初的思想源于亚里士多德，即物理学科中的矢量。物理情境下，向量有三个关键要素：大小、方向、位置。以力为例，力的刻画必须有作用点、大小和方向。

考虑线段两个端点的有序性是有向线段产生的原因之一。有向线段是出现次数第二多的向量定义。例如，温特沃斯（G.A.Wentworth，1835—1906）定义向量为“有固定长度的有向线段”。莫纳汉（F.D.Murnaghan，1893—？）认为：“要接受向量的概念，必须先弄清有向线段的问题。”柯芬（J.G.Coffin，1877—？）等对向量的定义是：“向量是起点与终点相异的有向线段，因此向量有大小和方向，任何能用有向线段表示的量都是向量。”

第一次提出用向量表示平移的是哈密顿——英文“vector”（矢量、向量）一词源自拉丁文“vehere”一词，隐含着将某物从此处带到彼处的意思。之后出现的基于平移的向量概念，或多或少继承了哈密顿的定义。例如，泰特（P.G.Tait，1831—1901）将向量定义为“将一点运载到另一点的工具，因此向量可表示空间中特定的平移”。

基于复数的定义对于初中生来说理解困难，在此不予细说。

（三）向量符号及中文翻译（名称）的演变

向量的符号在历史上是丰富多彩的，经历了漫长时间的争议，才形成了统一的现代符号系统。在早期的英美几何与代数教科书中，不同的数学家用于表示向量的符号也不尽相同。莫纳汉认为，一条直线上有任意两个点A、B，当考虑顺序时，谁被第一个提及就非常重要了：若点A被第一个提及，则说明点A是起点，点B是终点，记作A→B;反之，记作B→A。向量也可以用符号V（A→B）来表示。弗雷姆（Frame，1907—？）则用类似于↑（AB）的符号来表示向量。

1806年，阿尔冈（R.Argand，1768—1822）以AB表示一个有向线段或向量。1872年，莫比乌斯（A.F.Mobius，1790—1868）以AB表示起点为A、终点为B的向量。这种用法被数学家广泛接受。另外，哈密顿、吉布斯（J.W.Gibbs，1839—1903）等人则以小写希腊字母表示向量。1912年，兰格文用a→表示向量。此后，字母上加箭头表示向量的方法逐渐流行，尤其在手写稿中。为了方便印刷，人们又用粗体小写字母a、b等表示向量。这两种表示方法一直沿用至今。

随着西方物理学和数学的引进，向量概念在中国得以传播和发展，其中文名称经历了比较长时间的演变。向量概念刚传入中国时，根据含义，被翻译成“动量”，意为定方向上的定距离移动。后来，在物理学中被称为“有向量”，在数学中被称为“有向数”。此后，区分还是统一物理学与数学中的向量名称一直广受争议，原因在于，一部分人认为“向量”和“矢量”没有本质的区别，而另一部分人则认为“矢量”与“向量”有着本质的区别。1985年，数学名词审定委员会成立后，统一规定：物理中称“矢量”，数学中称“向量”。这样的名称一直延用至今。

二、教学设计与实施

基于对教材编写及历史素材的分析，我们设计和实施的本节课教学过程如下：

（一）创设物理情境，抽象概念本质

教材利用小明问路的情境，结合第一课时学习的有向线段画出线路图，从而引出向量概念。我们认为，这样容易使学生产生负迁移，因为向量是自由的，而有向线段是固定的。所以，我们选择了历史素材中出现最多的“基于物理量的定义”，利用学生熟悉的物理量——速度，引导学生抽象出向量的基本特征——既有大小又有方向，让学生了解早期的向量概念来自物理学，培养数学抽象素养。此外，我们还通过追问，使学生了解到这种量在实际应用中普遍存在。

师请大家先来看这样一个问题：小船从点A出发，速度是4米/秒，请问2秒后它开到了哪里？

生离点A 8米的地方。

师具体的位置移动到哪里了呢？

生不知道。

师为什么会不知道呢？

生没有给出方向。

师所以说，我们虽然知道位置移动了8米，但是并不知道具体位置到了哪里。再来看这样一个问题：条件变一下，现在小船还是从点A出发，向正北方向行驶，请问2秒后它开到了哪里？

生还是不知道。

师为什么？

生因为虽然告诉了我们行驶的时间，但是没有告诉我们速度的大小。

师刚才两个问题，第一个问题是不知道速度的方向，所以我们不知道这个小船到底开到了哪里;第二个问题是不知道速度的大小，所以我们也没办法确切地知道小船开到了哪里。所以，我们需要重新审视一下“速度”这个量：它到底是一个怎样的量？

生是一个既有大小又有方向的量。

师同学们在平时的学习过程中有没有接触过这样的量？不一定是数学学科的，也可以是其他学科的。

生地图上面的路线图，需要既有方向又有大小。

生力。

（二）开放讨论，设计概念名称与符号

让学生给向量概念取名和设计符号，可以呈现学生学习的“历史相似性”，从而让学生加深对向量概念的理解，并感受数学是不断发展的，建立动态的数学观。通过观看视频让学生了解向量的由来以及向量符号的演变，可以让学生认识学习向量的必要性，体会向量历史的演进。在此基础上，教学向量大小（长度）的名称和符号，突出概念的本质，顺应学习的自然。

师所以像力、速度这样的量是既有大小又有方向的，那么同学们能不能给这样的量取个名字？你想给它取个什么样的名字呢？

生指示量：有方向的指明。

生數向：数代表大小，向代表方向。

生向长：向代表方向，长代表长度。

生方位值：方位代表方向，值代表大小。

师在数学中，我们把既有大小又有方向的量称为向量。由于我们现在研究的是平面中的向量，因此我们就叫它平面向量。（稍停）定义是什么？

生既有大小又有方向的量叫作向量。

师图形语言是什么？

生有向线段。

师不可能总是在表示向量时画有向线段，所以我们需要用一个符号来表示向量，那么我们可以用怎样的符号语言来表示向量呢？同学们也先自行设计一下，看看你们都有什么创意。

生先把这个线段的长度用数字写出来，再在数字上面写上箭头表示方向。

师那么数字代表什么？

生数字代表大小，箭头代表方向。

师那么箭头方向往哪里画呢？

生根据题目，题目中方向往哪里，就把方向往哪里画。

生我写的是A→B，从起点A到终点B。

师同学们都设计了向量的符号表示。下面，我想请同学们看一段视频，看看向量从古至今的发展及其符号的演变。

（教师播放有关向量由来以及向量符号演变的视频。学生观看。）

师我们可以发现，刚才一位同学设计的向量符号就是视频中提到的莫纳汉发明的符号。如果这位同学生活在那个年代的话，他就能成为莫纳汉了！（稍停）我们刚才也看到了，在古希腊，亚里士多德解决力学问题时就已经用到了向量的性质，但是那时并没有抽象出向量概念;而现在，我们的数学家已经把向量发展成为一门工具学科，用它来解决实际问题和物理学问题。看来，学科之间是相通的，而且今朝更胜于往昔。（稍停）向量的方向可以用有向线段和符号等来表示，那向量的大小也需要表示出来。首先，我们把向量的大小称为向量的模。其次，向量的模也可以用一个符号来表示，这个符号我们曾经学过，只不过那时候不叫模，而叫——

生绝对值。

师为什么会想到绝对值？

生绝对值是正的，而且可以表示长度。

师绝对值应该是非负数;而且绝对值可以表示线段的长度，就是相应点到原点的距离。所以，向量的模可以用向量外面加两竖来表示，如|AB|。

（三）运用新知，解决问题

我们设计了两道例题。例1既考查学生是否已经掌握前面所学的向量表示法，也为学生后面学习相等向量、相反向量、平行向量等概念提供背景。

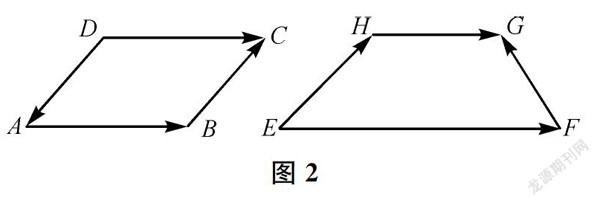
例1如图2，ABCD是平行四边形，EFGH是梯形，EF∥HG，图中的有向线段都表示向量，它们的起点和终点分别是所在四边形的顶点。

（1）用符号表示各个向量;

（2）每个四边形对边上的两个向量的方向是否相同或相反？它们的长度是否相等？

利用例1中的有向线段实例，引出相等向量、相反向量、平行向量的概念后，教师要特别注意帮助学生厘清概念之间的联系与区别，建立良好的知识结构;尤其是针对学生受直线平行与重合关系的负迁移影响，认为共线向量不是平行向量的想法进行纠正——

师平行向量只需要考虑方向，不需要考虑大小。那么，方向相同的两个向量能叫平行向量吗？

生可以。

师方向相反的两个向量能叫平行向量吗？

生可以。

师没错，只要位置上平行，就可以称为平行向量，方向相同或者相反都可以。那么，平行向量和相等向量、相反向量有什么关系？

生相等向量和相反向量都是特殊的平行向量。

师这句话对不对？

生我不同意，因为如果这两个向量共线的话，那么它们方向相同或者相反，就不是平行向量了。

师同学们，向量是自由的，你可以想象向量在保持大小和方向不变的情况下，在平面中自由地飞翔，那么，你觉得在一条直线上的两个向量可以说是平行向量吗？

生可以。

师没错。你可以把它们平移开，不就变成平行的位置关系了吗？

例2则引导学生体会向量是代数与几何的桥梁，运用向量的关系可以方便快捷地解决几何问题。

例2（1）在四边形ABCD中，AB=DC，则四边形ABCD为;

（2）在四边形ABCD中，AB=DC，|AB|=|BC|，则四边形ABCD为;

（3）在四边形ABCD中，AB∥DC，|AC|=|BD|，则四边形ABCD为;

（4）在四边形ABCD中，AB∥DC，|AD|=|BC|，则四边形ABCD为。

（四）反思小结，承上启下

课尾，教师引导学生对本节课学习的内容进行简要的反思总结：从知识层面上看，知道了向量的定义;从数学史的角度来看，了解到任何一个新的数学概念的产生都是数学家们前赴后继努力研究的结果;从应用层面上看，发现向量的运用是广泛的，不仅可以应用于物理学科，也可以应用于地理、生活等各个方面，还能使几何证明变得简洁且明朗;从数学思想的角度来看，体会到向量很好地体现了数形结合思想。

最后，教师介绍古希腊数学家海伦利用速度的平行四边形定则解决的小船速度问题，为下节课向量加法的学习做铺垫;并且，抓住向量概念的内涵，对学生进行人生教育——

师让我们再回到小船问题：如果小船以4米每秒的速度朝正北方向开，而水也以1米每秒的速度向正东方向流，请问最终小船的速度是怎样的呢？

生会偏。

师为什么会偏？偏到怎样的一个程度？偏了之后有多大？古希腊数学家海伦也曾经一直在思考这些问题，并最终证明了速度的平行四边形定则。而大家学习了下节课的内容，就能知道如何解决这些问题了。（稍停）最后送给大家一句话：人生就如同向量，你不仅要知道自己从哪里来，更要知道自己将要到哪里去，因此，方向很重要！

三、学生反馈

课后，我们对全班学生进行了问卷调查及个别访谈。

对于“你觉得向量有用吗？”，学生的回答有的指向“数形结合”，认为可以简化几何题的证明等;有的指向“其他学科”，认为物理、地理等学科都会用到向量;还有的指向“生活实际”，认为向量可以用于指路、具体表明物体的位置变化等场合。

对于“这节课你印象最深的是什么？为什么让你印象深刻？”，有半数左右的学生提到了数学史，认为向量的由来以及向量符号的演变十分有趣，而视频的方式十分形象直观;还有一些学生提到了自己创造向量的名称与符号，认为这让他们更深刻地理解了向量概念，并充分体会到数学是在数学家们的努力下不断发展的。可见，数学史的融入让部分学生建立了动态的数学观。

通过访谈我们还得知，一些学生对课堂最后提及的小船问题十分感兴趣，并做出了一些思考。谈及收获时，学生还提出了“人生就如向量，要找到方向，走得正、走得直”等观点。

四、教学反思

本节课创设物理情境，引导学生抽象出向量概念的本质，设计向量概念的名称与符号，属于重构式融入数学史，构建了“知识之谐”，并且营造了“探究之乐”，实现了“能力之助”;播放有关向量由来及向量符号演变的视频，属于附加式融入数学史，构建了“知识之谐”，并且展示了“文化之魅”，達成了“德育之效”;最后呈现小船问题，引出海伦采用的平行四边形定则，为下节课做铺垫，则属于复制式融入数学史。

*本文系本刊连载的汪晓勤教授团队开发的HPM案例之一。

参考文献：

[1] 张奠宙，袁震东.话说向量[J].数学教学，2007（9）.

[2] 阮伟强.平面向量教学后记[J].中学数学研究，2004（3）.

[3] Swetz，F.Learn from the Masters[M].Washington：Mathematical Association of America，1995.

[4] Heath，T.L.A History of Greek Mathematics[M].Oxford：Clarendon Press，1921.

[5] Wentworth，G.A.A Higher Algebra[M].Boston：Ginn & Company，1891.

[6] Murnaghan，F.D.Analytic Geometry[M].New York：Prentice-Hall，inc，1946.

[7] Coffin，J.G.Vector Analysis[M].New York：Stanhope Press，1911.

[8] Tait，P.G.An Elementary Treatiseon Quaternions[M].Oxford：Clarendon Press，1867.

[9] Sutherland，J.F.Solid Geometry[M].New York：McGraw-Hill Book Co，1948.

[10] 孙庆华.向量理论历史研究[D].西安：西北大学，2006.