探索“4+”互动课堂 提高数学学习力

江巧根

【摘要】为了深入推进课程改革，提高课堂的有效性，提升学生的学习力，我校提出了“4+”互动课堂教学模式。本文以《直线与圆的位置关系》一课的教学为例，围绕“4+”课堂模式，精心设计教学活动，在课堂上采取“互动”教学，培养学生的数学学习力，希望能够为数学教学的探究提供参考。

【关键词】初中数学;课堂教学;学习互动;方法探究

在不断地课程改革实践中，我校创设了“4+”互动课堂教学模式，实践证明这种教学模式可以提高课堂的有效性，提升学生的学习力。本文就一堂区级示范课（苏科版九年级上册《直线与圆的位置关系》）的课堂部分实录，谈如何运用“4+”互动课堂教学模式来培养学生的数学学习力。

一、预习自学

1. 解读

对于数学的预习，学生往往就是粗读教材提供的文本，对一些概念、公式或定理的文字部分进行圈点，然后模仿例题的解答过程完成书本上的相应练习题。在此过程中，学生缺乏耐心，也没有意识来质疑概念、公式以及定理的合理性等问题。这样的预习和自学仅仅使学生提前了解新知识而已，却不能提高其自主学习能力。因此我校主张在课堂上由老师指导学生进行预习自学，促使学生根据问题导向边预习边思考。

2.课堂实录

教师通过提问题，引导学生进行思考，完成预习自学。

师：先阅读书本第63至65页，后思考下列问题。

（1）直线与圆的位置关系有哪几种？

（2）用什么方法来判断直线与圆的位置关系？

（3）直线与圆的位置关系实质上是垂足（过圆心的垂线与直线的交点）和圆的位置关系，那么在直线上是否还有其他点可以来替代呢？ 若有，指出这个点的位置，若没有，请说明理由。

（4）如何想到用圆心到直线的距离与圆的半径大小比较来判断直线与圆的位置关系？

3.说明

本堂课预习自学中的四个问题具有丰富的层次性，前面两个问题在教材中通过阅读可以直接找到答案，属于浅层次问题;后面两个问题要求学生具有较高的思维能力，书本中没有提供现成答案，属于深层次问题，教师要在课堂教学中让学生思维动起来，切实引导他们自主学习，在主动探究中自觉领悟。

二、教学点拨

1.“+1”环节：新课引入，培养归纳概括能力

（1）解读：数学课堂的引入形式多样，有问题引入、情景引入，等等。课堂引入的目的不仅在于引起学生学习的兴趣，方便新知识导入的学习，更重要的是在于引入过程中能培养学生的自主学习能力。课堂实录如下。

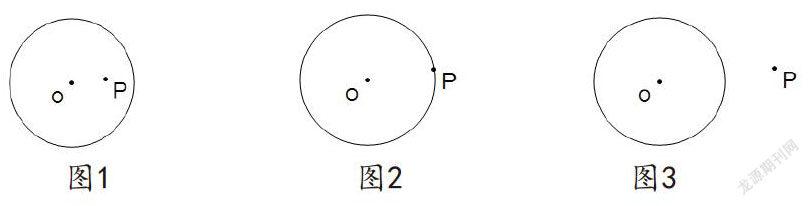
师：观察下面3个图（图1、图2、图3），点与圆的位置关系有哪几种？

生：圆内、圆上、圆外。

师：如何判断点与圆的位置关系？

生：比较点与圆心的距离与半径大小的关系。

（教师分别对每张图过点P作出与⊙O不同公共点的直线，并对每一张图就所画直线与圆的公共点个数进行归纳结论）

生1：图1的结论是：过圆内一点P可以作无数条直线，都与圆有两个公共点。

生2：图2的结论是：过点圆上一点P可以作无数条直线与圆有两个公共点，可以作一条直线与圆有一个公共点。

生3：图3的结论是：过点圆外一点P可以作无数条直线与圆有两个公共点，可以作两条直线与圆有一个公共点，无数条直线与圆没有公共点。

师：对这三张图中所作的所有直线，如何进行分类？

生：第一类是与圆有两个公共点的直线;第二类是与圆有唯一公共点的直线;第三类是与圆没有公共点的直线。

（2）说明：教师先复习点与圆的位置关系及判断方法，是为引出新课内容（直线与圆的位置关系）做好铺垫;教师画图，过与圆不同位置的点作出不同公共点的直线，是为了培养学生的作图能力和探究能力;根据所做直线的规律进行两次归纳，是为了培养学生总结归纳的能力，引导学生对几何问题的直观思考逐步过渡到对抽象图形的数学思考。

2.“+2”环节：课堂答疑，培养探究能力

（1）解读：教师要充分研究教材，善于给学生参与数学活动的机会，培养学生的学习力。例如，在教学点拨中，笔者抓住了学生课堂自学中的疑问进行答疑，与学生一起探究为什么只有垂足一个点满足要求。课堂实录如下。

师：类比点与圆的位置关系判断方法，能否在要判断的已知直线上也能找到一点P，比较OP的长度与半径大小关系，从而来判断直线与圆的位置关系呢？

生：在直线上任取一点，试试看。

（教师打开几何画板，给出直线上任意一点P）

师：直线上任意一点，能否说明吗？谁愿意来试试？

（学生用鼠标把已知直线绕着点P旋转，直线出现与圆三种不同位置，结果OP长度纹丝未动）

师：任意一点不行，那么就需要在直线上找一个特殊的点，如何找呢？我们移动点P在直线上的位置，看哪一点能符合要求。

生：过点O作OP垂直已知直线，得垂足，这个垂足就是所要求的。

师：对，为什么这个垂足就可以呢？请你利用几何画板来演示一下。

……

（2）說明：“4+”互动课堂的三大核心节点之一是课堂质疑讨论。提高学生的数学学习力，不仅要让学生做到“知其然”，更要让学生做到“知其所以然”。

三、拓展延伸

1.解读

要想让不同基础的学生有不同收获，笔者这样进行“反馈练习2”的拓展延伸，课堂实录如下。

师：把练习中第2题，变形为如下问题：

在△ABC中，∠C=90°，BC=3， AC=4，以C为圆心与边AB有一个交点时，求⊙C半径取值范围.

生1：求得点C到AB的距离为2.4，当AB与圆相切时，即R=2.4时，有一个交点。

生2：前面同学的回答不全面，当半径大于3时，⊙C与线段也会有一个交点。

师：由于本题中问的是⊙C与边AB即线段AB的交点，所以不是相切就是有一个交点的情形。下面请同学利用几何画板来看看，随着圆的半径变大，圆与边AB交点的各种情形，并提出相应的问题。

生3：当⊙C与边AB有两个交点，⊙C半径取值范围是什么？

生4：当⊙C与边AB没有交点时，⊙C半径取值范围是什么？

2.说明

把“反馈练习2”中的条件“直线”改成“边”，题目就变成了一个圆心不动、半径变化的动态问题。在解答这个问题的过程中，教师既要兼顾到相切的问题，还要兼顾到⊙C过临界点A、B的情形，跟踪动态圆的变化全过程，这样就运用到了分类讨论、数形结合的数学思想。

教师要根据不同的教学内容，积极探索 “4+”互动课堂教学模式，优化教学设计，不断提高教学效率，从而提升学生的学习力，培养学生的数学素养。

【参考文献】

冯华，梦轩，肖化化， 彭凡 ，功勋.挑战数学学习力[M].昆明：云南教育出版社，2008.