用“智性学习”方式提升学生的数学核心素养

陈金飞

摘要：数学科学是一个不可分割的有机整体，它的生命力正是在于各个部分之间的联系。只有从知识的内在结构出发，将知识关联起来，使各个知识点在学生的大脑中连成线、织成网，形成“知其然更知其所以然”的状态，才能展现数学学习应有的深刻与灵动。“智性课堂”是发展学生数学核心素养的一种具体实践方式，它从创设适切的问题情境、整体把握数学课程、抓住数学本质展开教学、提供深入探究和思考的机会、捕捉数学教育中的核心价值五个方面来培养学生的数学核心思维，提升学生的数学核心素养。

关键词：智性学习;智性课堂;数学联系;数学核心素养

对于数学学科来说，数学学习到底应该用何种学习方式？“智性学习”的倡导者英国教育心理学家斯根普认为，最有效的数学学习应是注重“数学联系”的学习。德国著名数学家希尔伯特也认为，数学科学是一个不可分割的有机整体，它的生命力正是在于各个部分之间的联系，只有从知识的内在结构出发，将知识关联起来，使各个知识点在学生的大脑中连成线、织成网，形成“知其然更知其所以然”的状态，才能展现数学学习应有的深刻与灵动，这亦是“智性学习”的精髓所在。实际上，这种教学理念，跟时下最熱门的培养学生数学核心思维，提升数核心素养的要求，是相一致的。

作为发展学生数学核心素养的一种具体实践方式，在课堂教学中，与“智性学习”的方式所对应的“智性课堂”需要从五个方面来使学生实现“智性学习”。

数学核心素养导向下的“智性课堂”，要求教师要善于根据具体教学要求创设合适的情境，引导学生运用所学的知识和方法，开展自主探究和合作探究，使学生经历在其中，感悟数学的发生、发展过程以及数学的本质，从而主动解决相应的隋境任务，发展学生的数学核心素养。

例如，苏教版教材中“分数的认识”这一部分内容，是直接引导学生从“倍数关系”中去理解，这与“分数是在度量、分物时不能正好得到整数的结果而产生”的事实相违，与“小数的初步认识”教学也脱节。学生在初步认识分数时，不知道分数还可以表示具体的数量，到认识小数时，教材凭空出现了“1米的3/10是2/10米”，而学生不懂“1/10米”所表示的含义，这就会导致学生对十进分数和小数之间的联系很难理解。鉴于此，我创造了一个以物换物的情境：2条鱼换一块肉，那么一条鱼可以换多大的一块肉？学生发现用学过的整数已不能表示，就很自然地要去创造一个新的数来表达。在物物交换的调整中，我让学生领悟以下三个问题：新的数为什么偏偏叫“分数”？产生新的数为什么首先要“平均分”？为什么新的数偏偏叫“几分之几”？学生弄明白了这几点，也就抵达了知识的本质，提升了数学素养。

现行各版本的教材普遍采用了“分步实现，螺旋上升”的原则来编排教学内容，这既有利也有弊。一方面，适当的螺旋式结构，可以很好地满足不同发展阶段学生的课程需求，符合学生思维发展的阶段性与理解水平的阶段性的现实要求;但另一方面，客观上造成了教学中过分关注一个个分散、零碎的“知识点”，很少去关注知识之间的联系和发展。学生如果按照这种体系来进行学习，他们很难明白所学的知识点在整个单元、整册教材，乃至整个教材体系中的地位和作用，这将不利于学生知识的提取和能力的提升。郑毓信教授曾说：“数学教学不应求全，而应求联。”这显然是要求数学教师不但要关注知识点的教学，更应重视沟通知识点之间的内在联系。“智性学习”的课堂，要求教师必须高屋建瓴，整体、有序地把握教材体系，了解每个“知识点”在整个学习系统中所处的地位和作用，把每堂课的学习目标放在整个教学体系的视野中来设定，引导学生理清教材的知识层次，重视知识之间的联系和规律，主动建构知识体系，达到“既见树木，又见森林”的教学效果。

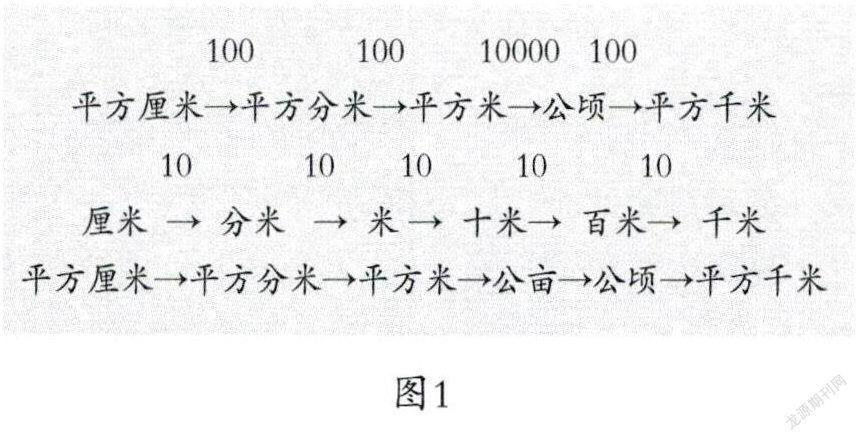
例如，在学习了面积单位“公顷和平方千米”之后，从建构系统的角度出发，教师可以引导学生整理出已经学过的5个面积单位的关系图，有了这样的整理，学生就可以比较轻松地实现面积单位之间的转换。在图1中，相邻两个面积单位之间的进率大多是100，唯有平方米和公顷之间。为什么完美的“规律”被打破了？不妨联系长度单位来理解。长度单位“厘米、分米、米”之间的进率是10，而千米与米之间的进率是1000，为什么会出现这种跳跃？原来，在米和千米之间省略了生活中很少用到的十米、百米这两个长度单位。如果将这两个长度单位编排进长度单位结构图中，学生就会容易理解长度单位之间的进率了。

由长度单位生发出对应的面积单位“平方厘米、平方分米、平方米、公亩、公顷、平方千米”，学生就会发现相邻的两个面积单位进率都是100。之所以出现“平方米”和“公顷”之间的进率是10000，原因是在平方米和公顷之间省略了一个面积单位“公亩”。如果将公亩编排进面积单位结构图中，学生就会更容易地理解面积单位之间的进率，也能很好的沟通长度单位与面积单位之间的联系，还易于生长出体积单位。这样，把长度单位、面积单位、体积单位构建成一个系统，会易于学生在系统中感受整体，在结构中实现建构。

教师把握数学知识的本质，是引导学生感知知识本质、提升学生数学核心素养的前提。抓住数学本质展开教学，可以帮助师生从纷杂的概念、法则、定理、公式中跳出来，站在更高的位置上培养学生的数学核心素养。

例如，在对面积概念的理解的教学中，很多教师组织学生摸黑板的面、摸书本的面，然后说有的大，有的小，这就是面积。即使就是生活中，大小也不是这个意思，比如说“你去看看那个房间的大小”，这里的大小显然是指房间的占地面积有多少平方米。

因此，教师完全可以从“量”的角度一所求面积中含有多少个单位面积去引导学生认识面积的意义。这样一来，就从更高的层面使学生达成了对知识的系统关注，将线段、面积、体积的度量统一为用数来表示“量”的大小，度量线段的长短需要确立单位“1”——长度单位。同样，度量面积的大小、体积的大小也就是单位“1”的确定。

积极思考是数学学习过程中最有价值的学习方式，听讲、动手是为了更好地帮助自己思考，交流是为了更好地启迪自己思考。从一定意义上来说，数学课就是学习如何思考，而学习路径就是在思考中学习思考，这就如同只有在下水游泳中才能学会游泳是一样的道理。

例如，在執教“圆的面积”一课时，我没有直接把计算公式灌输给学生，而是放手让学生在自主探究的基础上，自然地生成面积计算公式。课始，我先让学生回顾以前学过的平面图形面积计算公式的推导方法，他们发现这些图形都是由线段围成的，都是用转化的方法来推导出面积计算公式。而圆偏偏是个曲线图形，最直觉的方法便是“去曲成直”，学生很自然地把圆中曲的部分剪去或折去。这样的处理，问题显而易见，改变了原有图形的面积，所以“去曲成直”不可取。学生在心中很自然地会产生这样的想法：把圆剪开试试。有的学生把圆四等分后，发现能拼出一个近似平行四边形，只是底边太弯曲。怎样让底边变得“直”一些？一些学生受“折”的启发，认为如果继续分割，底边会变得更“直”。在多媒体演示不断细分的圆片后，他们发现得到的其中一份图形越来越趋近于一根线。这样，他们思维的障碍就获得了突破：圆之所以能转化成长方形，是因为由线拼成的图形，它的底边自然变“直”了。学生从“把弯曲的部分折（剪）掉就变成直的”，到“折着折着，弧度就有点变直了”，再到“分的份数越多，每块图形越来越像一根线，线的话是没有弧度了”，经历了一个“直观的极限过程”—在观察“有限分割”的基础上想象“无限分割”，根据拼成图形的变化趋势去想象它们的终极状态。从中学生领悟到：“将圆无限分割后拼成的才是真正的长方形。”从“圆的面积”的教学实践来看，只有为学生提供充分的数学探究和数学思考的机会，才能让学生感悟到“无限分割，化曲为直”的数学思想，从而提升学生的数学核心素养。

学习数学还需要了解数学的历史，了解数学的发展，了解数学在社会发展中的作用。透过知识的发生和发展可以使我们更好地理解数学知识的本质内涵，透过人类认识的提升发展可以使我们更好地把握学生认识提升的关键点。

例如，在“平均数”的教学中，通过梳理历史我发现，平均数概念的发展主要经历了三个阶段：用中等数据估计总数、用全部数据的平均数来减少误差、用全部数据的平均数作为总体水平的代表值。在梳理数学史的过程中，我受到启发：在教学设计时，应该把大数估计问题作为学生的认知起点，通过教学活动让学生再现这种方法，以培养他们对平均数的直觉能力。从学生的认知水平来看，学生对于理解平均数作为总体水平的代表值有困难，因此，我就把这个问题作为了本课的学习重点。我创设了“三年级二班参加套圈比赛”的情境，把学生分成两组，一组为男生，一组为女生，并进行了两次比较。第一次，双方人数相等，比总数;第二次，女生比男生多1人，引导学生寻找代表值。这时女生的三个数据相同，男生的两个数据不同，学生自然产生了匀平的想法，平均数意识在此时就萌发了。我再出示三年级三班的比赛情况，由于双方人数、每个选手的比赛成绩各不相同，这时学生自然就产生了用平均数作为代表值的想法。