高压开关中连杆机构的简便计算

陈贤会

摘 要：从操动机构动作到开关合分闸的中间环节的传动机构的设计是开关设计人员最重要的工作。开关此部分传动机构一般都是由一组或者几组四连杆机构组成，采用传统的公式去计算四连杆传动机的力矩是非常繁锁，而且也容易计算错误。本文采用不同的计算方式对几组高压真空断路器的四连杆机构的静态受力计算，总结出更加高效、简便的计算方式。

关键词：连杆机构;测量法;三角函数

一、引言

作为一名从事高压开关行业的设计人员，对开关机械部份的力矩计算的能力是必不可少的。从机构动作到开关合分闸的中间环节的传动机构的设计成了开关厂设计人员最重要的工作。而高压开关此部分传动机构一般都是由一组或者几组传动连杆机构组成，在静态受力分析一般都采用三角函数的方法去计算，在计算过程中太过繁锁很容易造成计算错误，以及计算效率不高。本文通过利用CAD绘图软件，结合新的计算方式，将更加高效、简便的方式来计算各连杆传动机构的受力情况。本文将采用不同的计算方式对连杆机构的力矩计算进行一个对比，来证明新的计算方式具有高效、简便的。

二、XGN74-12断路器柜传动组成概述

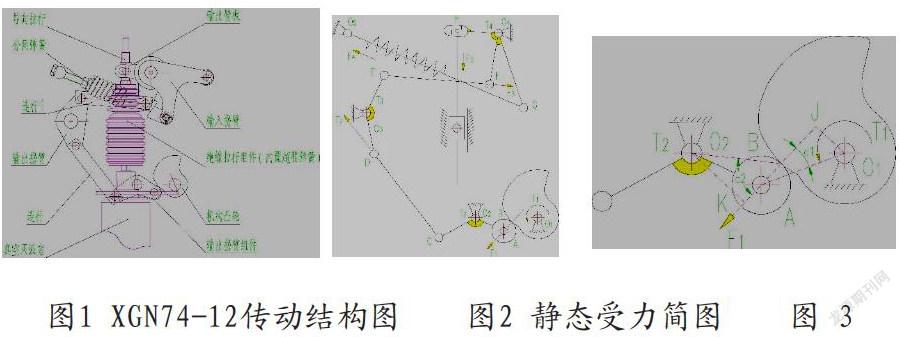
首先，我们要了解在设计XGN74-12断路器柜传动的过程中，从操作机构驱动开始到断路器完全合闸这一过程，都要有详细的传动过程计算。利用一组静态传动图，来证明两种计算方式对静态受力分析的一致性。本文将采用一组机构中的凸轮刚接触拐臂时的静态传动简图，利用两种不同的计算方式来进行对比。XGN74-12断路器操动机构到真空灭弧室的传动主要是由机构凸轮、输出拐臂组件、输出拐臂、输入拐臂、输出臂板等。具体结构见图1。

（一）机构凸轮刚接触传动拐臂时的传动简图及计算

图1中，紫色表示断路器电气本体部分，在机构后面，置于气箱内部。在图1中，为了方更计算，将作用在机构凸轮的力的合闸弹簧省略掉。在合闸弹簧过中后，在合闸弹簧的作用力下，机构凸轮逆时针旋转。将图1中，机构凸轮刚接触输出拐臂组件时的静态传动结构图采用传动简图方法表示。见图2。

在实际运行中，机构中的能量由机构中的合闸弹簧通过凸轮等传动件输出到机构输出拐臂，其整个运动过程较复杂，且整个运动过程受摩擦力等因素的影响，为了简化计算，在计算时不考虑摩擦力等因素，直观的反应出各构件的静态受力。在已知机构凸轮T1的扭矩，以及四连杆机构各点的静态位置，求施加在灭弧室上的力F5，以下分别用三角函数计算和新的简便方法计算（为了方便叙述就称其为“测量法计算”）。

（1）三角函数计算

三角函数计算采用大量的三角形作图，从T1一步步推算到F5。那么我们下面采用直角三角形作图，利用函数的方法一步步分解去计算各转点上的扭矩和力。下面我们利用三角函数和图解的方法进行去推算各扭矩和力的表达式。

当机构凸轮在扭矩T1的作用下，呈逆时针旋至一定角度，在与输出拐臂上的滚轮刚接触点时（设接触点为B），其整体静态受简图见图2。利用B点和圆心A点连线就可以得到受力方向F1，直线AB两端延长，分别与O1和O2形成两个直角△AO1J和△O2KB。见图3。作用力F1=T1/（AO1×sina1）;作用在O2的扭矩T2=F1×（sina2×O2B）;同理，将直线CD两端延长，形成两个直角△O2LC和△O3MD。见图4。作用力F2=T2/（CO2×cosa3）;作用在O3的扭矩T3=F2×（sina4×O3D）;同理，按此方法直接可计算出F3和T4，最终可计算出F5。见图5。F3=T3/（cosa5×O3E）;F4为分闸弹簧的作用力，在机构凸轮的作用下，使支点O4呈逆时针旋转，必须要克服F4施加在支点O4上的扭矩。那么，T4=F3×（sina6×FO4）-F4×（sina7×GO4）;最终求得F5=T4/（cosa8×O4H）;为了体现F5完整表达公式，整合以上公式就可以得到推理公式;F5= [T1/（AO1×sina1）×（sina2×O2B）/（CO2×cosa3）×（sina4×O3D）/（cosa5×O3E）×（sina6×FO4）-F4×（sina7×GO4）] /（cosa8×O4H）    公式①。

（2）测量法计算

上述三角函数的计算方式，我们发现其有一定的规律，角度乘以臂长就可以得到受力方向与支点中心垂线的尺寸。因此，只要明确了其受力方向，我们可以直接在图上可以测量出各垂线的尺寸，利用乘除就可以得到完整的推理公式。设各垂线为L1～L8，见图6。为了简化过程，各个作用力和扭矩不再进行详细的推理，只要推理出作用在F5上的力即可，可利用以下公式就可以得到F5的表达式。

F5= [T1/L1×L2/L3×L4/L5×L6-F4×L7] /L8  公式②;

（3）參数验算

为了证明其公式①和公式②两者计算的一致性，假设凸轮上的扭矩和分闸弹

簧上的力值已知，各直角三角形斜边和角度从CAD简图测量得出，利用公式①求出各构件的静态受力情况。已知T1=40000N.mm，F4=450N，a1=26°，a2=53.7°，a3=9.5°，a4=27.3°，a5=20.2°，a6=85°，a7=48.3°，a8=3°，AO1=35mm，O2B=35.4mm，CO2×=40mm，O3D=40mm，O3E=40mm，FO4=50mm，GO4=76mm，O4H=40mm。把已知参数代入公式①中，得到F5=[40000/（35×sin26°）×（sin53.7°×35.4）/（40×cos9.5°）×（sin27.3°×40）/（cos20.2°×40）×（sin85°×50）-450×（sin48.3°×76）] /（cos3°×40）=506.6N。

按测量法来进行计算的话，仅测量出垂线的长度即可。已知T1和F4，L1=15.4mm，L2=28.5mm，L3=39.5mm，L4=18.5mm，L5=37.5mm，L6=49.8mm，L7=56.7mm，L8=40mm。把已知参数代入公式②中，得到F5=[40000/15.4×28.5/39.5×18.5/37.5×49.8-450×56.7]/40=513.2N。

同一种静态传动受力图，采用以上两种计算方法所取得结果是一致的。

三、结论

在已知的传动静态受力图中，各个传动受力值和扭矩都是可以按上述两种方法进行验算的。相对于利用三角函数的计算，过程繁锁。采用受力方向与臂长夹角的角度和臂长的关系，计算出垂线的尺寸，在此过程中容易出现计算错误，对工程设计人员效率不高;而采用测量法来计算，只要确定了垂线的尺寸，省略了角度和臂长关系的计算，具有更加简便、高效的计算方法。

参考文献

[1]徐国政，张节荣，钱家骊，黄瑜珑.高压断路器原理和应用[M].北京：清华大学出版社，2000.

[2]苑 舜.高压断路器弹簧操动机构[M].北京：机械工业出版社，2001.

[3]林 莘.现代高压电器技术[M].北京：机械工业出版社，2002.