借助几何直观培养学生空间数感策略探究

黄福龄

摘要：借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中发挥着重要作用。建立数感有助于学生理解现实生活中数的意义。质量观念、空间观念都属于数感的范畴。立体图形的多面性和抽象性对于小学生来说有一定难度，为了突破这个难点，教师可借助几何直观，帮助学生建立空间观念。

关键词：几何直观;空间数感;数学教学

数感作为新课标中的十大核心概念之一，新课标将其定义为一种感悟。这既包括感知又包括领悟，既有感性思维又有理性的思维。建立数感有助于学生理解现实生活中数的意义。质量观念、空间观念都属于数感的范畴。

学生在一年级认识了立体图形后，在五年级下册开始认识体积和体积单位，并学习计算图形的体积。立体图形的多面性和抽象性对于小学生来说有一定难度，为了突破这个难点，教师可借助几何直观，帮助学生建立空间观念。有了空间观念还不够，培养学生对抽象的三维空间的数感，有利于学生快速对几何空间问题的判断和决策，从而培养数学学科素养。下面以体积单位的认识和体积的计算教学为例，探讨借助几何直观对于建立空间数感的意义。

教学片段一：一粒粒的体积单位

师：我们知道物体的体积有大有小，计量长度，我们用一条条的长度单位——厘米、分米等;计量面积，我们用一块块的面积单位——平方厘米、平方分米等;那么计量体积又用什么单位好呢？

生1：用体积单位：立方厘米、立方分米、立方米等。

师：你见过体积单位吗？它长什么样的？

生2：1立方厘米有这么长（学生用食指和大拇指夹住1厘米左右的长度）。

生3：1立方厘米有指甲这么大（学生举起大拇指说）。

生4：不对不对，那是测量长度和面积的单位，测量体积的单位应该是一粒粒的，好像是一个正方体。

师：有道理吗？（学生点点头）那么1立方厘米是一个怎样的正方体呢？

生5：应该是棱长1厘米的小正方体。

师：观察一下，你身边有大约1立方厘米大的物体吗？

生6：骰子、橡皮、大拇指头。

教师出示课件：如果下面的图形都是由体积是1立方厘米的小正方体堆砌成的，那么下面各图占的空间有多大呢？

【评析】以上是让学生认识一立方厘米的教学片段，在师生的深度对话中，学生进行了深度思考。在教学过程中运用了迁移、对比、直观、想象的教学方法，让学生建立起体积单位的概念。从生2和生3的回答可见，有学生对单位的认识还停留在平面上，没有上升到立体空间，而且对平面和立体的数感容易混淆。因此教学中宜用教具1立方厘米和身边熟悉的参考物，充分建立1立方厘米的表象。让学生直观感知：长度单位是一条条的、面积单位是一块块的、体积单位是一粒粒的。确定了标准，然后根据标准去测量物体的体积。让学生积累数空间里的体积单位的经验，这是培养学生空间数感的起点。如果学生深刻地认识了1立方厘米，那么就不难理解1立方分米和1立方米了。对于抽象的1立方分米和1立方米，也可以借助几何直观，寻找学生身边熟悉的物体作为标准，让学生记住体积单位的表象。体积单位观念的建立，有利于日后佶算物体的体积的大小，从而培养空间几何的数感。

教学片段二：数出来的体积

一、趣味导入

1.我拼你说

（1）教师出示用棱长1cm的正方体搭成的不规则立体图形，学生通过数一数口答图形的体积。

（2）如果搭成规则图形长方体和正方体，有更快的数出体积的方法吗？让学生说说数得快的方法，初步渗透长×宽×高的方法。

（3）出示被遮挡的长方体让学生说体积，以突出只需要关注长方體的长、宽、高的数据。

2.情景设疑

（1）没有方块提示，直接问一个长方体的体积是多少。

（2）学生需要借助方块测量、切割吗？如果玉石不能切割，有其他办法吗？

【设计意图】通过数体积单位来计算体积的方法，培养学生的空间观念，让学生感知规则图形的体积的计算方法是有规律的，引导学生探究规则图形的体积计算的规律，也就是体积的计算方法。

二、推导公式

1.猜想：量出它的长、宽、高的数据就可以计算。是不是所有的长方体的体积都可以用长乘宽乘高来计算呢？

2.验证。

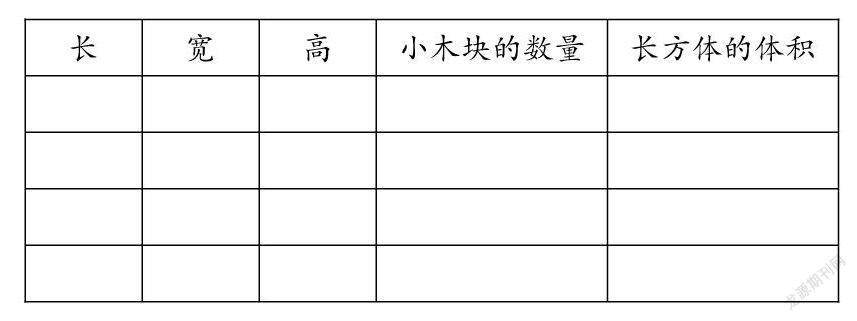
（1）小组合作，用准备好的12块1cm的小正方体，任意摆出不同的长方体，然后把数据填入下表。

（2）通过实验进一步验证：无论怎么摆成长方体，长方体的体积都正好等于长方体长、宽、高的乘积。

归纳：长方体的体积=长×宽×高（如果用字母V表示长方体的体积公式可以写成V=abh）

【设计意图】让学生动手操作，合作探究长方体的体积的计算的规律，渗透归纳推理的思想方法，总结规律，形成模式，即计算公式。

【评析】如果立体图形的体积都可以看作这个图形是用体积单位堆砌成的，那么任何立体图形的体积的测量和计算都可以通过数体积单位而得到结果，只是规则图形有更快的数的方法，并形成规律，即公式，而计算不规则图形的体积可以用估测或排水法等等。曾经对一个班的学生做过调查，有97%的学生知道用长×宽×高可以算出长方体的体积，但只有58%的学生知道为什么可以用长×宽×高算出体积，大部分学生觉得如果不知道长、宽、高就无法计算体积。这说明了教学过程中如果太强调公式计算的好处，则会忽略了本质，导致很多学生只知道计算公式，并不知道为什么这样算，对公式进行变式就无法算，所以教学要追本溯源。长度用长度单位测量，面积用面积单位测量，体积用体积单位测量，所以通过数体积单位知道物体的体积是通法，适用于任何图形。学生在数体积单位的过程中，发现有的规则图形，如长方体、正方体，可以有更快的数的方式，就是先数一行有几个，再数一层几个，再乘层数就能快速数出它占的空间有几个体积单位，因而得出长方体的体积跟它的长、宽、高有关。教师在教学中借助几何直观图，让学生积累从直观数据到抽象概念或模型的活动经验，能帮助学生从本质上掌握概念的意义或解决问题的方法，而不是表面的简单记忆。

学生空间观念方面的数感建立了，就不会盲目用公式计算物体的体积，而是从物体的长、宽、高三维数据去分析物体所占的空间大概有多少去解决问题。如常见问题：把一块长12厘米，宽5厘米，高4厘米的石头装在长8厘米，宽8厘米，高5厘米的长方体礼盒里，装得下吗？

生1：石头的体积是12×5×4=240（立方厘米）礼盒的体积是8×8×5=320（立方厘米）礼盒的体积>石头的体积，所以装得下。

生2：因为石头的长、宽、高的数据与礼盒的长、宽、高相比，其中礼盒的长8厘米<石头的长12厘米，所以装不下。

可见，生1是对长方体的体积计算方法停留于表面记忆，并不理解，更谈不上空间观念上的思考。而生2则从几何空间思考立体图形的三维数据进行合理分析问题。二者区别在于理解和不理解，有空间观念和无空间观念的机械计算。因此，对于几何空间的概念或计算方法的起始课，很有必要借助几何直观，帮助学生建立空间观念和空间上的数感。

“数感”在数学学习上是非常重要的必备素养，而空间几何图形的数感对于仍停留在直观思维较多的小学生来说是比较困难的，为了突破这个难点，教师可借助几何直观，增强学生理解空间的数据特点，建立空间观念，培养空间数感。综合上面的教学例子，进一步说明建立空间观念和培养数感的重要性，正如《课标》所说，对于几何图形一类的教学同样适用。