回到本真，回到简约

林颖勤

肖慧老师，言不多，行干练，就如她的教学风格一样“简”、一样“真”。她所言的“求简，求真，求深”，是对数学核心素养课堂的思辨，对数学教育真谛的追求，它能使数学教育回归本真，让学生获取真知真能。在研究与实践中，笔者再次获得新的认识：教育教学中的简约，既是一种策略又是一种形态还是一种境界，其本质就是要遵循教学规律和人的成长规律，以达到教学最大效益的育人功能。笔者在数学课堂上也常思考：学生到底需要怎样的数学？怎样的数学课堂才能唤醒童真童趣，让学习回到本真、让教学回到简约？下文结合实例谈谈笔者的粗浅经验及做法。

一、数学，“简单”又好玩

一提到数学，不少学生都会想到“枯燥…‘恐怖”“焦虑”等词语。作为一线教学工作者，我们一直在努力挖掘数学的真，展现数学的美，催生教学发生本质的变化，让数学不再“可怕”。

（一）学科融合。锻炼思维

六年级下学期的学生进入总复习阶段时，旧知再探显得“翻热饭菜”无味道。基于活跃课堂、呼唤学生的童心，笔者设计了这样一道题目：不允许使用梯子、凳子，请测量教室的容积。不出所料，学生一下子就合作完成了测量教室长、宽的数据，面对着教室的“高”，究竟如何出手呢？数学的魅力，就在于让学习成为当下解决实际问题的需要，学生在想法子的同时需要打破学科的界限，让学科交流、融合。然而，面对着新的任务，学生你一言我一语，这也是展示小组合作学习的最佳时机。以下为小组内的讨论片断展示：

生1：我们可以搭人梯，一个接一个，然后用软尺进行测量！

生2：太危险了，何况题目里规定不能使用梯子！

生3：我们用棍子绑好，顶在天花板，再测量棍子的长度。

生4：去科技室借用小飞机粘上丝带飞上天花板，再测量丝带的长度。

生5：用手机将课室的墙壁拍下，然后测量。

讨论一度陷入困境，师感叹：“如果我们能飞上去就好了！”话音刚落，不知哪个角落传来了一个小声音：“我们找科学老师去！可以利用氢气球帮我们飞上去测量啊！”整个数学课堂就这样被“翻转”了。于是，延伸到第二节课，学生请来了科学教师。玩过氢气球的学生有一定的认识，但对于为什么“氢气球能飞上天而空气球不能”就一片茫然。为此我们进行了氢气性质的知识拓展。学好了方法，接着又如何开始实施呢？“需要有步骤，不然就乱了。”学生经过思量，小组再次合作，尝试做学习单，集体分享后再修改学习单。集思广益，最好优化方案：将绳子拴在氢气球上——测量气球的长度——测量绳子的长度——把气球和绳子长度加起来。在测量过程中，学生习惯性进行分工合作、兴致盎然。“畦，畦，成功飞天啦！”随着一声声惊叹，两个气球同时成功地飞到了天花板，研究的热情加溫了。学习单、黑板很快被写满数据。学生自己反思：“为什么每组数据相差那么远呢？”在稚嫩的笑声中他们发现了：“我们组的气球结没有打好，漏气啦！”“我们在测量气球的高时每放好尺子，测偏了。”“哈哈，你们组漏加气球的长度啦！”……

欢声笑语中，谁还觉得“数学可怕呢”？

陶行知先生认为，在做中教乃是真教，在做中学乃是真学，“教学做合一”的思想就是强调学生需在实践中去追求真理。这样的学科“混搭”，让学生收获了快乐、锻炼了思维，也验证了肖慧老师“学为中心，提升素养”的教学主张。

（二）游戏融合。拓展空间

教学的空间决定了学生发展的可能，给学生思考的空间、表达的空间、交往的空间、实践的空间。然而，有学者做了这样的比喻：在两米高的小屋里，篮球运动员姚明再怎么努力也无法站直，因为他的头早已顶住了天花板。试问在教学领域，教师对学生发展的“天花板”却可能视而不见：小步零碎的提问、过于细腻的指导、以熟练为目的的刷题训练等，这些直接禁锢了学生应有的数学思维。那么，“怎么教”也决定了“教什么”。狭窄的小屋，学生还能挺起自由思考的脊梁吗？

笔者认为，如果将数学学习活动与学生的生活密切联系，不仅可以帮助学生真正理解数学内容，也能够促进学生运用已有的经验实现“冲破天花板”的可能性。那如何将有趣的游戏与数学融为一体展开教学呢？下面，笔者以《亿以内数的认识》为例进行分析。

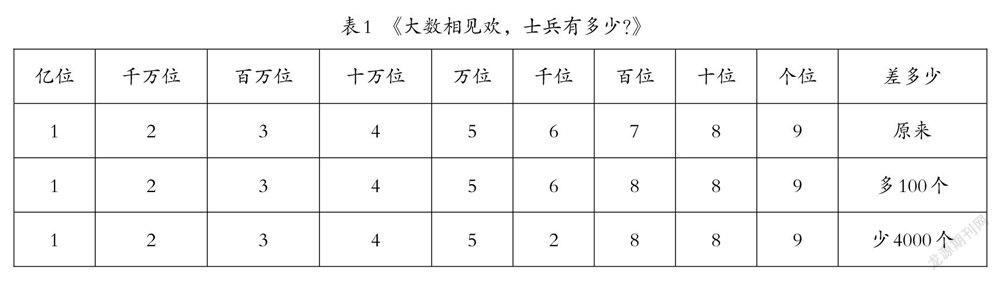
1.每个数位站一位拿着数字卡片的人，另派一人拿着数字卡片与个位的人猜拳。猜赢后，和拿十位的人猜拳，直到猜输为止，就把数字卡片交给下一位，取代其的位置，形成新的多位数。

2.新的数与原来的数相差多少，写在记录卡上。（见表1）

3.根据表格回答问题：

（1）“多100个”是指将军在哪个数位上猜输了？

（2）“少4000个”是指将军在哪个数位上猜输了？

这个游戏融入了亿以内数的认识的相关知识。学生可以自己制作数位卡片，进行分组，全班参与。台上的学生进行游戏，台下的学生进行记录，并比较原来的数与新产生的数之间相差多少，从而让学生在玩游戏的过程学习写数、读数，理解各个数位表示的意义以及两个数之间的计算。

学科整合、数学游戏用简单的方法表达数学，就是复杂问题简单化，使用适合学生亲近数学、学好数学的教学方式，是更为成功的教学。

二、数学，在互动中趋向“深度”

我们常发现，课堂上教师讲解多、学生自主探索少的现象普遍存在。公开课上生生互动很流畅，殊不知这种形式都是课前经过精心安排、反复训练来达到教师预设的目标。这样的互动深度不够，没有给学生留下思考的空间和时间，学生像表演节目一样，缺乏辨析、质疑能力。大部分学生学习较为被动，获取知识常用“拿来主义”，没有推动和创造。为此，笔者以《年、月、日》为例大胆尝试放手，结合实情，在小组合作学习中将问题暴露出来。

学生通过动手实践、自主探索，进行了非常有个性的实践和想法。经过小组内达成共识，上台展示如以下任务卡。（见表2）

“学为中心”的课堂是学生做主人的舞台。学生敢于提出质疑，表达自己的想法和疑惑，生生之间相互辩论解答，激起学生的思维碰撞的火花，是数学课最美丽的生态之花。这样的课堂源于教师巧妙地提供舞台，引导学生大胆质疑交流，教师要沉得住气，善于把学生的质疑交给学生自己去解决。

师：大家讨论得真激烈，哪个小组代表上来分享分享？

生1：我代表我们小组上来汇报，我们小组研究的是2005年至2008年，我们发现每一年的1月、3月、5月、7月、8月、10月、12月有31天。然后每一年的4月、6月、9月、11月有30天，就只有2月不同，2月有时候是28天，有时候是29天。

生2：因为我们发现2008后面的8能被4整除，其他的后面不能被4整除。能被4整除的是闰年，闰年的2月就有29天，平年的2月就有28天，平年就是不能整除4的。

师：真是丰富啊！同学们听完汇报有什么想问？

生3：请问，为什么只是被4整除，而不是被5或被6整除呢？

生1：4的话，因为闰年四年才有一次。我的直觉认为除以4才有闰年。

生4：如果是2016年呢？

生1：2016年也是可以被4整除的。

生5：你的直觉有依据吗？

生1：……

生6：我听说是跟地球绕太阳公转有关。

生2：图书角课外书上有介绍，你可以看看。

生7：为什么有一些是31天，有一些是30天啊？

生1：我也不知道，估计是这样分配的吧。

生8：为什么只把2月份定为28或29天，而不是3月呢？

也许学生的对话较为零散、幼稚，然而，核心问题就在学生的追问中，思维的碰撞中越辩越明。这不就体现了肖慧老师的主张“学为中心”的课堂，并不拒绝“教”，而是教学设计做减法，学生活动做加法，教师通过更高水平的教来促进教学了吗？相信坚持下去，学生才会既乐于质疑又善于质疑，进一步内化思考，使学习的层次更趋向深度学习，对话更有质量。

三、数学。是文化的沉淀

《数学课程标准》指出：数学是人类的一种文化，它的内容、思想、方法和语言是现代文明的重要组成部分。因此，数学课堂教学不应只有抽象的数字、符号、运算和图形，不应只是传授数学知识，还应当让数学文化走进小学数学课堂，使学生受到数学文化的熏陶，品味数学文化的魅力，提高数学文化素养。

（一）数学文化，培植数学情怀

将数学史引入课堂，笔者的做法是经常带着学生欣赏古今中外的数学史料，祖冲之、阿基米德、高斯、华罗庚等数学大师，成了学生经常讨论和崇拜的人物。笔者在教室里开辟一块数学角，为学生创设数学文化的氛围，为学生提供表达的园地。特设“数学小擂台”“数学故事大王”，每周一上午数学课堂由不同的学生讲述自己眼中的数学，分享自己课外的数学知识和趣事，讲述自己崇拜的数学名家故事等等。

如当学生学习了《比的认识》一课，周末布置小任务：1.上网寻找“黄金比”的资料;2.你能用比的知识解释“为什么女性总爱穿高跟鞋吗？”。对于《圆的周长》的课外学习，学生的学习热情更高涨，惊叹于中国古代人民的伟大与智慧的同时，小组之间不约而同地展开背诵“圆周率”的小竞赛。学生沉浸在数学文化中，思维已飞越了课堂、跨越了时空，萌生了探寻数学世界的积极情感。

（二）理性精神，涵养数学气质

理性精神是数学文化的核心。理性，体现在数学追求一种完全确定、完全可靠的知识。著名华裔数学家丘成桐先生说“学数学是要有一点气质的”，笔者以为，这种气质乃理性精神无疑。数学课堂需要重视数学理性精神的涵养。下面，以《能被2、5整除的数的特征》一课，谈理性精神的落地。

师：为什么判断一个数是不是5的倍数，只要看个位？独立思考、同桌交流之后全班交流。

生1：我发现5的倍数末尾一定是0或5，而这两个数除以5正好没有余数。

生2：奇数乘5，它的个位一定是5;偶数乘5，它的个位一定是0，没有其他情况了，所以只看个位。

师：以上说的都是为什么看个位，而不是“只看个位”。

生3：如果去掉个位的话，就是一个整十、整百、整千数……这些数一定是5的倍数，所以十位就不用管了。

师：谁听懂了他的想法？

生4：他的意思是，减去个位余下的数，个位一定是0，它能被5整除。

师：很好！谁能结合例子或教具进一步说明？（呈现计数器）

生5：在计数器的十位上拨2，表示2个10，20是5的倍数，所以十位上的2不影响结果。

生3：当个位是0，我在十位上任意拨，它们都是5的倍数。

生6：在百位、千位上任意拨，它们都是5的倍数，因为它们的个位都是0。

生7：一个数可以分成两个部分，十位以上的部分必然是5的倍数，所以不用考虑;个位这个部分不确定，只看个位就好了！

师：数学是讲道理的，同学们都是讲道理的数学人！

数学课堂是传承理性精神的主阵地，引领学生尽力去探求和明晰知识的最深刻最完美内涵，培养探究欲望和勇气，是我们始终为之努力的目标。

焕发学生的学习本能，让学习回到本真，让教学回到简约，我们期待遐见更美的數学。