“学生说题”

刘黎明

摘要：“学生说题”教学法是近几年在教学改革与长期教学实践中涌现出的一种新型双边教学模式，是提高学生解题能力和自主学习能力的有效措施。同时，在这个过程中也能极大地提高学生的学习热情，发展学生的核心素养。本人于2019年加入福州市教育科学研究“十三五”规划课题——《探究中学生的数学说题能力的培养》。文章以一道题为例，展示如何在教学中有效地开展“学生说题”教学法。

关键词：学生说题;过程;思维;解题能力;自主学习能力;数学技能

中图分类号：G633.6 文献标识码：A 文章编号：1672-1578（2019）02-0168-01

1.试题呈现

题目：根据要求解答下列問题：

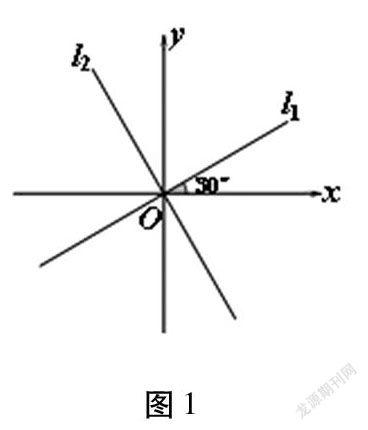
如图1所示，过原点的直线11向上的方向与轴的正方向所成的角为30°。

①求直线L1的函数解析式。

②把直线L1绕原点O逆时针方向旋转90°得到直线L2，求直线L2的函数解析式。

2.说明

本题是布置给八年级学生在探究课《探究：平面直角坐标系中的90°旋转》的课后作业中，通过探究课的学习后，学生掌握了：对于解决平面直角坐标系中的90°旋转问题的核心方法是：（1）图形的旋转转化为点的旋转（化繁为简，转化的思想和方法）;（2）向坐标轴作垂直，构造全等的直角三角形（构造K型图）。

3.学生说题过程

3.1说题目背景

（1）题材背景：该题目是平面直角坐标系中求过原点的直线的函数解析式的问题。

（2）知识背景：该题目涉及的知识点有：①用待定系数法求正比例函数的解析式;②直角三角形中，30°锐角所对的直角边等于斜边的一半;③勾股定理;④平面直角坐标系中的90°旋转;⑤一线三等角模型的直角三角形全等的判定以及全等三角形的性质。

（3）思想方法背景：数形结合思想，转化、化归思想。思路来源：

①几何问题归结为代数问题（化归思想）：通过分析得出过原点的直线L1的函数解析式实质就是正比例函数解析式，因而只要再想办法在直线L1上找到符合条件的一个点的坐标，就可以利用待定系数法加以求解;

②数形结合思想：本题要充分利用30°这个条件，以及平面直角坐标系中的坐标的寻找通法：向坐标轴作垂直，结合这两点不难想到可以添加辅助线后构造一个有30°的直角三角形，再利用：直角三角形中，30°锐角所对的直角边等于斜边的一半和勾股定理，求得坐标，从而代人得解。

思路来源：

③转化思想（直线的旋转转化为点的旋转）：把直线L1绕原点O逆时针方向旋转90°得到直线L2，实际上可以看作是直线L1上的点A绕原点O逆时针方向旋转90°得到直线L2上的点A'，因此只要利用探究课中得到的核心方法，向坐标轴作垂直，构造构造全等的直角三角形（构造K型图）。接下来就是一线三等角模型的直角三角形全等的判定以及由全等三角形的性质得到的相关线段的长度。从而得到点A’的坐标，然后再用待定数法轻松解决。

3.4说反思或心得

本题是平面直角坐标系背景下的问题，笛卡尔在他的著作《几何》中向世人证明：一切几何问题都可以归结成代数问题，也可以通过代数转换来发现、证明几何性质。因而凡是以后碰到图形的旋转，我们都可以采用化繁为简，把图形的90°旋转转化为点的90°旋转，碰到平面直角坐标系的问题都尽可能通过构图法中运用数形结合的思想。

总之，课堂教学中实施学生“说题”教学法，充分体现新课程的指导思想和理论，在这个过程中，不仅能提高学生的解题能力，更有利于学生创造性思维能力的训练，是学生生命力的绽放，从而能提高学生的自主学习能力，同时它能减轻学生负担，能促进教师的专业成长。教师在平时的习题课和试卷讲评课中，应该充分利用学生“说题”教学模式，让学生真正走出“题海”，走向成功。