运用画图策略培养儿童几何直观

王静

【摘要】数学教学改革重视儿童几何直观的培养，它能帮助学生打开思维的大门，开启智慧的大门，突破数学理解上的难点。因此，这就要求教师在教学时，让学生在动手画图中培养几何直观意识;在多种图形模型中，提升几何直观理解;在反思内化积淀中，发展几何直观思想。

【关键词】画图策略 儿童 几何直观

“几何直观”是《义务教育数学课程标准（2011年版）》提出的十大核心概念之一。虽然，小学数学教材中没有出现“几何直观”的定义，但小学数学诸多问题的呈现、分析等过程充分体现了“几何直观”的作用和价值。数学和数学教育家弗赖登塔尔也曾说：“几何直观能告诉我们什么是可能重要、可能有意义和可接近的，并使我们在课题、概念、方法的荒漠之中免于陷入歧途之苦。”因此，笔者一直在思考，在小学阶段如何运用画图策略培养儿童的几何直观？

一、重视画图，培养几何直观意识

数学中的“几何直观”究竟指什么？数学家克莱因指出，“数学不是依靠在逻辑上，而是依靠在正确的直观上，数学的直观就是对概念、证明的直接把握。”《义务教育数学课程标准（2011年版）》中也指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。”这段阐述明确指出图形是培养儿童几何直观的重要载体。因此，笔者认为，培养儿童的画图意识，运用好画图的策略对培养儿童几何直观能力有着重大意义。

1.低起点：以图求解——变模糊为清晰

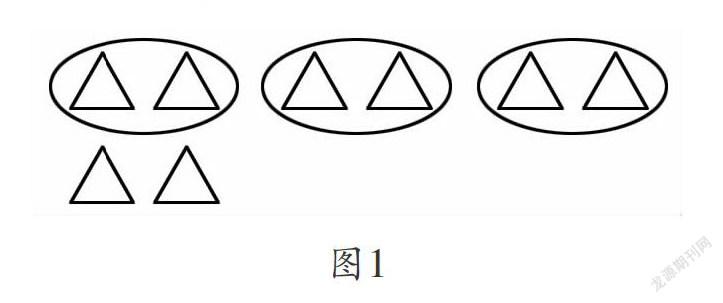
儿童的认知发展一般经历三个阶段：动作感知—形成表象—建立概念。而在小学阶段，画图的做法就符合這一规律，将抽象的思考对象“图形化”。教师培养学生画图首先从低起点开始，通过简单的图（图形直观、简洁）让儿童体会。如三年级在学习“倍数”的知识时，教材中对“什么是倍”并没有给出语言定义，而是通过简单的图（如图1）画一画、圈一圈的方法感受“倍”的含义。那么，运用这样的直观教学，将“6是2的3倍”这样的文字表述借助图形就能解释得清晰明了：每2个是一份，有这样的3份，就是2的3倍。模糊的“倍”与清晰的“份数”相结合，学生就能直观感受到画图的重要作用，为画图意识的培养助力。

2.慢渗透：以形助数——变抽象为具体

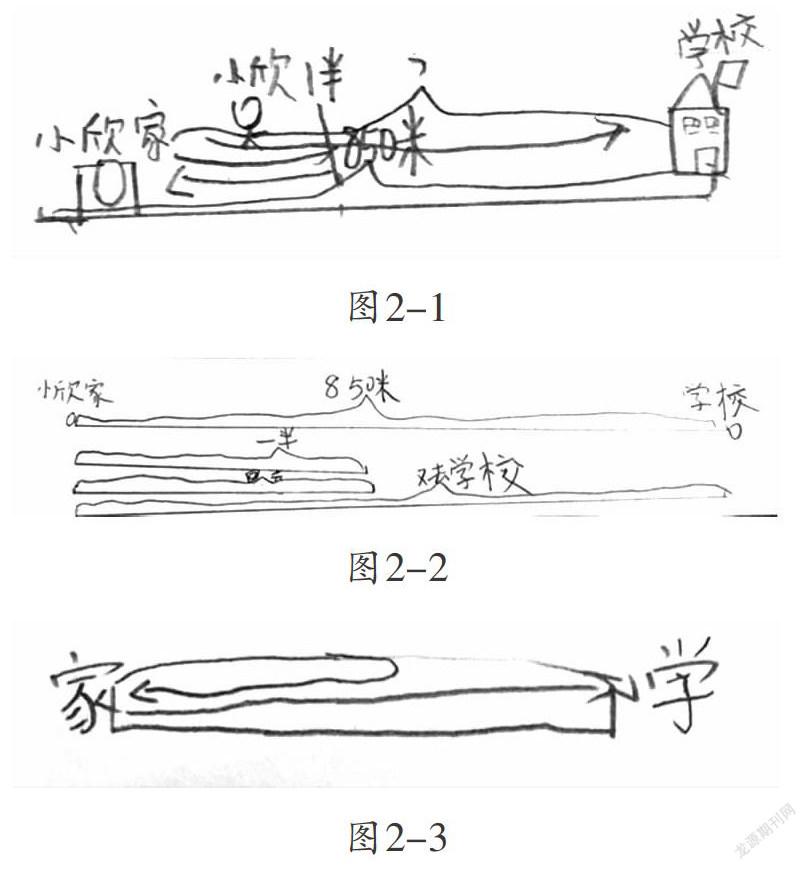
数学家华罗庚对“数”与“形”有过非常精辟的刻画：形使数更直观，数使形更入微。数形结合作为一种重要的思想方法，是把数学问题中的运算、数量关系等与几何图形和图像结合起来思考，从而使“数”与“形”优势互补，展现逻辑思维与形象思维的完美统一。在苏教版三年级上册第一单元中有这样一道思考题：小欣家离学校850米，一天早晨，她从家出发去学校上学，大约走到总路程的一半时，发现忘记带数学书。于是又回家拿书，再去学校。这天早晨，小欣上学大约一共走了多少米？

笔者对学生们提出如下要求：你能把小欣上学的过程在本子上画下来吗？以下三幅图是学生的代表作品，图2-1将学校、小欣家还有人物都画了出来，数学里透露出童趣;图2-2用小圆圈代表学校和小欣家，将线和“一半”“回去”“又去学校”这些关键词相结合，这是从抽象到半抽象的一次转变;图2-3是一幅常见的线段图，学生已经不再借助房子、小人、圆圈来表征信息，几条线就已经将条件表示得清清楚楚了。这三幅图从稚嫩到成熟，层次不一样，但学生们的几何直观都得到了发展。

学生从低起点的感知到逐渐渗透，用画出来的“形”来刻画和解释数学知识，感受到几何直观的价值，渗透几何直观的意识。

二、丰富模型，提升几何直观理解

图形有助于将抽象的数学对象直观化，利于培养儿童的数学直观领悟能力，而图形模型的建立则是从若干具体情境中抽象出问题的本质，全方位培养儿童几何直观理解能力及初步的模型思想。以下介绍两种在小学阶段常见的画图模型。

1.线段图模型

小学一年级起，教师就应该有培养学生画示意图的意识，3可以画成3个△。在苏教版教材中，学生第一次正式认识线段图是在三年级，用来表示数量之间的关系，帮助学生分析并解决问题。

如四年级下册“解决问题的策略”是解决和差问题。学生读题获取数学信息：两人共有72枚邮票，小春比小宁多12枚，求两人各有多少枚邮票。这时，教师提问：你能想到什么办法帮助我们直观地、很清楚地看清数量之间的关系吗？还有能找到解决问题的办法吗？同学们纷纷回答：画线段图。在教师的引导下学生读懂书中的半成品线段图（如图3），并且补充完整信息，解决问题。

在小学阶段，和差、和倍、差倍问题，还有行程问题等，都可以用线段图厘清数量关系，学生的认知难点得到了突破，问题得以解决。因此，在小学阶段，画线段图是非常重要的解题策略。

2.面积图模型

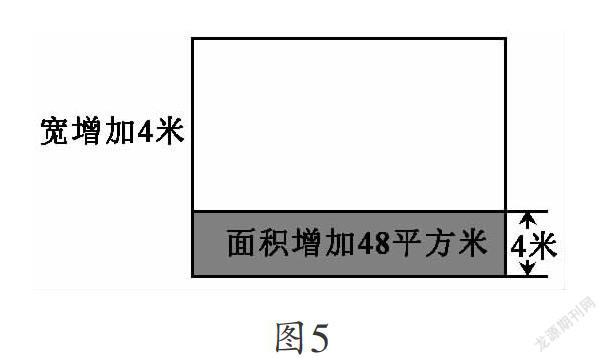
画面积图是解决问题的另一种策略。学生利用面积变化图将一些表述复杂、晦涩的文字变得直白形象，从而有效地分析条件，探寻出解题路径。在四年级学习“画图解决问题的策略”时，教师出示这样一道题：李镇小学有一块长方形试验田。如果这块试验田的长增加6米，或者宽增加4米，面积都比原来增加48平方米。你知道原来试验田的面积是多少平方米吗？此题条件较多，光靠想象无法准确解决问题。画出面积图就能很直观地看出题意（如图4、图5），图4描述的是“长增加6米，面积比原来增加48平方米”这一条件，由此可以求出原来长方形的宽=48÷6=8（米）;图5描述的是“宽增加4米，面积比原来增加48平方米”，从而可以求出原来长方形的长=48÷4=12（米）。

三、内化积淀，发展几何直观思想

几何直观能力的培养不是一蹴而就的，必须经过长期的、有意识的训练。学生在运用多种图形模型解决实际问题的过程中可以积累丰富的数学画图经验，体会画图策略的价值，并形成自觉地应用，进而发展其数学思想。

1.借形观数，多元表征，积累直观经验

教师在教学中把几何直观运用得越充分，直观的效果越明显，学生的直观表现意识就会越强烈。如在教学12×14这样的两位数乘两位数的笔算时，教师通常会从情境出发，引导学生理解算理：12×4和12×10分别表示的意义，进而厘清算法。而当教学时呈现直观模型图（如图6）后，学生对直观的理解也就更加深刻。

所以，借助图来直观表征数学计算问题，理解两位数乘两位数的算理，在图与式的勾连中，让学生深刻理解算理，体会两位数乘两位数的本质：乘法意义与乘法分配律。强烈的直观表征，会为发展和形成几何直观思想奠定坚实的基础。

2.借形思法，联想顿悟，发展几何思想

借助几何直观图，学生可以进行推理、演绎以获得一些解题的一般思路。而当学生的几何直观能力发展到一定水平时，学生还能够独辟蹊径，直观顿悟出一些特殊的方法，形成创造性的解题思路。如教学六年级上册“长方体和正方体的认识”这一单元时，教师根据题目提出问题：水箱高度是水面高度的3倍，这个水箱还能盛水多少升？学生根据题意画出直观图，标好有关的条件数据（如图7）：

一般情况下学生能找到常规的思路和方法“水箱的体积-水的体积”，用50÷（5×5）=2（分米），2×3=6（分米），5×5×6-50=100（升）。但也有学生从图中就直接顿悟出50×2=100（升），这表明学生经过长期的几何直观能力训练后，已经能借形思法，实现顿悟。

综上所述，几何直观能力的培养离不开画图策略的运用。作为一线教师，需要钻研教材，帮助学生养成画图意识，逐步培养他们运用几何直观来描述和分析问题的能力，进而提升学生的数学素养。♪

【参考文献】

[1]吴正宪，刘劲苓，刘克臣.小学数学教学基本概念解读[M].北京：教育科学出版社，2014.

[2]曹培英.跨越断层，走出误区：“数学课程标准”核心词的实践解读之六——运算能力（下）[J].小学数学教师，2014.

[3]陈涛清.培养小学生几何直观的策略及思考[J].小学数学教育，2012（12）.