善用启发式教学培养数学思维的策略探究

崔链松

摘 要：我国教育家陶行知先生说过：“人人是创造之人。”他提倡创造思维的教育，提倡激发学生的创造力。因此，作为一名教师，不能只为教学而教学，必须担当起激活学生思维的重担。笔者就多年初中数学教学的实践经验来谈一谈培养学生思考能力的若干观点以及如何通过培养学生自主思考的能力以达到解放思维束缚的目标。

关键词：初中数学;启发式教学;数学思维

数学既是学习和研究现代科学技术必不可少的基本工具，也是一門培养和提高人类思维能力的重要学科，而自主思考是培养数学思维的必由之路。《义务教育数学课程标准（2011年版）》（以下简称《数学课程标准》）提出：“数学教学活动应激发学生兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维。”从新课标的基本理念可知，培养学生自主思考的能力远比简单地灌输知识来得重要。那么在实际教学中教师如何培养学生自主思考的能力呢？笔者认为可以从以下几方面入手：

一、引导学生课前学会思考

俗话说：“好的开始是成功的一半。”预习是课前准备的一个重要环节，在学生获取新知中起着探路作用。假若预习环节做好了，学生理解新知就会变得容易，在有自己看法的前提下，可以开拓思维。大部分学生学习会有一定的依赖性，被动地接受教师讲授的知识。教师应当适时地为学生指引思考的方向。比如，《多边形》一课的预习，教师可以提这样一个问题：三角形没有“边”字，那么三角形是否属于多边形呢？学生从小就开始接触三角形，当教师提出这样一个简短易懂的问题时，他们马上议论纷纷起来。学生会因为好奇心的驱使，急于找到一个正确答案：多边形是指一些线段首位顺次连接组成的平面图形，而三角形则是最简单的多边形。教师课前的一个小小的提问往往能触发学生主动通过预习学会思考问题。课前预习是培养学生思考能力的方法之一，也是提高学生思维能力的重要一环。

二、巧设课堂教学，让学生在思考中学习

（一）问题导入，让学生带着问题去探索新知

教育家苏霍姆林斯基说过：“如果教师不想办法使学生产生情绪高昂和智力振奋的内心状态，就急于传授知识，那么这种知识只能使人产生冷漠的态度，而使不动感情的脑力劳动带来疲劳。”足见新课的引入直接影响着课堂教学的质量。利用问题导入，可使学生以思考的方式自然地进入探索新知的状态，他们迫切参与解决问题的欲望就会增强，从而在新课问题引入中锻炼独立思考的能力，培养探索思维。

（二）精讲少讲，为学生预留自主思考的时间

在课堂教学的过程中，不少教师在授课时越讲越多，形成了“满堂灌”的教学模式。教师讲授过多会直接占用学生练习的时间，剥夺了其自主思考的权利，效果往往适得其反。因此，教师在课堂教学上要合理把握时间，改变过去“填鸭式”的教学模式，做到精讲少讲，腾出更多的时间让学生自主思考、学习，以保证学生的思维得到充分发展。对于比较简单易懂的知识内容要少讲甚至不讲;对于学生容易混淆、难以理解的内容，则需要抓住问题有针对性地进行精讲。

总之，应尽可能多地为学生预留思考的时间，使其多一些自由发挥的空间。只有保证学生自主学习的时间和空间，学生才可以更自由地思考和探索问题，从而促进思维的发展。

（三）分组教学，合作交流激发学生思考的动力

在教改创新的背景下，学校推行“练评讲”教育模式。所谓“练评讲”是指：小组练习——助教点评——教师讲解——小组竞赛。其核心理念是分组学习。教师要做到均衡分组以保证各个小组总体水平相当，这有利于顺利展开讨论学习和小组竞赛。通过分组合作探究，促成同学间主动探究思考问题。在《勾股定理》一课的学习中，笔者以写勾股数为铺垫开展课堂小组议一议、赛一赛，限时看哪个学习小组写出的勾股数最多、最准确。这既巩固了学生对勾股定理公式ɑ2+b2=c2的掌握，也激发了学生在小组合作中探究学习的热情。自从学校实行“练评讲”分组教学模式以来，学生学习的参与度明显提高，课堂上发呆、走神等不良现象大幅度减少，有效调动了学生学习的积极性。在分组学习、组内讨论交流等学习环节，可以凝聚团队力量，相互影响，促进提高，推动学生争相自主思考为团队出谋献策。

（四）联系生活，激发学生思考的兴趣

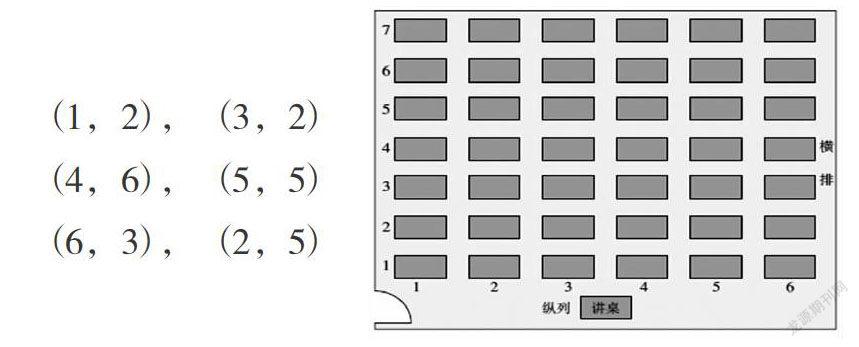
数学相对其他学科较为枯燥乏味，如果教师经常直截了当地传授知识内容，久而久之会让学生觉得疲惫，甚至是放弃学习。《数学课程标准》明确指出：“要重视从学生的生活实践经验和已有的知识中学习数学和理解数学。”在教学实践中，笔者会把数学问题与现实生活紧密联系起来，让学生体会到学习数学的快乐，从而激发他们的学习兴趣。比如在《平面直角坐标系》的教学中，笔者创设了如下问题情境：1. 说说你去影剧院看电影的经历，你是怎样找到自己座位的呢？2. 我们的家乡在地球上的什么位置呢？3. 下图是课室座位的平面图，你能根据以下座位找到对应的同学参加数学问题讨论吗？（先横后竖）

这种问题情境的创设能让学生感受到数学来源于生活，从而更喜欢数学。荷兰教育家弗赖登塔尔认为：“数学来源于现实，存在于现实，并且应用于现实，数学过程应该是帮助学生把现实问题转化为数学问题的过程。”因此，教师有必要在数学课上结合现实生活传授知识，以吸引学生学习数学知识和激发学生思考数学问题的兴趣。

三、精选巧设练习，提高学生的思考能力

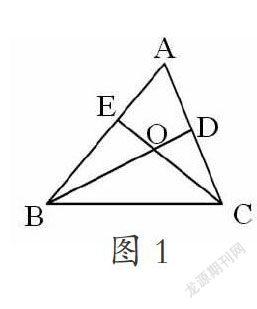
练习题组的选择和设计要以学生的认知为基础，由易到难、循序渐进进行选择设计。学生通过练习，可以感受到知识的关联性，在思考问题的过程中培养学生求同存异的思维能力以及培养学生思维的敏捷性。练习题组设计有递进、有变化、有对比，更能有效地培养学生自主思考的能力，有助于提高学生的思维的灵活性。比如《三角形》的章节复习：如图1，在△ABC中，∠ABC、∠ACB的平分线BD、CE交于点O。

变式1：若∠A=80°，则∠BOC=   。（130°）

变式2：你能猜想出∠BOC与∠A之间的数量关系吗？（∠BOC=90°+∠A）

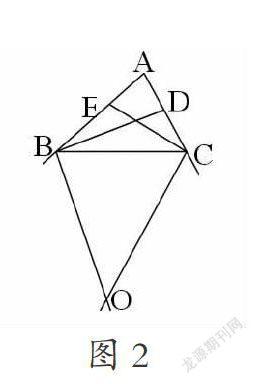
变式3：如图2，若换成两外角平分线相交于O，则∠BOC与∠A又有怎样的数量关系？（∠BOC=90°-∠A）

该题型主要考查学生运用三角形的内角和定理以及角平分线的性质进行推导。该题组呈梯度变化，由浅入深，容易使学生逐步适应、有条理地理清思路。这样的练习题组设计在潜移默化中渗透了数学思想方法的培养，让学生在不知不觉的思考中提高了思维能力以及概括能力。

除上述几方面以外，数学教师也要针对学生个体的差异，在教学过程中及时做好学习反馈工作，调整教学策略。教育家苏霍姆林斯基说过：“在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者，而在儿童的精神世界中这种需要特别强烈。”因此，教师在数学课堂教学中要懂得放手，适时创新教学模式，为学生创设广阔的思维空间，引导学生自主探索思考，使学生的创新性思维得到发展，为培养创新型人才夯实基础。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]朱智贤，林崇德.思维发展心理学[M].北京：北京师范大学出版社，1986.

[3]李玉琪.中学数学教学与实践研究[M].广州：高等教育出版社，2001.

[4]徐斌艳.数学教育展望[M].上海：华东师范大学出版社，2001.