钣金件中匹配孔的半径差及轴线重合度自动检查

刘 福，董玉德，王 亮，宋 健，吴海江，邹文俊，霍美玲

钣金件中匹配孔的半径差及轴线重合度自动检查

刘 福1，董玉德1，王 亮1，宋 健1，吴海江2，邹文俊2，霍美玲2

(1. 合肥工业大学机械工程学院，安徽 合肥 230009；2. 上海翼锐汽车科技有限公司，上海 201805)

针对汽车钣金件中匹配孔的半径差及轴线重合度人工检查效率低、易遗漏等问题，提出了钣金件中匹配孔的半径差及轴线重合度自动检查方法。首先将获得的B-Rep三维模型以面壳封闭的方法拓扑分解为面基本单元；其次根据圆柱面具有2条半圆弧线和2条直线的特征对圆柱面进行筛选，并以其为基本单元对圆孔和槽孔进行提取；然后分别获取圆孔和槽孔的半径及轴线，并利用点到点和点到线距离方法，根据孔匹配原理对匹配孔进行检查分析；最后对半径差不满足要求和轴线不重合的孔对进行标注。借助CATIA的CAA开发平台对相关算法进行了系统设计，并验证方法的可行性。实例检查结果表明，该方法能够高效、准确的对钣金件中匹配孔的半径差及轴线重合度自动检查。

匹配孔；B-Rep三维模型；圆柱面；半径差；轴线重合度

传统的汽车研发制造是一个串行过程，设计师与工程技术人员之间未形成真正高效的交流与互动，该研发制造流程造成了效率低、成本高等问题。为解决这些问题，现代汽车研发采用了一种基于可制造性设计(design for manufacturability, DFM)的并行工程[1-3]，对匹配孔的半径差与轴线重合度进行检查，是并行工程中的一项重要内容。当匹配孔半径差过大或过小及轴线不重合时，会存在功能孔被遮挡、定位失败及零件错位等危害，导致后续制造及整车装配出现问题，影响整车配合性能[4]。为实现匹配孔的半径差及轴线重合度自动检查，需要对孔进行有效地识别和提取。

文献[5]利用侦测多面虚拟迴圈，并藉此辨识三维模型中的凹陷与突起特征，从而识别面上的圆，不能对孔深进行判断。文献[6]通过对IGES文件中裁剪参数曲面实体的曲面内边界进行内轮廓特征识别，并提取圆孔，要求模型具有数据参数。文献[7]采用孔系功能语义的特征识别方法，通过与计算机存储孔系特征进行对比提取孔。文献[8]在双目立方体视觉测量原理的技术上，以激光器辅助扫描被测孔槽完成三维测量，该方法是一种在线测量方法，可对实体进行检测。文献[9]中的孔特征提取是利用Solid Edge同步建模技术进行识别，且只能进行圆孔的直径大小修改，未对其他类型的孔进行提取。曾俊皓等[10]通过选择钣金零件的基准面对钣金件的单元特征进行识别，并与特征类库进行匹配判断完成孔的提取。

汽车装配体钣金件中都会有一些特殊功能的圆孔和槽孔，如进行人工检查会造成耗时长、孔遗漏等问题。此外，现有的三维模型设计软件种类较多，会造成零件的格式多种多样，有带设计参数的数据文件，也有不带任何设计参数且只有实体的中间格式文件。如何找到一种基本通用算法对所需的圆孔与槽孔的半径与轴线进行提取是目前所要解决的问题。为此本文提出了一种钣金件中匹配孔半径差及轴线重合度自动检查方法。

1 方法概述

钣金件是由金属薄板综合剪、冲/切/复合、折、铆接、成型等冷加工工艺加工而成的同一种零件且相同厚度的产品。匹配孔就是由2贴合钣金件中各个孔匹配形成，既有相关的配合关系，又有一定的定位关系，如图1所示。在众多钣金件模型中找出所有匹配孔并判断是否合格，给可制造性分析人员带来极大的不便。目前，钣金零件设计软件很多，如Pro/E、Solid-Works、CATIA等，其生成的文件格式各不相同，如何找到一种通用的方法来提取钣金件中的匹配孔并进行判断，是钣金件分析中的一个问题。本文所提出的匹配孔中半径差及轴线重合度自动检查方法能够对无参数模型中的圆孔与槽孔进行提取，并获得孔的半径与轴线。无论数据模型有无设计参数，只要能将模型实体分解成点线面信息，就能对圆孔与槽孔进行提取并获得其半径与轴线。

图1 匹配孔

匹配孔的分析过程为圆柱面筛选、孔的提取匹配以及分析应用3个过程，如图2所示。首先将边界表示法(boundary representation, B-Rep)的三维模型拓扑分解为面基本单元，根据面积阈值筛选出一定大小的面；再以面的边线为研究对象，根据圆柱面的几何特征筛选出圆柱面，并以其为基础确定圆孔和槽孔。最后对各零件的孔利用点到点和点到线的距离进行匹配判断。分析应用是对半径差不符合要求时对2个孔的半径和孔轴线不重合时的轴距进行标注，并记录2个匹配孔的零件信息，使可制造性分析人员对不合格的匹配孔对有直观的了解。

图2 结构体系框架

2 孔特征提取

B-Rep[11]和体素构造法(constructive solid geometry, CSG)[12]是2种表达CAD模型的主要方式。其中，CSG多用于造型，而B-Rep是几何造型中最成熟、无二义的表示法，也是目前最为常用的几何模型表达形式，并且在CAD模型的分析、比较以及处理上更具优势。现有主流商用CAD系统大都提供了将自身格式的设计文件转换成边界表达模型的功能[13]。计算机中常用的三维形体欧氏5层拓扑结构为点、边、环、面和体[14]。根据文献[15]对B-Rep模型基于封闭面壳的分解方法，可将三维模型分解为点、线、面等特征，从而获得所有面基本单元。对所有面进行判断，可以对孔特征进行提取，分析流程如图3所示。

2.1 孔圆柱面提取

面包括平面和曲面等，是大多数孔面特征的重要组成部分。对圆柱面进行提取筛选，需要将三维模型分解为面特征，这样针对各种格式的三维模型数据都能进行有效的处理。在分解三维模型时，会产生一些不符合要求的面，其面积较大，不符合形成孔面的条件，需根据具体的模型尺寸进行相应的面积阈值调整。本文针对汽车钣金件的孔进行研究，根据钣金件的厚度特点和汽车钣金零件上形成匹配孔的半径一般不超过15 mm，所以将筛选面积最大阈值初步定为300 mm2。分解后的面中存在很多大小不一的孔洞，如图4所示，当面的边数远远大于6条，直接剔除。同样有一些比较特殊的面，其边数小于4条，因不能满足形成圆柱面条件，也直接剔除。由于有的圆柱面中存在噪点，且多出现在圆弧边上，如图5所示，所以形成圆柱面的边线也可能有5条或6条，因此边数条件设置为4~6条。

图3 孔提取流程图

图4 多孔面

进行圆柱面判断时，分为2种情况：

(1) 当面的边数为4条时，需对4条边分别进行判断。获取线的2个端点与中点1，2，3，由点1和2形成直线(,,)，若3在直线上，则该线为直线；若不在上，计算2个端点的中点12，利用相交弦定理式(1)得到式(2)，计算出假定半径，当=112=123时，则该条线为半圆弧。若该面存在半径相等的2条半圆弧线和2条直线，则判断为圆柱面，即

图5 5条边圆柱面

(2) 当面的边数大于4小于等于6时，其中任意2条曲线中第(=1,2)条线段的表达式为

2.2 圆孔和槽孔提取

2.2.1 圆孔提取

获得圆柱面后，要对其中任意的2个面进行圆孔判断。首先获得圆柱面的上下2个圆弧线圆心点，求出2个圆心点的中点即为圆柱面中心点，对2个圆柱面的中心点进行判断，若中心点重合，则说明2个圆柱面组成一个圆孔。

2.2.2 槽孔提取

槽孔可看作由4个面片组成，2个柱面分别被2个平面连接。判断任意2个圆柱面的中心点距离，若在一定范围内(该范围根据具体三维模型的大小和孔的特征来定)，则利用三维物体的准最小包围盒快速求解方法[16]，分别求出2个圆柱面的最小包围盒，综合求出2个圆柱面包涵在内的包围盒1。

对平面求包围盒2，当1与2相交时，获得平面边线，判断平面中是否有2条边线分别与2个圆柱面的直线边重合，若重合，则2个圆柱面由该平面连接。当存在2个平面时，这4个面片组成一个槽孔。

3 匹配孔分析

3.1 孔匹配计算

产品在设计时，有时缺乏整体的装配信息，也未考虑装配体中零件之间的关联、约束和定位关系，所以零件本身的坐标系在装配体中是独立的，不与装配体坐标系重合。在各零件中所获得的各点坐标信息只是零件的相对坐标系中的数值，在进行孔匹配时是利用点到点与点到线的距离来进行判断，所以要获得零件在装配体中的位姿转换矩阵，将获得的各点坐标值转换为绝对坐标系中的数值再进行孔匹配检查。

零件的转换矩阵=()，其中，为旋转变换矩阵，为平移量，圆孔的相对坐标值(,,)利用式(3)转换为绝对坐标数值(X,Y,Z)。其中

3.1.1 圆孔匹配

圆孔上下圆弧圆心点的连线既为孔的轴线，圆孔中心点为P1(X1,Y1,Z1)，另一零件中圆孔的中心点为P2(X2,Y2,Z2)，利用式(4)和式(5)求点P2到孔轴线的垂足，并计算P1与垂足的距离1，P2与垂足距离为2。2个圆孔高度分别为1和2，当满足|(1+2)/2–1|<=0.5，可根据匹配孔定义调整值，且2<3(数值可调)，则判断2孔匹配。

4点坐标值为：(1,1,1),(2,2,2),(0,0,0),(x,y,z)。

点为点到直线的垂足，则

3.1.2 槽孔匹配

槽孔具有2个轴线，若要进行匹配首先要拟合出一条轴线，由槽孔的2个柱面上下圆弧圆心点进行拟合，各点为P1、P1、P2、P2。分别计算P1与P2和P2的距离3和4，若3>4，则交换P2与P2的值，拟合轴线上2个点分别为1=(P1+ P2)/2和2=(P1+P2)/2，孔中心点为P=(1+2)/2。拟合后，根据圆孔匹配方法进行匹配。

3.2 孔半径差及轴线重合度分析

分析圆孔与槽孔半径差，只需分别计算2个匹配孔中的圆柱面圆弧圆心和圆弧线上一点的距离，记为1和2，若满足≤|1–2|≤，则为半径差设计合格的匹配孔，其中和为人为设定检查标准。

圆孔轴线重合度检查，只需对圆孔匹配时距离1进行判断，若1等于零，则判断为轴线重合。

分析槽孔轴线重合度，要对孔的2个轴线进行重合度分析。其中一个孔的2条轴线分别为11与12，其上2个点分别为P11，P11和P12，P12。另一个孔的2条轴线分别为21与22，其上2个点分别为P21，P21和P22，P22。分别计算出P11与P21，P22的距离5，6，若5>6，则P21与P22，P21与P22交换数值。此时计算P21到轴线11的距离7，P22到轴线12的距离8，当7和8都等于零时，判断为轴线重合。

4 实例分析应用

为验证本文提出的汽车钣金件中匹配孔的半径差与轴线重合度自动检查方法的可行性和准确性，以CAA为开发平台借助Visual Studio2008工具对CATIA进行二次开发并嵌入其中。实例分析操作界面如图6所示，其中图6(a)为主操作对话框，图6(b)为点击复选按钮弹出的复选框。首先输入检查标准，然后选择编号为123456789零件总成为检查零件，点击确定按钮对零件进行检查。图7为实例分析模型前后对比，图8为分析模型局部放大图。本模型共分析了27个零件，72个孔，用时6.43 s。

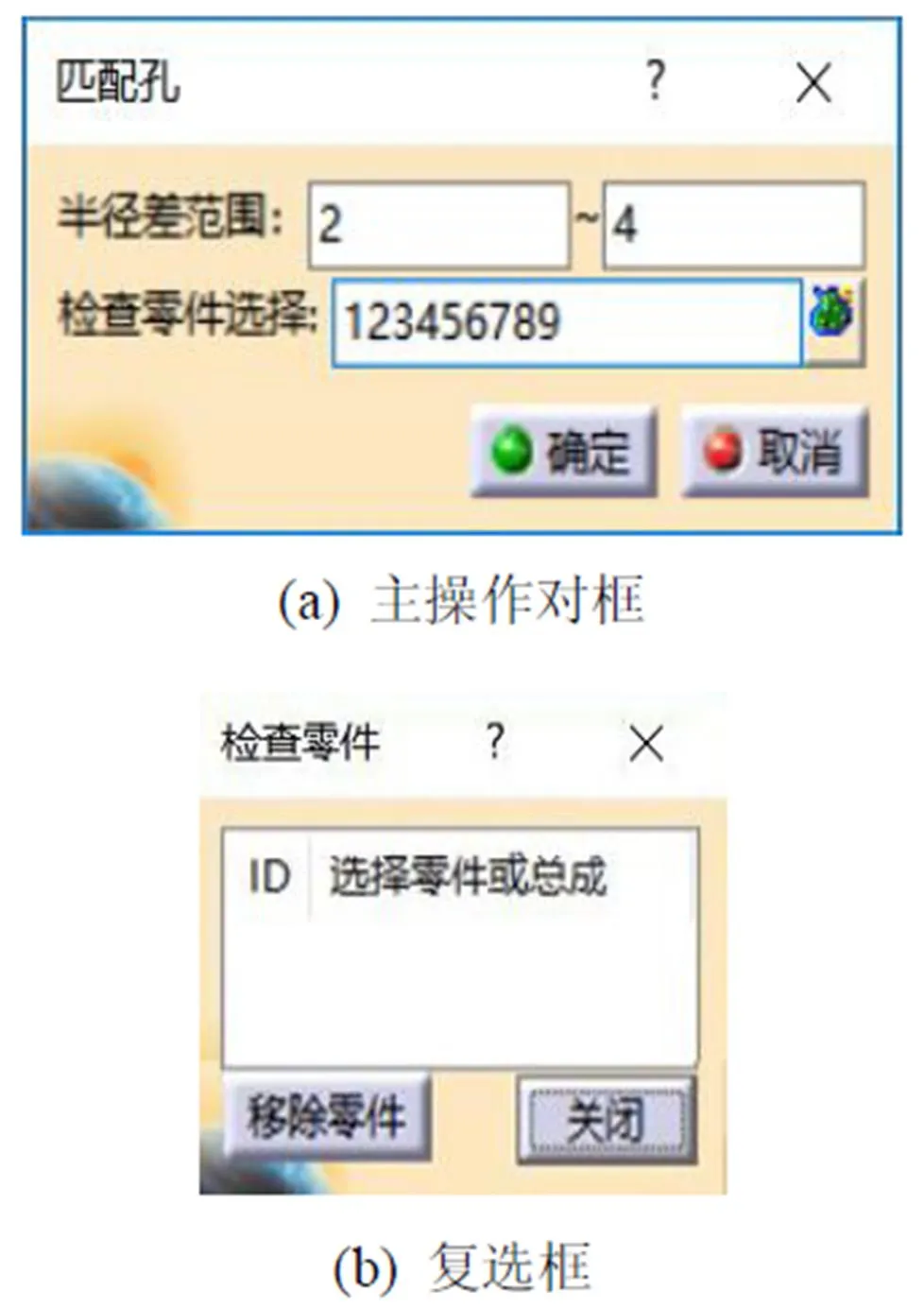
图6 操作界面

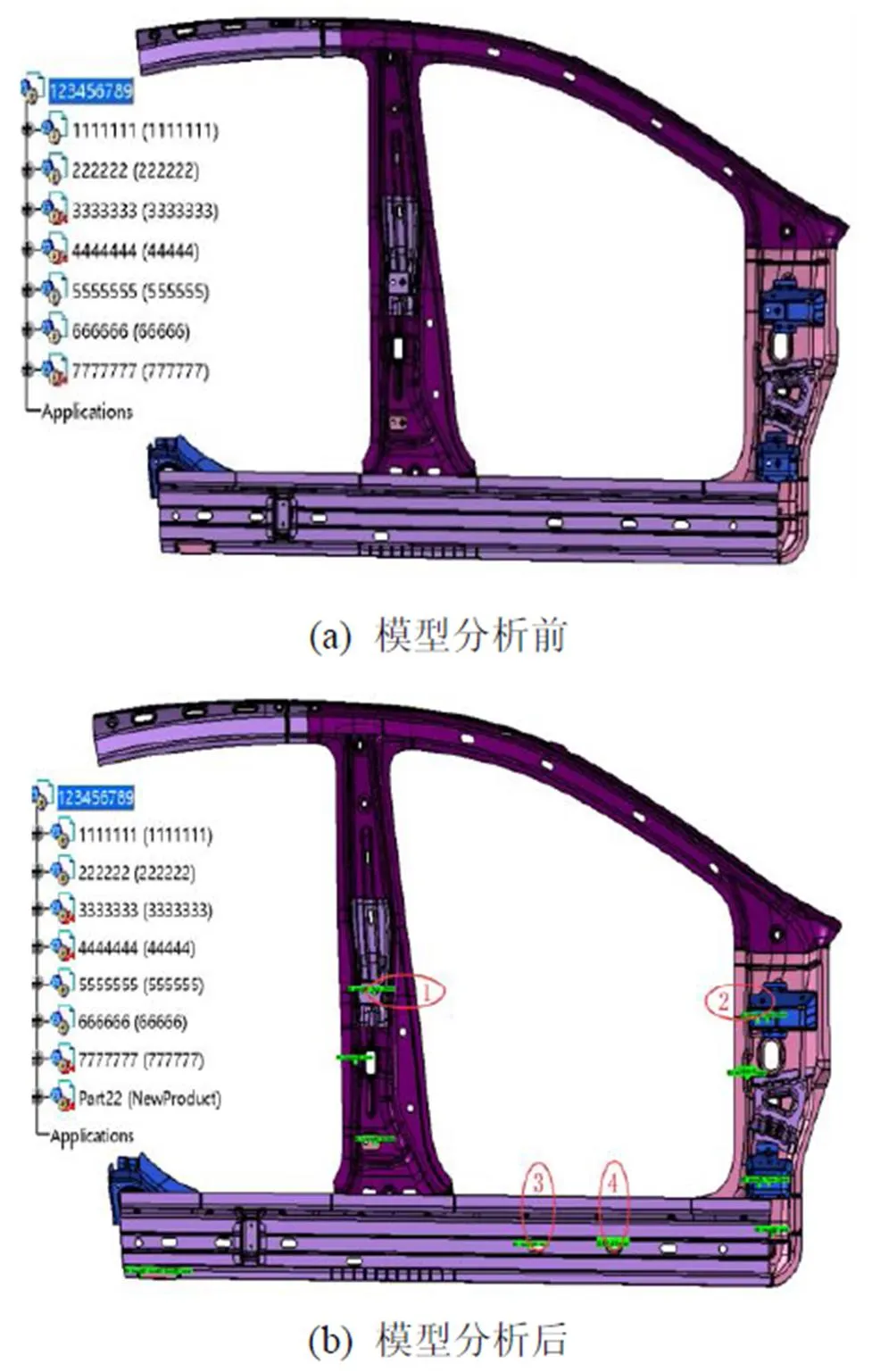
(b) 模型分析后

(a) 标识1个圆 孔半径差(b) 标识2个圆孔 轴线重合度 (c) 标识3个槽 孔半径差(d) 标识4个槽孔 轴线重合度

5 结 论

本文针对现代汽车可制造性分析过程中出现的人工手动检查效率低下、易遗漏等问题，提出了钣金件中匹配孔的半径差及轴线重合度自动检查方法，使得匹配孔检查在保证准确性的前提下极大地提高了检查效率。本方法能够对无参数模型实体进行拓扑分解后，对圆孔与槽孔的半径与轴线进行提取。但对孔特征的提取前提条件是实体能够进行分解，对于如何筛选出其他的特征孔，如方孔、椭圆孔等，还未进行研究，其限制了孔的全面筛选，也不能对三维模型中所有的孔进行分析。后续将以此为研究方向，从而为孔特征的提取、及可制造性分析提供参考。

[1] 李能文, 陈东, 耿富荣, 等. 并行工程下面向制造的车用复合材料产品设计体系模型[J]. 汽车工艺师, 2018(8): 57-60.

[2] 袁立, 谭红毅, 王桂楠, 等. 并行工程与敏捷研制管理在飞机研制中的应用[J]. 航空制造技术, 2014(3): 26-29.

[3] 阮露. 并行设计思想在专用车公司中的应用研究[J]. 汽车实用技术, 2018(12): 93-94.

[4] 庞禄. 白车身车门装配质量分析与控制[D]. 天津: 天津大学, 2015.

[5] LAI J Y, WANG M H, CHIU Y K, et al. Recognition of depression and protrusion features on B-rep models based on virtual loops [J]. Computer-Aided Design and Applications, 2016, 13(1): 95-107.

[6] 许加陈, 游有鹏. 基于IGES的钣金零件特征识别的方法研究[J]. 机电工程, 2017, 34(6): 582-585, 602.

[7] 卢远志, 钟志华, 文桂林. 模具零件工程图的孔特征识别与分组统计[J]. 湖南大学学报:自然科学版, 2010, 37(2): 22-26.

[8] 胡彦强, 马钺, 许敏. 白车身孔槽类特征三维坐标在线测量方法研究[J]. 计算机工程, 2017, 43(10): 186-191, 97.

[9] 曾俊皓. Solid Edge同步建模技术在孔特征及孔阵列识别中的应用[J]. 数字技术与应用, 2017(5): 71-73.

[10] 刘志坚, 王义林, 李建军, 等. 钣金零件特征识别方法的研究[J]. 中国机械工程, 2002, 13(24): 2115-2118.

[11] 马善坤, 刘长安, 方文涛. 基于加工特征的B-rep模型几何变换算法[J]. 组合机床与自动化加工技术, 2012(4): 20-24.

[12] DU T, INALA J P, PU Y W, et al. InverseCSG [J]. ACM Transactions on Graphics, 2019, 37(6): 213: 1-213: 16.

[13] 龚雄, 赵建军, 王启富, 等. 边界表达模型的局部几何更新方法[J]. 机械科学与技术, 2007, 26(1): 92-95.

[14] 王慧奇. 特征造型中拓扑元素命名及辨识方法研究[D]. 大连: 大连理工大学, 2009.

[15] 罗月童, 樊晓菁, 俞盛朋, 等. 基于面壳封闭的B-Rep至CSG转换算法[J]. 计算机辅助设计与图形学学报, 2014, 26(10): 1673-1680.

[16] 尹逊刚, 孙殿柱, 李延瑞, 等. 三维物体的准最小包围盒快速求解方法[J]. 组合机床与自动化加工技术, 2017(7): 51-54.

Automatic Inspection of the Radius Difference and Axis Coincidence of Matching Holes in Sheet Metal Parts

LIUFu1, DONGYu-de1, WANGLiang1, SONGJian1, WUHai-jiang2, ZOUWen-jun2, HUOMei-ling2

(1. School of Mechanical Engineering, Hefei University of Technology, Hefei Anhui 230009, China; 2. Shanghai Yirui Automobile Technology Co. Ltd, Shanghai 201805, China)

Aiming at the problems of low precision and easy omission of the matching hole’s radius difference and the axis coincidence ratio in the automobile sheet metal parts, the automatic inspection method of the radius difference and the axis coincidence degree of the matching holes in the sheet metal parts is proposed. Firstly, the obtained B-Rep three-dimensional model is topologically decomposed into the basic unit of the face by the method of the closing shell. Secondly, according to the characteristics of two semicircular arc lines and two straight lines on the cylindrical surface, the cylindrical surface is screened, and the circular holes and slots are extracted by using the cylindrical surface. Then the radius and axis of the circular hole and the slot are obtained respectively, and the point-to-point and point-to-line distance method is used to check and analyze the matching hole according to the hole matching principle. Finally, the hole pairs whose radius difference does not meet the requirements and the axes do not coincide is marked. The system design of related algorithms is carried out by using CAA development platform of CATIA, and the feasibility of the method was verified. The example inspection results show that the method can automatically and accurately check the radius difference and the axis coincidence ratio of the matching holes in the sheet metal parts.

matching holes; B-Rep three-dimensional model; cylindrical surface; radius difference; axis coincidence ratio

TP 391

10.11996/JG.j.2095-302X.2019040790

A

2095-302X(2019)04-0790-06

2019-03-13；

定稿日期：2019-04-08

国家自然科学基金项目(51775159)

刘 福(1993-)，男，安徽阜阳人，硕士研究生。主要研究方向为计算机辅助机械产品设计与分析。E-mail：940512716@qq.com

董玉德(1966-)，男，安徽合肥人，教授，博士，博士生导师。主要研究方向为计算机辅助设计(CAD/CAE/PDM)。E-mail：dydjiaoshou@126.com