面向球幕投影系统的几何校正方法

王明冬，盖 孟，赖舜男，王 震

面向球幕投影系统的几何校正方法

王明冬1，盖 孟2,3，赖舜男2,3，王 震4

(1. 北京大学深圳研究生院信息工程学院，广东 深圳 518055；2.北京大学信息科学技术学院，北京 100871；3. 北京大学北京市虚拟仿真与可视化工程技术研究中心，北京 100871；4. 沈阳理工大学，辽宁 沈阳 110159)

用于飞行模拟的视景仿真系统，经常会以多台投影仪同步投影以得到较大范围的视场角。当投影机斜对屏幕或者投影屏幕为曲面时，图像会发生几何失真。针对此问题，本文提出了一种专门面向球幕投影系统的几何校正方法，并以一个三通道显示系统为实例，详述了该方法的理论原理以及校正流程。实例结果表明，经几何校正后，各投影图像无几何畸变，通道过渡处几何内容完全一致。该方法是一种纯软件方法，成本小而且操作简单，能够适应于不同的投影场景。

球幕；几何校正；飞行模拟器；多投影；OpenGL

随着计算机显卡绘制功能的快速发展，飞行模拟产业也开始蓬勃发展，视觉模拟作为飞行模拟器的所有模拟环节中最贴近飞行员感官的一环，也越来越受到行业内的重视，在整个系统研发中所占据的比重也越来越大。

为了弥补单个投影机视场角不足的限制，一般都会利用多台投影仪进行联合同步投影[1-2]，将投影图像进行拼接，在逻辑上可形成一个全景图。投影屏幕的形状多以柱面和球面常见，具有光路设计简单、成本适中、视场角宽阔等优点，在战斗机、直升机等飞行模拟器中经常用到[3-7]。相对于柱面、球面在垂直视场方向能够带给人更平滑的视觉过渡，因此，在垂直视场角较大的情况下，一般都会选择球形的投影平面。

一般的投影机都带有梯形校正功能，可以校正因为投影机斜对屏幕导致的透视形变。但当屏幕是曲面时，大多数投影机都无法正确处理，此时就需要使用其他方法对投影画面进行几何校正[8]。

目前，软件几何校正方法主要有RASKAR等[9]提出的矩阵映射方法，及多项式函数校正方法[10]等，其均通过相机采集反馈图像，并在二维平面内进行矩阵映射或多项式插值计算实现几何校正，使用不够灵活方便，计算量相对较大。

鉴于上述情况，本文以某飞行模拟器视景仿真系统为实例，提出了一种针对球形投影幕的软件几何校正方法，并详细描述了其流程和原理。该方法不需要增加额外的硬件设备，成本低、粒度小，可以作为视景系统的一个内部子系统进行嵌入且不影响绘制效率。同时，该方法可扩展性高，对于规则二次曲面，可通过细微的改动达到校正的效果。

图1为实例系统的整体架构，系统包括了一个主系统和多个从系统(图中只展示了2个)。通信子系统负责与主控对接，将主控传来的信号翻译并发送给多机同步子系统，多机同步子系统负责各个通道之间的绘制同步，在每帧开始时，分发来自通信子系统的绘制信号，结束时，发送图像刷新指令，所有机器同时将图像送往投影机进行投影[11]。曲面校正子系统负责对绘制子系统生成的图像进行扭曲处理，该扭曲处理使得图像经过投影仪投射到球面上刚好形成正常透视的图像。融合子系统负责对各个投影机投影的重合部分的亮度进行由明到暗的过渡处理，使整个视景在融合区域平滑过渡。

图1 视景系统整体架构[12]

曲面校正方法的流程如下：

(1) 给投影平面建立参数化表达，并以参数为度量，划分每台投影仪的投影范围及融合区域。

(2) 利用交互式程序，对输入图像和球面上投影点的映射关系进行拟合。

(3) 针对每台投影仪的投影范围，计算对应视景通道的视锥参数。

(4) 确定曲面校正子系统中的扭曲处理算法。

1 投影区域的参数化表达

在计算机上存储一个球面是相当困难的，若将球面离散成一些小片也是相当复杂的。因此，在计算机图形学领域，一般采用球面经纬映射图像的方法描述一个球面，也就是将球面上的点按照经纬度映射到一个矩形纹理上，经度()映射成矩阵的水平坐标，纬度()映射成垂直坐标。但是该映射会产生水平方向的拉伸问题，赤道上的比例是正常的，越靠近两极，拉伸越严重，在极点处一个点变成了一条线。在大多数情况下，经纬度映射还是相当好用的。

事实上，常见的矩形地图就是经纬度映射图像。当映射整个球面时，由于球面的经度范围比纬度范围多一倍，将得到一个长宽比为2∶1的矩阵。图2展示了球面上的点和在经纬映射平面上对应点的关系。

在实例系统中，投影平面是一个半径为3 m，经度跨幅约230°，纬度范围从约–30°~+30°的球带。由3台投影仪排成一行进行投影，中间的投影通道为主视景系统，两侧为从视景系统。飞行员的眼点位置处于球心处。以飞行员眼点位置为原点，右手方向为轴正方向，竖直向上为轴正方向建立飞行员观察坐标系eye–。不失一般性，记球心在观察坐标系下的坐标为(center,center,center)，显然，飞行员眼点不可能出现在球外，因此必然有

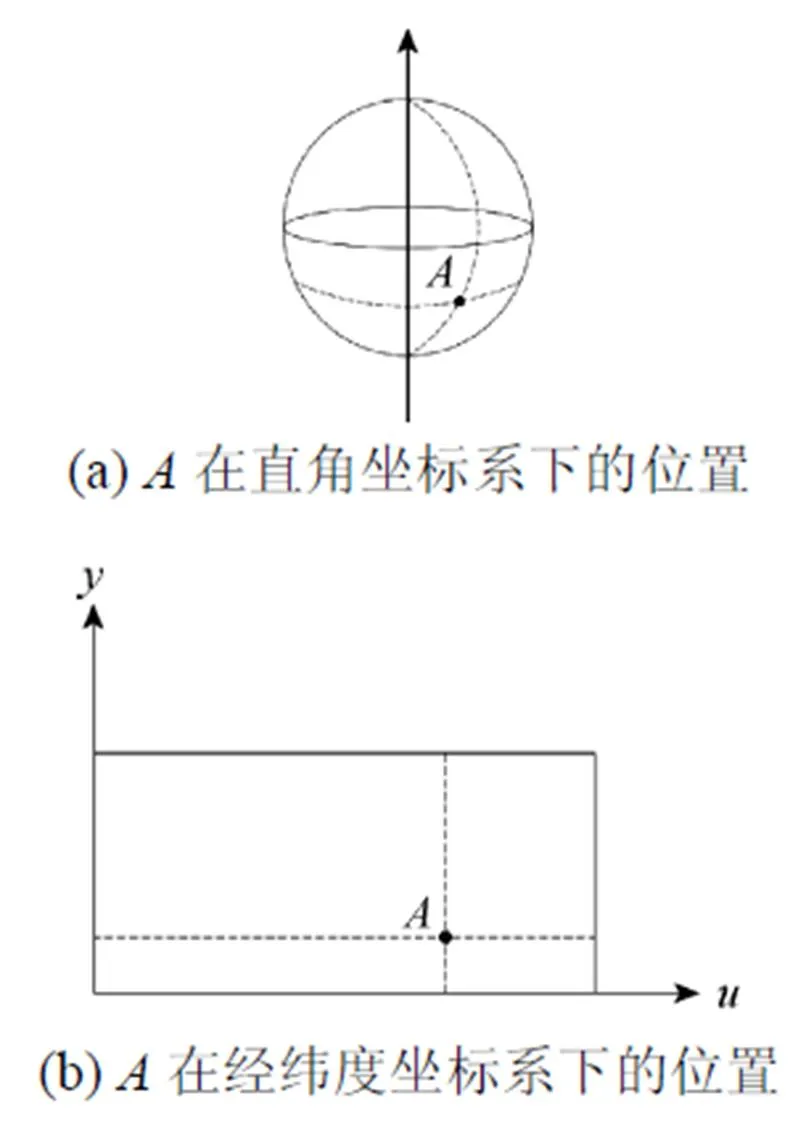
图2 经纬度映射示意图

参考观察坐标系，建立球面的经纬度坐标，球面上点到观察坐标系的变换关系为

依据每台投影仪的投影范围上限，将其裁减为经纬度坐标系下的矩形。裁剪后，3台投影仪投影纬度范围为–30°~30°，从右向左3台投影仪投影的经度范围依次为[–115°, –35°]、[–50°, 50°]、[33°, 113°] (投影仪自右向左，投影范围自左向右)。

2 投影仪投射关系的拟合

为找到并记录输入图像到投影曲面之间的映射关系，使用参考文献[13]的方法，用贝塞尔曲面拟合其逆映射，即为投影曲面到输入图像的变换关系[13]。

×次的二维贝塞尔曲面的表达形式为[14]

其中，K,j为曲面的控制点；B,m()和B,n()是混合函数伯恩斯坦多项式，即

将(,)当作投影曲面参数归一化后的坐标，(,)当作输入图像的坐标，式构成了从投影曲面向输入图像空间的映射。

需寻找到(+1)×(+1)个控制点，使得由此生成的贝塞尔曲面与投影曲面基本吻合即可。实践表明，在大多数情况下，对于球面投影拼屏幕，取4×4阶贝塞尔曲面就能够得到较佳的结果>[13]。利用交互式程序可完成该过程：

(1) 将球面参数和归一化到[0,1]范围，变为和。随后对和分别进行和等分，加上端点总共能够得到(+1)×(+1)个不重复的目标点(u,v)(0≤≤,0≤≤)。

(2) 利用交互式程序调整上一步得到的关键点坐标对应的(u,v)的位置，使得(u,v)正好投射在参数(u,v)所对应的球面位置，同时利用式实时反解K,j的值，重构整个曲面；此时发现，生成的曲面已经与投影幕的参数曲面足够吻合。

图3为实例系统的中间通道的拟合结果以及两边通道的部分结果，颜色较深的部分为重合区域。取4×4阶贝塞尔曲面，每台投影机输出的曲面60等分，第0，15，30，45，60个等分格处为选中的用来重构曲面的关键点。图4为中间通道的贝塞尔曲面在输入图像空间的呈现。至此，已经得到了表示投影曲面到输入图像之间变换关系的贝塞尔曲面，只需简单地用(,)作为顶点位置，(,)作为输出数据，创建且光栅化贝塞尔曲面的细分网格，得到的图像记录了从输入图像到投影曲面的映射关系。

图3 拟合结果

图4 中间曲面在图像空间的展示

3 视锥参数的计算

计算各个通道的视锥参数，使视景的绘制子系统利用此视锥参数以及多机同步子系统发送的相关参数，计算观察矩阵以及透视投影矩阵，进行场景的绘制。

若某个通道的投影范围为[,]× [,]，要计算视锥参数，需要首先确定摄像机观察坐标系O–。

在OpenGL中，一般用摄像机位置、上方向以及观察方向3个向量来确定观察坐标系，并依次考虑其设置。除特殊情况，均应该将摄像机位置与飞行员观察坐标系原点重合。任何经过摄像机的直线，在飞行员眼中均可投影成一个点。对于图像的像素点，在进行几何校正时，可不考虑该点的深度信息，因为其深度不会影响人眼中的成像位置。

在实例系统中，这种纬度范围离两极球带较远，可以简单地让上方向和飞行员观察坐标系的轴重合。其好处是做透视投影时，经度线会投射成一条平行于轴的直线，计算视锥时会较方便。

接下来需考虑观察方向的设置，观察方向是垂直于上方向的，因此必然是水平的。生活中人们知道，正视一个物体时，看的最清晰。因此，想要得到一个好的透视投影效果，观察方向应该垂直于观察平面，但是对于球面，很难定义其垂线方向。一般情况，可将其设置为一个变量，定义域为从观察坐标系原点出发，所有与投影范围相交射线的方向。用户通过调节其值，得到最好的投影效果。

实际上，对于某些在垂直视场方向要求比较高，甚至投影区域包含了北极点的情况，几何校正系统可规定摄像机观察坐标系的原点，上向量和观察向量均作为参数，交给用户去调节。考虑到摄像机观察坐标系原点和飞行员眼点是重合的，而且同是右手空间直角坐标系，可用欧拉角中的和作为参数，用户可对其进行调节。摄像机观察坐标系是通过飞行员观察坐标系做相应的欧拉旋转实现的。记飞行员观察坐标系到摄像机观察坐标系的变换矩阵为，则坐标变换关系为

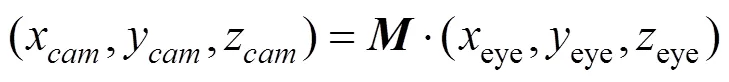
对于实例系统，因为飞行员眼点处于球心，可简单的将飞行员观察坐标系绕沿自身轴顺时针旋转(+)/2.0，变为该通道的新的观察坐标系。

从两方面考虑视锥的设置：①为了保证投影区域内的颜色均有意义，该通道在球幕上的投影范围必须都在视锥的裁剪范围之内；②对于无效像素点的绘制，会造成计算机资源的浪费。理想情况下，该通道的视锥和球幕投影区域在近裁剪面上的投影应该是重合的，但实际上，经纬度参数下的矩形区域投射到空间直角坐标系，并不会是一个矩形，所以二者不可能完全重合。只能选取球幕在近裁面的投射区域的外接矩形，作为视锥范围。可以通过式和式将球面的经纬度坐标点变换为摄像机坐标系，将定义域限定为投影范围，求出对应值域的范围即得到了视锥范围。

图5为正前方半球的经纬网在近裁剪平面上的透视投影，可以很清晰地看出，在近平面上，经线会投射成一条平行于轴的直线，纬线中赤道会投影为一条平行于轴的直线，其余的纬线中心向赤道凹曲。

图5 经纬网的透视投影

在OpenGL中，一般会用，，，，，6个参数来确定透视投影矩阵。其中，和为近裁剪面和远裁剪面与视点的距离，，，，为视锥在近裁剪平面上的投影。由6个参数，确定了视锥的6个裁剪平面，相对于几何校正而言，只需要关注左右下上4个裁剪平面即可，而期只和，，，与的比值有关，因此只需要计算该4个比值即可。可将4个比值记为，，，，即

根据和的正负性，简单的分为3种情况：

(1) 当0≤<时

(2) 当<0≤时

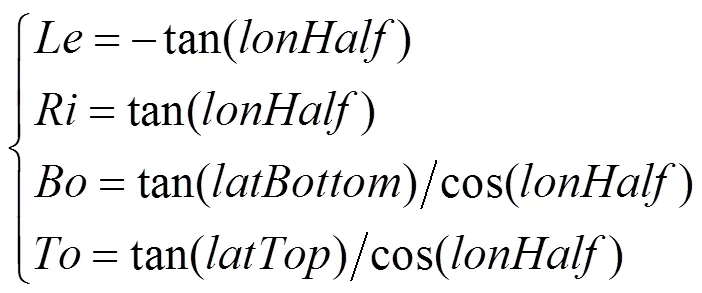
(3) 当<<0时

4 扭曲处理算法

对绘制子系统生成的图像进行扭曲处理，使其经过摄影仪投射到球幕上，显示出正确的结果。

如图6所示，为球幕上的一个点，投影仪会将输入图像的点投影到处，而在正常情况下，飞行员在点看到的应该是近裁剪平面上点的图像。因此，只需将近裁剪平面上点的像素颜色赋于输入图像所在的位置。这样，经投影仪投影后，飞行员即可在点看到正确的结果。

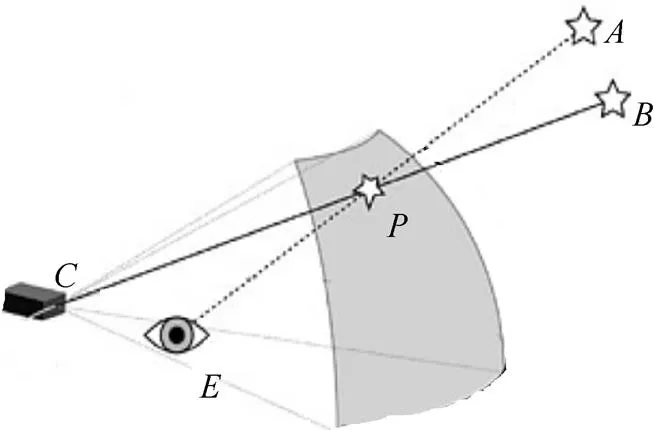
图6 扭曲处理示意图

对于输出图像的每一个像素，通过在第2节拟合的投影仪映射关系，很容易判断出该像素是否会被投射到限定的投影区域。若否，直接将该点的亮度设为0，继续处理下一个像素，反之，能够获得投影点的归一化参数坐标值，对其进行归一化的逆操作，便得到该点在球幕的投影点的经纬度坐标(,)。利用式和式，将其变换到观察坐标系，再通过第3节得到的透视投影矩阵以及齐次变换，即可得到应该被扭曲到点的像素点的纹理坐标。

对于实例系统，将视锥参数，代入式，便可得到

将输出图像由投影仪进行投影，即可得到正确的图案。图7为不做几何校正前的视景图像，图8和图9为校正后的视景图像。

图7和图8是相同视角下的2张图，通过对比，可以发现图7中，2台投影仪的过渡处几何内容未完全匹配；图8则没有这种现象。图9在整体上对几何校正的结果进行了一次展示，可以看出，3个通道的视景图像均已解决了几何畸变的问题，在相邻通道的过渡处，图片的几何内容完全重合。

图8 几何校正后的视景1

图9 几何校正后的视景2

5 结束语

本文针对面向球形投影幕的飞行模拟器视景仿真系统，提出了一种简单、灵活、高效的软件几何校正方法。对比其他的软件几何校正方法[8-10]，有以下主要优点：

(1) 校正无需相机的采集反馈，工作量小。本文所述的几何校正方法只需一次校正预处理，无需相机的图像采集反馈就能实现几何校正。对比于矩阵映射以及多项式插值的校正算法，计算复杂度可以忽略不计，实时性高。

(2) 校正方法灵活，适用性强。该几何校正方法不关注投影仪是否正投，且只需简单地改变投影幕参数化表达方法，就可以适用于其他的二次规则曲面，适用性强、易于推广。

[1] FERREIRA F T, KURASHIMA C, CABRAL M C, et al. A small-scale and flexible platform for multi-projector systems development [C]//2013 XV Symposium on Virtual and Augmented Reality. New York: IEEE Press, 2013: 216-219.

[2] SONG Z J, GONG G H, HUANG Z P, et al. A new edge blending paradigm for multi-projector tiled display wall [C]//2010 International Conference on Computer Application and System Modeling (ICCASM 2010). New York: IEEE Press, 2010, 5: V5-349-V5-352.

[3] 周章勇. 一种三通道球带幕视景系统的开发[J]. 航空维修与工程, 2018(8): 30-33.

[4] PORTALÉS C, ORDUÑA J M, MORILLO P, et al. An efficient projector calibration method for projecting virtual reality on cylindrical surfaces [J]. Multimedia Tools and Applications, 2019, 78(2): 1457-1471.

[5] FURUKAWA R, NAITO M, MIYAZAKI D, et al. Auto-calibration method for active 3D endoscope system using silhouette of pattern projector [C]//Image and Video Technology. Heidelberg: Springer, 2018: 222-236.

[6] 邓晴莺, 李国翬, 王宝奇, 等. 某飞行模拟器视景系统的设计与实现[J]. 兵工自动化, 2016, 35(8): 75-79.

[7] 邓晴莺, 李国翬, 王宝奇, 等. 大下视场飞行模拟器视景系统的设计与实现[J]. 系统仿真技术, 2016, 12(2): 123-129, 139.

[8] BROWN M, MAJUMDER A, YANG R. Camera-based calibration techniques for seamless multiprojector displays [J]. IEEE Transactions on Visualization and Computer Graphics, 2005, 11(2): 193-206.

[9] RASKAR R, BROWN M S, YANG R G, et al. Multi-projector displays using camera-based registration [C]//Proceedings Visualization '99. New York: IEEE Press, 1999: 161-168.

[10] 刘立坤, 刘海波. 广角摄像机标定及畸变图像修正方法研究[J]. 舰船电子工程, 2018, 38(5): 77-80.

[11] 赵永强. 直升机飞行模拟器视景仿真系统的设计与实现[D]. 北京: 北京邮电大学, 2010.

[12] 董鸿鹏, 王春财, 张波. 飞行模拟器视景系统的设计与实现[J]. 计算机应用, 2018, 38(S1): 228-231, 235.

[13] 徐泽骅, 李胜.面向大规模户外场景的实时绘制系统[D]. 北京: 北京大学, 2017.

[14] AHMED A. Geometric correction for uneven quadric projection surfaces using recursive subdivision of Bézier patches [J]. ETRI Journal, 2013, 35(6): 1115-1125.

Geometry Correction Method for Projection onto Spheres

WANG Ming-dong1, GAI Meng2,3, LAI Shun-nan2,3, WANG Zhen4

(1. School of Electronic and Computer Engineering, Peking University Shenzhen Graduate School, Peking University, Shenzhen Guangdong 518055, China; 2. School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China; 3. Beijing Engineering Technology Research Center of Virtual Simulation and Visualization, Peking University, Beijing 100871, China; 4. Shenyang Ligong University, Shenyang Liaoning 110159, China)

A visual simulation system for flight simulation often uses multiple projectors to simultaneously project a surface to obtain a wider range of viewing angles. When the projector is tilted to the screen or the projection screen is a curved surface, the image is geometrically distorted. Aiming at this problem, this paper proposes a geometric correction method for the dome projection system. Taking a three-channel display system as an example, the present study describes the theoretical principle and correction process of the method in detail. The example results show that after geometric correction, each projection image has no geometric distortion, and the geometrical content of the channel transition is completely consistent. The method is a pure software method, which is small in cost and simple in operation, and can be adapted to different projection scenarios.

sphere; geometry correction; flight simulator; multiple projections; OpenGL

TP 391

10.11996/JG.j.2095-302X.2019040631

A

2095-302X(2019)04-0631-06

2019-03-26；

定稿日期：2019-04-11

国家自然基金重点项目(61632003)；国家自然基金面上项目(61872398)；装备预研基金项目(315050501)；国家重点研发计划课题(2017YFB1002601)

王明冬(1994-)，男，甘肃白银人，硕士研究生。主要研究方向为计算机图形学。E-mail：wmd@pku.edu.cn

赖舜男(1965-)，女，重庆人，工程师，硕士。主要研究方向为虚拟仿真。E-mail：snlai@pku.edu.cn