多测度融合的立体匹配算法研究

亢宇欣，谌贵辉，邓 宇，张军豪

多测度融合的立体匹配算法研究

亢宇欣，谌贵辉，邓 宇，张军豪

(西南石油大学电气信息学院，四川 成都 610500)

针对多测度融合的立体匹配算法的测度选择问题，提出一种基于测度互补系数的测度选择方法。通过该方法选择多种测度进行融合作为匹配代价，并使用改进的半全局算法进行代价聚合，实现多测度融合的立体匹配算法。首先定义互补系数，通过互补系数选择多种相似性测度进行融合作为匹配代价；然后，针对半全局代价聚合使用随机初始化视差图导致立体匹配效果较差的问题，使用基于SURF特征得到的视差作为初始视差进行半全局代价聚合；最后计算视差并优化视差得到最终视差图。实验表明，使用该测度选择方法可以选择互补特征，结合改进的半全局代价聚合方法可以提高立体匹配效果。

多测度融合；测度互补系数；半全局代价聚合；立体匹配

双目视觉模拟人类视觉原理，实现从二维图像获取三维信息。立体匹配是指双目视觉系统针对同一场景在不同角度拍摄到的2幅图像，在搜索图像中找到参考图像对应点的过程。立体匹配的效果决定双目视觉所获取三维信息的精确度，是双目视觉的重要环节。

SCHARSTEIN等[1]将立体匹配算法进行分类与评估，将其划分为匹配代价计算、匹配代价聚合、初始视差计算与视差优化4个相对独立的模块，此后关于立体匹配算法的研究大多沿用此框架。针对匹配代价计算，为解决单一相似性测度对图像特征描述不完全，影响匹配精度的问题，文献[2]提出融合图像灰度信息，将灰度差绝对值之和(sum of absolute differences, SAD)、灰度差平方和(sum of squared differences, SSD)以及水平梯度分量作为匹配代价，在彩色图像上取得更好的效果；陆军等[3]设计了一种SAD与Census变换相融合的相似性测度算法，结合线性平滑项和动态变搜索半径，有效改善条纹误匹配现象。靳太明等[4]提出一种融合颜色特征、Census特征、局部二值模型(local binary pattern, LBP)特征并考虑图像多尺度信息的匹配算法，在多种复杂场景中提高了匹配精度。相比单一测度，多测度融合作为匹配代价具有更好的立体匹配效果，但多种测度的选择还没有较好的方法，多根据经验和测度特性进行选择融合。针对此问题，本文通过定义测度互补系数并使用该系数进行测度选择，实验证明该方法可以选择效果互补的多种测度。

有关匹配代价聚合，门宇博等[5]提出一种自适应多窗口方案，解决存在遮挡时的鲁棒视差估计。常用的代价聚合算法还有双边滤波[6]和引导滤波[7]。此外，还有一种半全局代价聚合算法[8]，该算法的主要思想是通过求多方向一维最优解来模拟全局最优，相比于双边滤波和引导滤波，可以取得更好的代价聚合效果。但是半全局代价聚合使用随机视差作为初始视差，影响算法的精度和效率。针对此问题，本文使用基于加速鲁棒特征(speeded up robust features, SURF)[9]生成的视差作为初始视差进行代价聚合，并通过WTA (winner take all)算法[10]获取视差图并经过视差优化获得最终视差图。实验表明，该立体匹配算法可以取得较好的匹配效果。

1 算法总体框架

针对单一相似性测度不能全面描述图像局部特征的问题，使用多种相似性测度融合作为匹配代价；针对半全局算法使用随机初始化视差在多尺度空间计算导致算法效率低的问题，由于SURF特征描述符具有高效、高匹配率的优点，使用基于SURF特征提取的视差图作为初始视差图进行半全局代价聚合，经过视差计算、左右一致性检验、可信度检验等步骤得到最终视差图。算法总体框架如图1所示。其中，I，I为经过校正的左右图像；[，]为多测度融合的匹配代价；D为基于SURF特征匹配得到的视差图；[,]为半全局代价聚合后的匹配代价；D为使用WTA算法计算得到的初始视差；为经过视差优化后输出的最终视差图。

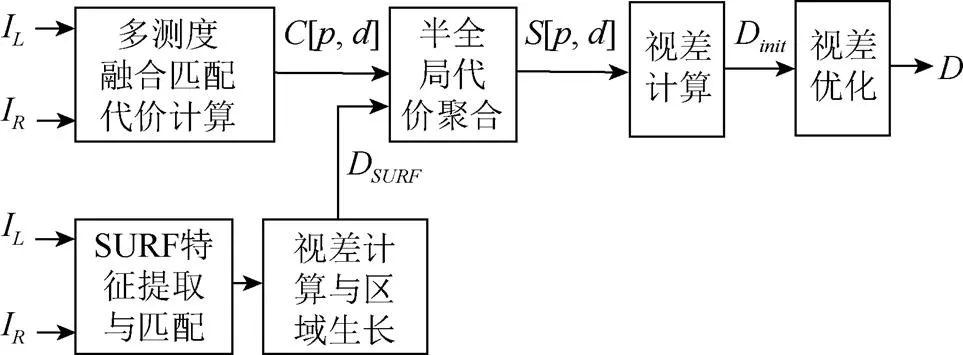
图1 算法流程图

2 多种相似性测度的选择

相似性测度描述的是图像的相似程度，常见相似性测度有SAD、SSD、归一化交叉相关(normalization cross correlation, NCC)[11]、梯度度量(gradient based measure, GBM)、Census[12]变换度量、LBP[13]度量和韦伯局部描述符(Weber’s local descriptor, WLD)[14]度量等。

不同相似性测度使用不同的图像信息和图像特征对图像相似性进行描述，各测度有各自的优势区域。例如SAD测度关注图像灰度信息，以图像灰度差别进行相似度评价；GBM关注图像梯度信息，以梯度差别进行相似度评价。融合多种相似性测度可以更全面地描述图像，进而提高匹配精度，如图2所示。图2(a)中绿色标记为SAD测度正确匹配点，红色标记为GBM，蓝色标记为2种测度均正确匹配的像素点；图2(b)中绿色为SAD测度正确匹配点，红色为SSD测度，蓝色为2种测度均正确匹配的像素点。

可以看出，SAD与GBM重合程度较低，SAD与SSD重合程度非常高。SAD单独作用时正确匹配率为44.38%，SAD分别与SSD和GBM测度融合后匹配正确率为44.51%和52.1%。可见重合程度高的SSD与SAD融合后对于匹配正确率的提升非常小，重合程度低的GBM与SAD测度融合后对于匹配正确率的提升较为明显。本文提出一种基于优势作用区域互补程度的相似性测度选择方法。

图2 测度作用效果

2.1 测度互补系数

每种相似性测度有各自的特点和优势作用区域，设与S为使用和2种相似性测度单独作用所得正确匹配点点集，定义测度互补系数为

其中，为调节系数；ρ为2种相似性测度作用下正确匹配点的相异点数与相同点数之比。显然，该系数越大，表示2种相似性测度正确匹配的相异点越多，互补程度越高；反之互补程度越低，按照此系数进行特征选择，可以选出效果互补的测度。

2.2 基于测度互补系数的测度选择

为验证测度互补系数对测度选择效果的影响，使用Middlebury数据集，根据上述7种测度进行实验验证。首先计算各测度单独作用所得匹配结果，如图3所示。

选择正确率最高的SAD测度作为第一个测度，依次计算其余测度与SAD测度的互补系数，并分别计算其余测度与SAD融合后的匹配效果与正确率，如图4所示。

图4中SAD+GBM测度融合后匹配效果最佳且互补系数最大，选择其作为下一步初始测度。分别计算其余测度与SAD与GBM融合后的匹配效果及互补系数，循环上述步骤，直至融合所有测度，结果见表1。

测度SADSSDLBPNCCWLDCensusGBM 匹配效果 正确率(%)44.3843.8237.8035.5436.7231.7039.18

测度SAD+SSDSAD+LBPSAD+NCCSAD+WLDSAD+CensusSAD+GBM 匹配效果 互补系数0.0510.21460.1470.1950.2770.385 正确率(%)44.5146.4945.8346.3348.9652.10

表1 测度相关系数表

可以看出，每次进行测度融合时，正确率最高的测度其互补系数也最大。基于测度互补系数进行测度选择融合可以选出互补测度并取得更好的匹配效果。

3 半全局代价聚合

半全局算法是使用多方向一维动态规划近似二维动态规划求解能量函数最小值，以提高弱纹理、视差不连续和遮挡区域的匹配精度。

3.1 SGM算法

SGM使用动态规划优化能量函数，求得能量函数最小时的视差，能量函数定义为

其中，()为视差图的能量函数；(,D)为原始匹配代价；后2项为惩罚项，指当前像素和其邻域内所有像素之间的约束。如果和的视差为1，那么惩罚1项；如果大于1，那么惩罚2项。

使用动态规划进行能量函数最小化的求解是NP完全问题。在二维图像上利用动态规划求解及其复杂，但如果只考虑某一行或某一列存在约束不足的问题，使用多方向一维动态规划可以兼顾求解准确度和效率。首先构建单一方向的状态转移方程

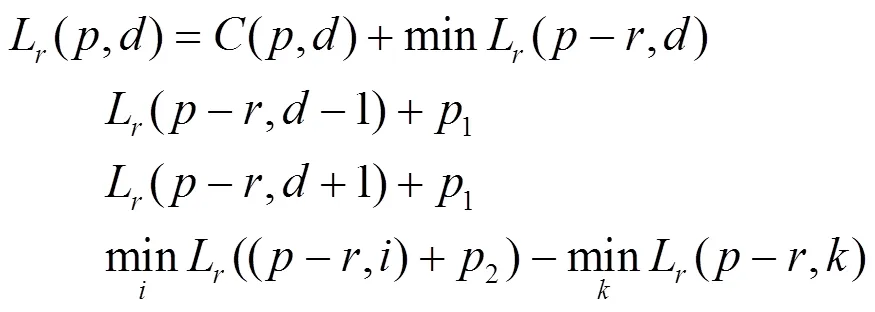
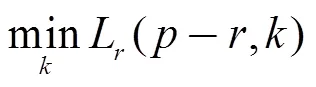
对多个方向使用扫描线优化并对每个扫描线上的L(,)求和，得到图像上点的代价聚合，即

3.2 基于SURF初始视差的SGM代价聚合

由于SGM算法需要一个初始化视差图，原算法随机初始化视差图，并经过多尺度的多次迭代求取最终视差图。算法效果和速度受初始视差图的影响，而基于SURF特征初始化视差图，可提高算法精度和效率。

3.2.1 SURF特征描述符

SURF是对尺度不变特征变换(scale invariant feature transform, SIFT)的优化，是一种鲁棒的局部特征点描述算法，具有尺度缩放、旋转和仿射不变性。SURF特征提取与匹配[9]主要包括以下步骤：

(1) 构建Hessian矩阵，生成所有的兴趣点；

(2) 构建尺度空间；

(3) 特征点定位；

(4) 特征点主方向分配；

(5) 生成特征点描述符；

(6) 基于欧式距离最小化的特征匹配。

3.2.2 基于SURF特征的视差

对左、右2图提取的特征点，以SURF特征描述符欧式距离最小为标准进行特征点匹配，进而求取稀疏视差。使用区域生产算法获得稠密视差，并以此为初始视差图进行SGM代价聚合。

3.3 基于SURF的SGM算法实验

为测试算法效果，设计如下实验。首先按照3.2.1节步骤对左、右2图进行SURF特征提取与匹配，如图5所示。生成关键点如图6所示。

对每个关键点计算Harr小波特征的主方向，并以其为基准方向计算每个特征点的SURF描述符，根据欧式距离最小进行特征点匹配，得到图7匹配结果。

使用对应点横坐标差计算视差，得到稀疏视差图，使用区域生长算法获得稠密视差，如图8所示。

以该视差图作为初始视差图的半全局立体匹配，并与原立体匹配算法进行对比。原算法进行多次下采样，通过多轮迭代，对每轮迭代的结果进行上采样作为下一轮迭代的初始视差。基于SURF特征的半全局算法只在原尺度进行计算，统计2种算法在所有数据集上每轮迭代的平均误匹配率和平均运行时间。实验用计算机CPU主频3.4 GHz，内存8 GB，使用Python语言编程，使用Middlebury数据集中Cones、Teddy、Tsukuba和Venus数据进行实验，实验结果见表2和表3。

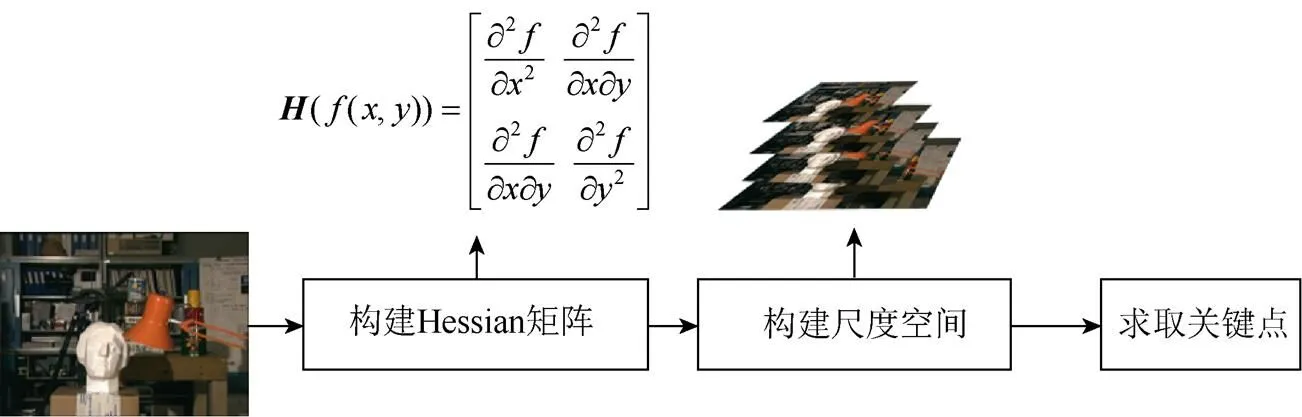
图5 关键点求取过程

图6 关键点标记

图7 SURF特征匹配

图8 区域生长稠密视差图

由表2和表3可以看出，原算法经过5轮迭代后的误匹配率为6.87%，而改进后的算法只需2轮迭代误匹配率稳定在6.79%；原算法总运行时间为137 ms，改进算法所用时间为125 ms。综上，基于SURF特征的SGM算法在算法误匹配率和算法效率方面有一定改善。

表2 SGM算法效果

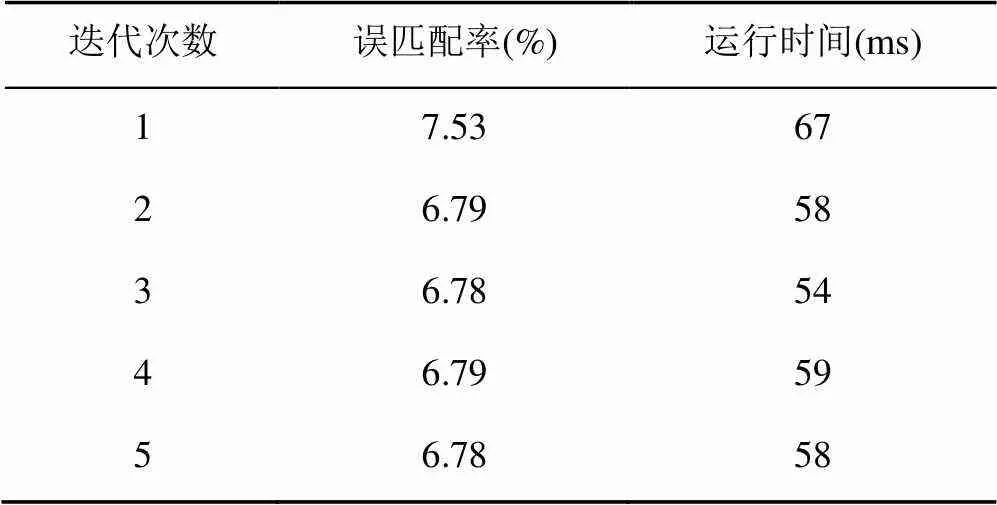
表3 SURF-SGM算法效果

4 算法实验与分析

选择SAD、GBM、Census和WLD4种测度融合作为匹配代价，匹配代价如式(7)所示。使用改进的半全局算法进行代价聚合，利用WTA算法计算初始视差，经过左右一致性检验、可信度检验得到最终视差，按照图1的算法流程进行实验。使用Middlebury数据集作为算法测试数据集，计算机CPU主频3.4 GHz、8 G内存，使用Python编程。

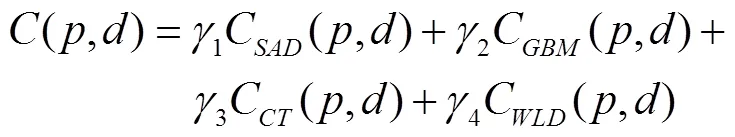
通过实验确定参数，首先使用上述4种测度单独进行匹配，并不断变换测度对应参数，以误匹配率最小时的参数对应测度的参数，求得各测度参数为：λ=32，T=17，T=0.013，T=0.010，T=0.024。然后进行融合测度权重实验，设所有测度权重之和为1，在此约束条件下不断调整各测度权重，以误匹配率最小时的权重作为最终权重，求得各测度权重为：1=0.110，2=0.730，3=0.126，4=0.034。

为验证算法性能，与当前效果较好的SGM、Segment Support算法进行比较，实验结果如图9所示。

原图Segment SupportSGM本文算法真实视差图 Cones Teddy Tsukusa Venus

由图9可以看出，与SGM[15]、Segment Support算法[16]相比，本文算法在纹理区域、视差不连续区域和遮挡区域表现出更好的效果。如Cones数据中方框标记位置为视差不连续区域，本文算法在该区域得到更加平滑的视差；Teddy数据中方框标记位置为纹理区域和遮挡区域，本文算法纹理区域视差平滑、遮挡区域视差轮廓更为清晰。同样地，本文算法在Tsukusa与Venus数据中纹理区域、视差不连续区域也有更好的效果。各算法在Middlebury数据集上不同区域测试结果见表4~7。

由表4~7可以看出，与另2种算法相比，本文算法在多种图像区域匹配效果更佳。另SGM、Segment Support及本文算法的平均误匹配率分别为6.87%，6.58%，4.56%，本文的立体匹配效果较好。

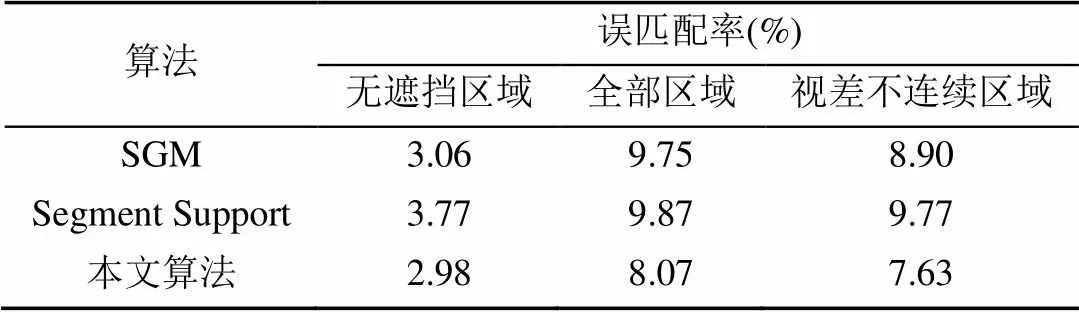
表4 Cones数据上算法效果

表5 Teddy数据上算法效果

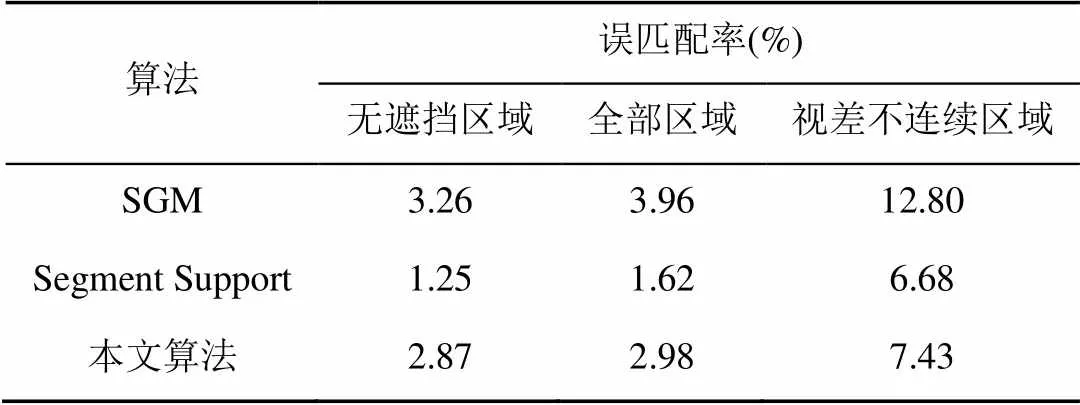
表6 Tsukuba数据上算法效果

表7 Venus数据上算法效果

5 结 论

针对立体匹配算法匹配代价计算与代价聚合步骤，本文提出一种相似性测度选择方法，使用该方法选择相似性测度融合作为匹配代价，实现对图像区域更全面地描述。使用基于SURF特征生成的视差图作为初始视差进行半全局代价聚合。经过实验验证，与当前较为经典的SGM与Segment Support算法相比，本文算法在纹理区域、遮挡区域与视差不连续区域有更好的匹配效果。

[1] SCHARSTEIN D, SZELISKI R, ZABIH R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms [J]. International Journal of Computer Vision, 2002, 47(1-3): 7-42.

[2] TOLT G, KALAYKOV I. Measures based on fuzzy similarity for stereo matching of color images [J]. Soft Computing, 2006, 10(12): 1117-1126.

[3] 陆军, 方莹, 张鑫. 融合AD与Census变换的动态规划立体匹配与遮挡处理[J]. 北京理工大学学报, 2015, 35(12): 1274-1279.

[4] 靳太明, 曾婧, 张翔. 基于多特征融合的多尺度立体匹配算法[J]. 计算机应用, 2016, 36(A2): 139-142.

[5] 门宇博, 张国印, 门朝光, 等. 像素扩展自适应窗口立体匹配算法[J]. 哈尔滨工程大学学报, 2018, 39(3): 547-553.

[6] 宋时德, 李淼, 张健, 等. 面向以多视角立体匹配获取的植株三维点云的去噪方法[J]. 计算机应用, 2017, 37(S2): 141-145.

[7] 闫利, 王芮, 刘华, 等. 基于改进代价计算和自适应引导滤波的立体匹配[J]. 光学学报, 2018,38(11): 257-267.

[8] 吕倪祺, 宋广华, 杨波威. 特征融合的双目半全局匹配算法及其并行加速实现[J]. 中国图象图形学报, 2018, 23(6): 874-886.

[9] 冯亦东, 孙跃. 基于SURF特征提取和FLANN搜索的图像匹配算法[J]. 图学学报, 2015, 36(4): 650-654.

[10] 王玉锋, 王宏伟, 吴晨, 等. 基于共同视域的自监督立体匹配算法[J]. 光学学报, 2019, 39(2): 287-296.

[11] 宋毅, 崔平远, 居鹤华. 一种图像匹配中SSD和NCC算法的改进[J]. 计算机工程与应用, 2006, 42(2): 42-44.

[12] HUMENBERGER M, ENGELKE T, KUBINGER W. A census-based stereo vision algorithm using modified semi-global matching and plane fitting to improve matching quality [C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition - Workshops. Washington, DC: IEEE Computer Society, 2010: 77-84.

[13] 胡敏, 余子玺, 王晓华, 等. G-LBP和方差投影交叉熵的人脸识别[J]. 图学学报, 2017, 38(1): 82-89.

[14] CHEN J, SHAN S G, HE C, et al. WLD: A robust local image descriptor [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1705-1720.

[15] HIRSCHMULLER H. Accurate and efficient stereo processing by semi-global matching and mutual information [C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). Washington, DC: IEEE Computer Society, 2015: 807-814.

[16] TOMBARI F, MATTOCCIA S, DI STEFANO L. Segmentation-based adaptive support for accurate stereo correspondence [M]//Advances in Image and Video Technology. Heidelberg: Springer, 2007: 427-438.

Research on Stereo Matching Algorithms Based on Multi-Measure Fusion

KANG Yu-xin, CHEN Gui-hui, DENG Yu, ZHANG Jun-hao

(School of Electrical Engineering and Information, Southwest Petroleum University, Chengdu Sichuan 610500, China)

Aiming at the measure selection problem of stereo matching algorithm based on multi-measure fusion, a measure selection method based on measure complementarity coefficient is proposed. Using this method, the present study fuses multiple measures as the matching cost, and adopts the improved semi-global algorithm for cost aggregation to realize the stereo matching algorithm of multi-measures fusion. Firstly, the complementary coefficients are defined, and a variety of similarity measures are fused by the complementary coefficients as matching costs. Then, in attempt to solve the problem of poor stereo matching effect caused by semi-global cost aggregation using randomly initialized disparity map, we carried out the semi-global cost aggregation taking disparity based on SURF features as initial disparity. Finally, the disparities are calculated and optimized to obtain the final disparity map. The experimental results show that the complementary features can be selected by using the measure selection method, and the stereo matching effect can be improved by combining the improved semi-global cost aggregation method.

multi-measure fusion; measure complementarity coefficient; semi-global cost aggregation; stereo matching

TP 391

10.11996/JG.j.2095-302X.2019040711

A

2095-302X(2019)04-0711-07

2019-02-01；

定稿日期：2019-03-21

四川省科技计划项目(2016GZ0107)；四川省教育厅重点项目(16ZA0065)；南充市市校科技战略合作项目(NC17SY4001)

亢宇欣(1993-)，男，河北廊坊人，硕士研究生。主要研究方向为计算机视觉、人工智能。E-mail：284260916@qq.com