视差边缘优化的SGM 密集深度估计算法∗

孙 丽 孙彦玮 李 浩

（1.生态环境部南京环境科学研究所 南京 210042）（2.河海大学地球科学与工程学院 南京 211100）

1 引言

在计算机视觉和摄影测量等领域，利用双像立体匹配计算场景的深度信息是目前的一个重要研究方向，在许多立体视觉应用中发挥着重要的作用，比如三维重建、运动检测、驾驶辅助系统等。通常，立体匹配算法可以主要划分为两类：局部算法和全局算法。在局部算法中，一般采用胜者为王（Winner Takes All，WTA）模式匹配候选点，即认为匹配代价最小者为正确匹配，此类方法计算速度快，但是精度较差；全局算法对整幅图像构建一个全局能量函数，并附加平滑约束，以此来优化视差图［1～2］，此类方法视差精度高，但是计算复杂，无法满足实时性要求。2005 年，Hirschmuller［3～4］提出了一种介于局部算法和全局算法之间的半全局密集匹配算法，该方法在满足实时性要求的同时，实现了精确的密集深度估计，得到了众多研究人员的关注与改进。

鉴于在二维空间进行全局能量最小化被证明是NP 困难（Nondeterministic Polynominal-hard）问题，SGM算法将二维能量最小化转换为多个一维路径的能量最小化。为了优化因噪声和遮挡等因素造成的匹配错误，SGM 的能量函数包含三个部分：数据项、惩罚项P1和惩罚项P2，当一维路径中前后两个像素的视差变化较小时，附加一个较小的惩罚项P1，当视差变化较大时附加较大的惩罚项P2。然而在视差边缘区域具有较大的视差变化是合理的，如果附加较大的惩罚项会造成视差图在视差边缘处过度平滑，降低深度估计的精度，因此视差边缘（即深度不连续）区域的精确视差估计仍然具有重要的研究意义。

为了改进深度不连续区域的视差估计精度，研究人员在SGM 算法的基础上提出了许多改进算法。其中，自适应惩罚项算法认为在代价聚合路径上像素灰度值差异越大，该区域是视差边缘的概率越大，因此需要减小惩罚项P2，Banz［5］和Stentoumis［6］对现有的自适应惩罚项优化算法进行了总结与评价，尽管此类算法取得了一定的提高，但是自适应函数中的参数对于不同图像或代价函数的适应性较差，难以推广。另一方面，有研究者将图像的几何特征引入到密集匹配的过程中，例如图像边缘特征和分割结果等。Ko 等［7］利用K 均值聚类方法对图像进行分割，并在每一个分割块中利用视差种子点分别进行代价聚合和视差估计。Liu［8］等根据图像分割结果和初始视差图构建了一个新的能量函数，并通过合并较小的分割块优化能量函数。图像分割算法虽然能一定程度上避免视差边缘的过度平滑，但是分割结果的好坏直接影响了视差估计的结果，如果分割过于密集则深度估计结果不够平滑，如果分割过于粗糙则会忽略掉深度变化的细节特征。因此，利用图像的边缘特征优化视差边缘处的深度估计精度被认为是一种更为有效的方法，因为在视差边缘处一般也会形成明显的图像边缘。Xie［9］等在利用SGM 算法得到视差图的基础上，利用边缘检测和水平、垂直方向的视差线性拟合优化初始视差图，对弱纹理和遮挡区域取得了较好的结果。Zhu［10］将自适应边缘保留导向滤波算法引入到代价计算的过程中，也取得了一定的提高。Chuang［11～12］提出了一种分步的SGM 优化算法，首先利用基于十字的局部密集匹配算法得到初始视差图，然后结合边缘特征自适应计算惩罚项，随后再用SGM算法计算最终的视差图。

为了提高在深度不连续区域的视差估计精度，本文在SGM 算法的基础上，引入图像的边缘特征，提出一种基于边缘视差图优化的密集深度估计算法。与自适应惩罚项和视差平面拟合等后处理算法相比，本文创新性地改进了算法的代价聚合步骤，首先检测立体像对中的边缘特征，然后利用DAISY描述符［13］匹配边缘像素得到边缘视差图，为了避免错误代价在边缘处传播，本文算法利用提取的边缘将每一个代价聚合路径分割为多个子路径，并独立进行代价聚合的计算，同时适当提高非边缘处的惩罚项P2。本文算法既提高了在视差边缘处的深度估计精度，也保持了非边缘区域视差的平滑性。

2 本文算法

本节将详细描述本文算法的实现过程，图1 展示了本文算法的计算流程，算法主要由五个步骤组成：结合AD（absolute difference）和Census的代价计算、边缘视差图计算、代价聚合、视差估计和视差优化，其中视差优化采用左右一致性检查方法。

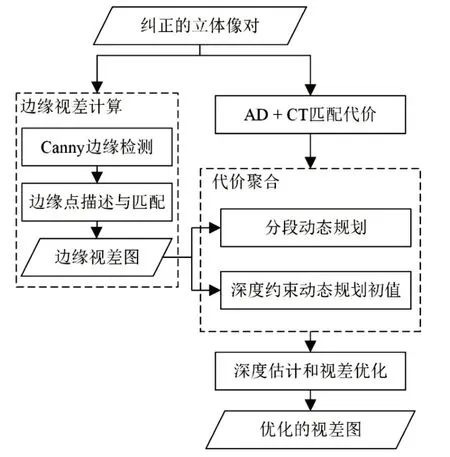
图1 本文算法流程图

2.1 匹配代价计算

在匹配代价计算步骤中，对于立体像对中左图的每一个像素，计算其和视差范围内右图中的每个像素的相似性度量作为匹配代价。本文采用两个应用最为广泛的代价计算方式：像素灰度的绝对差（absolute difference，AD）和Census 变换的汉明距离。灰度差计算简单，但是对光照变化适应性差，Census 变化［14］通过比较中心像素和邻域像素的灰度关系得到一个二值字符串，再计算汉明距离得到相似性度量值，Census变换对于光照变化鲁棒性较好，因此常被用于匹配代价计算［15］。

2.2 边缘视差图计算

在图像中，深度不连续区域通常反映为图像的边缘特征，因此本文首先利用Canny 算法［16］检测图像边缘。在视差范围内，对于左图中的每一个边缘像素，在右图中通常具有数个边缘像素，如图2 所示，图中灰色正方形代表立体像对中的边缘像素，具有灰色轮廓的正方形代表视差范围内右图中的匹配候选点。本文采用DAISY 描述符度量不同边缘像素间的相似性，当左图中该像素与右图中的某一个候选点具有最小的欧氏距离时，则认为该对像素点是正确匹配的边缘点，计算两点间的水平距离即为左图中边缘点的视差值。对左图中每个边缘点重复上述过程即可得到初始的边缘视差图。

图2 边缘像素匹配示意图

由于左图中边缘像素在右图中的正确匹配边缘点并不一定能够被Canny 算法检测出来，或者错误的匹配点有一定的概率具有最佳的相似性度量，因此本文算法使用RANSAC（RANdom SAmple Consensus）算法移除错误匹配点。首先，从初始的边缘视差图中随机选择四对匹配点计算投影变换矩阵；然后，根据投影变换矩阵计算左图中边缘像素点在右图中形成的投影点，如果投影点与真实点之间的距离小于某个特定的阈值（取10 个像素），则认为两点为正确匹配点，视差计算正确，否则放弃该点视差值，将初始视差图中该点灰度值置零。图3 展示了边缘视差图的生成过程，图像中的黑色为背景，轮廓线的灰度值代表每个边缘像素的视差值，为便于观看，将灰度范围标准化到0～255。

图3 边缘视差图生成

2.3 分段代价聚合

代价聚合是立体匹配的一个至关重要的步骤，决定了算法的效率和精度。局部匹配算法采用逐像素的方式评估最小匹配代价，缺少平滑约束和代价聚合过程，所以很容易受到噪声和遮挡的影响产生错误的视差值。因此全局算法将平滑约束加入到代价函数中，通过对不同的视差变化施加不同的惩罚项，构建一个更加精确的能量函数，提高视差估计的精度。对于视差图像D，能量函数E（D）可表示如式（1）：

其中，第一项C(p，Dp)是视差为D 时所有像素匹配代价的和，第二项表示在视差变化等于1 的时候施加一个较小的惩罚项P1，第三项表示在视差变化大于1的时候施加一个较大的惩罚项P2。

全局算法通过最小化能量函数E（D）来获得最优的视差图，但是在二维空间中最小化能量函数是非常困难的，因此SGM 算法将全局的二维能量最小化近似为多个一维路径下的能量函数最小化。通常，一维路径下的代价计算函数Lr(p，d) 可表示为式（2）：

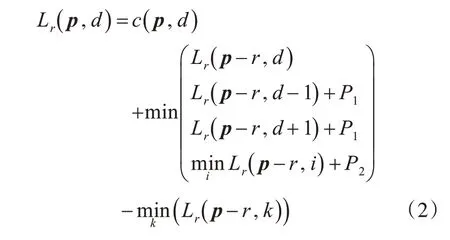
但是，对于视差边缘区域，对较大的视差变化施加一个大的惩罚项，会造成视差边缘的过度平滑，这显然是不合适的，因此本文针对视差边缘区域的精确深度估计问题，结合边缘视差图，提出了一种分段代价聚合算法。

本文算法中，为了避免视差边缘的过度平滑，利用2.2节计算得到的边缘视差图对代价聚合路径L 进行分段，同时将边缘处的视差值作为每一分段的初始视差值分别进行代价聚合的计算，有效避免了错误代价的累计效应。分段的一维代价计算函数可表示如式（3）。

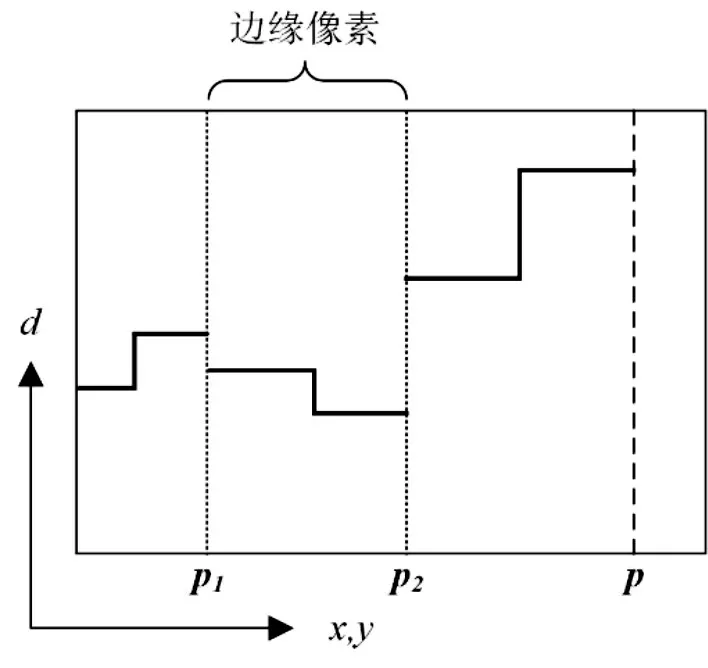
图4 分段约束代价聚合

如图4 所示，图中矩形代表视差空间，不同视差d 处具有不同的视差代价，矩形最左侧是该路径的起点。在原始的SGM 算法中，每一个路径的初始视差值都是取该路径起点处代价最小者的视差，Lr(b，d )=c(b，d )，然后连续代价聚合直至像素点p。本文算法利用边缘视差图分割代价聚合过程，如果像素p1是边缘像素，则令Lr(p，d )= c(p，dedge)，其中dedge是2.2 节中计算出的边缘视差值。本文方法可以有效避免错误代价的传播和视差边缘的过度平滑。

3 实验验证

为了验证本文算法的有效性，我们采用立体基准数据集和真实场景影像对算法进行评估，其中基准数据集采用明德学院Middlebury Stereo Evaluation-Version 3中四分之一分辨率大小图像，并与原始SGM 算法做比较。表1 显示了两种算法的错误像素百分比以及运行时间，错误像素百分比被分为全部像素和非遮挡像素两部分分别进行比较，其中当视差估计值与真值的差大于1 个像素时，该像素被认为是错误像素。实验程序采用C++语言编写，实验平台是Windows 10，Intel Core i7-6700HQ 处理器，8 GB内存，Visual Studio 2015。

由表1 可以看出，本文算法在保持计算时间基本不变的基础上，有效降低了视差图的错误像素百分比，在全部像素和非遮挡像素两类中分别平均下降了1.25 和1.24 个百分点。图5 展示了原始SGM算法与本文算法的实验结果图，从左到右依次为左图像、边缘视差图、原始SGM 视差图以及本文算法视差图，图中用灰色矩形标示出了视差图中改进较为明显区域，从图中可以看出，本文算法在视差不连续区域的表现明显优于原始SGM，视差跳跃边缘更加平滑，与原始图像的边缘更加贴合。

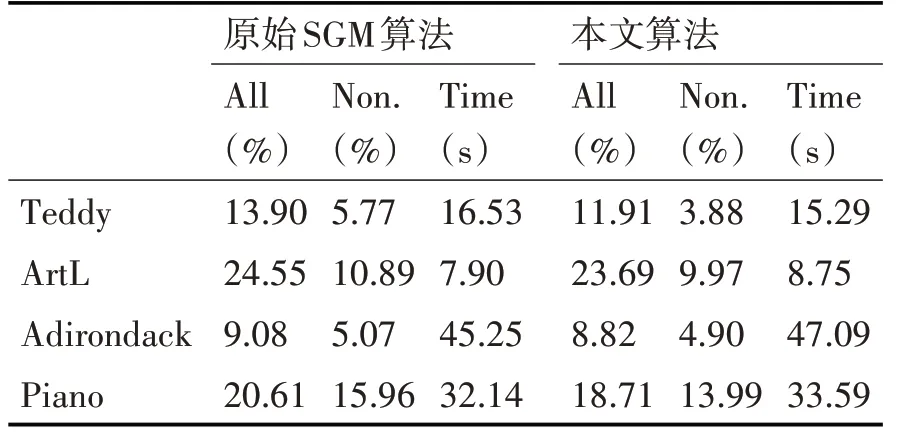
表1 原始SGM算法与本文算法的错误像素百分比与运行时间比较

为了验证本文算法在真实场景中的有效性，我们采用低空无人机影像对算法进行了进一步的评估，实验中选择建筑物较为密集区域的影像，有利于边缘检测，突出本文算法的优势。原始影像及密集深度估计结果如图6 所示，第一列是左图像，第二列是原始SGM 视差图，第三列是本文算法视差图。对比第一行视差图可以发现，本文算法能较好地表现出行道树的视差值，而不会被过度平滑。由第二行可得，本文算法能正确地反映出人字形屋顶的视差变化，减少了屋顶周围的错误视差。对比第三行视差图可知，由于本文算法在非边缘区域增大了视差跳跃的惩罚项P2，因此有效消除了马路等弱纹理区域的错误视差。

4 结语

本文中，我们提出了一种利用边缘视差图优化视差边缘的半全局匹配方法，该方法创新性地利用边缘视差图分割代价聚合路径，避免了大惩罚项对视差边缘的过度平滑。算法利用Canny 算法检测图像边缘，并对边缘点进行DAISY 特征描述与匹配，得到具有视差信息的边缘图像；其次，依据边缘对每个方向的代价聚合路径进行分段，并将边缘视差值作为每一段代价聚合路径的初值，如此反复直至聚合完成。文中利用立体基准数据集和真实场景影像对算法的有效性进行了验证，证明了本文方法在视差不连续区域能取得比原始SGM 算法更好的视差图，对非边缘区域增加惩罚项P2也提高了算法在平滑区域的稳定性。另外，本文采用DAISY描述符对边缘点进行描述，增加了算法的运行时间，描述符的选取与边缘视差图的优化将是下一步的研究内容。