基于速度补偿涂布卷绕系统分数阶PID 控制∗

王啸曦 万振刚 高 翔

（1.江苏科技大学电子信息学院 镇江 212003）（2.无锡鑫德胜自动化科技有限公司 无锡 214000）

1 引言

四电机涂布卷绕系统主要目的为在涂布卷绕过程中保持张力稳定，同时消除相邻传动点间的速度差，提升涂布生产效率。文献［1］中提到使用PID 控制双电机卷绕系统，并给出仿真结果。传统PID 控制结构简单，控制效果良好。但在系统中电机的数量较多的情况下，PID 控制效果也不理想。而分数阶PID［2］有更加灵活的可调参数，在实际应用中面对复杂控制环境可以快速适应。

涂布卷绕系统控制关键在于多电机同步协调控制，在工业中常用的多电机同步控制策略有主从控制［3］与并行控制［4］，随着自动控制技术发展，交叉耦合控制［5］策略被大量运用到双电机控制系统中，并取得良好效果。

针对涂布系统控制要求，根据偏差耦合［6］思想，本文首次提出并设计了综合运用分数阶PID 控制器与速度补偿控制策略的四电机涂布卷绕控制方法，即将各环节负载线速度输出通过速度补偿器整定并反馈至分数阶PID控制器对系统进行控制。

2 卷绕同步控制结构

本文针对四电机卷绕控制结构设计一种线速度补偿器并结合分数阶PID 控制的同步控制策略，构造出四电机同步卷绕控制系统，结构图如图1 所示，V 为给定线速度，V1、V2、V3、V4为放卷、主牵引、副牵引、收卷环节线速度输出信号，MUX 为速度组合器，DEMUX 为速度解析器。速度补偿器主要是将收/放卷以及牵引环节线速度输出值返回至系统中并与其他环节负载线速度输出值做差，经过放大与累加处理输出反馈补偿信号。将补偿信号输入至分数阶PID控制器，从而实现对系统的控制。

图1 控制结构示意图

3 四电机涂布卷绕传动模型

四电机涂布卷绕系统包含放卷环节、收卷环节和两个牵引环节，每个环节由电机驱动。每个驱动环节上有速度检测装置，并且每两个环节之间有张力检测装置，结构如图2 所示，从右至左以此为放卷环节、主牵引环节、副牵引环节和收卷环节。

图2 四电机涂布卷绕系统传动模型

涂布卷绕生产设备张力大小主要由辊轴间的速度差决定。文献［7］给出张力公式为

式中V2为收卷电机速度，V1为放卷电机速度，K 为张力系数。

由式（1）可知，张力大小与相邻传动点之间线速度差的积分成正比，因此张力控制在本质上是卷绕系统中相邻两辊轴的线速度控制。

根据式（1）可得出卷绕速度和张力表达式：

式中：ωi、Ri、Vi分别为各辊轴角速度、旋转半径和线速度，Ti为各辊轴之间张力，Ki为各驱动环节间张力系数，i为各个驱动环节序号。

系统运行中，牵引轴半径保持恒定，收/放卷轴半径则动态变化，因此要使收/放卷轴线速度与牵引轴一致，需动态调控制其转速。收/放卷轴半径与时间关系表达如下：

式中h 为布料厚度，V1、R1为放卷电机速度与半径，V4、R4为收卷电机速度与半径。由式（4）、式（5）可知：收/放卷轴的半径变化率由瞬时转速决定。

依据上述式（2）～（5），完成拉氏变换，可以得到数学模型：

式（6）中，R10、R40分别为放卷环节负载与收卷环节负载初始旋转半径；R1、R2、R3、R4分别为放卷环节、主牵引环节、副牵引环节、收卷环节负载运动半径；同样，V1、V2、V3、V4为各环节负载线速度；ω1、ω2、ω3、ω4为各环节角速度；T1为放卷张力、T2为牵引张力、T3为收卷张力。

4 控制器设计

4.1 速度补偿器

速度补偿方法为多电机控制策略关键，常用多电机控制策略为主从控制、并行控制，但用于涂布卷绕系统都无法达到精确的效果；交叉耦合控制不适用三台以上电机。

为使各辊轴线速度一致，根据偏差耦合控制策略思想以及四电机卷绕控制模型，文本设计一种改进速度补偿器，补偿器结构如图3所示。

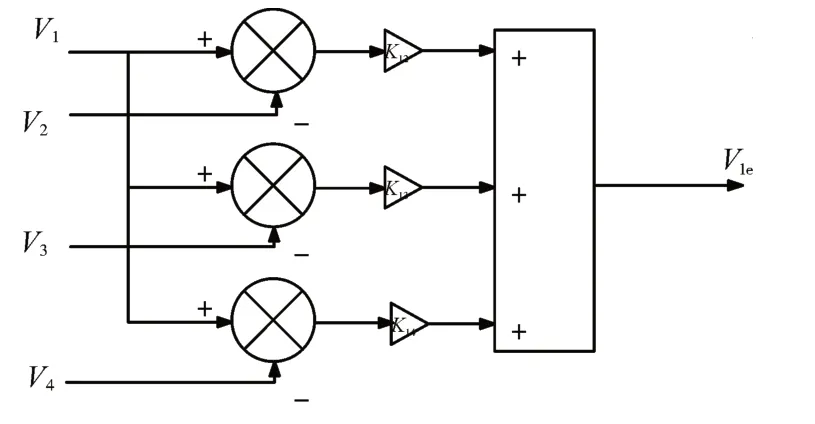
图3 速度补偿器结构图

以放卷环节为例，其负载线速度反馈误差信号为

其中，E 为反馈误差，V 为给定线速度，V1为放卷环节负载线速度输出值。当反馈信号为单一环节线速度输出值时，单一环节发生波动时并不能影响其他环节，导致产生速差，使系统不稳定。

如结构图所示，各环节速度补偿器输出补偿信号为

其中，V1e、V2e、V3e、V4e分别为各环节的线速度补偿信号，Kij为增益系数，eij为各环节之间的速度差，如下所示：

其中，V1、V2、V3、V4分别为放卷环节、主牵引环节、副牵引环节以及收卷环节负载线速度。

由式（7）、式（8）、式（9）可得通过速度补偿器后反馈速度误差信号为

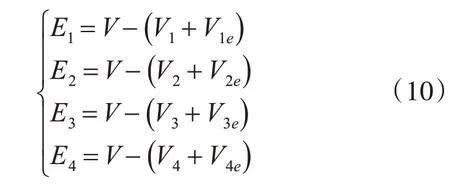
其中，E1、E2、E3、E4分别为放卷环节、主牵引环节、副牵引环节以及收卷环节负载线速度误差信号，V为给定线速度值。

根据以上多式可知，速度误差反馈信号通过各环节间的速差整定得到，即在单一环节线速度发生波动时，其他环节可根据波动情况随动，保持整体速度一致，其张力波动也可以控制至最小范围。

4.2 分数阶PID控制器

通过速度补偿器控制策略整定反馈信号达到同步控制要求后，为使整体系统能够得到更精确的控制效果，本文使用分数阶PID 控制器完成系统控制。

分数阶PID 控制器一般形式为PIλDμ［8～10］。比传统PID 多两个可调节参数：微积分的阶数λ、μ。分数阶PID的传递函数为

根据永磁同步电动机的数学模型［11～13］，本文所选取收/放卷电机以及牵引电机数据如表1所示。

表1 电机参数表

以牵引环节为例，根据所建立模型以及电机参数表，其速度的传递函数公式为

加入整数阶PID［14］控制后，系统传递函数为

根据频率特性，可得出整数阶PID 最优控制参数近似等于：KP=150、KI=0.75、KD=2.5。在分数阶PID 控制器的设计中，以此三个参数作为控制器的参数KfP，KfI，KfD。

由于分数阶PID 转化成整数阶时是无限维，为了确定精确表达式，本文使用Oustaloup 滤波算法对分数阶微积分算子进行近似，方便分析。（ωb，ωh）为近似的频段范围，N 为近似阶次。Sλ、Sμ统一为分数阶微积分算子Sα，其近似化有理传递函数为［15］

式中K为增益。

根据牵引环节模型，将微积分算子近似频率范围设定在（0.001，1000）之间，通过比对，当近似阶次N=4 时效果最优。此时取积分阶数λ=0.9，μ选定在（0.1，0.9）范围，间隔0.2，对比选取最优的微分阶次。图2 显示了不同μ值下模型的阶跃响应曲线：

图4 不同μ值下阶跃响应

由上图可以得出，当取λ=0.9，μ=0.1，为最佳控制参数。根据最优整数阶PID 控制参数：KP=150、KI=0.75、KD=2.5，得出牵引环节分数阶PID 控制器传递函数为

针对放卷环节与收卷环节控制器设计，放卷满载转动惯量取3.21kg·m2，收卷空载转动惯量取3.06 kg·m2。分数阶PID 控制器中积分项与微分相的阶次为λ=0.9，μ=0.1，得放卷环节与收卷环节控制器传递函数分别为式（19）与式（20）：

5 仿真结果分析

为了验证基于速度补偿分数阶PID 控制卷绕系统的可行性，电机参数如表1 所示。仿真效果与PID 控制比对，并对比主从控制和并行控制。放卷满载转动惯量取3.21kg·m2，收卷空载转动惯量取3.06 kg·m2，设定系统参考线速度为10m/min，参考张力为10N。

图5 速度响应曲线

图5（a）、5（b）、5（c）、5（d）分别为放卷环节，主牵引环节、副牵引环节以及收卷环节的负载线速度在分数阶PID 与PID 控制下对比，实线为分数阶PID 控制，虚线为PID 控制。如图所示，在分数阶PID控制下，各个环节速度调节时间均在0.6s左右，而在PID控制下的调节时间达到0.9s左右。

为建立稳定张力，设定各环节响应过程中控制器参数如下：

放卷环节：KP=12.45、KI=0.3、KD=1.5；牵引环节1：KP=40、KI=0.5、KD=2.5；牵 引 环 节2：KP=60、KI=0.85、KD=2.5；收卷环节：KP=101、KI=1.1、KD=1；其中阶次λ=0.9，μ=0.1。

图6（a）、6（b）、6（c）分别为放卷张力、牵引张力以及收卷张力分别在分数阶PID 与PID 控制下对比，实线为分数阶PID 控制，虚线为PID 控制。由图可知，在分数阶PID 控制下，各环节张力调节时间均在0.6s左右，远优于PID控制。

图6 张力响应曲线

进一步验证系统的抗扰动性能，设定系统参考线速度为10m/min，在t=1.5s 时主牵引环节突加负载转矩TL=10N·m，观察系统同步误差。

图7、图8、图9中（a）、（b）、（c）分别为放卷环节与主牵引环节、主牵引环节与副牵引环节、主牵引环节与收卷环节负载线速度同步误差曲线，由图可知，在t=1.5s 时突加负载转矩后，速度补偿控制能极小地消除误差，各环节负载线速度随动性较好，速差不超过0.3m/min，在0.1s 内恢复稳态。而主从控制与并行控制同步误差大，稳态时间长，无法达到预期控制效果。

在主牵引环节加上方差为1N·m 的连续负载干扰转矩，观察张力稳定性。

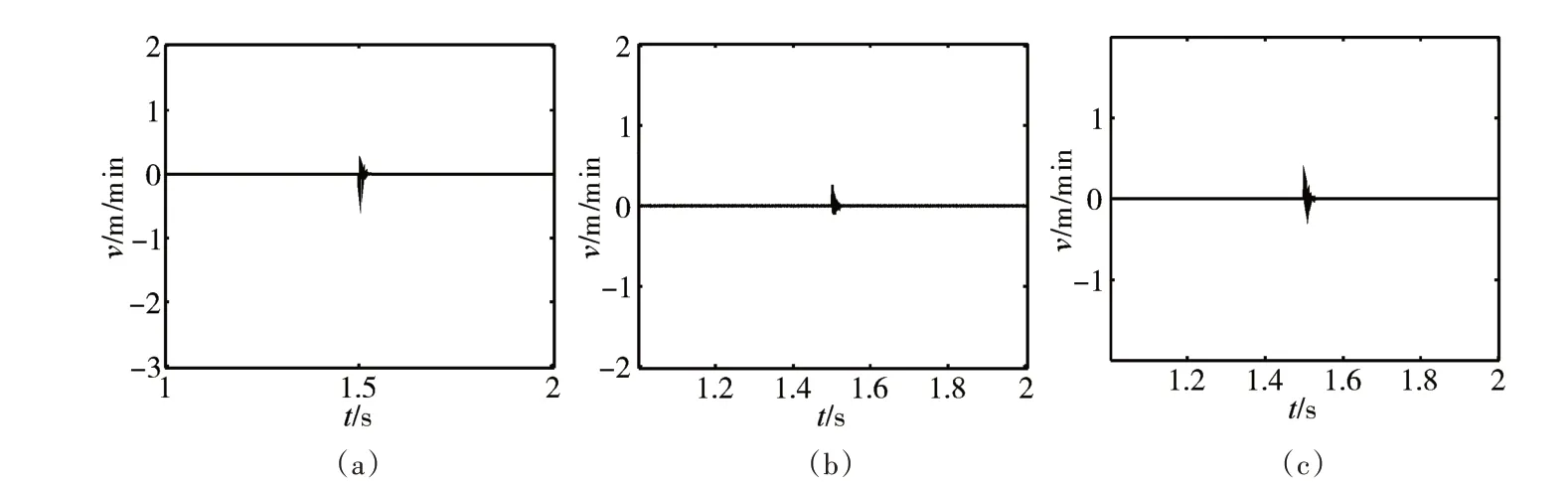
图7 同步误差曲线

图8 并行控制同步误差曲线

图9 主从控制同步误差曲线

图10 张力误差曲线

图10 中三条曲线为系统三段张力波动曲线，可知使用基于速度补偿分数阶PID 控制后，当单一环节负载存在连续误差时，由于各环节负载速度具有随动性，产生速差极小，其张力波动范围在0.5%以内，不影响系统稳定运行。

6 结语

本文针对四电机涂布卷绕控制系统提出了一种综合运用分数阶PID 控制器与速度补偿的智能控制方法，通过仿真实验得出以下结论：

1）使用速度补偿控制策略可在系统单一环节速度发生变化后，较好地消除误差并控制其他环节随动，保持系统整体速度一致，减小张力变化。

2）分数阶PID 控制器可以有效提高卷绕控制系统的响应速度和控制精度；

3）综合运用分数阶PID 控制器与速度补偿方法可实现针对四电机涂布卷绕系统的整体有效控制，即在系统存在负载转矩扰动等复杂工况下可保证系统高效稳定运行。

因此该方法在多电机涂布卷绕控制系统中具有较高的可行性和实用性。