基于RPCA和视觉显著性的风机叶片表面缺陷检测

曹锦纲，杨国田，杨锡运

基于RPCA和视觉显著性的风机叶片表面缺陷检测

曹锦纲1，杨国田2，杨锡运2

(1. 华北电力大学控制与计算机工程学院，河北 保定 071003；2. 华北电力大学控制与计算机工程学院，北京 102206)

针对风机叶片表面缺陷检测问题，提出了一种基于鲁棒主成分分析(RPCA)和视觉显著性的表面缺陷检测方法。在RPCA的基础上，通过增加噪声项和考虑像素的空间关系，以利于缺陷的分割，即通过F范数正则项抑制高斯噪声和光照不均，利用Laplacian正则项约束像素的空间关系，以保持显著图中具有相似显著值且空间相邻超像素的局部一致性和不变性。首先，对输入的风机叶片表面图像进行超像素分割和特征提取，得到图像的特征矩阵；然后，利用改进的RPCA法得到稀疏矩阵，根据稀疏矩阵和视觉显著性方法计算出缺陷区域的显著图；最后，优化显著图并采用自适应阈值分割实现缺陷的检测。通过实验仿真和对实验结果定性定量分析，表明该方法具有较高的准确率。

RPCA；视觉显著性；缺陷检测；风机叶片

风机叶片是风力发电机组的力源和主要承载部件，也是最昂贵和最易受损的部件，暴风雨、风沙和雷击等都有可能损伤叶片。随着国内风电场运行时间的增加，风机叶片表面缺陷的快速、高效检测变得越来越重要。传统的人工巡检已难以满足要求，随着图像处理技术的发展，无人机巡检等基于机器视觉的缺陷检测得到了快速发展。基于机器视觉的缺陷检测的关键是将缺陷区域从图像中分割出来，生成缺陷的二值图像。常见的图像分割方法主要包括基于统计、滤波和模型3种[1]。当前，深度学习发展迅速，具有较好的性能且多用于分类，但实际应用于检测的较少，原因有2点：一是缺陷数据库太小，无法满足深度网络训练学习的要求而易导致过拟合；二是大规模缺陷图像收集费时且人工标记开销大。

近年来，鲁棒主成分分析(robust principal component analysis, RPCA)[2]被应用于图像重建、目标识别和缺陷检测等。在进行缺陷检测时，可将有缺陷的图像分为无缺陷背景纹理区和缺陷前景区2部分，分别用低秩矩阵和稀疏矩阵表示。文献[3]用RPCA批量检测同一场景、同一光源下的多幅图像，将一幅图像变成矩阵的一列，为了能将图像以低秩和稀疏矩阵表示，待检图像必须有多幅；文献[4-5]利用RPCA，通过低秩分解得到织物疵点显著图，并对显著图优化和阈值分割完成疵点检测。文献[6]用低秩分解得到缺陷特征矩阵，获得缺陷区域的初始显著图，再利用超像素分割和视觉显著性精确定位太阳能电池片表面缺陷区域；文献[7]将RPCA应用于纸病图像的分割，但纸病图像背景情况单一；文献[8]用RPCA对铝箔图像进行低秩分解，实现背景图像和缺陷图像的分离，达到铝箔表面缺陷检测的目的。但当表面存在较大低对比度缺陷区域时，缺陷检测的连续性不能令人满意。文献[9]将低秩分解应用于LCD表面缺陷检测，但主要针对背景纹理简单的LCD图像，扩展性不强；文献[10]提出了带有噪声项的RPCA模型—(NRPCA)，用于织物缺陷的检测，该模型忽视了稀疏像素间的连接性，无法检测连续的缺陷区域；文献[11]用F范数代替RPCA模型中的核范数和2范数，而F范数并不与核范数和2范数相同，因此有些情况，检测效果并不好，检测的缺陷区域边界很模糊。

以上采用RPCA进行缺陷检测时，均未考虑图像的光照问题，而通过无人机巡检采集的风机叶片图像，由于图像的拍摄角度不同，光照不均不可避免。同时，为了更好地检测出连续的缺陷区域，本文提出了一种考虑像素空间关系和带有噪声项的RPCA风机叶片表面缺陷检测方法，以抑制高斯噪声和光照不均的影响。

1 本文方法

图1是本文风机叶片表面缺陷检测流程图。

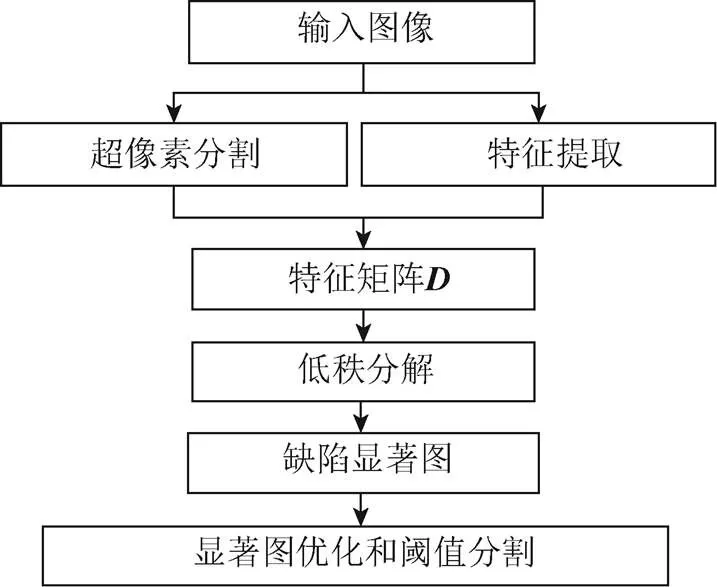
图1 风机叶片表面缺陷检测流程图

1.1 超像素分割

超像素分割将具有相似特征的像素聚集在一起，形成一个超像素。以超像素作为图像处理的基本单位可以大大降低维度和剔除一些异常像素点。而风机叶片的表面缺陷部分和无缺陷部分，具有不同的特征(颜色和纹理等)，通过超像素分割可将缺陷部分有效的聚集起来。本文采用SLIC算法[12]实现超像素分割。

1.2 特征提取

本文提取图像的颜色特征、Gabor特征和方向可控金字塔特征。

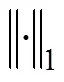
(1) 颜色特征。采用图像的RGB 3颜色通道以及HSV颜色空间的H和V2通道共5个特征表示叶片图像的颜色特征。每个超像素所包含像素的平均颜色特征，即为超像素的颜色特征，则图像的颜色特征矩阵5×K，其中为超像素的个数，以下同。

(2) Gabor特征。Gabor滤波器的频率和方向与人类的视觉系统类似，特别适合于纹理表示与判别。用Gabor特征能够描述图像纹理信息，而且其具有良好的空间局部性和方向选择性，对光照等具有一定的鲁棒性。本文对图像采用3尺度8方向进行Gabor滤波，其Gabor特征矩阵24×K。

(3) 方向可控金字塔特征。方向可控金字塔具有尺度和方向子带的图像表示，且不会混叠。本文对缺陷图像采用2尺度6方向滤波，其方向可控金字塔特征矩阵12×K。

将上述图像的3种特征组合在一起，便构成图像的特征矩阵41×K。

1.3 改进的RPCA方法

RPCA的基本思想是将受到干扰的矩阵分解成低秩矩阵和稀疏矩阵两部分，即

=+(1)

其中，为特征矩阵；为低秩矩阵；为稀疏矩阵。将式(1)转化为式(2)的最优化问题，即

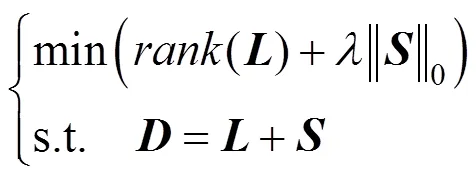
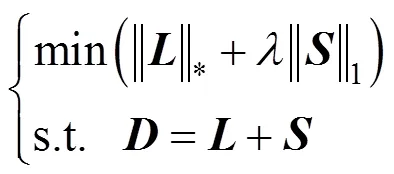
为实现对光照不均的抑制和能够检测连续的缺陷区域，在RPCA的基础上，增加F范数正则项抑制光照不均的问题，利用Laplacian正则项约束像素的空间关系，则式(3)可变形为

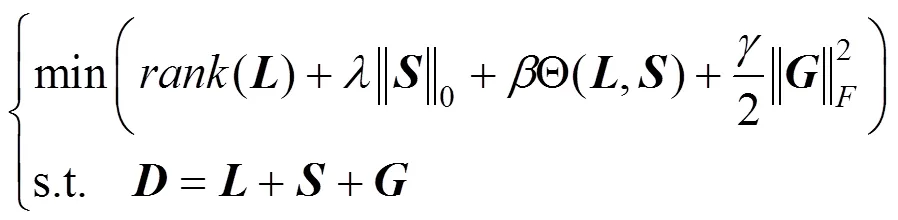
其中，,,,×K分别为特征矩阵、低秩矩阵、稀疏矩阵和噪声矩阵，为超像素数目，为特征数(本文取值为41)；(,)为Laplacian正则项；为矩阵的F范数；，和为罚参数。Laplacian正则项可以保持显著图中具有相似显著值并在空间相邻的超像素的局部一致性和不变性，从而有利于缺陷的分割，而噪声项则可以抑制高斯噪声和光照不均。

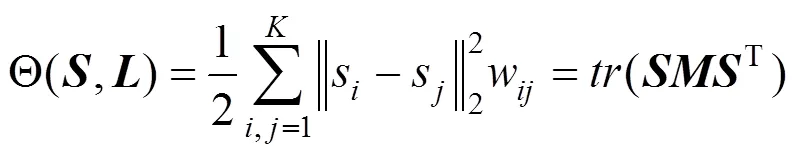
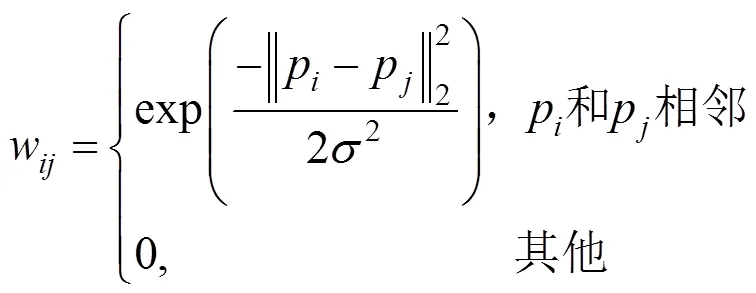
其中，w，×K为超像素间的连接权值矩阵；为CIE-Lab颜色空间中超像素和在、和颜色通道的欧氏距离，×K为Laplacian矩阵，即

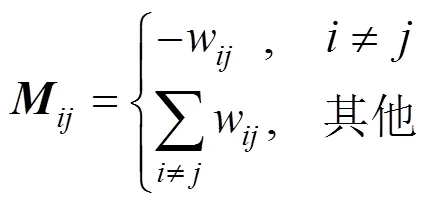
式(4)经过松弛后，变为

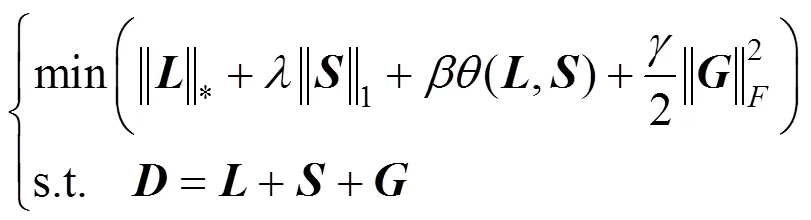
令=，则

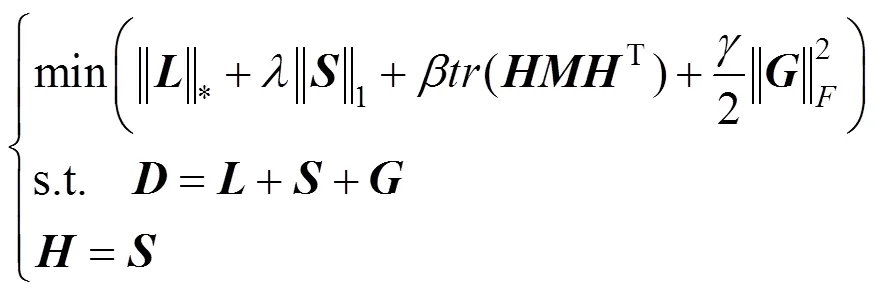
其增广拉格朗日函数为

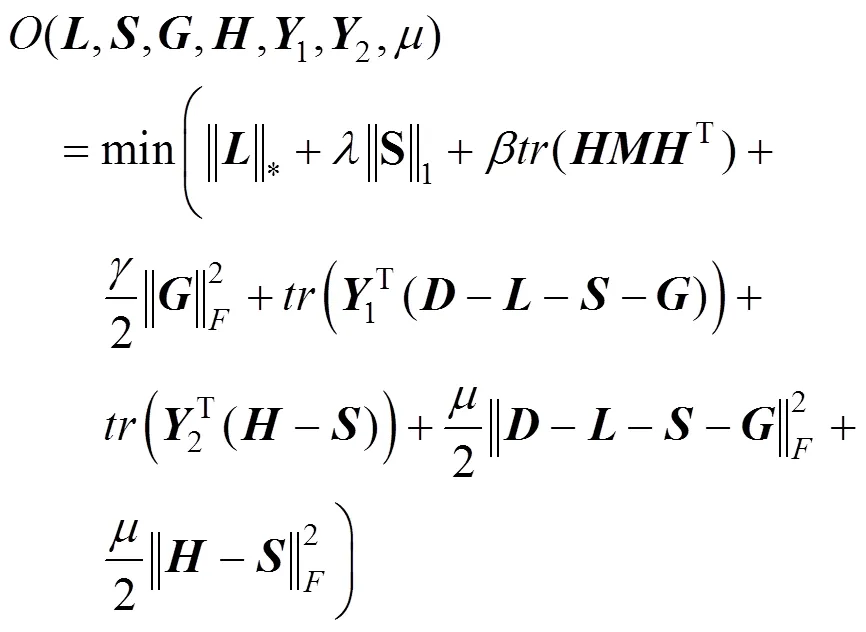
因此，式(10)可转换为优化问题，即

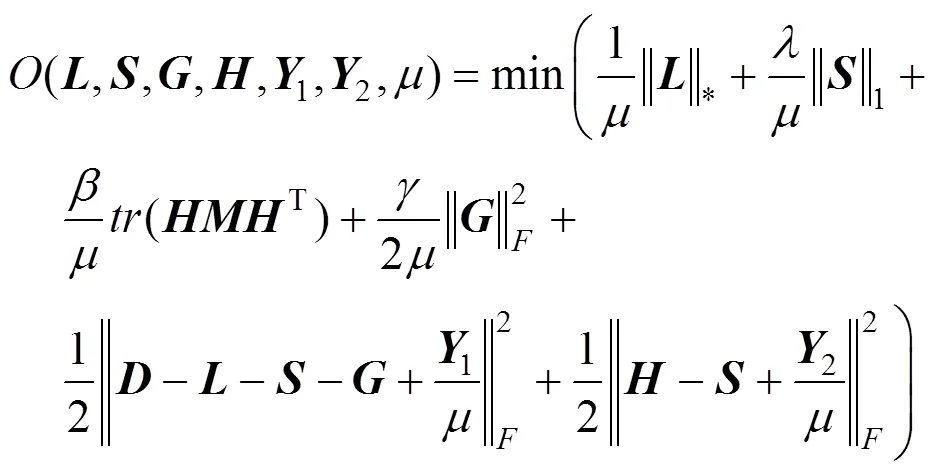
利用ADM算法[13]求解，，和。

(1) 更新

对求导，并令其值为0，得到

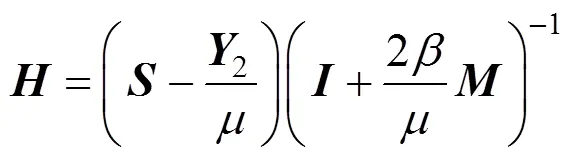
(2) 更新

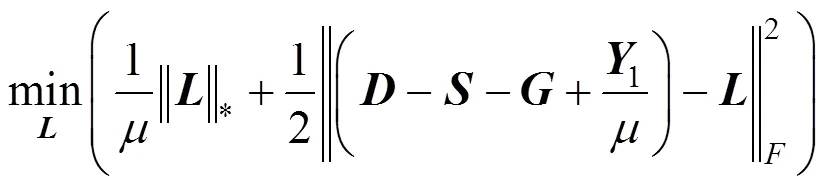
则

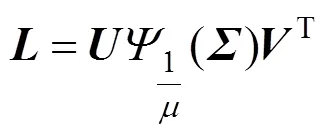
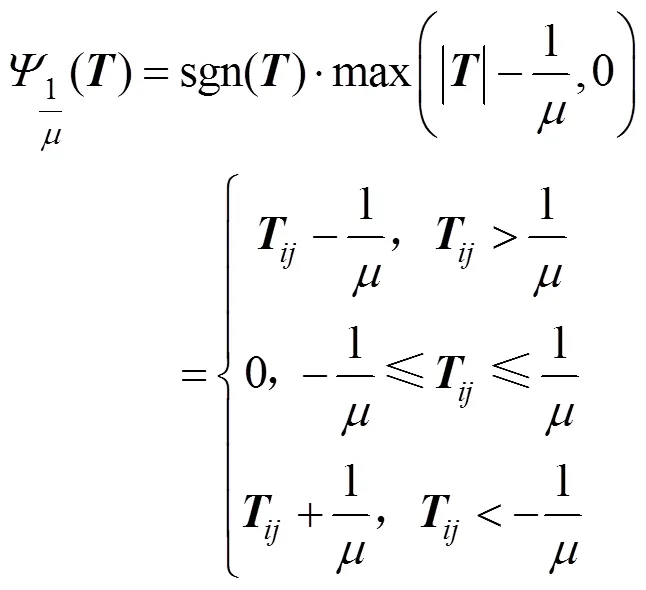
(3) 更新

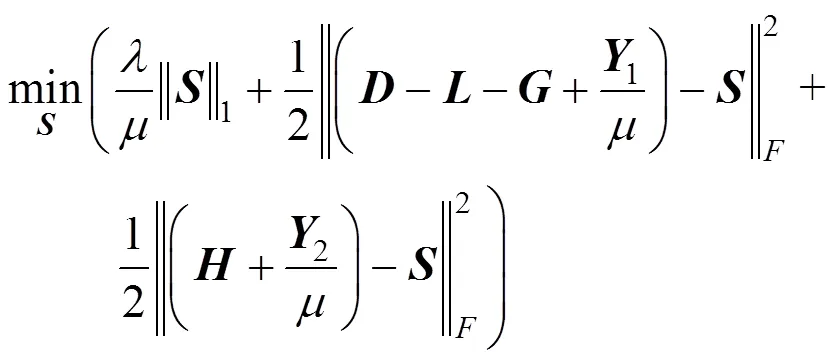
整理得

则，

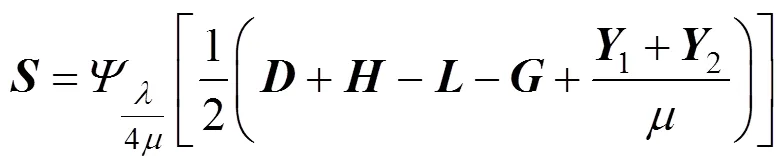
更新

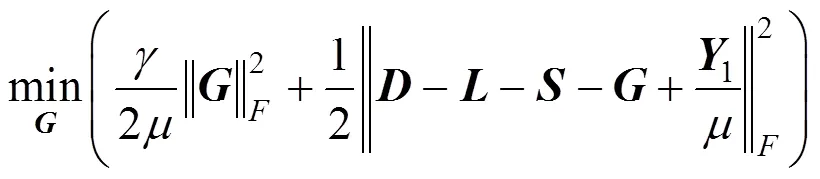
对求导，并令其等于零，则

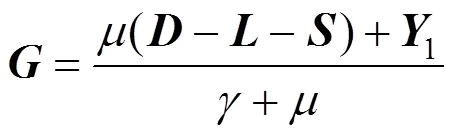
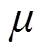
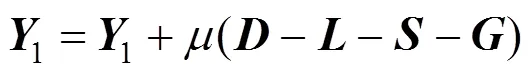
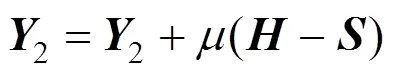
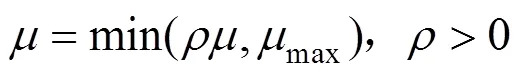
算法描述：

输入：特征矩阵。

输出：低秩矩阵，稀疏矩阵和噪声矩阵。

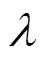
步骤2. 按照式(13)，(15)，(19)和式(21)更新，，和；

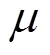
步骤4. 更新迭代次数；

步骤5. 判断是否达到最大迭代次数max。是，则结束，输出，和，否则转步骤2。

1.4 图像缺陷区域显著图及其优化

由所得稀疏矩阵，可计算超像素的显著值，即

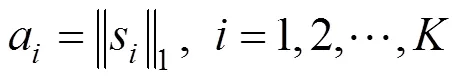
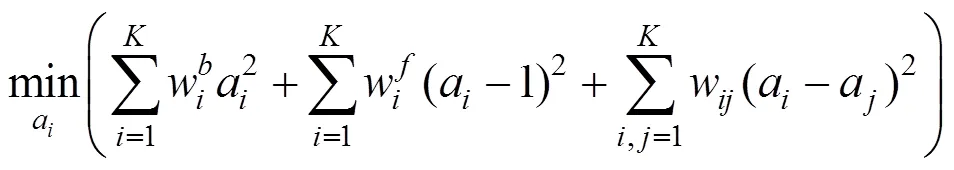
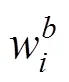
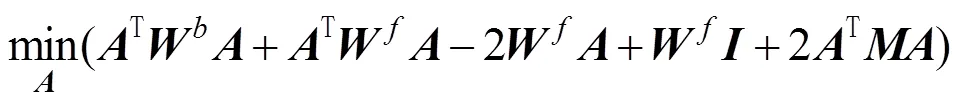
通过对求导，并令其为零，得

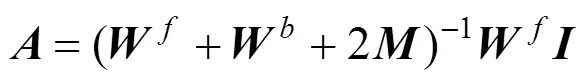
通过该优化，缺陷区域的显著值增大，非缺陷区域的显著值减小，从而使缺陷的显著图更加突出，如图2所示。最后对显著图使用大津法进行自动阈值分割，二值图像中的白色部分即为表面缺陷。

2 实验结果与分析

(1)定性比较。图3为本文算法和相关算法检测的显著图。其中，图3(1)和(2)分别是原始图像和人工标注图；图3(4)和(5)分别为RPCA和NRPCA算法，其检测连续的缺陷区域效果较差，对光照不均图像的缺陷检测基本失效，虽然NRPCA通过增加F范数正则项，在一定程度上抑制了噪点，但是检测效果并不理想。PNRPCA在NRPCA的基础上，考虑了稀疏像素间的权值，从图3(6)可以看出，在图像光照均匀时，检测效果较好，但是图像光照不均时，则出现很大的误检。基于视觉显著性的SR和FF算法，缺陷的显著性图较为模糊、难以分辨，检测效果很差，如图3(7)和(8)所示；图3(9)是FT归一化后的显著图，其能够检测出缺陷区域，但是也存在大量的干扰，总体检测效果较差；从图3(10)可见，CA算法的显著图能够突出缺陷区域，但是边界较为模糊，不利于区域的准确定位。如图3(3)所示，对于连续缺陷区域和光照不均图像，均能够较准确的检测缺陷区域，从而说明了本文算法的可行性和有效性。

(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (a) 图像1(b) 图像2(c) 图像3(d) 图像4(e) 图像5(f) 图像6(g) 图像7(h) 图像8

(2) 定量比较。本文采用了PR曲线、F-measure曲线、ROC曲线和AUC图对缺陷区域检测的精确性进行评价。查准率()、查全率()、假阳率()和真阳率()定义为

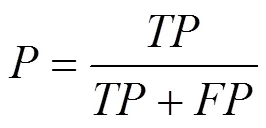
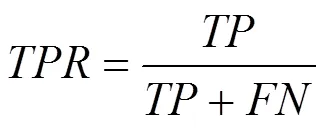
其中，、、和分别为显著图中的真阳数、真阴数、假阳数和假阴数。

PR曲线以“P(Precision)”为纵坐标，“R(Recall)”为横坐标。PR 曲线越靠近右上角性能越好。图4为各算法的PR曲线图，从图中看出，本文算法相较其他算法，曲线更加靠右上角，说明本文算法在相同情况下，具有更高的“查准率”和“查全率”。

由于查准率和查全率无法全面地对显著性图进行评估，又采用了F-measure评价指标，即查全率和查准率在非负权重下的加权调和平均值。其综合了和的结果，当measure较高时，说明方法比较有效

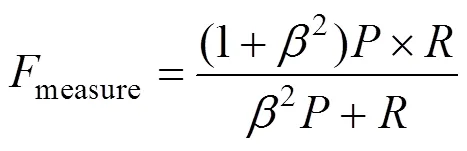
根据经验，一般取值为0.3。图5是各算法的F-measure曲线，从图中可以看到，本文算法具有更高的Fmeasure值。

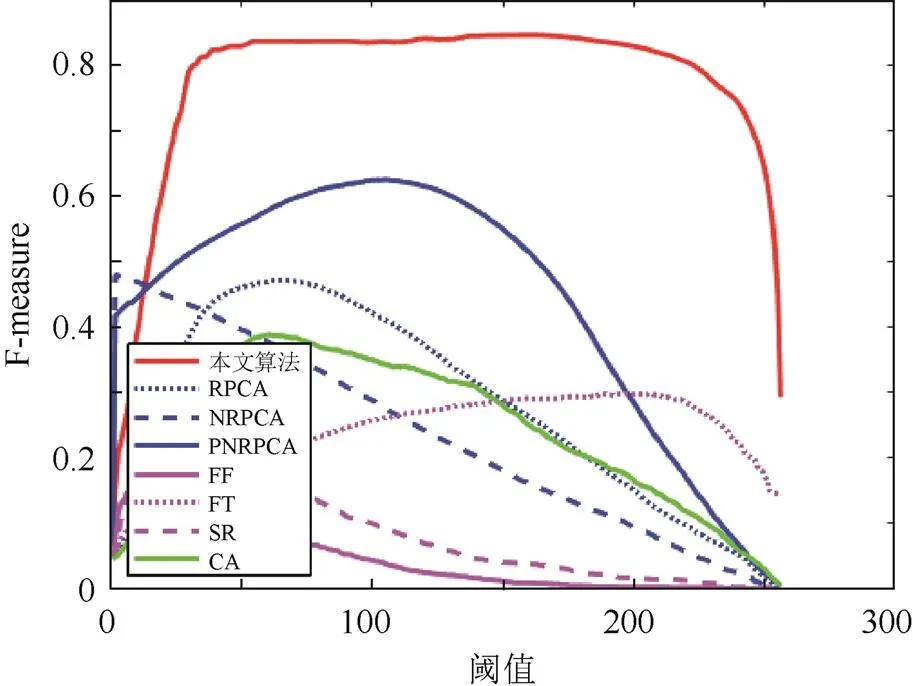
图5 各算法F-measure曲线比较

以FPR为横轴，TPR为纵轴，即可得到ROC曲线，ROC曲线的面积值即为AUC (area under curve)，AUC越大，准确率越高。图6和图7是各算法的ROC曲线和AUC图。从图7可以看到，只有本文算法的AUC大于0.9，说明本文算法具有较高的准确率。

图6 各算法ROC曲线比较

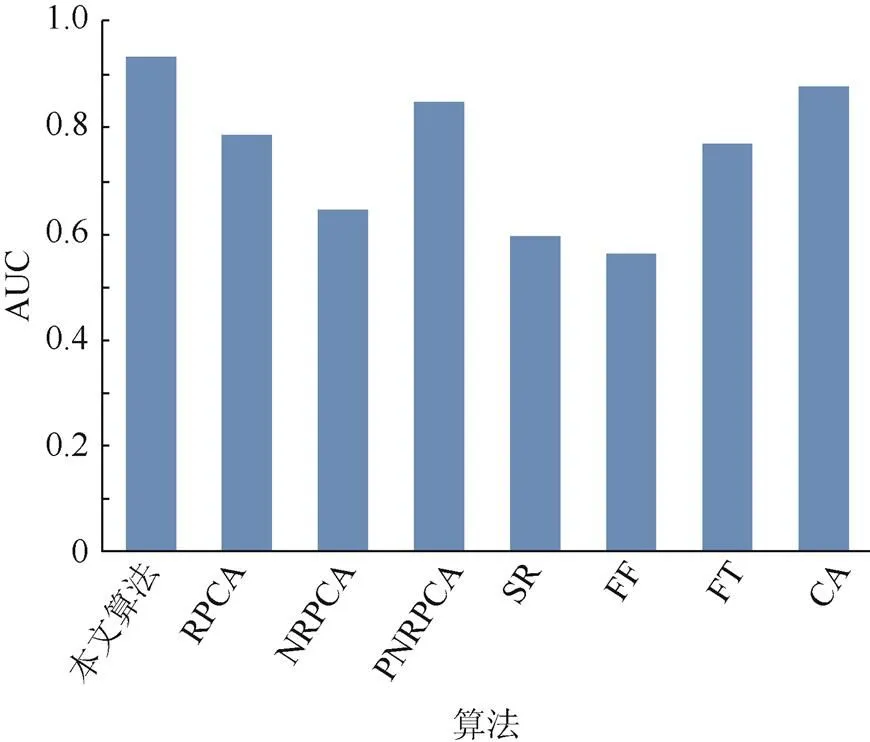
图7 各算法AUC图比较

3 结束语

本文结合视觉显著性检测和RPCA，提出了一种风机叶片表面缺陷的检测方法，通过在RPCA模型中增加F范数和Laplacian正则项，抑制光照不均和利用像素间的空间关系，实现风机叶片表面缺陷的检测。实验结果表明，本文算法对于风机叶片表面缺陷图像的检测具有较高的准确性。然而，由于本文算法在检测过程中，以超像素为基本的检测单元，而超像素分割对于微小缺陷的分割并不够理想，因此本算法在检测表面微小缺陷时，效果欠佳，这也是需要进一步研究的。

[1] Kumar A. Computer-vision-based fabric defect detection: A survey [J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 348-363.

[2] CandÈs E J, Li X D, Ma Y, et al. Robust principal component analysis? [J]. Journal of the ACM, 2011, 58(3): 1-37.

[3] 姚明海, 李洁, 王宪保. 基于RPCA的太阳能电池片表面缺陷检测[J]. 计算机学报, 2013, 36(9): 1943-1952.

[4] 李春雷, 高广帅, 刘洲峰, 等. 应用方向梯度直方图和低秩分解的织物疵点检测算法[J]. 纺织学报, 2017, 38(3): 149-154.

[5] Li C L, Liu C D, Gao G S, et al. Robust low-rank decomposition of multi-channel feature matrices for fabric defect detection [EB/OL]. Multimedia Tools and Applications. (2018-08-09) [2018-12-26]. https://doi.org/ 10.1007/s11042-018-6483-6.

[6] 钱晓亮, 张鹤庆, 张焕龙, 等. 基于视觉显著性的太阳能电池片表面缺陷检测[J]. 仪器仪表学报, 2017, 38(7): 1570-1578.

[7] 亢洁, 潘思璐, 王晓东. 基于RPCA的纸病图像分割算法[J]. 中国造纸学报, 2017, 32(2): 39-44.

[8] 王辉, 孙洪. 鲁棒主成分分析的铝箔表面缺陷检测方法[J]. 信号处理, 2017, 33(4): 577-582.

[9] Cen Y G, Zhao R Z, Cen L H, et al. Defect inspection for TFT-LCD images based on the low-rank matrix reconstruction [J]. Neurocomputing, 2015, 149: 1206-1215.

[10] Cao J J, Wang N N, Zhang J, et al. Detection of varied defects in diverse fabric images via modified RPCA with noise term and defect prior [J]. International Journal of Clothing Science and Technology, 2016, 28(4): 516-529.

[11] Cao J J, Zhang J, Wen Z J, et al. Fabric defect inspection using prior knowledge guided least squares regression [J]. Multimedia Tools and Applications, 2017, 76(3): 4141-4157.

[12] Achanta R, Shaji A, Smith K, et al. SLIC superpixels compared to state-of-the-art superpixel methods [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282.

[13] LinZ C, Chen M M, Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices [R]. Champaign: University of Illinois-Urbana-Champaign, 2009.

[14] Zhu W J, Liang S, Wei Y C, et al. Saliency optimization from robust background detection [C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2014: 2814-2821.

[15] Hou X D, Zhang L Q. Saliency detection: A spectral residual approach [C]//2007 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2007: 1-8.

[16] 李富生, 李霞, 陈宇. 基于改进四元傅里叶变换的显著性检测及其视频编码应用[J]. 计算机应用研究, 2015, 32(5): 1540-1545.

[17] Achanta R, Hemami S, Estrada F, et al. Frequency-tuned salient region detection [C]//2009 IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2009: 1597-1604.

[18] Goferman S, Zelnik-Manor L, Tal A. Context-aware saliency detection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(10): 1915-1926.

Surface Defect Detection of Wind Turbine Blades Based on RPCA and Visual Saliency

CAO Jin-gang1, YANG Guo-tian2, YANG Xi-yun2

(1. School of Control and Computer Engineering, North China Electric Power University, Baoding Hebei 071003, China; 2. School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)

Aiming at the problem of surface defect detection of wind turbine blades, a method based on robust principal component analysis (RPCA) and visual saliency is proposed. Based on RPCA, the method adds the noise term and Laplacian regularization term to facilitate the segmentation of defect images, that is, suppressing Gaussian noise and uneven illumination by F-norm regularization term, and constraining the spatial relationship of pixels with Laplacian regularization term which can preserve invariance and the local consistency among the spatially adjacent sub-regions with similar saliency values in a saliency map. Firstly, superpixel segmentation and feature extraction are performed on the surface image of input wind turbine blades to obtain the feature matrix of the image. Then, the sparse matrix is obtained by the improved PRCA, and the saliency map of the defect region is calculated according to the sparse matrix and visual saliency method. Finally, the saliency map is optimized and the adaptive threshold segmentation algorithm is used to detect defects. Through experimental simulation, the experimental results are qualitatively and quantitatively analyzed, which indicates that the proposed method has high detection accuracy.

RPCA; visual saliency; defect detection; wind turbine blades

TP 391

10.11996/JG.j.2095-302X.2019040704

A

2095-302X(2019)04-0704-07

2018-12-29；

定稿日期：2019-01-17

中央高校基本科研业务费专项资金(2018MS072)

曹锦纲(1981-)，男，湖北宜昌人，讲师，博士研究生。主要研究方向为智能系统与模式识别、计算机视觉等。E-mail：caojg168@126.com

杨国田(1962-)，男，辽宁义县人，教授，博士，博士生导师。主要研究方向为人工智能与模式识别等。E-mail：ygt@ncepu.edu.cn