基于直觉模糊集的防空作战目标威胁评估
陈德江,王 君
(空军工程大学防空反导学院,陕西 西安 710051)
0 引言
按照JDL信息融合功能模型,威胁评估(Threat Assessment,TA)处于第三级,属于高级的处理阶段。其功能是推测敌方武器装备对我方构成的威胁程度,推理敌方的兵力部署和行动意图。作为防空方,对不同目标做出正确的威胁评判,对于火力分配、辅助决策具有十分重要的意义。
目前常用的威胁评估理论或方法众多,主要有:直觉模糊集理论[1-5]、云模型理论[6]、多属性决策方法[7]、D-S证据理论[8]、贝叶斯推理[9]、TOPSIS法[10]等。文献[2]运用TOPSIS法来衡量直觉模糊集的相似性,得出最终的目标威胁排序;文献[3]提出了一种基于直觉模糊集的威胁评估模型;文献[4]通过改进有序加权平均算子(OWA),构建了新的直觉模糊集排序模型;文献[5]构造了不同形式的直觉模糊熵,并将其用于多属性决策等等。虽然上述方法各有优势,但尚存在如下不足:一是在确定目标威胁因素权重时,往往采用单一理论,难免导致主、客观权重的失衡;二是在评估准则的选取上,注重了目标威胁的“客观性”,忽略了决策者的主观偏好。因此,本文提出一种基于直觉模糊集的防空作战目标威胁评估方法。
1 评估指标体系及指标权重的确定
1.1 直觉模糊集相关基础知识
直觉模糊集[11](Intuitionistic Fuzzy Set, IFS)是对Zadeh模糊集的一种重要的扩展。Zadeh模糊集包含了支持x的证据μA(x),也包含了反对x的证据1-μA(x),但它不可能表示既不支持也不反对的“非此非彼”中立状态的证据。而一个直觉模糊集的隶属度μA(x)、非隶属度υA(x)以及直觉指数πA(x)则分别表示对象x属于直觉模糊集A的支持、反对、中立这三种证据的程度。因而引入直觉模糊集能够更好描述、处理威胁评估中的不确定性。Atanassov对直觉模糊集给出了如下定义:
设X是一个给定论域,则X上的一个直觉模糊集A为:
A={〈x,μA(x),υA(x)〉|x∈X}
(1)
式(1)中,μA(x):X→[0,1]和υA(x):X→[0,1]分别代表A的隶属函数μA(x)和非隶属函数υA(x),且对于A上的所有x∈X,0≤μA(x)+υA(x)≤1成立。直觉模糊集A可以简记为A=〈x,μA,υA〉或A=〈μA,υA〉/x。对于X中的每一个直觉模糊子集,称πA(x)=1-μA(x)-υA(x)为A中x的直觉指数(Intuitionistic Index),它是x对A的犹豫程度(Hesitancy Degree)的一种测度。
模糊熵是用来描述模糊集的模糊性和信息量的。若称函数E:IFS(X)→[0,1]为IFS集的直觉模糊熵(Intuitionistic Fuzzy Entropy,IFE),则需满足下列条件:
1)E(A)=0,当且仅当A为非模糊集;
2)E(A)=1,当且仅当∀x∈X,有μA(x)=υA(x);
3)E(A)=E(AC),∀A∈IFS(X);
4)对于IFS集A和B,若∀x∈X有:

1.2 目标威胁评估指标体系的构建
防空作战威胁评估是一个典型的多属性决策过程。来袭目标影响威胁程度的因素众多,本文主要考察以下几点:目标类型、目标与雷达的径向距离、目标高度、目标速度、航向角以及目标干扰能力。
各属性指标是通过其指标值的大小来影响评估结果的,但这些指标值的类型各异。如:目标类型、高度、距离及航向角为成本型指标(越小越好型),目标速度和干扰能力为效益型指标(越大越好型);同时,目标类型和干扰能力又属于定性指标,而目标高度、速度、距离和航向角属于定量指标。
1.3 各指标因素的规范化处理
指标值的规范化处理过程包括指标类型的一致化和指标值无量纲化。指标类型一致化是指将指标集中的所有的成本型指标转化为效益型指标,或将所有的效益型指标转化为成本型指标;指标值无量纲化是为了使得各指标值具有可比性,将其变换到某一取值范围,通常为[0,1]区间。用数学语言可将指标值xij的规范化过程描述为:
yij=φ2(φ1(xij))
(2)
式(2)中,xij表示第i个目标第j个属性的指标值;yij表示第i个目标第j个属性的规范化指标值;φ1和φ2分别是指标类型一致化方法、指标值无量纲化方法,可根据实际威胁评估问题的具体特点选取。
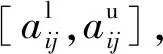
将上述获取的区间属性度量值进行规范化处理,可转化为直觉模糊判断矩阵[rij]m×n=[〈μij,υij〉]m×n,进而更好地描述目标属性值的变化过程。具体的规范化处理过程如下所示:
(3)
式(3)中,i表示第i个目标,i=1,2,…,m;j表示第j个属性,j=1,2,…,n;μij表示第i个目标第j个属性的威胁隶属度,υij表示第i个目标第j个属性的威胁非隶属度;C={Cj|j=1,2,…,n}=Cb∪Cc为完备指标集,Cb表示效益型指标集,Cc表示成本型指标集。
1.4 目标属性权重的确定
本节引入直觉模糊熵(IFE)来度量直觉模糊集的不确定性信息,建立一种基于熵最小化的非线性规划模型来求取目标属性的客观权重。基本步骤如下:
步骤1 确定目标属性的直觉模糊决策矩阵。
F=(fij)m×n
(4)
式(4)中,fij=(〈μij,υij〉);μij≥0,μij表示第i个目标归于第j个属性的隶属度;υij≥0,υij表示第i个目标归于第j个属性的非隶属度。
步骤2 计算第j个目标属性的直觉模糊熵。
(5)
步骤3 建立基于IFE的目标属性权重确定的非线性规划模型。
(6)
步骤4 求解目标属性客观权重ω1。对式(6)建立Lagrange函数:
(7)
分别对ωj1和λ求导,并令其等于0,则有:
(8)
解得:
(9)
由于基于IFE方法求出的是目标属性的客观权重,为兼顾决策者的主观偏好,考虑运用层次分析法(AHP)或专家调查法求取目标属性的主观权重ωj2(由于篇幅原因,具体求解过程略去)从而对上述客观权重ωj1进行主观修正。
(10)
式(10)中,ωj1表示第j个目标属性的客观权重,ωj2表示第j个目标属性的主观权重,σ1、σ2为加权系数,且σ1+σ2=1。则修正后的目标属性综合权重为ω=(ω1,ω2,…,ωn)。
2 基于直觉模糊集的防空作战目标威胁评估模型
2.1 基于直觉模糊集的TOPSIS
逼近理想解排序法(TOPSIS)的核心思想是:通过比较各序列与正、负理想解序列之间的欧式距离做出决策,即越接近正理想序列,越远离负理想序列的方案越佳。下面求解目标集属性序列到正、负理想解序列的欧式距离:
步骤1 根据式(4)确定直觉模糊决策矩阵F。
步骤2 计算加权直觉模糊决策矩阵:
R=(〈αij,βij〉)m×n
(11)
式(11)中,〈αij,βij〉=ωj〈μij,υij〉=〈1-(1-μij)ωj,(υij)ωj〉,〈αij,βij〉表示决策矩阵F的第i个目标第j个属性的直觉模糊度量值。
步骤3 计算矩阵R的正、负理想解序列,分别记作R0+(j)和R0-(j)。其中R0+(j)=[R0j+|j=1,2,…,n],R0-(j)=[R0j-|j=1,2,…,n]。
正理想解序列为:
R0+(j)=(〈α1+,β1+〉,〈α2+,β2+〉,…,〈αn+,βn+〉)
(12)
针对效益型指标和成本性指标有:
负理想解序列为:
R0-(j)=(〈α1-,β1-〉,〈α2-,β2-〉,…,〈αn-,βn-〉)
(13)
针对效益型指标和成本性指标有:
步骤4 求解目标集属性序列到正、负理想解序列的欧式距离。
到正理想解序列R0+的欧式距离为:
(14)
到负理想解序列R0-的欧式距离为:
(15)
2.2 基于直觉模糊集的灰色关联算法
灰色关联法的核心思想是通过比较序列曲线几何形状的相似程度来判断其关联程度,即曲线越接近,相似度越高,相应序列之间的关联度越大,反之则越小。由于对直觉模糊集序列进行分析,传统的灰色关联模型无能为力,故而提出一种基于直觉模糊集的灰色关联模型。
根据文献[12]的灰色关联四公理,则可推理得出目标集的属性序列与正、负理想序列间的灰色关联系数:
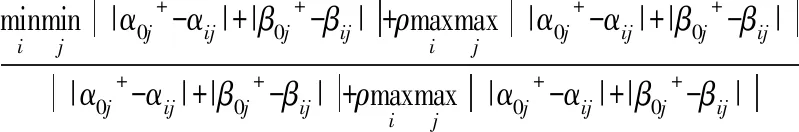
(16)

(17)
式(16)、式(17)中,ρ为分辨系数,一般取ρ=0.5。则相应的正、负关联度如下:
(18)
(19)
式(18)、式(19)中,ξi+(j)、ξi-(j)分别表示目标i对属性j的正、负关联系数,γi+、γi-分别表示目标i的正、负关联度。
2.3 基于偏好系数的目标威胁排序
文献[3]仅考察了序列间的距离关系,文献[8]仅考察了序列间的灰色关联度。针对传统的威胁评估方法忽视了决策者的偏好对于威胁排序的影响,本节提出了一种基于偏好系数的目标威胁排序模型。由于Di-、γi+的值越大,目标的威胁程度越大;Di+、γi-的值越小,目标的威胁程度越小。则目标威胁度的正、负贴近度可表示为:
Si+=λ1·γi++λ2·Di-
(20)
Si-=λ1·γi-+λ2·Di+
(21)
式(20)、式(21)中,λ1+λ2=1,λ1为偏好系数,可以反映决策者对γi和Di的偏好程度。采用归一化形式,建立威胁排序函数,求取目标的最终威胁度:
(22)
通过比较威胁度Ci的大小,可得到最终各目标的威胁度排序结果。特别的,当λ1=1,λ2=0时,评估模型退化为灰色关联模型,当λ1=0,λ2=1时,评估模型退化为TOPSIS模型,当λ1,λ2∈(0,1)时,若λ1>λ2,则表示决策者偏好于曲线几何形状对威胁评估的影响,若λ1<λ2,则表示决策者偏好于欧式距离对威胁评估的影响。
2.4 算法流程
步骤1 针对评估指标体系,运用1.2节中所介绍的方法,将定性、定量属性进行规范化处理,确定直觉模糊决策矩阵F;
步骤2 由式(4)—式(10)求取目标属性综合权重ω;
步骤3 构造加权直觉模糊决策矩阵R;
步骤4 由式(12)、式(13)确定正、负理想解序列R0+(j)和R0-(j);
步骤5 由式(14)—式(19)求取目标序列与正、负理想序列间的欧式距离Di+、Di-以及正、负灰色关联度γi+、γi-;
步骤6 根据偏好系数λ1的取值,由式(20)、(21)求取目标的正、负贴近度Si+、Si-;
步骤7 由式(22)求取各目标的最终威胁度Ci,得到目标集的最终威胁排序。
3 仿真校验
假定有5批目标同时对我方要地进行空袭,由于不同传感器的性能差异和作战环境因素的影响,在时刻t~t+Δt内获取的各目标属性的测量值为区间值,设目标集为{A1,A2,…,A5},目标属性集为{M1,M2,…,M6}。如表1所示。
根据由1.2小节中介绍的方法,针对定性指标,其直觉模糊度量值由专家给出,针对定量的目标属性,其直觉模糊度量值可运用式(3)求得。从而,得到经规范化处理后的直觉模糊决策矩阵F,如式(23)所示。根据决策矩阵以及评估指标体系,结合式(4)—式(10),计算可得到各目标属性的主、客观综合权重为ω=(0.32,0.20,0.17,0.13,0.10,0.08)。由式(11)构造直觉模糊加权决策矩阵R,由式(12)、式(13)可得到目标属性的正、负理想序列,其结果如表2所示。

(23)

表1 t~t+Δt时刻来袭目标属性测量值

表2 直觉模糊加权决策表及正、负理想序列
由式(14)—式(19)可求解得到目标集属性序列到正、负理想序列的欧式距离和正、负灰色关联度。运算结果如表3所示。

表3 欧式距离及正、负关联度
根据偏好系数λ1的取值不同,反映出的决策者对序列曲线形状(灰色关联度)和位置关系(欧式距离)间的偏好程度,根据不同的λ1取值,利用威胁排序函数,则可求出各目标归一化后的威胁度,进而对上述5批来袭目标进行威胁排序。不妨分别取偏好系数λ1=(0.0,0.2,0.5,0.8,1.0)加以分析,其仿真结果如表4所示。
表4给出了在5种不同偏好系数下的仿真结果,可得到:当λ1=0.0时,来袭5批目标的最终威胁排序结果为A3>A2>A1>A4>A5,此时,对目标威胁排序的思想为基于IFS的TOPSIS算法,与文献[3]结论相同;当λ1=0.2时,有A3>A2>A1>A5>A4,从图1中可明显看出,在λ1∈(0.1,0.2)中,目标4和目标5的威胁排序位置发生一次交换;当λ1=0.5时,有A3>A2>A5>A1>A4,在λ1∈(0.3,0.4)中,目标1与目标5的威胁排序位置交换一次;当λ1=0.8,λ1=1.0时,有A3>A2>A5>A4>A1,在λ1∈(0.6,0.7)中,目标1与目标4的威胁排序位置交换一次,且λ1=1.0时,对目标威胁排序的思想为基于IFS的灰色关联算法,与文献[12]结论相同。在整个评估过程中,目标3的威胁度最大、目标2其次,在两种评估思想下均保持不变,验证了评估算法的稳定性;而随着偏好系数λ1的变化,目标1、目标4、目标5的威胁度发生变化,进而改变其对应的威胁排序位置,表明了算法的灵活性。

表4 各目标威胁度及其威胁排序结果

图1 目标威胁度随λ1的变化曲线Fig.1 The curve of target threat degree with λ1
进一步分析本算法可知,对于序列间灰色关联度和欧式距离的倾向程度,可根据不同的偏好系数进行调整,当λ1=0时,评估算法为基于IFS的TOPSIS算法;当λ1=1时,评估算法为基于IFS的灰色关联法;当λ1∈(0,1)时,评估算法灵活的调整于二者之间。因而,本算法克服了文献[3,12]中评估理论单一性的不足,使得算法具有更强的灵活性和普适性。
4 结论
本文提出了基于直觉模糊集的防空作战目标威胁评估方法,该方法通过基于IFE的非线性规划模型和AHP法求取能够反映目标属性主客观信息的综合权重,在考虑决策者偏好程度的基础上,将TOPSIS模型和灰色关联模型有机结合,建立了目标威胁排序函数。仿真结果表明,调整偏好系数λ1,可分配序列间的位置关系(欧式距离)和序列曲线几何形状(灰色关联度)对评估结果的影响程度,并通过对比分析,验证了该方法的灵活性和可靠性,可为防空作战决策提供一定的理论依据。

