密集杂波下的模糊数据关联多目标跟踪算法
康旭超,何广军,陈 峰,何其芳
(空军工程大学防空反导学院,陕西 西安 710051)
0 引言
密集杂波环境下的多目标跟踪一直是目标跟踪领域的一个难题,雷达捕捉到的信号除了真实量测外还包括杂波引起的虚假量测,难以实现对目标的准确跟踪[1]。很多学者对于虚假目标与目标的区分已经做了很多研究,但都存在计算量大、区分目标复杂的问题,不利于目标的实时跟踪[2]。
在杂波环境下对目标进行跟踪的概率数据关联算法(PDA)计算量小,但在杂波密集的超低空环境下容易跟错目标。联合概率数据关联算法(JPDA)能够解决杂波密集环境下的目标跟踪,但随着目标数量的增加,算法计算量过大,不利于目标的实时跟踪[3]。文献[4]通过模糊聚类得到每个测量点迹与目标预测位置之间的隶属度,并将其作为权值系数对有效回波的信息量进行加权,来实现目标的状态估计的更新,提高了跟踪的实时性,但密集杂波环境下多目标跟踪的准确性不佳。文献[5]在考虑到存在的公共量测对目标估计的影响,在模糊聚类的基础上加入了尺度因子,并根据目标群的位置信息以及运动方向信息进行多级聚类,一定程度上提高了目标跟踪的准确性,但并未考虑多目标在近距离和远距离情况下公共量测对于目标估计的影响权重的不同,影响跟踪精度。本文针对此问题,提出了密集杂波下的模糊数据关联多目标跟踪算法。
1 密集杂波下的多目标跟踪问题
1.1 问题描述
假设在多目标跟踪系统中,有C个跟踪目标,在k时刻目标i(1,2,3,…,M)的运动状态方程为:
(1)
假设k时刻目标i的观测方程为:
(2)
本文解决的问题是在某时刻k测得n个观测量Zk(j)(j=1,2,…,n),观测量中包含密集杂波(虚假目标),在无法区分杂波与真实目标量测的前提下,利用模糊聚类的思想对每个观测量(包含杂波)进行聚类[6],得到每个观测量相对于目标的隶属度作为模糊关联概率,分析远近距离两种情况下公共量测对目标的影响,引入影响因子重建模糊关联概率矩阵,然后结合卡尔曼滤波的方法对不同观测量的状态估计进行加权融合得到下一时刻目标的估计状态,通过对目标轨迹进行单独的估计从而实现对超低空多目标的实时跟踪。
1.2 模糊C均值聚类
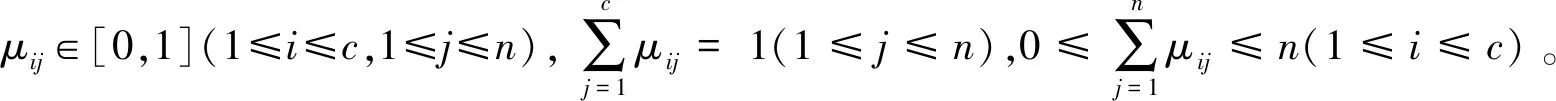
模糊划分矩阵U=(μij)c×n,定义模糊函数:
(3)
式(3)中,dij为样本j与目标i之间的欧氏距离‖zj-vi‖,vi表示目标i的聚类中心,m表示模糊指数,满足1≤m≤。
利用最小化目标函数完成模糊分类,具体流程如下:
1) 确定目标C,以下一时刻状态预测值作为初始聚类中心,选择合适的模糊指数m,从聚类有效性试验研究中得到m的最佳取值范围为[1.5 2.5],通常取m=2,给定迭代停止阈值ε。
2) 初始化隶属度矩阵U,计算各个数据到聚类中心的距离dij,计算隶属度矩阵,t=0。
3) 更新隶属函数矩阵U=(μij)c×n。
其中,
(4)
4) 更新聚类中心
(5)
5) 若|vi(t)-vi(t+1)|<ε,迭代结束,得到模糊划分矩阵,否则转到步骤3)。
本文中,在目标数(聚类数)已知的前提下,以下一时刻目标的预测位置为聚类中心,以各量测与聚类中心的欧氏距离为测度计算量测对于目标的隶属度。
2 密集杂波下的模糊数据关联多目标跟踪算法
2.1 模糊数据关联方法
建立目标椭圆跟踪门,确认各目标有效观测距离ri,‖ri‖≤τi减少野值。其中τi为目标i的观测阈值。
1) 建立量测归属矩阵Λ:
(6)
式(6)中,
(7)
ϑ11=1表示观测量z1落入目标1的跟踪门,ϑ23=0表示观测量z3没有落入目标2的跟踪门。
图1中▲表示目标的预测位置,以目标预测位置为中心建立跟踪门,●表示某一时刻量测点(包含杂波与真实目标量测),假设某一时刻,目标只有一个真实量测,其余为杂波引起的虚假量测,跟踪门重叠区域的量测为公共量测。
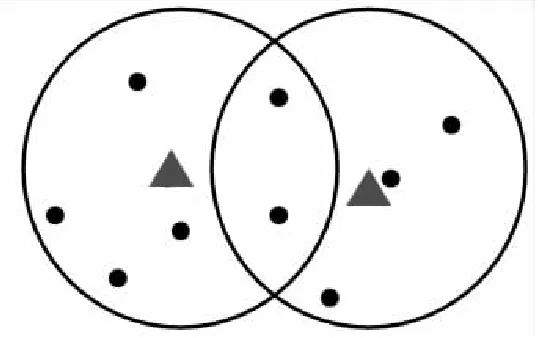
图1 目标确认区域的量测值分布Fig.1 Distribution of measurements in target recognition area
传统算法中大多未考虑多目标跟踪门出现重合,即存在公共量测的情况[4]。虽然有学者考虑到存在公共量测时公共量测对目标估计的影响,但未考虑多目标在距离较近和较远的情况下公共量测对于目标估计影响权重的变化,影响跟踪的精确性[11]。改进的模糊聚类关联算法通过对多目标远近距离下公共量测对于目标估计的影响权重的不同进行了分析,在远近两种情况下实时调整公共量测的权重。
对于两个相距较远的目标,认为公共量测区域量测值为目标真实观测的概率很小,通常认其为杂波,此时引入尺度因子来降低公共量测对于目标估计的权重。但两个目标相距较近时,尤其是进行交叉时,非公共量测为杂波的可能性更大,此时应该引入尺度因子降低非公共量测的权重。
当目标距离较远时量测分布如图2所示。
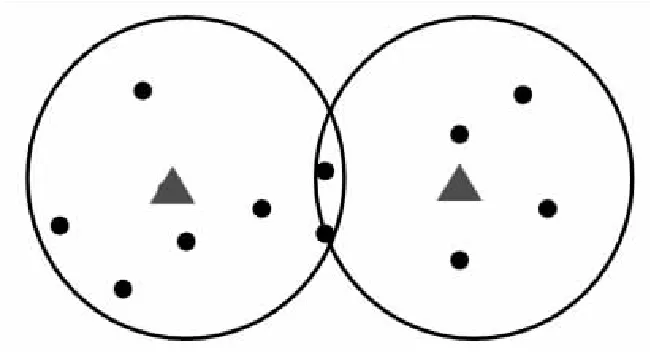
图2 目标相距较远时量测分布Fig.2 Distribution of measurements when targets are far apart
此时公共量测与目标预测的偏差较大,为杂波的可能性较高,引入影响因子降低公共量测的权重。
当目标距离较近时量测分布如图3所示。
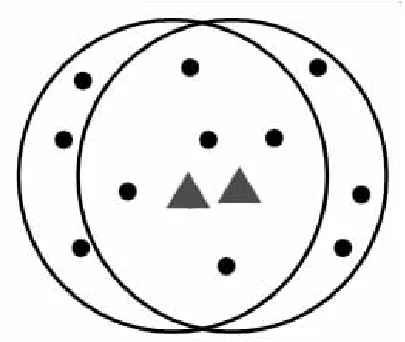
图3 目标相距较近时量测分布Fig.3 Measurement distribution when the target is close to each other
此时非公共量测与目标预测的偏差较大,为杂波的可能性较高,引入影响因子降低非公共量测的权重。
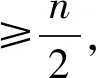
(8)
引入影响因子ζpub降低公共量测的权重
(9)
ϑij*=ζpubϑij
(10)
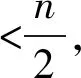
非公共量测集合
(11)
引入影响因子ζnonpub降低非公共量测的权重
(12)
ϑij*=ζnonpubϑij
(13)
引入影响因子后的量测分布矩阵:
(14)
2) 建立量测权值矩阵Π
(15)
式(15)中,ωij=ϑij*μij。
2.2 结合模糊聚类关联的多目标跟踪算法
利用FCM算法得到量测权值矩阵U,结合卡尔曼滤波,针对杂波环境下量测的不确定性利用联合关联信息对目标进行单独的跟踪。其具体流程如下:
步骤2 预测下一时刻目标状态,作为下一时刻的聚类中心。
(16)
步骤3 观测预测。
(17)
步骤4 确定各目标的有效观测,最大观测范围ri,建立量测归属矩阵Λ。
步骤5 利用模糊聚类计算各量z(j)测属于目标i的隶属度关系矩阵U=(μij)c×n。
步骤6 根据公共量测数与总量测数的关系引入尺度因子ζpub,ζnonpub,建立量测权值矩阵Π。
步骤7 一步预测均方误差。
Pi(k/k-1)=Fi(k/k-1)Pi(k-1)·
Fi(k/k-1)T+Qi(k-1)
(18)
步骤8 计算滤波增益。
Ki(k)=Pi(k/k-1)Hi(k)T(Hi(k)·
Pi(k/k-1)Hi(k)T+Ri(k))-1
(19)
步骤9 利用不同量测相对目标的权值作加权融合,得到第i个目标的状态更新值。
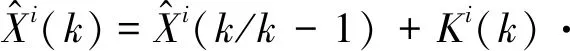
(20)
步骤10 估计均方误差。
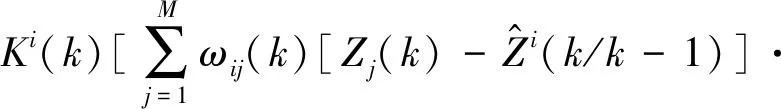
(21)
3 仿真结果与分析
传统多目标跟踪算法未考虑公共量测对估计精度的影响[4],本文算法在此基础上引入公共量测影响因子,调整公共量测权重,进一步提升密集杂波下多目标跟踪性能。
分别对2个匀速直线运动的目标建立目标状态方程:
X(k+1)=FX(k)+Gw(k)
(22)
观测方程为:
Z(k)=HX(k)+v(k)
(23)
式(23)中,
为了检验算法的可靠性,设置了两个场景:
场景1 检验两个目标距离较远(不存在交叉)时算法的可靠性。
假设有2个匀速直线运动的目标,目标1、目标2的初始位置分别为(1 500,4 000),(1 000,900),目标1水平速度分别为300 m/s,垂直方向上的速度为200 m/s,目标2水平速度分别为200 m/s,垂直方向上的速度为100 m/s,采样周期为0.2 s,隶属度矩阵U的指数设为2,最大迭代次数设为100,迭代终止条件隶属度最小变化量为1×10-5。目标真实运动轨迹如图4所示。
在杂波较为稀疏的情况下,取杂波系数λ=2时,目标跟踪轨迹及误差曲线如图5、图6所示。
在杂波较为密集的情况下,取杂波系数λ=5时,目标跟踪轨迹及误差曲线如图7、图8所示。
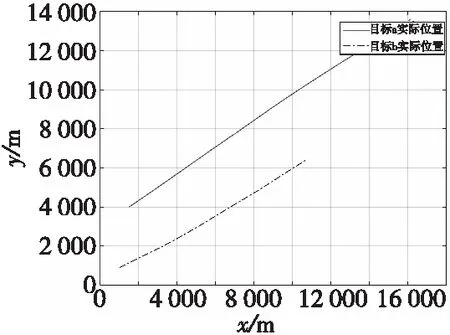
图4 目标真实运动轨迹Fig.4 The real trajectory of the target
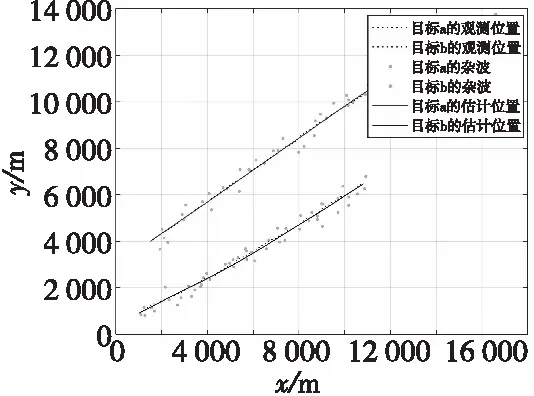
图5 目标跟踪轨迹Fig.5 Target tracking trajectory
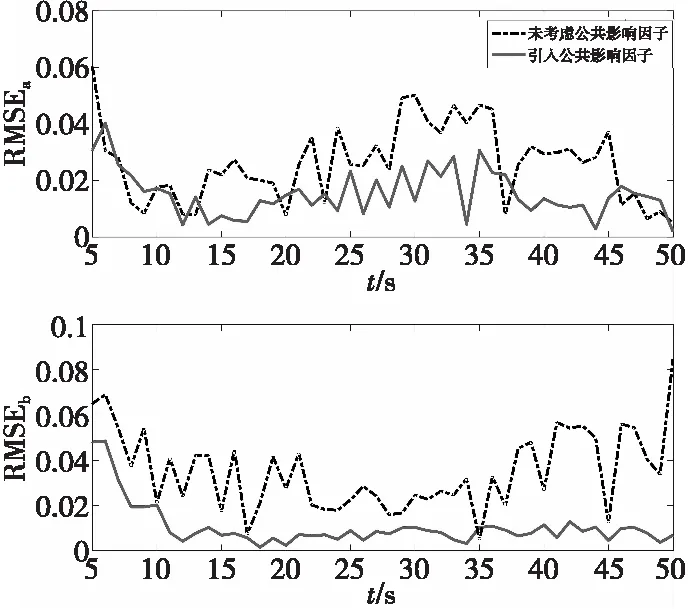
图6 目标a与b的误差曲线Fig.6 Error curves of targets a and b
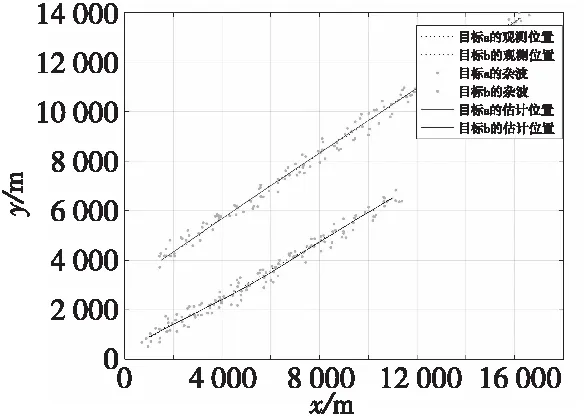
图7 密集杂波环境下目标跟踪轨迹Fig.7 Target tracking trajectory in dense clutter environment
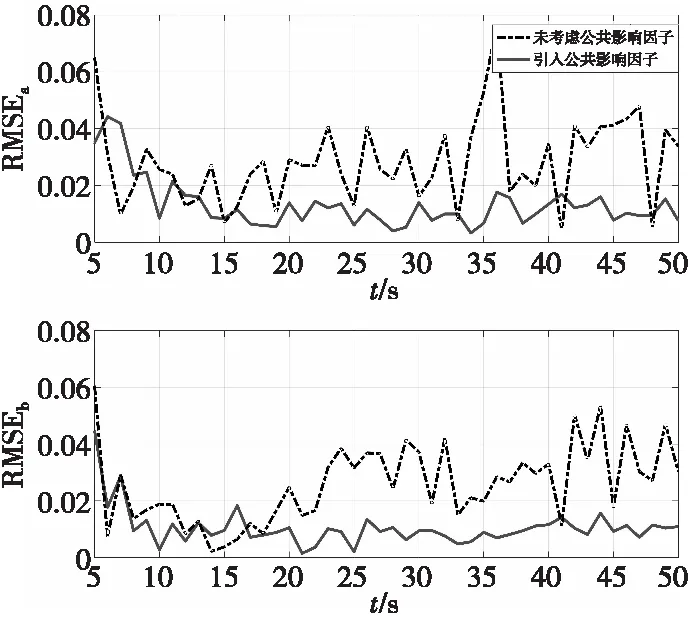
图8 密集杂波环境下目标a与b的误差曲线Fig.8 Error curves of target a and b in dense clutter environment
由仿真结果分析可知,当两目标距离较远时,对比未考虑公共影响因子的传统多目标跟踪算法,本文算法能够对目标进行更为精确的跟踪,误差基本控制在0.05以内。本文算法在传统算法的基础上通过对公共量测量的分析调整权重以提高估计精度,但由于在杂波相对较为稀疏的环境下公共量测较少,因此性能提升相对不明显。本文研究内容为杂波密集环境下多目标跟踪算法性能的提升,仿真结果证明在杂波密集环境下本文改进算法有较好的跟踪效果。
场景2 检验两个目标距离较近(存在交叉)时算法的可靠性。
假设有2个匀速直线运动的目标,目标1、目标2的初始位置分别为(1 500,1 000),(1 000,900),目标1水平速度分别为300 m/s,垂直方向上的速度为200 m/s,目标2水平速度分别为200 m/s,垂直方向上的速度为100 m/s,采样周期为0.2 s,隶属度矩阵U的指数设为2,最大迭代次数设为100,迭代终止条件隶属度最小变化量为1×10-5。目标真实运动轨迹如图9所示。
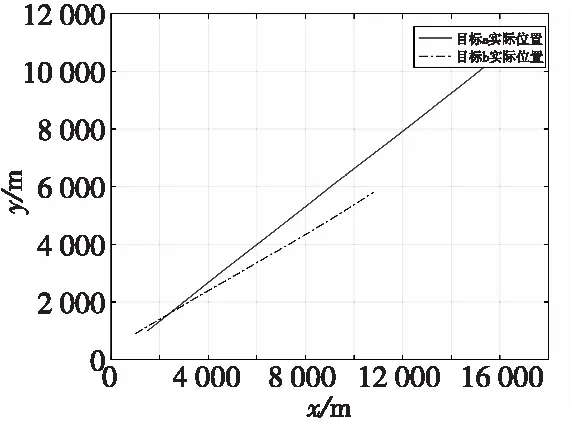
图9 目标真实运动轨迹Fig.9 Target real motion trajectory
在杂波较为稀疏的情况下,取杂波系数λ=2时,目标跟踪轨迹及误差曲线如图10、图11所示。
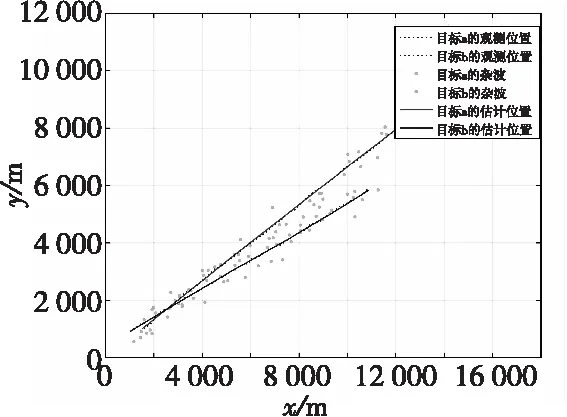
图10 目标跟踪轨迹Fig.10 Target tracking trajectory
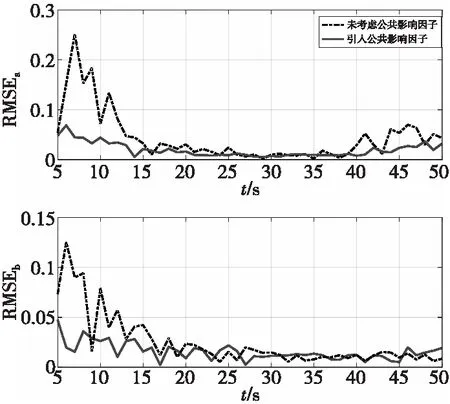
图11 目标a与b的误差曲线Fig.11 Error curves of targets a and b
在杂波较为密集的情况下,取λ=5时,目标跟踪轨迹及误差曲线如图12、图13所示。
由以上仿真结果可知,当两目标距离较近时,未考虑公共因子的传统算法有较大的误差,本文算法通过对公共影响因子权重的调整,使误差明显减小,误差波动也得到了明显的抑制。在杂波密集的情况下,杂波数增加,该算法依然能够对多目标稳定跟踪,误差控制在0.1之内,基本稳定在0.05附近。
通过对两种场景的仿真分析可得不论是对于近距离目标还是远距离目标,相较于未考虑公共影响因子的传统多目标跟踪算法,本文改进算法均能更为准确地反映目标的运动轨迹,且对于杂波密集下的多目标跟踪有较好的跟踪效果,证明了所提出的跟踪算法更适合对密集杂波干扰环境下的多目标进行跟踪。
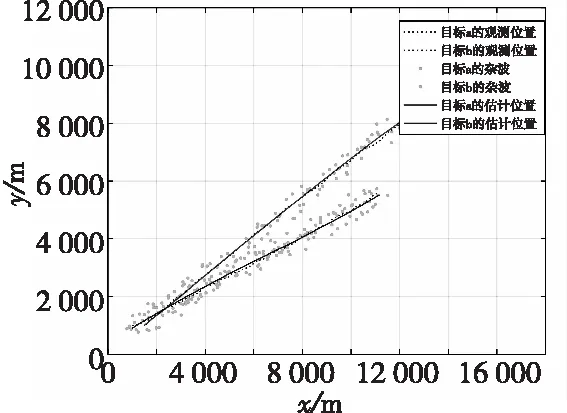
图12 密集杂波环境下目标跟踪轨迹Fig.12 Target tracking trajectory in dense clutter environment
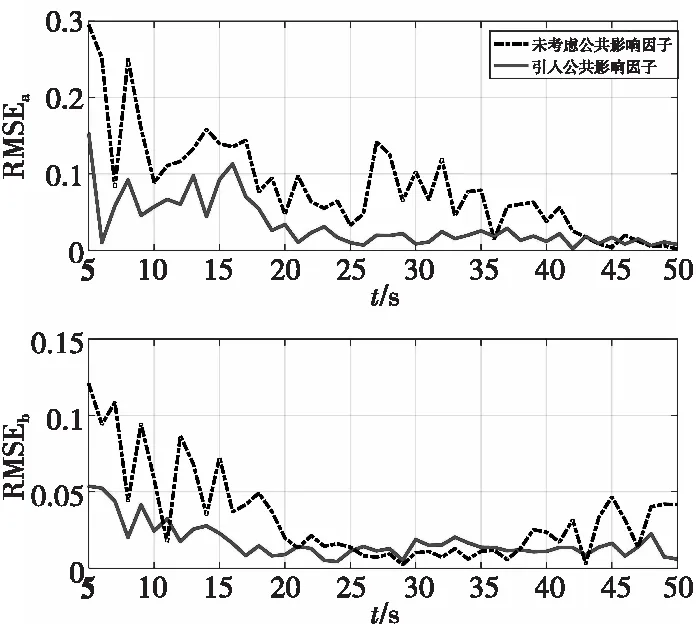
图13 密集杂波环境下目标a与b的误差曲线Fig.13 Error curves of target a and b in dense clutter environment
4 结论
本文提出密集杂波下的模糊数据关联多目标跟踪算法,该算法利用模糊聚类,得到不同观测量相对目标的隶属度作为模糊关联概率,引入远近距下的公共观测影响因子重建模糊关联概率矩阵,将重建后的模糊关联概率作为权值,结合卡尔曼滤波对某一时刻不同量测的状态估计加权融合作为目标的估计状态,实现目标的状态更新。仿真结果表明,在杂波密集的环境下,采用本文算法在能够保证目标跟踪实时性的同时引入远近距下公共观测影响因子对不同观测量的状态估计进行加权,保证了目标跟踪的准确性。

