传感器网络中的时变信号跟踪分布式估计器
马玉清 ,李 琳
(1.安徽工商职业学院信息工程学院,安徽 合肥 231131;2.上海理工大学光电信息与计算机工程学院, 上海 200093)
0 引言
由于对分布式、网络化和大规模系统的科学研究越来越深入和广泛,分布式估计算法已经成为非常有用的工具之一。事实上,由于一般传感器网络的功率、计算和通信能力有限,在不借助于集中式结构的情况下,每个节点能够估计一些信号的值是很重要的,例如,在监测大规模系统时,这尤其明显[1-3]。集中式解决方案需要数据融合中心,这种方法不但存在可扩展性问题,而且需要大量的能量和通信资源,更进一步的不利因素是非鲁棒性导致的故障;而分布式方法是可扩展的,每个节点仅使用本地信息,相邻节点间的协作大大提高了估计质量。
网络内(包括传感器网络)分布式估计算法是在分布式自适应滤波的背景下提出来的。在文献[4]以及其所引用的文献中,对于递归最小二乘和最小均方算法,提出了基于扩散和增量自适应解决方案。文献[5]针对节点服从广义系统模型的传感器网络系统,提出了分布式估计和融合算法;并基于线性最小方差准则导出了局部滤波估计器、一步预测估计器及其相应的估计误差互协方差矩阵;最后,基于矩阵加权线性最小方差最优融合准则,将局部估计值进行加权融合,得到融合Kalman滤波器和一步预测估计器。仿真结果表明融和滤波器精度高于单传感器局部滤波器。文献[6]研究了分布式协同信息处理技术在自适应目标参数估计问题中的应用,并基于自适应滤波算法,利用分布式策略进行目标参数协同估计,提出了一种无约束条件实时估计噪声方差的方法,并根据不同的分布式LMS算法,提出了分布式偏差补偿LMS算法。仿真结果表明,分布式偏差补偿LMS算法能够实现目标参数的无偏估计。在文献[7]中,针对受噪时变信号的分布式跟踪提出了一种最小方差估计器。文献[8]采用线性一致性算法对分布式估计和控制应用进行了研究。文献[9—10]基于卡尔曼滤波,提出了分布式状态估计的一致性算法。这种方法将扩散机制与分布式卡尔曼滤波[11]结合起来,将局部卡尔曼滤波器的估计值传递给相邻节点,然后用扩散策略求平均;在文献[12—13]中,通过采用连续卡尔曼一致滤波算法,提出了一种用于协同目标跟踪的移动传感器网络的分布式估计和移动控制的体系结构;在文献[14]中,对时变信号的分布式平均计算进行了分析,定义了一个凸优化问题来计算每个节点所使用的权值,以使估计值的最小均方偏差最小化。文献[15]研究了多个条件约束的凸优化子问题的解决方案的分布式估计,构造了一个最大似然估计器,采用乘数交替方向法并结合块坐标下降法对问题进行分解。文献[16]提出了一种利用移动水平估计概念的算法,假设所观察到的过程具有线性动态特性。分布式估计的另一种方法是基于非线性滤波,它采用自同步和耦合函数[17],每个节点的估计值是由一个合适的非线性动态系统的状态提供的,而这种系统是通过适当的静态耦合函数耦合到其他一些节点的。
上述各种估计器很少针对传感器网络中受噪时变信号进行跟踪估计,或者存在估计值结果差等缺陷,对此,本文针对传感器网络中时变信号的跟踪估计及这些估计器存在的不足,提出了新的分布式估计器。
1 问题构建及分析
1.1 问题构建
用diag(·)表示对角矩阵,即仅在对角线上有元素,用|·|表示求基数,用‖·‖表示求矩阵的谱范数。给定一个随机变量x,用Ex表示它的数学期望,用1和I分别表示向量(1,…,1)T和单位矩阵。
考虑N1个传感器节点,测量一个受加性噪声影响的标量信号d(t)得到:
ui(t)=d(t)+vi(t)i=1,…,N
(1)
式(1)中,vi(t)是零均值白噪声。由全部变量构成的向量可以写为:
u(t)=d(t)1+v(t)
(2)
假设v(t)的协方差矩阵Σ是对角的,为简单起见和不失一般性,选取Σ=2I,但结果在更一般和实际情况下也成立,即
把通信网络建模为一个无向图G=(V,E),其中Ni={jV:(j,i)E}{i}为节点iV的邻居加上节点i本身的集合,假设没有消息丢失。
每个节点i计算信号d(t)的一个估计值xi(t),采用相邻估计值和测量值的线性组合:
(3)
采用向量表示,上式变为:
x(t)=K(t)x(t-1)+H(t)u(t)
(4)
式(4)中,K(t)和H(t)可以看作是带有时变权值的2个图的邻接矩阵。算法用xj(0)=ui(0)(jNj)初始化。
估计误差e(t)=x(t)-d(t)1可以计算为:
e(t)=K(t)e(t-1)+d(t)(K(t)+H(t)-I)1-
δ(t)K(t)1+H(t)v(t)
(5)
式(5)中,δ(t)=d(t)-d(t-1)。估计误差动态性关于随机变量v(t)的期望值如下:
Ee(t)=K(t)Ee(t-1)+
d(t)(K(t)+H(t)-I)1-δ(t)K(t)1
(6)
假设1 假设(K(t)+H(t))1=1。
假设1是保证集中式估计误差的收敛性的,是由Speranzon等得出的[7],而且在本文的情况下也同样成立。另外,如果H(t)1=1,则估计误差的期望值收敛到0,因而估计误差是无偏的;否则,如果d(t)是慢时变的(也就是δ(t)是有界的),那么‖Ee(t)‖在原点的邻域上也趋于有界值。这样,如果考虑第i个节点,则估计误差的期望值可以以分布式方式计算如下:
(7)
式(7)中,εi(t)为收集节点i上的可用估计误差,并根据它们的指标排序:
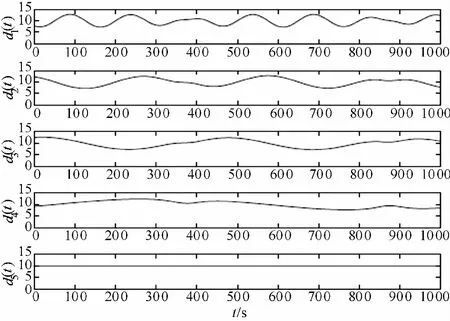
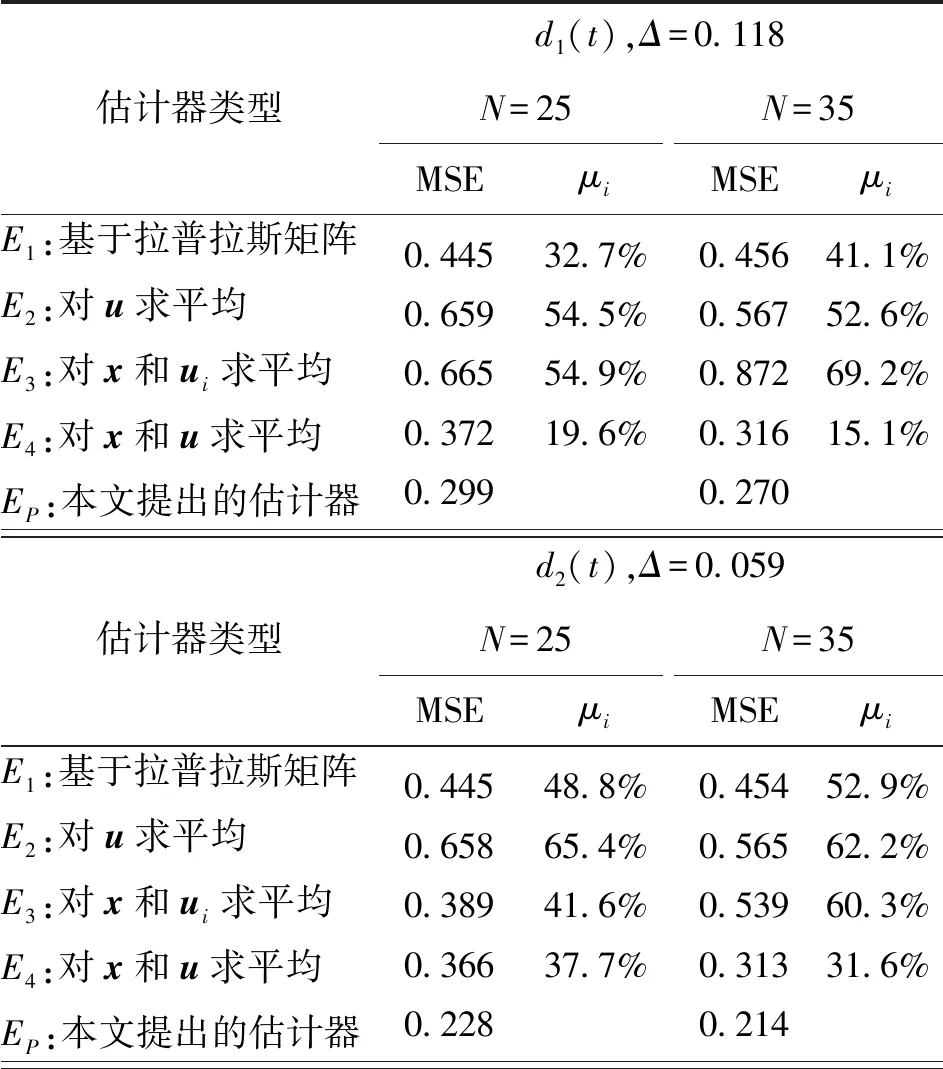
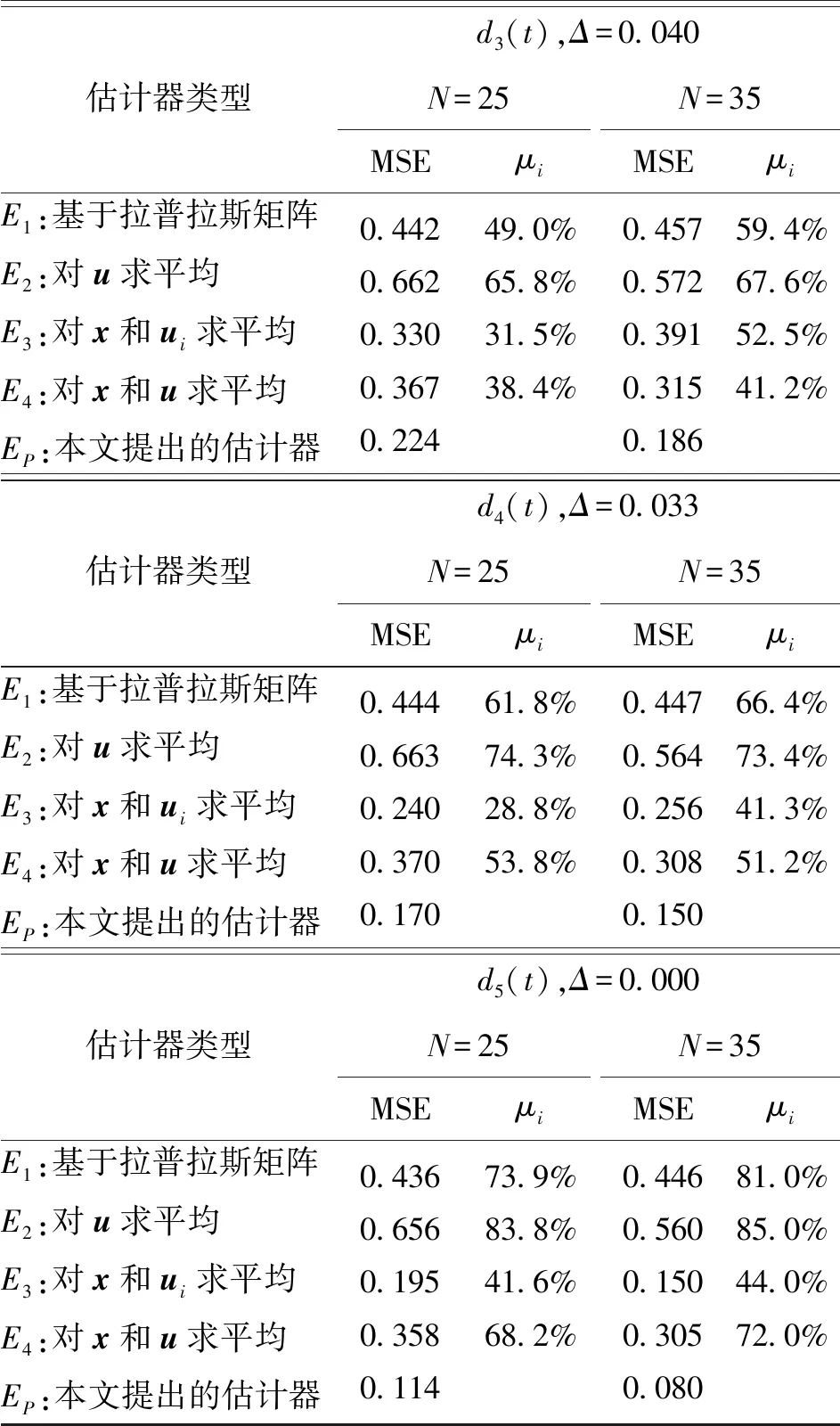
εi=(ei1,…,eiMi)Ti1<… (8) (9) (10) 式(10)中,0≤ρi≤1,P1=Eei(t)是估计误差的偏差项,P2=E(ei(t)-Eei(t))2是估计误差的方差项。这个问题可以通过每个节点i以分布式方式求解。把它重写为: (11) 式(11)中, (12) 命题1.1:对于一个给定的正定矩阵Θi(t),该最优化问题的解为: (13) (14) 证明:因为这个问题是凸的,且Slater条件成立,则Karush-Kuhn-Tucker(KKT)条件对于最优化是充分必要条件: (15) (16) 只需求解由KKT条件所确定的方程组,就可以得到闭形式的解。 (17) 值得注意的是,如果将Pareto参数设置为ρi=1,结果表明只有偏差被最小化,而最优成本函数为: (18) 如果将Pareto参数设置为ρi=0,结果表明方差被最小化,最优成本函数为: (19) 显然,帕累托参数可以基于所需的特点来设置。下一节将表明如何通过适当设置这个参数来确定偏差的界限。 通过定义下列全局约束条件,就可以确定偏差界限: γmax(K(t))≤f(Δ,γ) (20) 式(20)中,γmax(K(t))表示矩阵K(t)的最大奇异值,γ表示信噪比,Δ是信号导数的上界,且: (21) 当下列局部约束条件成立时,这个全局约束条件就成立: ‖κi‖2≤ψi (22) 式(22)中,ψi0是一个合适的常数标量,可以进行局部计算[7]。这个新的约束条件确保估计误差的稳定性,即使它在一般情况下得到一个与集中式解不同的分布式解。考虑到偏差界限,问题(11)可以重新构建如下: (23) (24) 式(24)中最后两个条件是从拉格朗日算子得到的: (25) 通过将这两个KKT条件与第二个条件相结合,就得到最优值: (26) (27) (28) 而且通过选取 (29) 第四个KKT条件就是满足的。可以看到,通过设置一个合适的帕累托参数ρi值,并保持式(13)和式(14)的结果,就可以对偏差确定一个合适的界限。 现在来分析如何实现估计器。本文考虑信号是分量方向准平稳的。由于式(4)的时变线性系统是一致有界输入-有界输出稳定的,则x(t)也是准平稳的,因此均值Eεi=mεi(t)和协方差矩阵Γi(t)可以从样本进行估计如下: (30) (31) (32) 式(32)中,向量xi(t-1)=[xi1(t-1),…,xiMi(t-1)]T(其中{i1,…,iMi}∈Ni)收集估计值,ui(t)=[ui1(t),…,uiMi(t)]T收集相邻测量值。 (33) 式(32)的解为: (34) (35) 图1所示为本文提出的估计器实现框图。 算法1 传感器网络中节点i的估计算法伪代码 1.t=0 5.计算ρi 7.xi(0)=ui(0) 8.while|ψi(t)-ψi(t-1)|≥10-10do 9.Mi=|Ni| 10.t=t+1 11.收集估计值xi(t-1)=[xi1(t-1),…,xiMi(t-1)]T,且{i1,…,iMi}∈Ni 12.收集测量值ui(t)=[xi1(t),…,xiMi(t)]T,且{i1,…,iMi}∈Ni 13.计算ρi 16.xi(t)=κi(t)Txi(t-1)+ηi(t)Tui(t) 25.end while 为了验证本文提出的分布式估计器EP的有效性,我们与下列4种估计器进行比较: 1)E1:K=H=(I-L)/2,其中L是与无向图图G相关联的拉普拉斯矩阵; 2)E2:K=0且H=[ηij],如果节点i和j之间通信,ηij=1/Mi,否则,ηij=0,这将得到测量值的平均值; 3)E3:K=[κij],这里,κii=1/2Mi,如果节点i和j之间通信,κij=1/Mi,否则,κij=0,而H=[ηij]且ηii=1/2Mi,其他ηij=0。这将得到先前的估计值和节点的单个测量值的平均值; 4)E4:K=H且如果节点i和j之间通信,且i=j。这将得到先前的测量值和全部局部测量值的平均值。 图2所示为一组跟踪测试信号d1(t),d2(t),d3(t),d4(t)和d5(t),这组信号有不同的频率,把它们作为基准估计。假设已知这些信号Δ的一个上界,把Δ设置为比每个信号的实际值大10%,并选择平均信噪比为γ=1。 下面来分析G35上的分布式估计器得到的信号跟踪估计仿真结果。图3所示为对于d2(t)全部节点得到的仿真结果。 显然,从图3(a)可见,要跟踪估计的测量值是相当嘈杂的,受噪声影响很大。从图3(b)—3(f)可见,全部估计器E1,…,E4和本文提出的分布式估计器EP都能够跟踪信号,但它们的跟踪估计质量有很大的差别。很明显,E1和E2的质量最差,而本文提出的分布式估计器EP有最好的性能。E1,…,E4之间的相对性能差别很明显,如E2简单地采取测量值求平均,而E4是对测量值和估计值求平均,所以E4是优于E2的,而通过适当地选取帕累托参数,本文所提出的分布式估计器EP得到了最好的跟踪估计性能。 图2 数值仿真中采用的跟踪测试信号Fig.2 Tracking test signal used in numerical simulation 图3 不同估计器对于信号d2(t)在每个节点上的N=35个跟踪实现Fig.3 Implementation of N=35 tracking at each node for each estimator and for the signal d2(t) 为了研究本文提出的分布式估计器EP的估值性能,我们考虑每个节点的估计值的均方误差(Mean Square Error,MSE)。由于每个估计器都有一个初始过渡阶段,仿真中计算出了70步后的均方误差,并将网络的全部节点上的均方误差求平均值,把得到的平均值表示为MSE。定义一个估值性能改进因子μi,即采用本文提出的分布式估计器EP的估值性能MSE(EP)与其他4种估计器E1,…,E4的估值性能MSE(Ei)定义为: (36) 表1所示为G25和G35关于全部跟踪测试信号d1(t),d2(t),d3(t),d4(t)和d5(t)得到的MSE和μi。从表1可见,本文提出的分布式估计器EP在全部情况下的估值性能都优于其他4种估计器。具体来说,EP的估值性能至少提高了15%,最高高达85%;而E1较差的性能,主要是E1对节点的本地估计值和测量值的权值通常比从其邻居接收的估计值和测量值的权值要大,因为网络是同质的,所以性能较差;还可看到,当跟踪测试信号频率较高时,EP的性能改善不算太明显,其原因在于,EP估计器总是试图保持最低的偏差,但是以付出更高的估计误差的方差为代价的。 表1 不同估计器的估值性能MSE和改进因子 续表 d3(t),Δ=0.040估计器类型N=25N=35MSEμiMSEμiE1:基于拉普拉斯矩阵E2:对u求平均E3:对x和ui求平均E4:对x和u求平均EP:本文提出的估计器0.4420.6620.3300.3670.22449.0%65.8%31.5%38.4%0.4570.5720.3910.3150.18659.4%67.6%52.5%41.2%d4(t),Δ=0.033估计器类型N=25N=35MSEμiMSEμiE1:基于拉普拉斯矩阵E2:对u求平均E3:对x和ui求平均E4:对x和u求平均EP:本文提出的估计器0.4440.6630.2400.3700.17061.8%74.3%28.8%53.8%0.4470.5640.2560.3080.15066.4%73.4%41.3%51.2%d5(t),Δ=0.000估计器类型N=25N=35MSEμiMSEμiE1:基于拉普拉斯矩阵E2:对u求平均E3:对x和ui求平均E4:对x和u求平均EP:本文提出的估计器0.4360.6560.1950.3580.11473.9%83.8%41.6%68.2%0.4460.5600.1500.3050.08081.0%85.0%44.0%72.0% 本文提出了一种新的用于跟踪传感器网络中未知噪声时变信号的分布式估计器。该估计器采用帕累托优化问题,对滤波器系数进行局部更新,以使估计误差的方差和偏差最小化;提出的分布式估计器相比于现有的分布式跟踪估计器,能更好地跟踪传感器网络中由噪声所损坏的未知时变信号,并能得到更好的估值结果。



1.2 帕累托参数的选取


1.3 偏差上限分析



2 估计器及分布式估计算法
2.1 估计器结构


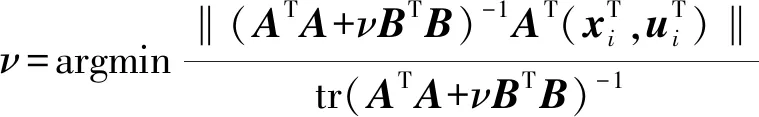
2.2 分布式估计算法

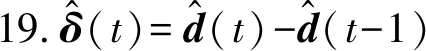

2.3 计算复杂度分析

3 估计器性能仿真结果及分析


4 结论

