解空间定向优化的信号分选算法改进策略

同晓荣

(渭南师范学院计算机学院，陕西 渭南 714099)

0 引言

随着信号分选技术的日益成熟，在国内外引起极大的关注。近年来，相关研究成果大量涌现，主要可以概括为：1)信号分选算法的提出与改进[1-3]；2)信号分选技术在雷达信号处理、声信号处理等不同领域的应用[4-7]。上述研究成果解决了在欠定条件下的不同类型信号的分选问题，取得了较好的效果，主要关注算法的可行性与优越性，但是针对算法在应用过程中的响应速度问题却关注甚少，相关文献只在文中少量提及，并未形成一套系统的方法来解决相关问题。

近年来国内针对信号盲分选问题开展了不少研究，相应的研究成果也逐渐凸显出来。庞利会等人针对单天线接收时频混叠数字信号的盲源分离问题，基于源信号之间载波差异性，构建了单天线接收信号虚拟多通道模型[8]，实现了源信号分离与重构，仿真结果表明了算法的有效性。骆忠强等人提出基于最小误码率准则的盲源分离算法[9]，算法将推导的最小误码率准则结合最大似然原则建立盲源分离代价函数，形成最小误码率约束的代价函数，通过最小化代价函数实现盲源分离，仿真实验也体现出了一定的优越性。赵知劲等人针对短码扩频长码加扰的直扩信号的盲分选问题进行分析，通过特征值分解和酉矩阵去位置模糊实现复合码的盲估计，然后利用m序列的三阶相关函数特性识别短扩频码的类型，最后根据识别结果采用三阶相关法或延迟三阶相关法实现长短伪码的盲估计，仿真实验同样体现出了可行性[10]。

文献[11]中提出了解空间定向优化的快速免疫算法。该算法通过将原始目标函数进行分割，当算法寻找到某一局部极小值后，在原始目标函数的基础上更新搜索区域(减小搜索区域)，则降低了搜索范围内的数据量，能够有效提高收敛速度，通过仿真实验验证了该算法的可行性与优越性。受文献[11]算法改进思想的启发，为减少声音信号分选算法应用过程中的计算量与耗时，对比仿真系统中基于时频单源区域检测的声信号分选算法原理，对信号分选过程中的时频单源区域检测环节实施定向优化，从而简化搜索环节、降低搜索范围，达到提升系统响应的目的。本文针对此问题，提出了解空间定向优化的信号分选算法改进策略。

1 声信号分选算法描述

设声源信号的数量为P，信号接收天线为M元均匀阵列，则在接收天线端，被截获的声信号可以表示为：

x(t)=A·s(t)+n(t)

(1)

式(1)中，x(t)=[x1(t),x2(t),…,xM(t)]T为观测信号矩阵；s(t)=[s1(t),s2(t),…,sP(t)]T为声源信号矩阵；n(t)=[n1(t),n2(t),…，nM(t)]T为噪声矩阵。

A为混合矩阵，用于表征信号在空域中未知的混叠方式，具体表示为：A=[α1,α2…，αP]T，其中αi,i∈(1,p)为列向量，在此对混合矩阵A做出约束：

1)混合矩阵A中，各个列矢量之间不能存在倍数关系，即混合矩阵列满秩。若混合矩阵中αi=kαj，且i,j∈N，i≠j，就会导致源信号中的sj(t)·sj(t)分量无法分离。

2)在不失通用性的前提下，利用混合矩阵的不确定性，将混合矩阵中各列矢量单位化，即‖αi‖=1，i∈1,…，N。

时频分析为解决非平稳信号处理问题提供了一个很好的平台。时频分析是时域分析和频域分析的延伸，它将被处理信号的能量分布在时域和频域上，称为该信号的时频分布图(Time-Frequency Distribution, TFD)。利用短时傅里叶变换(Short Time Fourier Transformation, STFT)将信号转换至时频域进行分析。

对式(1)两边进行短时傅里叶变换，得：

X(t,f)=A·S(t,f)+N(t,f)

(2)

式(2)中，X(t,f)、S(t,f)、N(t,f)分别是观测矩阵、源信号矩阵以及噪声矩阵的短时傅里叶变换的结果。而矩阵A中不包含变量t，因此变换前后不变。考虑噪声后，对于整个时频域上的所有点只对超过噪声能量分布的点进行分析，并称该点为信号单源点，并推导出信号单源点判据。

信号单源点判据：当时频域上存在一点记为(t,f)，在时频域上存在许多这样的点，把这些点组成的区域称为信号单源区域，表征在该点或该区域处信号能量较之噪声能量占主导地位。这些点组成的集合为：

(3)

式(3)中，ξ为判定单源点的阈值。声信号的单源点反映出该点处信号能量在信号时频分布中占主导地位，每一信号单源点处的信号能量是由不同源信号能量加权叠加而成的[9]。

在同一单源点的不同源信号对于该处能量的贡献大小不同，若在该点处的某一源信号能量对于该处总能量的贡献远远超过了其他源信号的贡献时，则称为该点为贡献最大的源信号的时频单源点，同时在信号分选的过程中也认为该单源点处的源信号唯一。

时频单源区域判据：时频域上的信号单源点组成的区域被称为该信号的时频单源区域，在该区域内任意一点(t,f)，都可以得到Si(t,f)≫Sk(t,f)i≠k，即认为在点(t,f)处源信号Si(t,f)的能量贡献最大，认为该点处的能量只由源信号Si(t,f)唯一决定[10-11]。

从上述判据中可以得到以下结论：在混合信号中每一个源信号分量在时频域上都存在着许多离散的信号单源点和单源区域，为下一步的算法实现提供支持，在不依赖信号稀疏性的欠定条件下，解决未知信源个数的通信信号分选的问题。

声信号分选算法的主要步骤可归纳如下。

步骤1 对混合信号进行短时傅里叶变换，将时域信号转移至时频域上：X(t,f)=A·S(t,f)+N(t,f)，利用在时频域上的信号分布X(t,f)来进行信号分选。

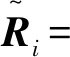
由表1所示，在分选过程中存在较多遍历搜索环节，导致了算法响应速度与计算量急剧增大。因此，为提高算法收敛速度，本文提出基于解空间定向优化(Solution Space Orientation Optimization, SSOO)的改进策略，针对搜索过程进行优化改进。

设时频域上任意一点处的能量幅度由k个源信号能量共同决定的，具体的数学表达式可以表示为：

X(t,f)=(α1S1(t,f),α2S2(t,f),
…,αkSk(t,f))T+Nk(t,f)

(4)

式(4)中，αi为在(t,f)点处的各个源信号混合矩阵的第i行向量；Nk(t,f)为噪声在是时频域上的分布函数。由式(4)可以看出，时频域上任意一点的能量都是由每一源信号和各自权值相乘叠加而成的。当雷达源信号sk(t)的信号主导点集合为Ψ(tki,fki)。在Ψ(tki,fki)中，任意一点(tkε,fkε)的观测信号可表示为：

X(t,f)=αkSk(t,f)+Nk(t,f)

(5)

由于(tkε,fkε)是信号sk(t)主导点集合中的一点，所以对于其他信号包括噪声在该点处的能量幅度很小，推导过程中忽略不计。则在该时频点上的观测信号可进一步写为：

X(t,f)=αkSk(t,f)

(6)

式(6)中,αk为在(tkε,fkε)点处的源信号Sk(t,f)对应混合矩阵的第k行向量，记作：

αk=[αk1,αk2,…,αkM]T

(7)

式(7)中,αk为1×M维向量。得：

(8)

计算天线阵元接收到的观测信号的时频比，得：

(9)

式(9)中,ω表示时频比。

(10)

在计算时频比时发现当观测信号处于信号主导点处的时候，上式可以近似的写成：

(11)

从上式可以看出，每一信号主导点处的时频比为常数，所以只需在时频平面遍历搜索到信号sk(t)全部的信号主导点，按照上述方法，就能够对信号sk(t)所对应的混合矢量进行估计。对应的混合矢量可以写成：

(12)

式(12)中，Lk为信号时频主导点的个数，可以通过主导点判决门限进行判定并求出，在时频主导区域中进行搜索。如果考虑噪声的影响，时频比矩阵就不再为实矩阵，由噪声的时频分量构成复数的虚部，求取矩阵的方法就必须利用聚类特性统计求出。例如当m=1时，对应的时频比矩阵可以表示为：

(13)

(14)

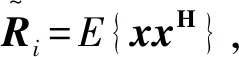
(15)

式(15)中，S为特征值矩阵，并将特征值按照从大到小的顺序依次排列。较大的特征值为混合信号中目标源信号的特征值，而较小的则是噪声特征值。关注其中较大的特征值，其对应的特征向量即为该特征值下的混合估计矢量，即：

(16)

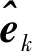
2 SSOO改进策略

文献[11]中，作者在传统免疫算法的基础上增加了药物辅助环节，在该文中指对特定目标函数进行更新，降低搜索范围，从而提高了算法寻优的收敛速度。可以理解为：在目标函数寻优的过程中，当局部极值出现后开启药物辅助环节，更新搜索区域，且新的目标函数区域(搜索区域)小于原始目标函数的搜索区域，即排除了部分不必要的搜索区域，减小了计算量。

在基于时频单源区域检测的声信号分选算法过程中，同样存在搜索环节。本文运用短时傅里叶变换(Short-Time Fourier Transform, STFT)对信号进行时频分析。式(4)为STFT的定义式。

(4)

式(4)中，z(τ)为被分析的源信号；h(τ-t)为窗函数，SZ(t,f)为信号z(τ)的时频分布。信号z(τ)的谱定义为：

(5)

从STFT的定义式中可以看出，对信号进行STFT处理不会产生交叉项，相比于另常用的时频分析方法——维格纳威利分布(Wigner-Ville Distribution, WVD)。

(6)

STFT得到的时频分布分辨力低于WVD，但是WVD存在交叉项的影响，所以本文结合两者优点，定义伪维格纳威利分布(Masked Wigner-Ville Distribution, MWVD)作为源信号时频分布谱图。

(7)

由式(7)可以看出，时频域上信号的分布可以由图1所表示。

如图1所示，空白区域表示时频搜索区域；灰色区域表示信号时频域上的单源区域，即搜索的目标区域；黑色区域表示搜索单元。时频单源区域检测即搜索时频域上的单源区域，即完成搜索。显然，在搜索过程中存在大量的无效区域，即为算法响应速度慢的重要因素。SSOO改进策略将搜索范围不断更新，使得无效区域减少，提高算法响应速度，具体步骤如下。

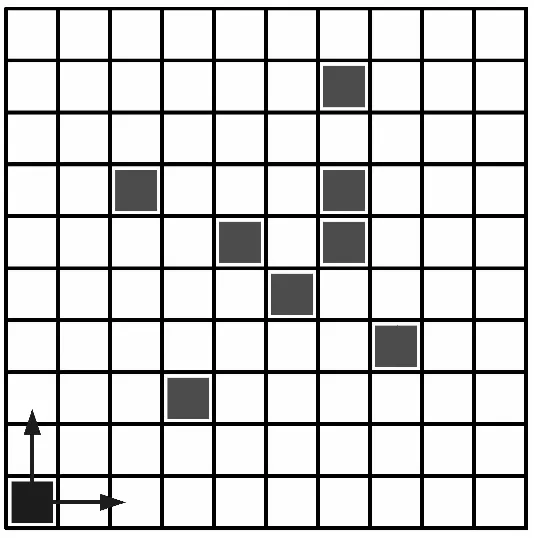
图1 时频域上的搜索环节示意图Fig.1 Search link diagram in time-frequency domain

步骤1 搜索开始后，将源信号时频平面进行“切片”处理，切片并没有“切掉”弱信号，而是将搜索方向唯一确定。则搜索过程即可化简成为在某一方向上(时间T或频率F)的一维搜索。而源信号的时频域“切片”分布可以视为函数求解极大值问题，“切片”上的源信号分布形式如图2所示。

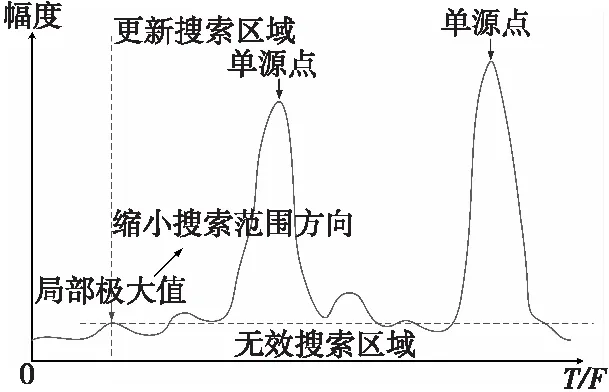
图2 一维搜索探测区域更新示意Fig.2 Updating one-dimensional search detection area

步骤2 一旦按照上述原则对搜索区域划分后，即可对一维曲线进行寻优(本文涉及到的为曲线的极大值，即为单源点)。利用时频单源区域判据对遍历的点进行判别：

(8)

当搜索到目标(时频单源区域)后，随即提高搜索“门槛”，将较小的时频幅值所囊括的区域排除，减小搜索区域。

步骤3 当遍历搜索某一“切片”后，转移至相邻“切片”继续按照优化模式进行搜索，直至整个信号时频区域搜索完毕，将搜索到的信号时频单源点坐标(tss,fss)进行归纳，用于下一步的信号分选。

步骤4 在完成上述三步骤后，根据第1章中的求解解混矩阵的方法进行，完成信号分选任务。

需要说明的是，SSOO优化策略在信号分选过程中，将部分不必要的搜索区域(图1中的白色区域)进行自动剔除，提高搜索效率，极大提升了整个算法的响应速度，使整个信号分选系统的响应时间降低。

3 仿真实验及结果分析

为了验证本文提出的基于解空间定向优化策略的可行性和优越性，利用已搭建完成的SystemVue信号分选平台对该策略进行仿真实验，主要对算法的收敛时间、系统响应时间以及信号分选结果进行监测，并与传统的未优化的信号分选系统进行对比以验证该策略的优越性。利用收敛时间的检测结果来体现信号分选算法的计算量大小。仿真条件如表1所示。

表1 仿真条件与参数

信号分选算法的测试项目的平台中，设定每一发射信号都为线性调频信号，在对每一雷达平台的底层进行设计的时候，模块作为雷达发射信号产生模块，但是不同的是信号分选测试平台未设定各模块之间的位置关系，即无坐标信息，将各模块之间视为在同一位置进行测试。

本次仿真利用的计算机配置如下：Inter Core i5 CPU M450，内存为3 GB；在SystemVue 2017环境下进行仿真实验。

如表2所示，针对本文优化策略的测试共有9组。其中前3组的源信号数目与天线数目为4/4，代表正定情况下的信号分选；中间3组的源信号数目与天线数目为4/5，代表超定情况下的信号分选；最后3组的源信号数目与天线数目为5/4，代表欠定情况下的信号分选。

表2 未优化系统与SSOO优化系统的测试结果比较

从表2可以看出，本文提出的基于解空间定向优化策略在信号分选系统运行时，能够提高计算效率，缩短计算时间。在正定与超定的情况下，该优化策略能够减少50%的系统响应时间，且标准差相较于传统未进行优化系统而言，并未有明显起伏，说明了分选结果的可信度；对于欠定情况下，该优化策略能够减少约30%的系统响应时间，但存在标准差值略微增大的情况。

测试结果能够从计算耗时方面反映出SSOO优化策略针对信号分选系统响应问题相较于传统分选方案的优势。

4 结论

本文提出了解空间定向优化的信号分选算法改进策略，通过在时频单源点处分割目标函数，缩小搜索范围，达到降低计算量的目的，提高算法计算速度。在分析了声信号分选算法改进策略的工作原理、改进思想以及关键步骤后，利用建立的信号分选仿真系统对该策略进行测试，根据上述9组测试结果，能够明显的看出该策略进行优化的系统相较于传统信号分选系统，在不失算法精度的情况下，使系统整体响应速度方面有了大幅度提升。