高质量LMSCT时频分析算法及其在雷达信号目标检测中的应用

郝国成， 张必超， 锅 娟， 张雅冰， 石光耀， 王盼盼， 张 薇

(1. 中国地质大学(武汉) 机械与电子信息学院，武汉 430074； 2. 杜克大学 数学系，美国Durham 27708； 3. 中国地质大学(武汉) 复杂系统先进控制与智能自动化湖北重点实验室， 武汉 430074)

时频分析是处理非平稳信号的重要工具之一，能够将一维时序信号变换到时间频率坐标轴并提供信号频率随时间变化的联合分布关系[1].目前，时频分析方法已经广泛应用于地震信号[2-4]、旋转机械故障信号[5]、金属破裂信号[6]等.海杂波信号也具有非平稳随机的特征，如何提高海面小目标(如浮冰、小船、蛙人以及飞机残骸)的检测能力是一项长期且艰巨的任务[7].传统时频分析方法包括短时Fourier变换(STFT)[8]、小波变换(WT)[9]及Wigner-Ville分布(WVD)[10]等.其中，STFT和WT属于线性时频分析方法，根据海森堡不确定准则，线性时频方法不能同时实现时间和频率的高分辨率.二次型时频分析方法WVD在处理单分量信号时能够得到高分辨率的时频分布，但是在处理多分量信号会出现交叉项干扰，这限制了WVD在现实生活中的应用.

近些年，针对传统时频分析方法的不足，许多优秀的时频分析方法被提出以解决上述的问题.根据选择的窗函数如果和待分析信号的内部特征相近，就会得到聚集度较高的时频表示这种思想.参数化时频分析方法朝着识别信号的内部特征和构造窗函数的方向发展.线调频小波变换(CT)[11]通过引入额外的调频率(CR)参数，在处理线性调制信号时能够得到聚集度较高的时频分布.但是，当CR与信号的瞬时频率差别较大时，通过该方法获得的时频表示存在时频能量模糊现象，不利于信号时频特征的提取[12].后处理时频分析方法通过对时频谱的进一步处理，使得传统时频分析方法的能量谱聚集度得到极大的改善.再赋值方法(RM)[13]通过在时间轴和频率轴方向重排时频点，实现了时频分布的高分辨率.然而，RM是完全依赖时频谱的，导致该方法失去了信号重构能力.文献[14]首先提出同步压缩理论并应用到连续小波变换(CWT).文献[15]将同步压缩理论应用到STFT中，基于STFT的同步压缩变换(SST)极大地改善了STFT时频模糊现象并且保留了信号的重构能力.SST在处理强时变信号时，其时频分布结果会出现分辨率降低的现象.为了克服这一问题，涌现了许多新的时频分析方法，比如2阶SST[16-17]、3阶SST[18-19]、高阶SST[20]等.随着阶数的提高，这些方法的计算量也在不断地增加[21].文献[21]提出一种新的时频分析方法，局部最大值同步变换(LMSST).该算法通过在频率方向检测时频谱的局部最大值，构造一个全新的频率再赋值规则.通过这种再赋值操作，时频分布的分辨率与SST和RM相比进一步得到提高.针对CT存在的问题，本文将LMSST的频率重排规则推广到CT中，提出局部最大值同步压缩线调频小波变换(LMSCT)算法，解决了调频率参数选取对CT时频表示分辨率的影响.同时，仿真实验表明，LMSCT比CT具有更好的抗噪性能.最后，将LMSCT应用到海杂波信号中，为海杂波背景下的小目标检测提供一个可参考的技术手段.

1 算法介绍

1.1 同步压缩理论

一个具有调幅和调频规律的多分量信号f(t)可以表示为

(1)

式中：Ak(t)和φk(t)分别为第k个分量的瞬时幅度和瞬时相位；t为时间变量.

对于一个待分析信号f满足f∈L2(R)，L为勒贝格积分，对应的窗函数g为实函数且满足g∈L2(R)，那么此信号的STFT可以定义为

(2)

式中：ω为信号的瞬时频率；u为时间变量.

SST通过获得STFT的瞬时频率信息，然后进行频率点压缩来提高时频谱的聚集度.要想获得STFT的瞬时频率，首先求取式(2)对时间t的1阶导数，则有：

iωS(t,ω)-Sg′(t,ω)

(3)

STFT的瞬时频率信息ω0(t,ω)可由如下公式求得：

(4)

(5)

式中：δ(·)为狄拉克函数.通过这一后处理操作，可以得到比原STFT聚集度更高的时频分布.

1.2 LMSST算法

作为SST算法的改进方法，LMSST算法定义了一个新的频率再赋值规则，规则如下式所示：

ωm(t,ω)=

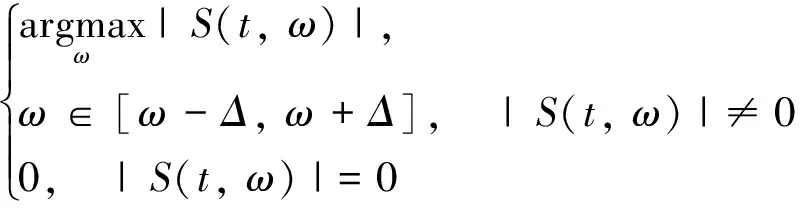
(6)

式中：Δ为离散频率间隔；|S(t,ω)|为STFT的时频谱.假如任意两个分量相隔足够的距离，由于窗函数的Fourier变换在0处达到最大值，式(6)可以简化为

ωm(t,ω)=

(7)

为了获得理想时频分布，所有的模糊时频系数都应该沿频率方向分配到时频轨迹.因此，LMSST可以实现更高的时频能量聚集度，可以表示为

(8)

1.3 LMSCT算法

CT同样是一个非常有效的时频分析方法，通过引入CR参数β，其本身就成为了STFT的推广形式，公式定义为[22]

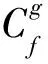
(9)

如果参数β能够很好地匹配待分析信号的调频率，就能够获得能量聚集度较高的时频分布结果.但是对于非线性调频信号而言，此时参数β不能够很好地匹配变化的调频率，因此CT算法在处理这类信号时就会受到限制.

根据LMSST方法的思想，通过对CT的结果进一步处理，在频率方向重新分配时频系数，再赋值规则可以表示为

ωL(t,ω)=

(10)

因此，提出一个新的时频分析方法并命名为局部最大值同步压缩线调频小波变换，算法的定义如以下式所示：

TLMSCT(t,η)=

(11)

传统高阶SST随着阶数的增加，计算量也在相应增加.原始SST需要执行1次STFT步骤，当阶数增加到4时，执行STFT的次数就变为11次.而LMSCT方法只需要执行1次CT，计算量也相对较小.

2 数值实验

为了验证本文提出算法的有效性，需要进行2组仿真信号的实验 ，将本文提出的算法与前文引用的STFT、CT和SST方法进行对比.首先将文献[23]中的仿真信号进行验证，信号1的函数表达式为

f1(t)=sin[2π(10t+5t2/4+t3/9-t4/160)]

(12)

信号1的瞬时频率是时变的并且是单分量的，实验中该信号的抽样频率为100 Hz.根据式(12)，在图1(a)中绘制了信号的真实频率分布，图1(b)展示的是该信号STFT结果，STFT存在严重的能量扩散，不适合分析信号频率随时间变化的关系.在图2中分别使用CT、SST和LMSCT对信号1做进一步处理.

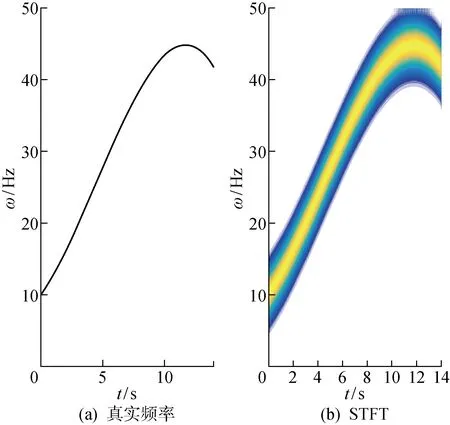
图1 仿真信号1的时频分布Fig.1 Time-frequency distribution of simulation Signal 1

图2(a)的时频分布图由CT得到，且β=4π.同STFT的结果相比，CT在一定程度上提高了该信号时频分布的聚集度.但是从图2(a)中的两处标记可以看出，在瞬时频率较小标记处，CR的值与信号的瞬时频率相近，其时频分布的聚集度相对较好，在瞬时频率较大标记处，CR的值与信号瞬时频率的差别较大，时频能量扩散幅度较大.这两处的对比验证了前文提到的CR值的选取对信号时频分布的影响.图2(b) 和2(c)分别由SST与LMSCT得到.与SST的结果相比，LMSCT的聚集度更高.为了更加直观地比较，分别截取了SST和LMSCT的局部效果图进行展示，截取部分为图2(b)和2(c)中的标记，局部效果如图3所示.图3(a)和3(b)分别为SST与LMSCT的局部展示.通过局部结果的展示可知，LMSCT的聚集度更高.

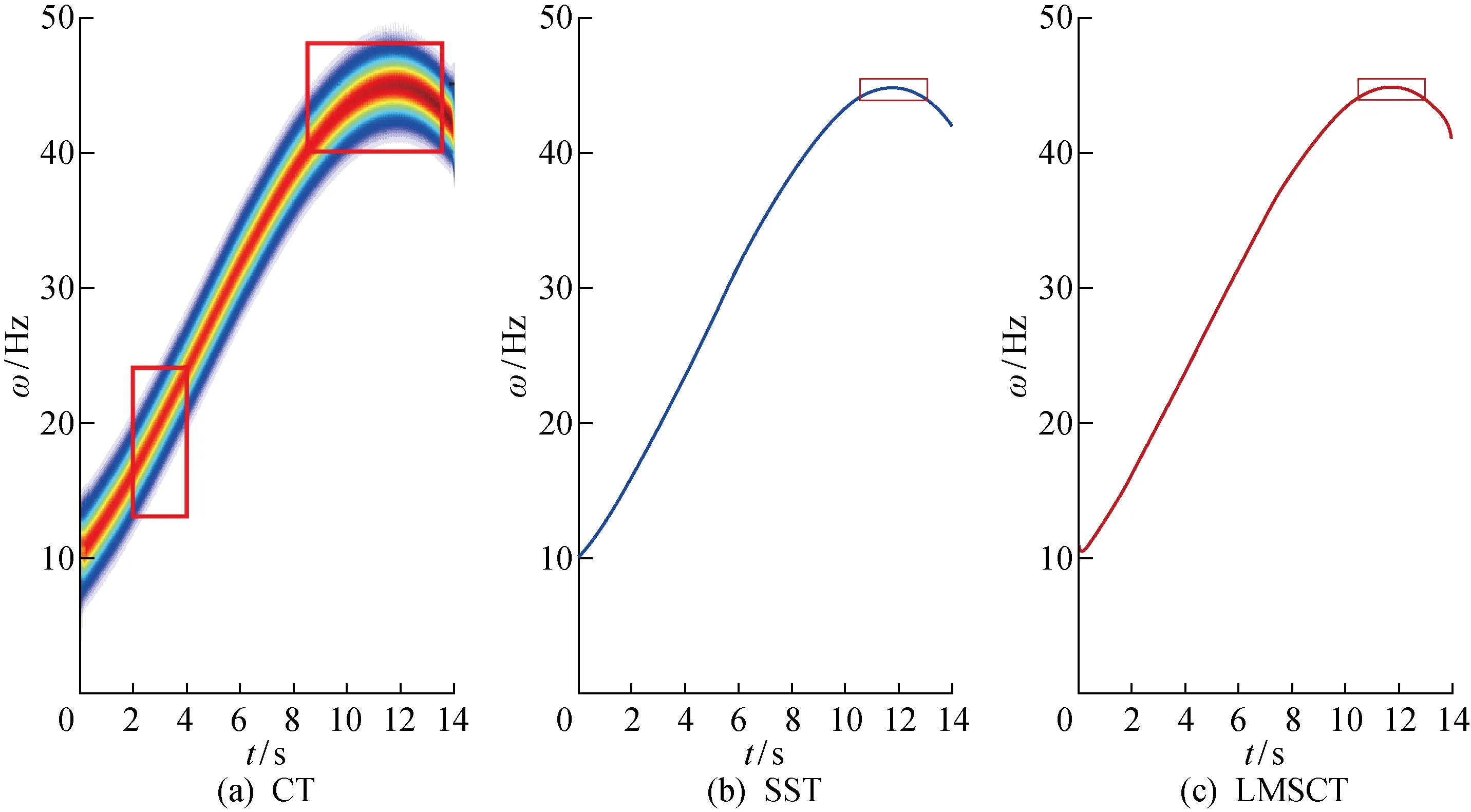
图2 不同算法时频分布Fig.2 Time frequency distributions of different algorithms

图3 时频分布局部效果Fig.3 Local effects of time-frequency distribution

为了系统地比较几种常见的时频分析方法聚集度的高低，在这里引入Rényi熵的概念[24].文献[25]提出将3阶Rényi熵用于提供时频分布的信息度量，文献[24]详细研究了Rényi熵的性质和潜在的应用价值.Rényi熵是评价时频分布能量聚集度的指标之一.Rényi熵越小代表时频聚集度越高，相反Rényi熵越大，代表时频聚集度越低.α阶Rényi熵的计算公式如下式所示：

(13)

式中：T(t,ω)为信号时频分布.一般情况下，α默认为3.其中，信号1在不同算法下的Rényi熵值如表1所示.

表1 不同算法处理信号1得到的Rényi熵

接下来选取一个二分量信号进行仿真验证，信号2的函数表达式为

f2(t)=sin{2π[40t+sin(1.5t)]}+

sin{2π[17t+6sin(1.5t)]}

(14)

仿真实验中，设置信号抽样频率为100 Hz，抽样时间为4 s.信号实际频率分布如图4(a)所示，图4(b)为WVD的时频分布结果.从图4中可以观察到，对于多分量信号，由于交叉项干扰的存在，不能有效提取频率随时间变化的信息，所以WVD不适合处理这类型的信号.将主流的几种时频分析方法与本文提出的方法进行比较，对比结果如图5所示.由图5可知，由LMSCT算法得到的时频分布的能量聚集度比STFT、CT和SST更高.将图5的时频分布转换到三维中，如图6所示，其中：A为幅值；E为能量谱.由图6可以清晰地观察到，STFT和CT的时频分布存在能量扩散的情况；SST与LMSCT能量聚集度较高，然而相较于SST的结果，LMSCT的幅度比较一致，结果更加准确.

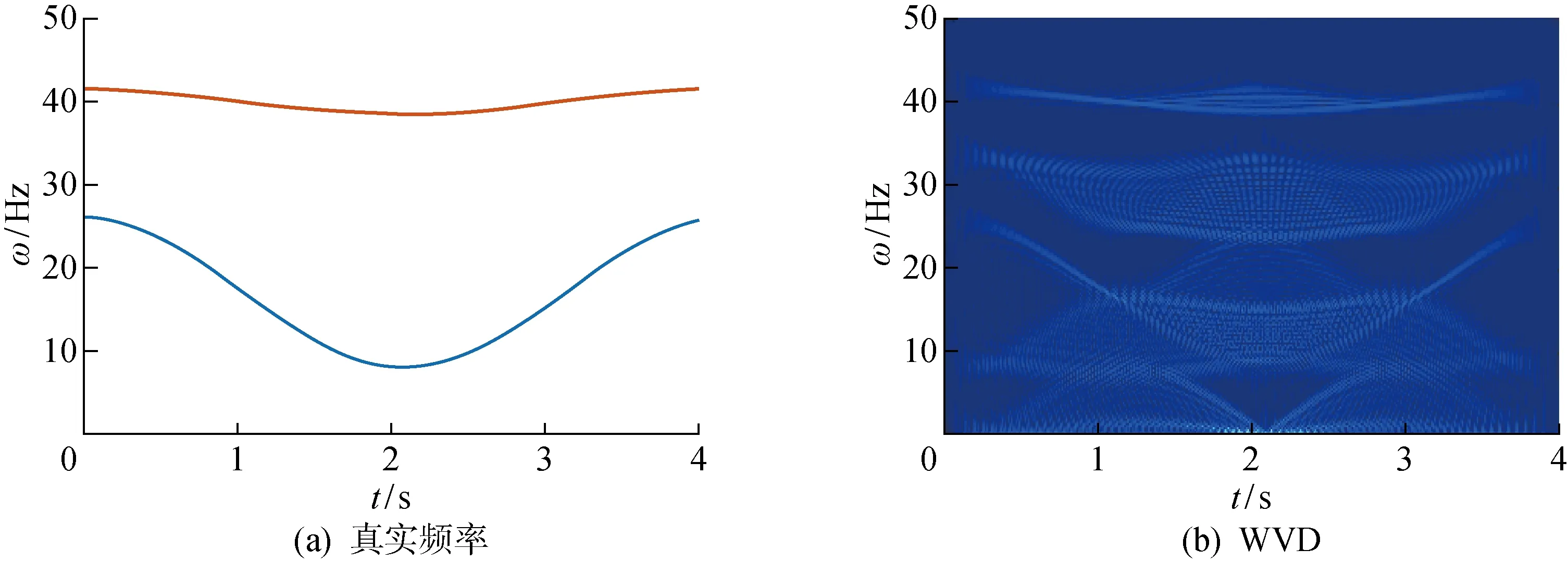
图4 仿真信号2时频结果Fig.4 Time-frequency distribution of simulation Signal 2

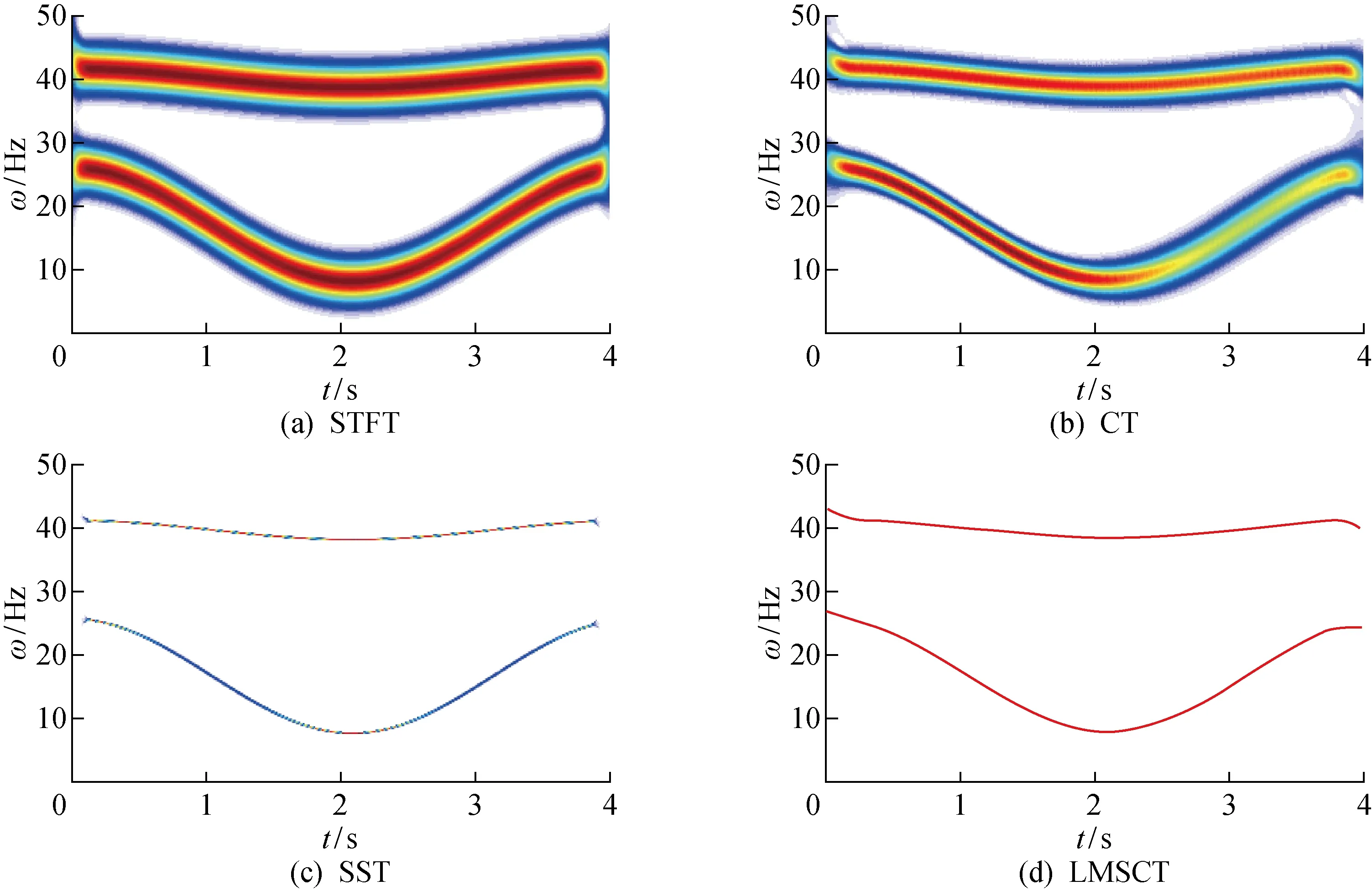
图5 信号2时频分布Fig.5 Time-frequency distribution of Signal 2

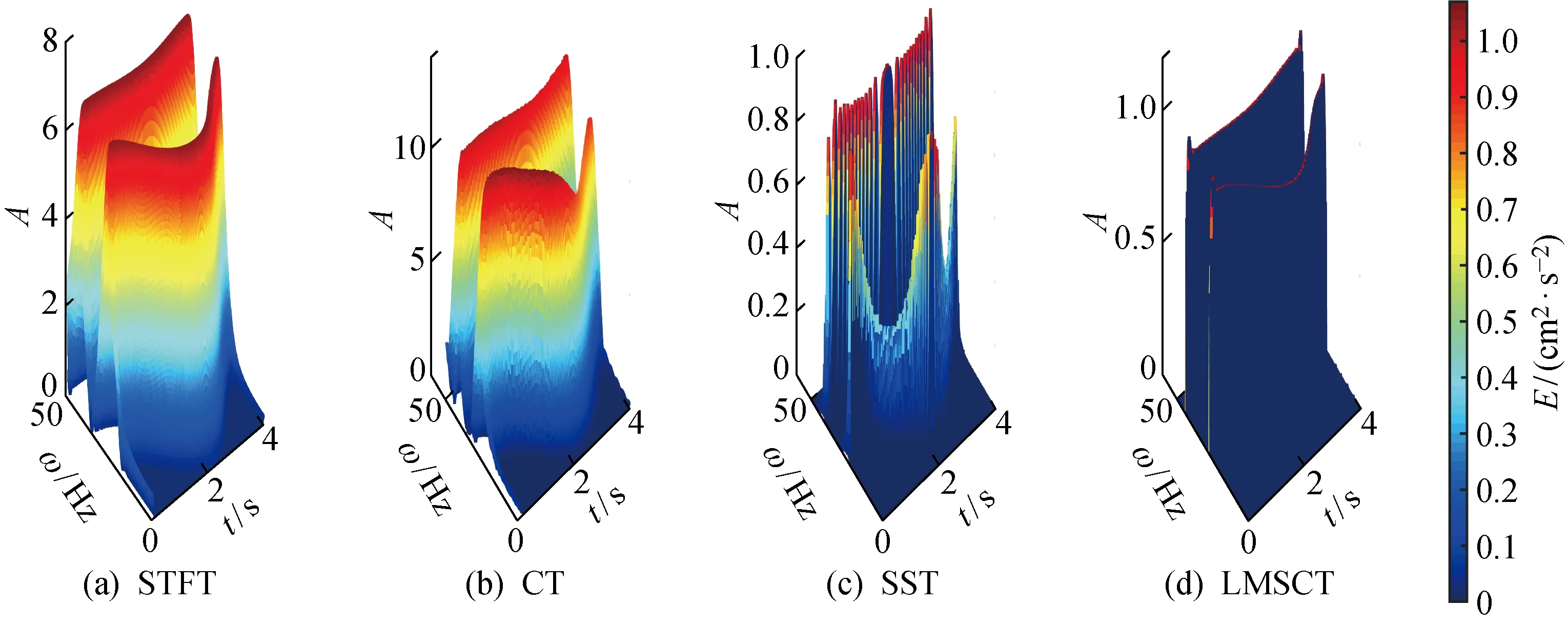
图6 时频分布的三维展示Fig.6 Three-dimensional representation of time-frequency distribution

信号2在不同算法下的Rényi熵值如表2所示.为了更直观地比较，在图7中绘制了Rényi熵值的散点图，其中：R为Rényi熵.

表2 不同算法处理信号2得到的Rényi熵

图7 不同算法的Rényi熵值Fig.7 Rényi entropies of different algorithms

通过表2和图7列出的几种算法Rényi熵值大小的比较，可以确定本文提出的算法具有更高的时频聚集度.通常情况下，现实生活中的真实信号都会含有噪声，将会影响信号时频分布的可读性.接下来对信号2添加高斯白噪声，然后再进行时频分析算法处理，评估不同算法的抗噪声性能.

在信号2中加入信噪比为7 dB的加性高斯白噪声，不同算法的处理结果如图8所示.从图8(a)和8(b)可以看出，受噪声影响，STFT与CT的时频分布不是连续的，严重影响信号时频变化特征的提取.图8(c)和8(d)分别为SST与LMSCT的结果，同STFT、CT结果相比，时频谱能量聚集度都有较大的改善.

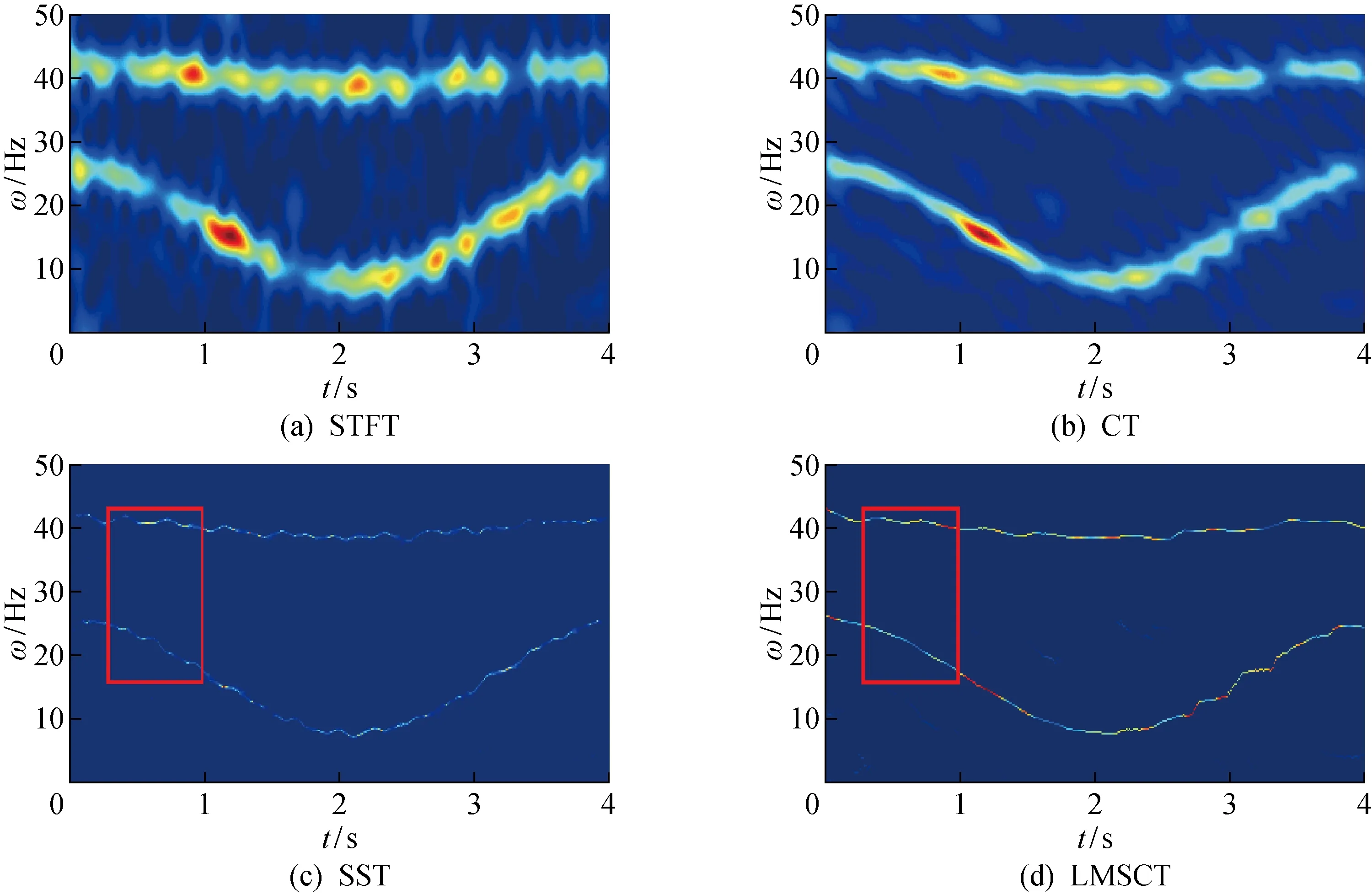
图8 不同算法抗噪效果Fig.8 Anti-noise effects of different algorithms

为了进一步比较SST与LMSCT的抗噪性能，分别截取SST和LMSCT的部分时频表示进行对比，截取部分为图8(c)和8(d)标记部分，局部结果如图9所示.图9(a)和9(b)分别为SST与LMSCT的局部效果.通过对比可以看出，在相同的频率点范围，LMSCT的频率变化曲线比SST更加平滑，而且没有出现能量消失的情况，受噪声影响较小.综上所述，LMSCT算法的时频聚集度更高，且抗噪性能更好.

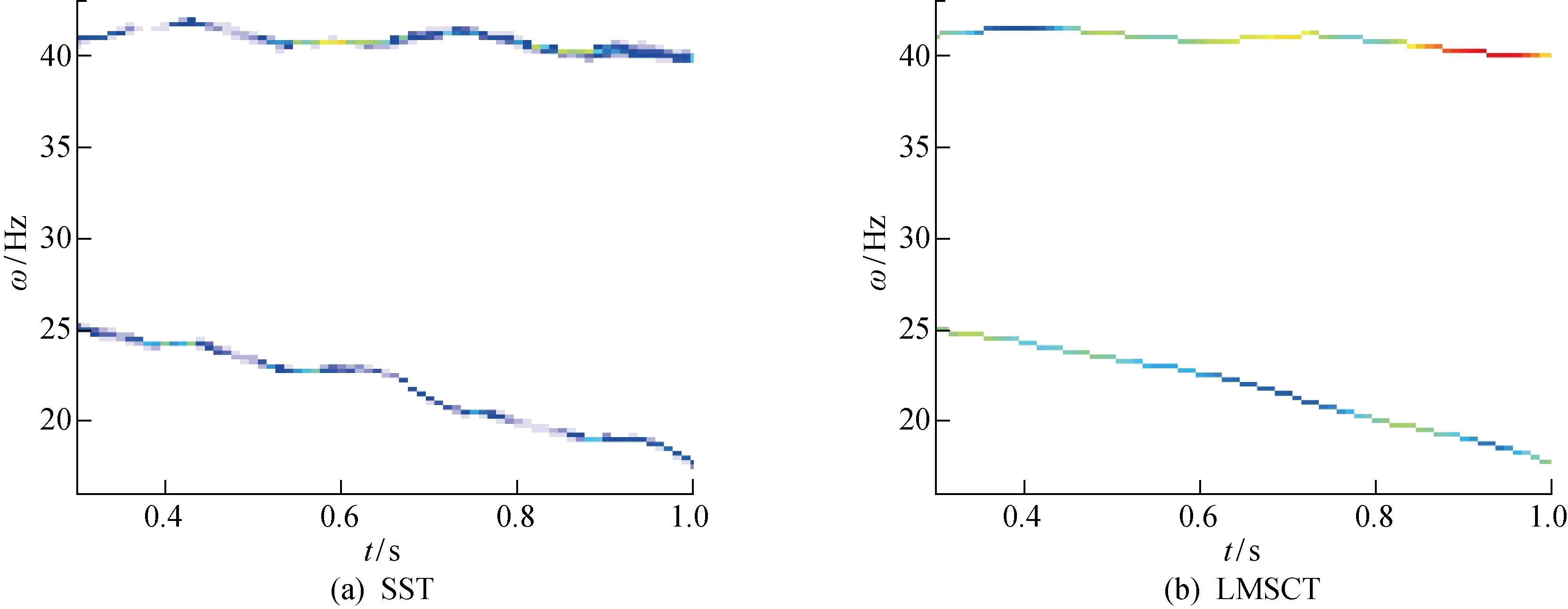
图9 抗噪性能局部图Fig.9 Local diagram of anti-noise performance

3 IPIX雷达数据分析

IPIX雷达由加拿大McMaster大学Adaptive Systems实验室设计，Haykin教授带领其团队分别于1993年和1998年利用IPIX采集并公开了大量高分辨海杂波数据，该数据已经成为测试雷达检测算法的重要基准数据，在海杂波特性研究方面也做出了重要的贡献[26].IPIX雷达是一个全相参的X波段雷达，具有I通道和Q通道两路收发信号.

实验中，雷达架设在加拿大东海岸一个高出海平面25 ～ 30 m的固定位置，雷达朝大西洋海面照射，待检测目标是被铝丝包裹直径1 m的漂浮圆球.雷达工作频率为9.3 GHz，波束宽度为0.9°，距离分辨率为30 m.雷达工作在驻留模式，连续接收来自某一确定方向的海面回波，脉冲重复频率为 1 kHz，驻留时间约为131 s，每组数据包含14个距离单元的回波信号.由于雷达以低掠射角照射目标，目标物体随海面起伏和摆动导致目标能量扩散，并且在进行数据采集时采取了距离过采样，所以目标所在单元周围的临近单元会受到目标能量的影响，记为受影响单元.每个数据文件都由纯海杂波、目标所在单元回波和受影响目标单元回波组成.

测量该数据时的雷达环境参数及数据组成如表3所示.回波信号幅度随距离和时间的变化关系如图10所示，其中：U为距离单元.每个距离单元由 131 072 个时域数据点组成，目标位于第8个单元，距离为2.66 km，由于目标的起伏和漂移，7、9、10这3个单元成为受影响单元.为了进一步分析，本文选取水平发射水平接收(HH)极化下的I通道数据进行处理与分析.

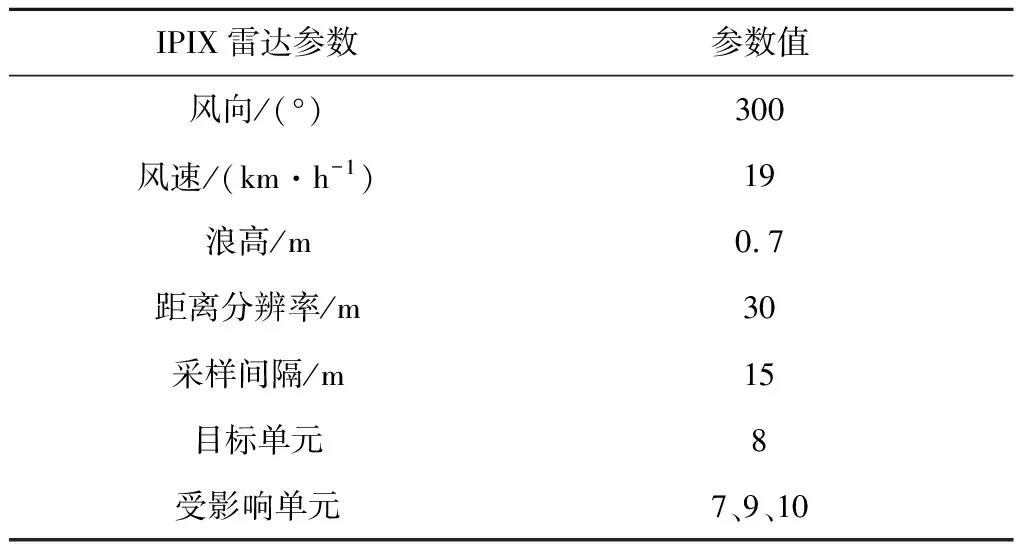
表3 IPIX雷达54#文件环境参数及数据组成

图10 海杂波时间-距离-能量图Fig.10 Didgram of sea clutter time-distance-energy

单元1不是单元8的邻近单元，在数据采集过程中不会受到目标起伏和漂移的影响.首先处理该单元的数据，分析纯净海杂波信号的时频分布结果.单元1纯净海杂波使用3种算法的处理结果如图11所示，其中：Sp为抽样点.从图11(a)和11(b)中可以看出，时频分布结果包含了大量的背景噪声，并且从图11(c)的标记部分展示的结果可知，LMSCT算法较好地抑制了噪声的影响，可以为后续的含噪声信号的处理提供参考依据.接下来将对目标单元及其邻近单元的数据进行处理，对目标单元和其他单元数据的时频分布结果进行分析，提取有效的时变特征信息.

图11 纯净海杂波(单元1)Fig.11 Pure sea clutter (Unit 1)

图12、13、15和16为单元8的邻近单元处理结果，分别为单元6、单元7、单元9和单元10.图14为含有目标的单元8处理结果.由图14可知，对含目标的单元8进行处理后，与单元1的处理结果相比，可以观察到在0频附近出现清晰的频率曲线，并且通过对比图14(a)～14(c)的时频结果发现，LMSCT的频率曲线更加精细，更有利于时频变化特征的提取.从图13、15和16的处理结果中可以看出，由于距离目标单元较近，所以也会出现相似的频率曲线.由图12可知，同样距离目标单元较近的单元6却没有受到影响.这个现象说明，此影响并不是均匀向两边扩散.若不能提前确定单元8是含目标的数据，很难从单元7、8、9、10中确定出目标单元.为了能够进一步确定目标所在单元的位置，采用前文提到的Rényi熵.熵代表信号的无序性，也就是信息量越大，不确定性越小，对应熵值越小.时频分布Rényi熵越小的单元，其含有的信息量越大，即出现目标的可能性越大.单元1、6、7、8、9和10分别使用LMSCT算法得到的时频分布后，计算取得的Rényi熵值如图17所示.从每个单元Rényi熵的散点图可以得出，在单元8的Rényi熵值最小，此单元含有的信息量最大，因此可以判定单元8就是含目标的单元.

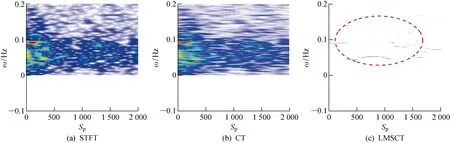
图12 纯净海杂波(单元6)Fig.12 Pure sea clutter (Unit 6)

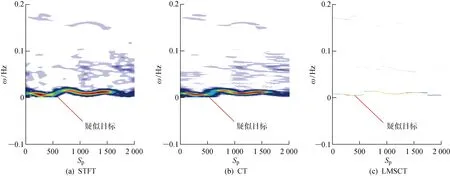
图13 受影响海杂波(单元7)Fig.13 Affected sea clutter (Unit 7)

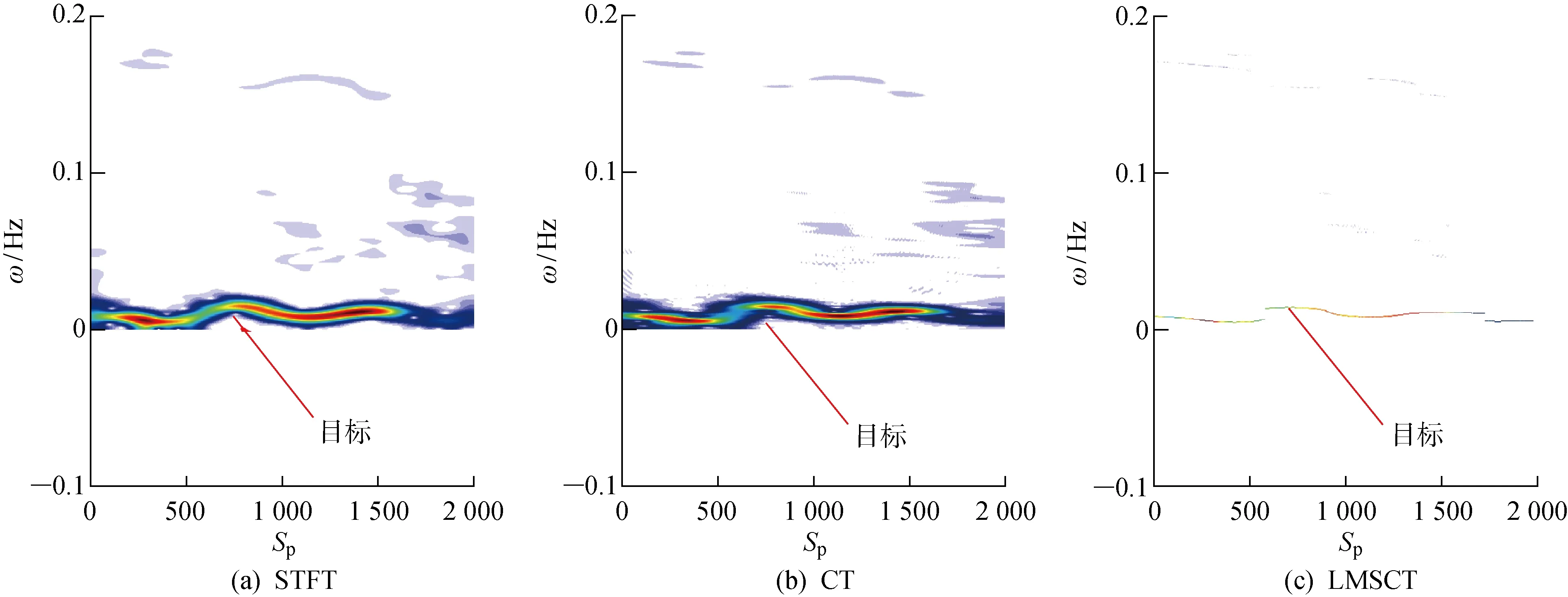
图14 含目标海杂波(单元8)Fig.14 Target sea clutter (Unit 8)

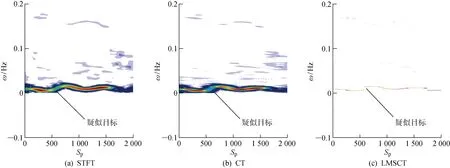
图15 受影响海杂波(单元9)Fig.15 Affected sea clutter (Unit 9)

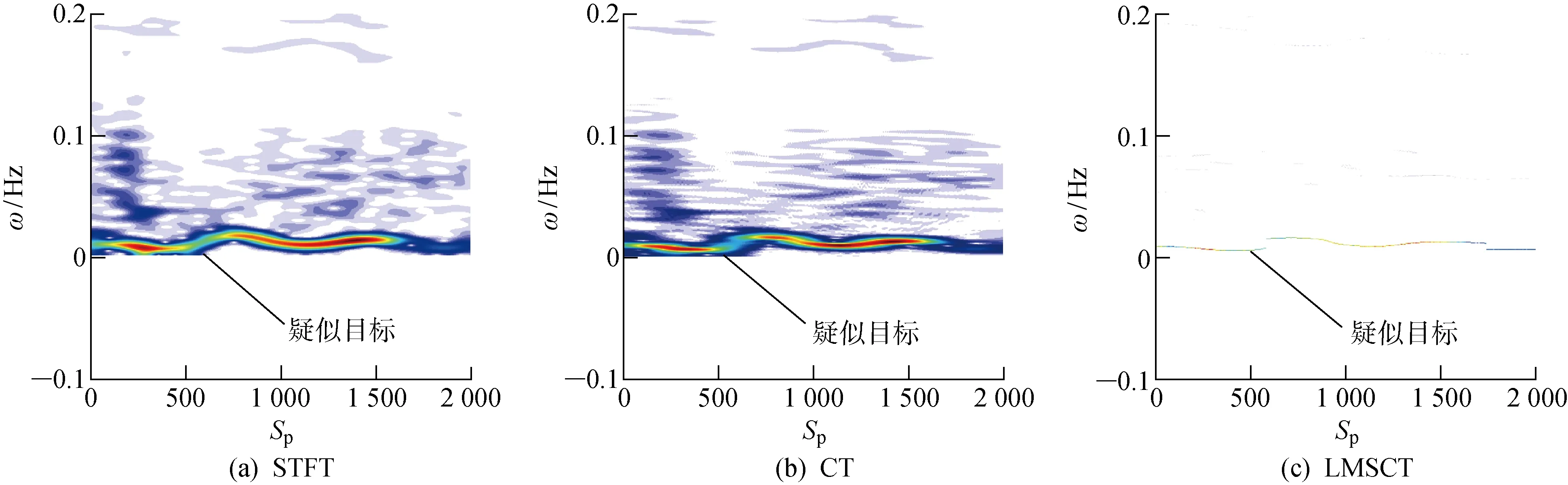
图16 受影响海杂波(单元10)Fig.16 Affected sea clutter (Unit 10)

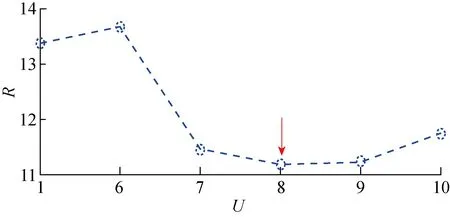
图17 由LMSCT得到的Rényi熵Fig.17 Rényi entropies obtained by LMSCT

4 结语

为提高信号时频分布的聚集度及抑制噪声干扰的性能，本文提出一种新的高质量的时频分析算法，即LMSCT.该算法主要思想是将LMSST与CT算法结合，首先对待分析信号进行CT处理，采用局部最大值同步压缩规则对CT结果进行频率点的重新分配，进而可得到目标信号较为精确的时频分布图.数值实验结果表明，LMSCT与其他时频分析方法相比，该算法时频分布的能量聚集度更高且抗噪声性能更好.实际IPIX雷达信号分析应用中，与目前主流的时频分析算法相比，LMSCT有较小的Rényi熵与瞬时频率聚集度更高的优点以及大幅抑制噪声干扰，通过比较目标信号的Rényi熵，可以有效地确定目标所在的距离单元.