基于变分模态分解的进动目标微多普勒特征提取方法
鲁逸杰,宫志华,张 群,王剑钦,李开明
(1.空军工程大学信息与导航学院,陕西 西安 710077;2.中国人民解放军63850部队,吉林 白城 137001;3.中国人民解放军95333部队,湖南 长沙 410114)
0 引言
弹道目标在飞行时,为了保持姿态稳定,需绕自身对称轴作自旋运动,同时由于弹箭分离以及诱饵释放时形成的横向作用力,目标还将绕空间某定向轴进行进动。美国海军研究实验室(United States Naval Research Laboratory, NRL)的Victor C. Chen最早将进动定义为微动的一种[1]。目标的微动会对雷达回波进行频率、相位等调制,产生相应的微多普勒效应。微多普勒效应反映了目标微动特点,是目标区分的有效独特效应。近年来,基于微多普勒特性进行弹道目标分类识别已成为一个重要研究方向,从雷达回波中准确提取目标微多普勒频率及其微动特征成为目标分类识别的关键。
目前,已有文献对等效散射中心模型下的微多普勒特性进行了研究。文献[2]基于双视角下的距离像序列推导出目标参数的解析解。文献[3]利用多散射中心径向距离历程的关联结果获得了目标的三维运动和三维成像结果,基于三维运动的欧氏重构采用序列二次规划优化和非线性最小二乘循环迭代的方法估计目标的进动参数。文献[4]基于中段目标的电磁散射特性,建立了此类目标在不同姿态下的ISAR成像结果与目标二维几何特征的映射关系,提出一种基于ISAR像的中段目标二维几何特征反演方法。文献[5]通过分析散射点一维距离像随时间变化的规律,提出了一种基于时间-距离像的弹道目标进动特征提取方法。文献[6]提出了一种基于快速傅里叶变换和自适应滤波并结合 Hilbert变换来估计雷达多普勒信号频率的方法。文献[7]基于时频分布,对低信噪比下雷达回波信号瞬时频率进行了估计。
需要指出的是,宽带信号在获得目标微动特征方面的研究较多,而窄带雷达回波多普勒谱中包含的散射点频率变化同样可以反映目标的微动特征。在低信噪比条件下,微动特征的有效提取估计目前仍是一个有待解决的问题。本文针对此问题,提出了基于变分模态分解的进动目标微多普勒特征提取方法。
1 变分模态分解
变分模态分解(VMD)算法是2014年由Dragonmiretskiy等人提出的一种自适应的信号处理方法[2]。该方法在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率和中心带宽,从而能够自适应地实现信号的频域分割以及各分量的有效分离,VMD的分解过程主要分为以下三步:
步骤一 构建目标函数。它分为三步进行:1)对每个模态通过希尔伯特变换计算其解析信号来获得单边谱;2)将各个模态的解析信号与各自指数校准的中心频率混频,将频谱搬移至基带;3)计算解调信号的范数,并估计各模态信号的带宽,构建出目标函数如下:
(1)
式(1)中,{uk}:={u1,…,uk}为所有模态集合,{wk}:={w1,…,wk} 为各模态对应的中心频率。δ(t)为冲激函数,∂t表示对t求偏导数。
步骤二 引出二次惩罚因子α及拉格朗日乘子λ(t),把约束性的变分问题转化成非约束性的变分问题,其中的二次惩罚因子在高斯噪声存在情况下可保证信号重构精度,拉格朗日乘子则使得约束条件保持严格性,扩展拉格朗日的表达式如下:
(2)
步骤三 利用交替方向乘子法来解决上述变分问题,求解上式的迭代过程如下:
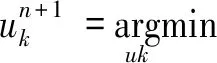
(3)
再将上式变换至频域,得:
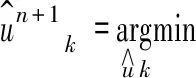
(4)
该二次优化问题的解为:
(5)
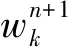
(6)
将上式同样的转化至频域可得:
(7)
该二次优化问题的解为:
(8)
(9)
(10)
(11)
3) 根据式(19)更新λ;
(12)
4) 重复2)和步骤3),直至满足迭代中止条件:
(13)
式(13)中,ε为判别精度,ε>0。
5) 输出结果,得到K个模态。
通过以上算法,可以获得K个模态与其对应的时域波形,即可得到不同频率的信号,由VMD分解得到的信号分量IMF(Intrinsic Mode Function)一般都具有明确的物理意义。在理想的条件下,我们可以通过对时频图形上分离出的微多普勒(micro-Dopple, m-D)曲线进行VMD分解并从中得到一些微动特征参数。
2 基于VMD的进动目标微多普勒频率提取方法
进动锥体目标的等效散射中心主要包括锥顶散射点和锥底散射点,如图1。
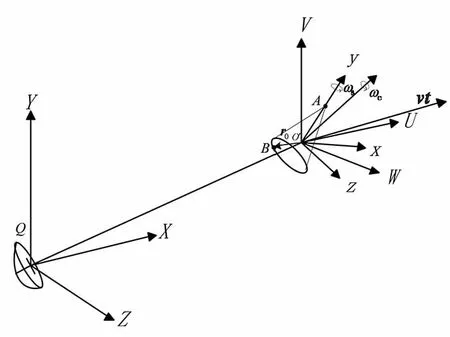
图1 雷达接收机与低空目标的几何关系示意图Fig.1 The geometry of radar and target
假设目标以角速度ωs绕自身对称轴自旋的同时,以角速ωc绕空间某定向轴作锥旋运动。以雷达位置O为坐标原点构建雷达坐标系(X,Y,Z),以目标质心O′为坐标原点构建与雷达坐标系平行,且只随目标的平动而运动的参考坐标系(U,V,W),以目标质心O′为原点构建随目标的运动而运动的目标本地坐标系(x,y,z),目标平动速度为v。由于散射中心A位于锥顶,其自旋线速度为0,因此锥体的进动导致A所对应的微多普勒频率随时间呈现正弦变化[9]。散射中心B除绕进动轴进动外还绕自旋轴进行自旋,所表现的运动为自旋和锥旋的合成运动。
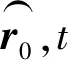
从内容与写作技法言,全词咏茶,而不着一个茶字,却连用若干典故,老练精熟,此笔法在黄庭坚诗中十分常见,将此笔法移之入词,属顺理成章之事。
(14)
式(14)中,t为时间,σ为散射系数,fc为载频,c为光速。对Φ(t)关于时间t求导,得到对应的多普勒频率:
(15)
(16)
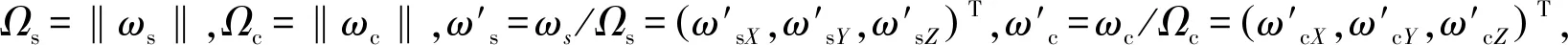
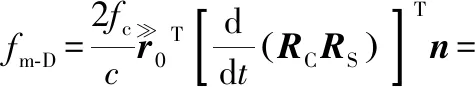
(17)
式(17)中,
(18)
由式(17)可以看出,进动产生的微多普勒频率变化规律表现为多正弦分量叠加,其主要频率分量为自旋频率Ωs,锥旋频率Ωc,及其代数和差|Ωs+Ωc|,|Ωs-Ωc|。
随后,根据上述进动目标散射中心的回波模型,采用时频分析的方法对回波进行处理。Gabor 变换是一个时间-频率分析方法,它采用高斯时间窗口在时域的滑动截取该时段的频谱信息,简单说就是窗口可移动,但是形状不改变。Gabor 变换是高斯窗口短时Fourier 变换,Gabor 变换可以达到时-频局部化的目的,它能够在整体上提供信号的全局频谱信息又能提供局部时刻的频谱变化信息。
通常多散射中心目标的时频曲线会出线交叉,本文首先需要将散射中心A,B的微动曲线的分离开来,再对散射中心B的微动曲线进行分解。文献[10]介绍了一种骨架提取和曲线分离算法,通过对曲线进行行高斯平滑滤波、模值二值化等处理来实现。本文采用此算法对时频图像上的微动曲线进行曲线分离和骨架提取,得到了两个散射中心微动曲线。
高斯平滑滤波具体处理过程是:构建以(x,y)为期望,σ为标准差的二维高斯函数:
(19)
对二维高斯函数进行离散化,得到该二维高斯函数离散射后的函数值。随后将各个位置的坐标带入到离散射化后高斯函数中,得到高斯平滑模板的系数值。设窗口模板的大小为:(2k+1)×(2k+1),模板中各个元素值的计算公式如下:
(20)
式(20)中,i,j分别为时频平面坐标值,经过对时频平面数据的二维卷积,实现高斯平滑滤波。
时频平面数据的二值化是对时频平面复数据取模,对于给定的阈值T,通过调整合适的阈值T,用T将图像的数据分成两部分:大于T的像素群和小于T的像素群。将大于T的像素群的像素值设定为白色(或者黑色),小于T的像素群的像素值设定为黑色(或者白色)。最终得到了两个散射中心微动曲线。
最后,运用VMD算法对两个散射中心的微动曲线进行分解,对于锥底散射点B,在假设平动已补偿的前提下,其m-D曲线为多个正弦分量叠加[9],主要频率成分为自旋频率Ωs,锥旋频率Ωc,及其代数和差|Ωs+Ωc|,|Ωs-Ωc|。对散射点B作VMD分解得到的IMF1为频率成分|Ωs+Ωc|的分量,IMF2分量即为角频率成分为Ωc与Ωs中较大的分量,IMF3分量为角频率Ωc与Ωs中较小的分量,IMF4为成分为角频率|Ωs-Ωc|的分量。与目前已有的用EMD算法来分解m-D曲线的做法相比,VMD算法可以克服EMD算法存在的模态混叠问题,并且具有更良好的抗噪声性能。
3 仿真对比与分析
为了验证VMD方法的有效性和抗噪性,分别进动目标进行无噪和有噪两种情况进行仿真对比与分析。
1)无噪声情况下进动目标微动特征分析能力仿真。
设目标地面半径为0.5 m,高为0.5 m,雷达发射信号载频fc=10 GHz,目标与雷达初始距离为(300 km,100 km,500 km),本地坐标系与参考坐标系的初始Euler角为(π/3 rad,π/4 rad,π/5 rad)。目标平动速度为0,自旋角速度ωs=(19.233 2,-11.107 2,22.214 4)Trad/s,Ωs=10π rad/s,自旋周期Ts=0.2s;锥旋角速度ωc=(8.8813,-10.8773,12.5601)Trad/s,Ωs=6π rad/s。锥旋周期Tc=0.33s,目标上有两个强散射点,即锥顶散射点A(0 m,0 m,0.5 m)和锥底散射点B(0.5 m,0 m,-0.5 m)。脉冲重复率为3 000 Hz,回波信号时长为2 s,图2给出了时频平面上的m-D曲线。对m-D曲线进行高斯平滑滤波和二值化处理的结果如图3所示。对二值化处理的结果进行骨架提取的结果如图4所示。对图4中的两条m-D曲线进行曲线分离,可以准确提取到2条m-D曲线。
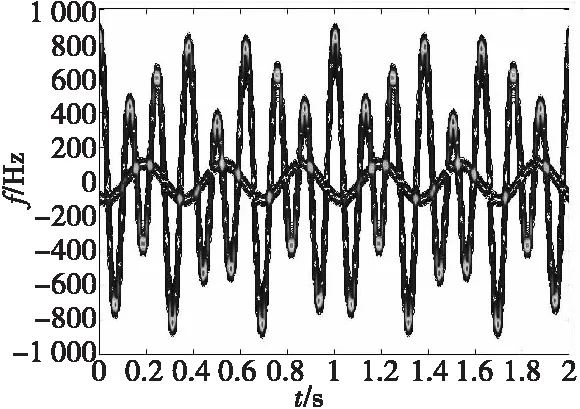
图2 时频分析结果Fig.2 Time frequency analysis result
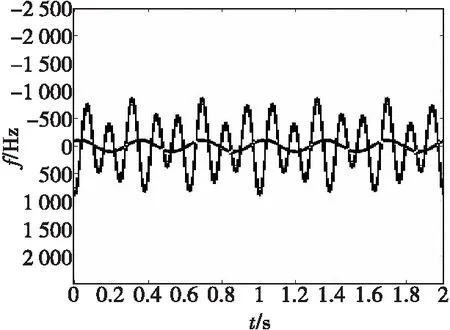
图3 二值化处理结果Fig.3 Binarization processing result

图4 骨架提取结果Fig.4 Skeleton extraction result
分离出的锥底散射点B的m-D曲线,对其分别做VMD分解和EMD分解获得的IMF如图5所示。
从图5可以看出,VMD算法可以清晰地分离出m-D曲线所包含的四种分量。IMF1为8 Hz,IMF2为5 Hz,IMF3为3 Hz,IMF4为2 Hz。而EMD算法的分解结果明显得出现了模态混叠的现象。虽然IMF1仍能得出正确的高频分量,但是由于频率分量比较接近,使得EMD无法准确分辨不同的低频成分。而VMD算法作为一种比较新的非线性信号处理算法,利用变分原理使各个模态不断调整中心频率,比EMD算法具有更好的自适应性,解决了EMD方法的缺陷,分解效果更准确、有效。
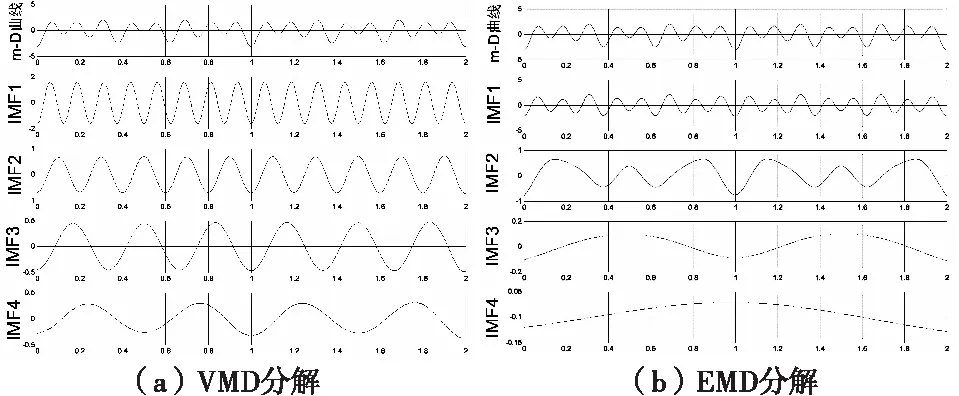
图5 VMD与EMD分解结果Fig.5 VMD and EMD decomposition results
2)有噪声情况下进动目标微动特征分析能力仿真。
在噪声条件下,进一步验证VMD算法和EMD算法的表现。图6给出了在信噪比为-10 dB的情况下。VMD算法和EMD算法的分解结果。可以看出,VMD算法仍然可以提取出除了|Ωs-Ωc|以外的其他分量,而EMD算法不仅仅出现了严重的模态混叠,还出现了无意义的虚假分量。这是因为EMD方法具有二进制滤波特性,对于复杂信号噪声和脉冲的干扰会影响包络线计算,不断传播扩大的误差会产生模态混叠从而导致出现错误的IMF分量,失去了其具体物理意义[11]。而VMD算法本质是一组自适应维纳滤波器,具有较好的噪声鲁棒性。因此在噪声条件下,其分解结果要比EMD算法更准确有效。
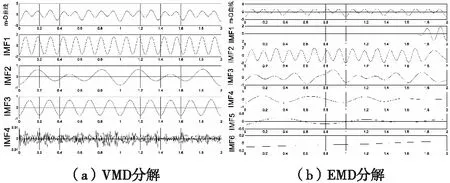
图6 -10 dB噪声下VMD与EMD分解结果Fig.6 VMD and EMD decomposition results under -10 dB noise
4 结论
本文提出了基于VMD的微多普勒频率提取方法。该方法先对Gabor 变换后时频分布结果的进行骨架提取,通过高斯平滑滤波法并结合VMD将回波信号分解成若干独立曲线,并由分解得到的曲线结合其微多普勒曲线特征来估计目标的自旋频率和锥旋频率。仿真结果表明,该方法能够在低信噪比条件下将目标的微动曲线分解成若干独立曲线,并获得其微动频率。

