给水旁路调节下高压加热器的瞬态应力分析

王建华，范佩佩，石峰，种道彤

（1.国网河南省电力公司电力科学研究院，河南省 郑州市450002；2.河南恩湃高科集团有限公司，河南省 郑州市450002；3.动力工程多相流国家重点实验室(西安交通大学)，陕西省 西安市710049）

0 引言

燃煤发电机组面临频繁、深度变负荷的运行需求，开发汽轮机侧储能成为机组提高运行灵活性的一大手段。目前已有的调节策略包括凝结水节流调节、高压加热器调节等[1-3]。其中高压加热器调节主要通过调整回热加热器抽汽量，改变汽轮机内蒸汽流量，从而迅速改变机组功率，该方法具有参数品质高、储热足的特点，成为弥补锅炉储能不足的重要手段[4]。然而高压加热器作为大型高压高温换热设备，在灵活性调节过程中其温度、压力参数波动剧烈，产生的交变应力对疲劳寿命、设备损耗以及安全性运行具有重要影响。因此研究机组灵活性调节方案下的高压加热器瞬态特性，获得温度场和应力场的变化规律，对机组的安全运行和灵活性调节具有重要的意义。

国内外学者对高压加热器的应力分析开展了广泛的研究。在稳态方面，Alam 等[5]对高压加热器换热管某一应力集中最高的管子进行有限元分析，发现最大应力值位于弯头处，且存在安全系数低于1.0 的区域，提出破坏或塑性变形是导致管道泄漏失效的原因；Ananda 等[6]通过实验对高压加热器失效区域进行观察，对奥氏体不锈钢316L 材料作为换热管的应力腐蚀失效进行了评价；高俊等[7]对高压加热器水室隔板存在的穿孔部位进行了局部流场的CFD 仿真，研究发现焊瘤的存在能改变局部流场，流动加速腐蚀并导致加热器穿孔。

在瞬态方面，苑海冬等[8]对1000 MW 超临界机组高压加热器不同运行工况进行了温度动态特性分析，给出了给水温度变化率≤1.83K·min-1下，高加各运行参数的建议调节速率；顾琼彦[9]对某百万等级核电机组的高压加热器受压管板及接管进行了计算分析，通过理论计算及有限元分析方法得到了管板在温度和压力载荷作用下的局部应力，并研究了高加在典型瞬态温度波动工况下的应力强度和疲劳寿命；龚建中[10]对某百万等级高压加热器水室进行研究，将管板简化为等效实心板，进行瞬态过程的热应力分析；Zhao 等[11-12]建立了660 MW 燃煤发电机组瞬态仿真模型，采用高加抽汽节流和给水旁路(feedwater bypass，FWB)两类利用高加抽汽的方法，得到了热力参数和功率的动态响应特性，对抽汽节流方法下高压加热器的瞬态应力进行了对比。

针对高压加热器的研究，前人大多针对其管板、水室等局部应力集中区域进行稳态的应力分析，对于瞬态过程分析很少，尤其是机组频繁变负荷过程中高压加热器的实际动态变化分析。机组1 号高压加热器较其他各级加热器，温度、压力参数更高，且波动更为剧烈，而管板两侧分别是旁路给水和过热蒸汽，存在较大的温差和压力，是整个回热系统最容易发生变形和泄漏的部位[13-14]，因此本文选择某660 MW 超临界燃煤发电机组1 号高压加热器进行研究，建立其三维有限元模型，研究了FWB 调节过程中高压加热器的瞬态温度场、热应力场、机械应力场、耦合应力场的变化，并找到应力集中区域，为高加的安全运行提供数据参考。

1 高压加热器有限元模型

1.1 物理模型

本文对某660 MW 燃煤发电机组1 号高压加热器进行研究，以75%热耗率验收(turbine heat acceptance，THA)工况为基本工况，高压加热器的设计参数如表1所示，各材料物性参数如表2所示[15]。物性参数随温度的变化较小，对瞬态温度场和应力场的影响较小，且不影响分布规律，本文不予考虑。

表1 高压加热器75%THA 工况设计参数Tab.1 Design parameters of 75%THA working condition for high pressure heater

表2 高压加热器材料物性参数Tab.2 Physical properties of materials for high pressure heating equipment

1.2 有限元模型

建立高压加热器管板、换热管、水室和部分壳体在内的三维有限元模型，简化如下：1）换热管数量根据过流断面面积相等的原则[16]进行等效，等效为24 根换热管；2）管板与换热管为胀接方式，建模时不考虑两者接触关系，认为两者互相连接；3）主要考虑管板及附近区域的温度场及应力分布状况，忽略水室人孔密封、分程隔板、防冲板、折流板等部位。

根据高压加热器的结构特点做如下假设：1）假设材料各向同性；2）高加为轴对称结构，建立1/2 对称模型；3）壳侧为蒸汽冷却段和疏水冷却段，不考虑蒸汽相变。采用ANSYS Design Modeler 模块建立高压加热器三维有限元模型，如图1所示，其结构尺寸见表3。

图1 高压加热器有限元模型Fig.1 Finite element model of high pressure heater

表3 高压加热器结构参数Tab.3 Structural parameters of high pressure heater

1.3 网格划分及边界条件

采用ANSYS Mesh 模块对模型进行六面体结构化网格划分，如图2所示。对高加进行网格无关性验证，选择节点1、2 分别对比温度和热应力大小，如图3所示。当网格数量小于158 万时，热应力的变化波动较大，网格数增加到158 万后，温度和热应力基本不随网格数量的增加而发生变化。最终选择网格节点数为158万的模型开展计算。

图2 有限元模型网格划分Fig.2 Meshing of finite element model

图3 有限元模型网格无关性验证Fig.3 Verification of mesh independence of the finite element model

对高压加热器进行温度场计算时热边界条件为：外壁面按自然对流处理，对流换热系数[17]取5 W·m-2·℃-1，对流温度取20℃；对称面及各切剖横截面按绝热处理；水室、壳体内壁面及换热管内外面按第3 类边界条件处理，即给定对流换热系数和工质温度，传热关联式采用Dittus-Boelter 公式。

对高压加热器进行应力场计算时，为消除刚体位移，对结构进行约束，如图4所示。对称面存在对称约束；壳体边缘B处施加x向位移约束；管板横截面C处施加z向远端位移约束。另外，高压加热器应力分析过程中考虑重力的影响，在重心A处施加9.8 m·s-2重力加速度，方向为-z向。

图4 高压加热器约束情况Fig.4 High pressure heater constraints

1.4 模型验证

对高压加热器有限元模型进行验证，参考文献[18]建立600 MW 机组高压加热器水室简化模型，模拟试验压力为10.3 MPa 下的等效应力分布。仿真结果与文献中实验数据对比见图5。2种方法下应力较大部位均出现在测点4 和26，为高加水室封头与管板的连接处；相同压力工况下，实验应力与仿真应力的变化趋势一致，偏差在允许范围内。综上认为模型可靠，有限元方法正确。

图5 不同测点等效应力对比曲线Fig.5 Equivalent stress comparison curves for different measuring points

2 应力分析

2.1 边界条件与载荷

基于GES JTopmeret 模块建立的660 MW 燃煤发电机组动态仿真模型[11,19]，得到不同给水旁路调节工况下1 号高压加热器各出入口的温度、压力动态变化数据。模型将高压加热器蒸汽侧、给水侧和换热板简化为若干节点，各节点大小相同；通过各节点的温度分布表征高压加热器全场的温度分布。

本文研究了3 种给水旁路调节工况：给水旁路程度20%(FWB 20)，给水旁路程度60%(FWB 60)，给水旁路程度100%(FWB 100)，其中旁路程度代表旁路中给水的流量占总给水流量的份额。各热力参数如图6所示。0～100 s 是稳定运行阶段，t=101s 时刻开启旁路阀门，t=301 s 时关闭旁路阀门，恢复给水至初始阶段；3 种FWB 工况对应的阀门执行时间分别为12、36、60 s。蒸汽侧压力先增大，然后逐渐恢复到初始状态，这与加热器的自平衡能力有关；水侧压力在t=101s 时开始波动，存在2 个谷值是因为压力传播过程中遇到阀门阻挡产生震荡，在t=750s 左右压力逐渐恢复到初始值；蒸汽温度增长缓慢且有一定的波动，这是逆流式加热器传热时间延迟所致，且波动范围随着旁路程度的降低而降低；给水温度先快速升高后迅速下降，在小范围内波动至恢复稳定，相比蒸汽温度恢复速度更快。可以看出，蓄热的传播速度比压力波的传播速度慢。

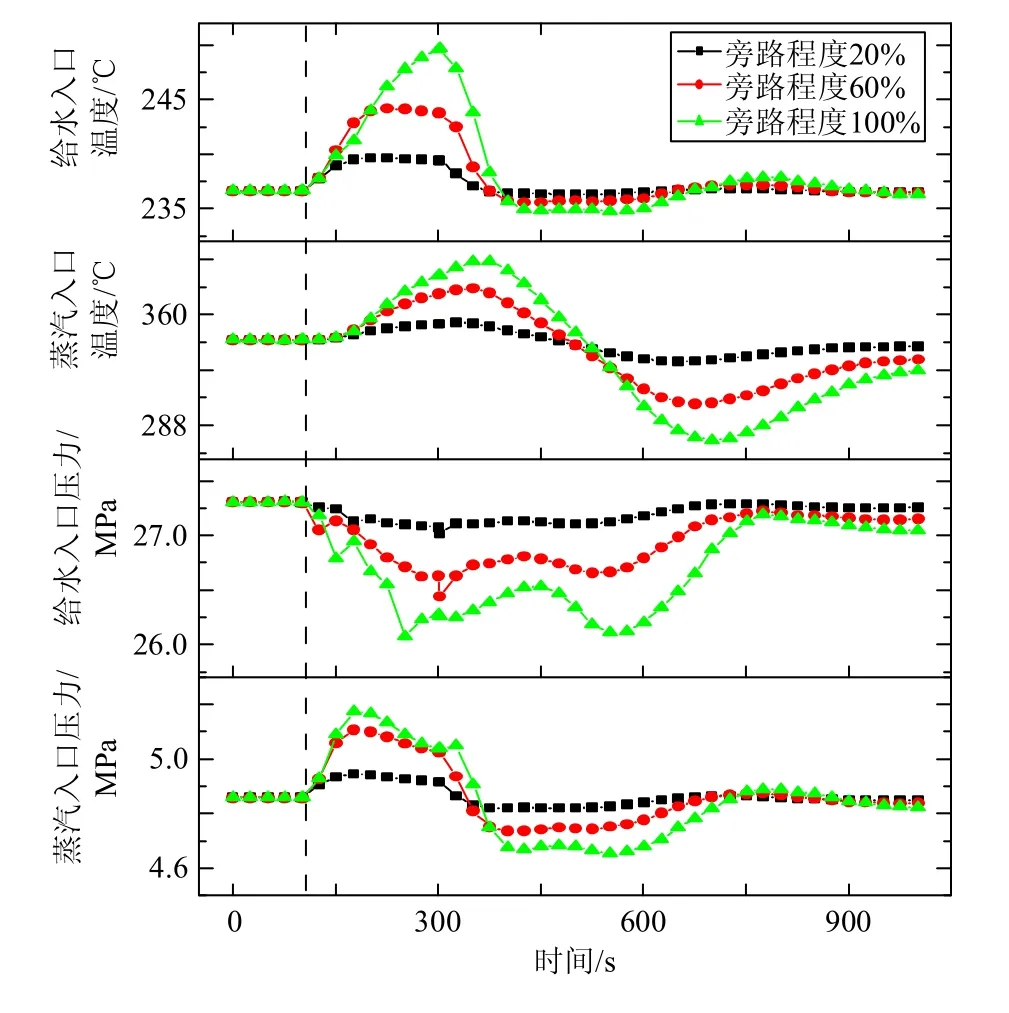
图6 高压加热器在FWB 工况下热力参数动态特性Fig.6 Thermal parameters dynamic characteristics of high pressure heater under FWB condition

利用加热器各区域的一维数据作为ANSYS Workbench 中有限元分析模型的温度载荷和压力载荷，对高压加热器进行不同瞬态工况的计算与分析。

基于Workbench 的有限元分析，可以得到瞬态过程高压加热器的温度场和应力场分布，其中应力场又包括热应力场、机械应力场和耦合应力场。由于FWB100 是给水旁路工况中高压加热器温度、压力波动最剧烈的工况，下文以FWB100过程为例介绍瞬态场的分布。

2.2 温度场分析

高压加热器各时刻的温度场分布如图7所示。整体温度呈先升后降的趋势，但给水出口部位呈先降后升的趋势；t=100 s 时最高温度为343.6℃，位于蒸汽入口区域；t=175 s 时给水出口温度快速下降，是由于FWB 100 时给水经旁路直接送往锅炉，1 号高压加热器水室出口的内壁面受此影响温度明显下降；t=300 s 时给水出口区域温度继续下降，蒸汽入口管温度升高至383.0℃，是由于换热管内给水流量少，蒸汽保有较高的温度，此时高压加热器整体温差最大；之后高加给水开始恢复，在t=375s 时阀门已完成执行恢复到关闭状态，给水完全由水室进入，此时蒸汽侧温度为394.1℃；t=500s，1000 s 下高压加热器温度持续降低，最高温度均出现在蒸汽入口管处。在FWB 100 工况下，高压加热器蒸汽入口管区域始终是温度最高的部位。

2.3 应力场分析

2.3.1 热应力场

高压加热器各时刻的热应力分布如图8所示。热应力整体呈先升后降的规律，t=100s 时最大值出现在管板与壳体连接转角处，是由于该处结构刚度存在突变，造成了局部应力集中；t=300s时最大值为252.8 MPa，出现在蒸汽入口管区域，此时水室出口区域保有较大的热应力；t=375s 热应力最大值同样位于蒸汽入口管，蒸汽侧由于热惯性其应力继续小幅上升，此时水室中给水完全恢复流动，水室进出口区域的内壁面温度上升，减小了内外壁温差，热应力开始下降；在t=500 s和1000 s 时各区域温差减小，温度分布趋于稳定，热应力持续降低，热应力分布与初始时刻分布规律一致。

2.3.2 机械应力场

图8 高压加热器在FWB 100 工况下的热应力场分布Fig.8 Thermal stress fields of high pressure heater under FWB 100 condition

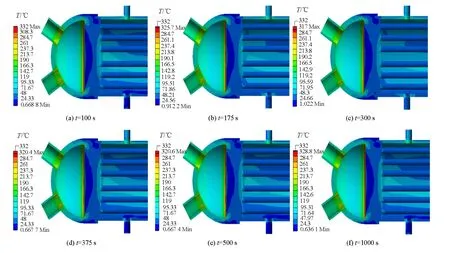
图9 高压加热器在FWB 100 工况下的机械应力场分布Fig.9 Mechanical stress fields of high pressure heater under FWB 100 condition

高压加热器各时刻的机械应力分布如图9所示。各时刻下应力分布规律一致，最大值在317.0～332.0 MPa 范围内波动，均出现在管板与水室弧侧连接区域；水室区域机械应力高于壳侧，蒸汽入口管机械应力高于疏水出口管；给水旁路过程中，水室入口和出口中始终有部分给水滞留，压力变化幅度不大，因此该过程对高压加热器的机械应力影响很小。

2.3.3 耦合应力场

图10 高压加热器在FWB 100 工况下的机械-热耦合应力场分布Fig.10 Mechanical-thermal coupled stress fields of high pressure heater under FWB 100 condition

高压加热器各时刻的耦合应力分布如图10所示。耦合应力呈先增大后减小趋势，t=100 s 时耦合应力最大值为398.1 MPa，出现在管板与水室弧侧连接区域；t=175 s，300s 时耦合应力最大值分别为495.7、529.1 MPa，最大值均出现在管板上侧与水室弧侧连接区域，此时水室出口较水室入口有较大的耦合应力，是由于该部位的汽水参数波动更大；恢复给水后高压加热器应力逐渐降低，t=375 s 时最大值为412.6 MPa，出现在管板与水室出口弧侧连接处；t=500 s、1000 s 时，最大值分别降为383.8、387.5 MPa，此时机械应力起主要作用，应力分布规律与初始时刻一致。FWB 100 工况下耦合应力最大值始终为管板与水室弧侧连接区域。

2.4 不同瞬态工况应力对比

通过分析发现，在给水旁路调节过程中，蒸汽入口管处有较大的热应力，水室出口处的温度和热应力随时间变化较大，管板处的机械应力和耦合应力始终较高，因此针对高压加热器选择了水室出口(A)，蒸汽入口管(C)，管板上侧(E)、管板下侧(F)4 个关键部位进行局部应力的对比，关键部位分布如图1所示。

2.4.1 关键部位热应力对比

图11 不同给水旁路工况下高压加热器关键部位的热应力变化规律Fig.11 Thermal stress variation in key parts of high pressure heater under different feedwater bypass conditions

关键部位热应力的变化规律如图11所示。A区域热应力先快速升高后降低至恢复平稳，FWB 100 工况下应力变化最剧烈，在t=300 s 时达188.57 MPa；FWB 20、FWB 60 和FWB 100 工况下该区域的热应力波动幅度比为0.132:0.547:1。C区域热应力呈先升后降的趋势，其中FWB 100工况下存在2 个峰值，在t=300 s，400 s 时出现，且第1 个峰值高于第2 个峰值，是因为蒸汽入口温度受调节影响快速变化时，管外壁面温度变化存在滞后性，导致了C 区域内外壁温度存在2 个较大的温差；3 个工况下热应力波动幅度比为0.241:0.557:1。E 区域在FWB 60、FWB 100 工况下热应力存在明显的峰值和谷值，FWB 100 工况下热应力最高达230.11 MPa，FWB 20 工况应力波动很小，说明旁路程度较小时对C 区域热应力影响小；3 个工况下热应力波动幅度比值为0.066:0.431:1。F区域热应力在FWB 20 和FWB 60工况下热应力变化幅度小，其中FWB 60 在500 s之后存在明显的波动，FWB 100 工况的热应力先下降至较小值，300 s 进行恢复抽汽后热应力继续下降至更小值，且该区域的热应力较其他部位波动更大，不易达到稳定；3 个工况下该区域的热应力波动幅度比值为0.175:0.633:1。

综上可知，A 区域热应力恢复较快，F 区域热应力需要更长的时间恢复平衡，C 区域热应力值最高；4 个关键部位的热应力波动幅度均随着给水旁路程度的增大而相应增大。

2.4.2 关键部位机械应力

关键部位机械应力的变化如图12所示。A、E、F 区域机械应力有相同的变化规律，均存在2个明显的谷值，100 s 时机械应力开始下降，250 s左右到达第1 个谷值，在450 s 左右开始第2 次下降，550s 左右到达第2 个谷值，但第1 个谷值的数值更小，说明FWB 调节下旁路阀门突然关闭会引起更大的压力震荡。在FWB20、FWB60 和FWB100 工况下，A、E、F 三个区域的机械应力波动幅度比值分别为：0.175:0.565:1，0.197:0.577:1，0.200:0.582:1。C 区域机械应力先上升后下降至平稳，3 种工况下峰值较接近，应力变化幅度很小，说明FWB 调节过程对蒸汽压力影响很小；该区域在不同给水旁路工况下机械应力波动幅值比为0.278:0.775:1。各区域的机械应力波动幅度均随着给水旁路程度的增大而相应增大，在FWB 100工况下应力变化幅度最大。

2.4.3 关键部位机械-热耦合应力

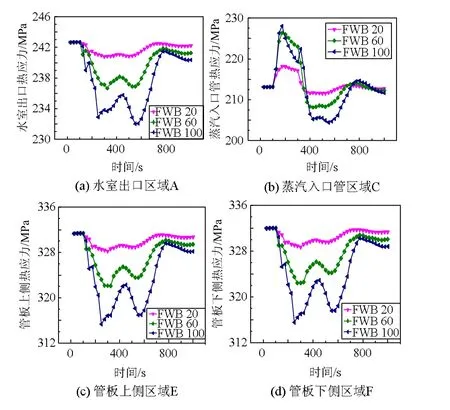
图12 不同给水旁路工况下高压加热器关键部位的机械应力变化Fig.12 Mechanical stress variation in key parts of high pressure heater under different feedwater bypass conditions

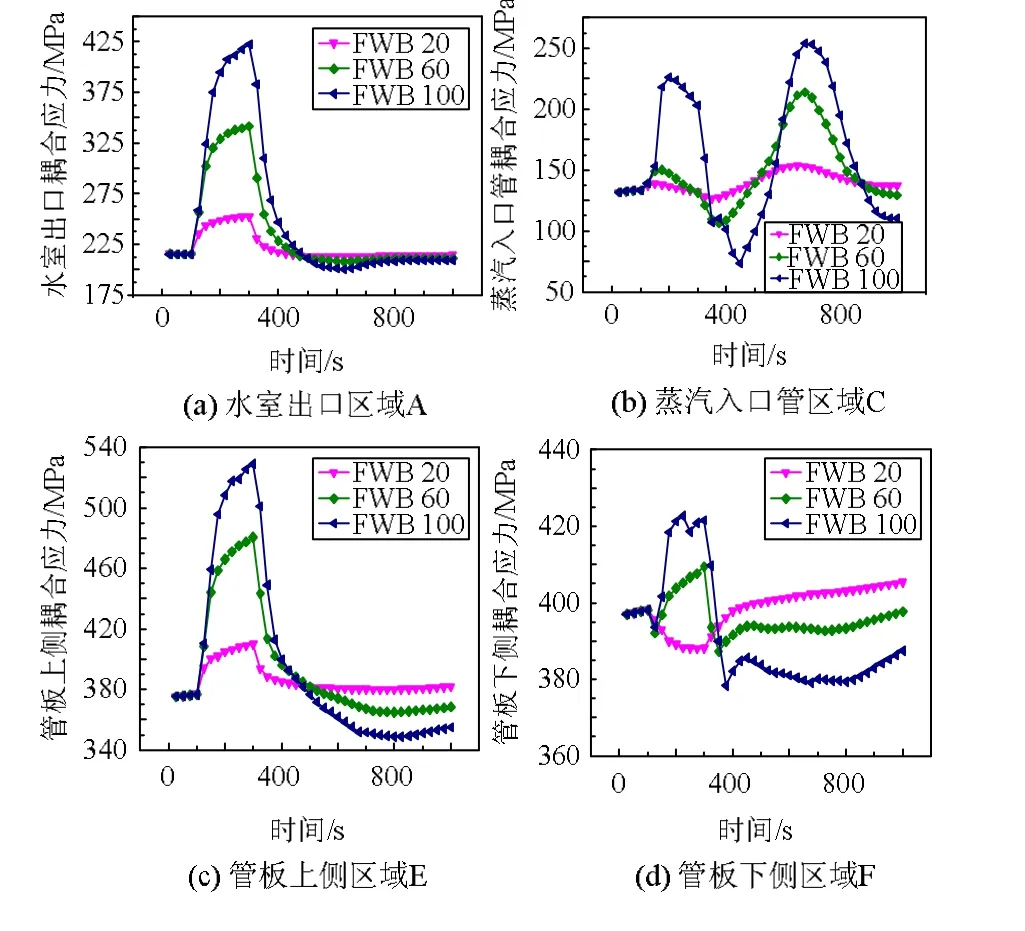
图13 不同给水旁路工况下高压加热器关键部位耦合应力变化规律Fig.13 Coupling stress variation in key parts of high pressure heater under different feedwater bypass conditions

关键部位机械-热耦合应力的变化见图13。A 区域耦合应力在100 s 时快速升高，300 s 之后迅速下降并恢复稳定，与热应力变化规律相似；该部位在3 个工况下的耦合应力波动幅值比为0.179:0.603:1。C 区域耦合应力在400 s 后存在明显的2 次波动，且峰值更高，3 个工况下耦合应力波动幅值比为0.150:0.596:1。E 区域耦合应力在100s 时快速升高至峰值，300s 之后快速降低，在恢复稳定的过程中存在波动，且波动范围随旁路程度的增大而增大；该区域在3 个给水旁路工况下的耦合应力波动幅值比例为0.193:0.641:1。F区域在FWB 20 工况下耦合应力先降后升，在FWB 60 和FWB 100 工况应力在先小幅下降后升高，400s 后逐渐趋于稳定，应力波动幅度小于E区域；F 区域的耦合应力在100 s 左右小幅下降，该时间段机械应力小幅下降，热应力由于延迟保持稳定，两者耦合后下降；3 个工况下该区域的耦合应力波动幅度比值为0.390:0.501:1。

综上可知，E 和F 区域的耦合应力远高于其他部位，其中E 区域为耦合应力分析中最危险的部位，在FWB 100 工况下应力最大，达529.13 MPa；给水旁路程度越大，各部位耦合应力的波动幅度越大。

对比4 个关键部位的热、机械、耦合应力波动幅度发现，各应力的波动幅度均随着给水旁路程度的增大而增大。

3 结论

对某660 MW 燃煤发电机组1 号高压加热器进行了有限元瞬态过程分析，分别研究了给水旁路20%、给水旁路60%、给水旁路100%三个工况下的温度场、热应力场、机械应力场、耦合应力场分布，并对水室出口、蒸汽入口、管板上侧、管板下侧4 个关键部位进行了工况对比，具体结果如下：

1）对比4 个关键部位的热、机械、耦合应力的波动幅度发现，给水旁路程度越大，各种应力的波动幅度都相应增大；各给水旁路工况中，给水旁路100%为最危险工况。

2）各给水旁路工况下，高压加热器整体温度呈先升后降的趋势，给水出口部位温度呈先降后升的趋势；仅考虑热应力时蒸汽入口管为应力集中最大部位，仅考虑机械应力时管板下侧为应力最大部位，但各区域波动幅度始终较小，综合考虑热、机械作用的耦合应力时，管板上侧区域应力集中最高，为高压加热器最危险的部位，需重点关注和检修。