含Ornstein-Uhlenbeck过程的随机SIS模型疾病的灭绝性分析
李海燕,韦煜明,彭华勤
(广西师范大学 数学与统计学院,广西 桂林 541004)
0 引言

(1)

值得注意的是, 大多数学者在研究环境变化对传染病的影响时, 所考虑的白噪声扰动都是线性的, 此外, 模型中的参数也可能满足均值回复过程(i.e.,Ornstein-Uhlenbeck过程).[11-14]假设接触系数β满足均值回复过程, 其形式如下:
dβ(t)=θ(βe-β(t))dt+ξdB(t)
(2)
其中,θ和ξ为正常数,θ为回复速率,ξ为波动强度,βe为接触系数的长期平均水平. 对(3)式积分, 得到

(3)
其中β0:=β(0).易知β(t)的期望为E[β(t)]=βe+(β0-βe)e-θt
(4)
β(t)的方差为
(5)

因此, (3)式可写成如下形式
(6)

(7)
本文在文献[12]的基础上, 考虑总人口变化和因病死亡率, 并且接触系数满足均值回复过程, 得到如下模型:
(8)
其中B(t)为标准布朗运动, 因为当染病者人数较少时, 人们重视程度不高, 没有通过采取措施来控制接触率, 此时感染力是增加的; 当染病者增加时, 人们开始重视, 从而通过采取一些手段来控制接触率, 进而降低了感染力, 此时感染力是递减的. 所以感染力度是一个非单调的函数, 因此, 为了确保有一个非单调的感染力, 我们做出如下假设:
(H1)f(0) >0并且f(I)′ >0,(I>0)

本文主要讨论模型(8)全局解的存在唯一性以及疾病灭绝的条件.
1 全局正解的存在唯一性
本文总假设(Ω,F, {Ft}t≥0,P)是一个完备的概率空间, 其中{Ft}t≥0满足通常条件,

显然Γ是系统(8)的一个正不变集.



τη=inf{t∈[0,τe):S(t) ≤η,S(t) ≤η}

P{τη≤T}≥ε,
显然,V(S(t),I(t))是正定的.根据It公式, 我们有:

(9)
其中

:=M
将其带入(9)式有:
(10)
对(10)式从0→τη∧T积分, 有
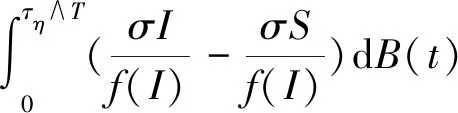
所以有
E[V(S(τη∧T),I(τη∧T)) ]≤V(S(0),I(0))+MT
(11)
设Ωη={τη:τη≤T}, 由P{τη≤T}≥ε知P(Ωη) ≥ε, 且对每个ω∈Ωη,由停时的定义知,在S(τη∧T),I(τη∧T) 中, 至少有一个等于η, 所以
根据(11)式有
令η→0, 则有∞>V(S(0),I(0))+MT=∞, 矛盾. 所以τ0=∞,a.s., 即系统(8)存在全局唯一正解.
2 疾病的灭绝
本节主要讨论在白噪声是一个均值回复过程下疾病的灭绝, 定义系统(8)中ξ=0时的基本再生数
定义系统(8) 的随机基本再生数为:
定理2 如果
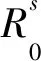
(12)

(13)

(14)
对(14)式从0→t积分, 有
(15)

记

则有
显然
(17)

是一个局部鞅, 根据鞅的强大数定理[15]知
(18)



(19)
根据(16),(17),(18),(19)有



(20)
此时, 根据(16),(17),(18),(20)有

所以疾病灭绝, 从而定理得证.
3 结论