解析几何初步中的思想方法探究

☉江苏省宜兴市官林中学 吴燕江

☉江苏省宜兴市官林中学 李俊峰

解数学题时，若方法得当，则事半功倍；若方法不当，则前功尽弃，做解析几何题更是如此.那么在解析几何中有哪些基本的思想方法，能让我们顺利地将运算进行到底呢？

一、方程思想

解析几何主要是研究曲线与方程的关系，因此求解解析几何问题时，往往离不开方程的思想.

例1已知圆O的方程为x2+y2=1，它与x轴交于P，Q两点，M是圆O上异于P，Q的任意一点，过点A（3，0）且与x轴垂直的直线为l2，直线PM交直线l2于点P′，直线QM交直线l2于点Q′.求证：以P′Q′为直径的圆C总经过定点，并求出定点的坐标.

解析：对于圆O的方程x2+y2=1，令y=0，得x=±1，即P（-1，0），Q（1，0）.

又直线l2过点A且与x轴垂直，所以直线l2的方程为x=3.

又s2+t2=1，故整理可得

若圆C经过定点，只需令y=0，从而有x2-6x+1=0，解得

点评：以P′Q′为直径的圆C是动圆，将动圆的方程改写为曲线系的形式，通过解方程组进而得到定点的坐标.

二、函数思想

对于一类解析几何中的最值问题，往往可以通过构造目标函数，从而转化为求函数的最值问题.

例2（1）点P（1，2）和圆C：x2+y2+2kx+2y+k2=0上的点的距离的最小值是______.

解析：（1）将圆的一般方程化为标准方程为（x+k）2+（y+1）2=1.

所以圆心C的坐标为（-k，-1），半径r=1.

又（1+k）2+（2+1）2＞1，所以点P（1，2）在圆外.

所以点P和圆C上的点的最小距离dmin=|PC|min-r=3-1=2.故填答案：2.

（2）设P（2t，t），则|PA|2+|PB|2=（2t-1）2+（t+1）2+（2t-2）2+（t-2）2=10t2-14t+10，

点评：利用函数关系求解析几何中的最值问题，易错点是容易忽视参数的取值范围.在本例中，参数k与t的取值范围都是任意实数.

三、数形结合思想

解析几何的本质就是用“数”去研究“形”，因此在求解解析几何题时，数形结合是最行之有效的方法之一，尤其对于某些位置关系中的最值（取值范围）问题，往往可以“秒杀”.

例3（1）设圆（x-3）2+（y+5）2=r2（r>0）上有且仅有两个点到直线4x-3y=2的距离为1，则圆的半径r的取值范围是（ ）.

A.（4，6） B.［4，6） C.（4，6］ D.［4，6］

（2）已知圆C1：x2+y2=4和圆C2：x2+（y-8）2=4，直线y=在两圆之间穿过，则实数b的取值范围是_____.

解析：（1）圆心（3，-5）到直线4x-3y=2的距离为d=，而到直线4x-3y=2的距离为1的轨迹为4x-3y=7或4x-3y=-3.

如图1所示，当圆与直线4x-3y=7相交且与4x-3y=-3相离时，圆上只有两点到直线4x-3y=2的距离为1.所以4＜r＜6.故答案选A.

图1

图2

当直线与圆C1相切时，解得b=±3.

当直线与圆C2相切时，，解得b=5或b=11.

由图可知3＜b＜5.故填答案：（3，5）.

点评：化动为静，找到圆或直线的两个特殊位置，很容易从图中看出答案.本例若脱离图形去分析问题，往往理不出头绪，而利用图形，答案可“秒杀”，由此可见，数形结合具有“神奇功效”.

四、等价转换

转化是数学解题的“主旋律”.挖掘目标函数的几何意义，将最值问题等价转化为解析几何中的有关位置关系问题，同时也体现了数形结合的思想.

例4（1）已知点P（x，y）是圆（x+2）2+y2=1上任意一点，则x2+y2的最大值和最小值分别是______.

（2）已知实数x，y满足x2+y2=1，则的取值范围是______.

解析：（1）设t=x2+y2，则t表示圆（x+2）2+y2=1上的点与原点的距离的平方.而此圆的圆心到原点的距离为2，所以tmax=（2+r）2=（2+1）2=9，tmin=（2-r）2=（2-1）2=1.

所以x2+y2的最大值为9，最小值为1.故填答案：9，1.

（2）如图3所示，设P（x，y）是圆x2+y2=1上的点，则表示过P（x，y）和Q（-1，-2）两点连线的直线的斜率.过点Q作圆的两条切线QA、QB，由图可知QB⊥x轴，故kQB不存在，且kQP≥kQA.

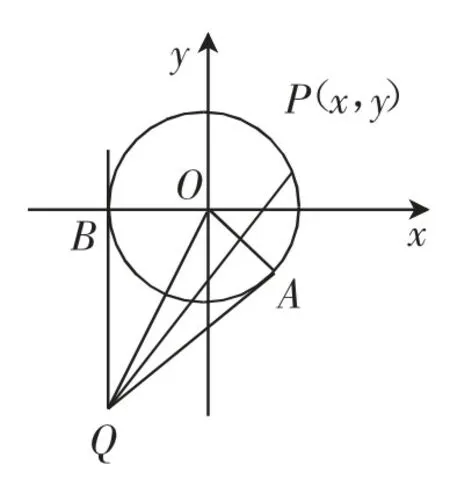
图3

设切线QA的斜率为k，则其方程为y+2=k（x+1），

五、设而不求

我们知道在求解解析几何问题时，解方程或解方程组是“家常便饭”，而为了优化解题过程，我们往往需要对方程组的解或相关点的坐标“设而不求.”

例5已知圆x2+y2+x-6y+m=0与直线x+2y-3=0相交于P，Q两点，O为原点，且OP⊥OQ，求实数m的值.

解析：由消去y得5x2+10x+4m-27=0.

设P（x1，y1），Q（x2，y2），则

又因为OP⊥OQ，所以kOP·kOQ=-1，即x1x2+y1y2=0.

整理可得5x1x2-3（x1+x2）+9=0，

解得m=3且满足Δ>0，所以实数m的值为3.

点评：此题设出P，Q两点的坐标，但在求解的过程中又不刻意地求出来，只将其作为一个转化过程中的桥梁，这种“设而不求”的解题方法在解析几何中很常见，要注意认真体会并掌握.

本文最后值得一提的是，所谓解析几何就是用代数的方法来解决几何的问题，所以善于运算是解题的关键，而如何优化运算是一个值得研究的问题，或许本文会对大家有所启发.