“稚化思维”下的数学解题教学

☉江西省赣州中学 谢小翔

数学离不开解题，但解题教学很容易异化为教师展示“特技”的舞台.台上教师“精彩纷呈，滔滔不绝”，台下学生“瞠目结舌，顶礼膜拜”.教师成了“演员”，学生自然只能充当“观众”，解题教学就很容易陷入“懂而不会”、“会而不对”的怪圈.其实，成功的解题教学追求的是“深入浅出”.诚然，教师的解题能力决定教学能否做到“深入”，而教师的教学水平则决定了在“深入”的基础上能否实现“浅出”.只有“深入”而不能“浅出”的解题教学充其量只能是“纸上谈兵”.因此，教师是否具备“稚化思维”的意识，能否采用“稚化思维”的策略开展课堂教学是检验教师教学水平的重要依据.

一、“蹲下身”，惑学生之所惑

学生的思维方式是教师进行教学设计的出发点，教师不要单纯地以自己假想的问题和经验作为解题教学的主要依据，而是要“蹲下身来”，立足学生的真实问题和已有经验，思考学生可能出现的“困惑”，然后把这些“困惑”作为教学的出发点，从而“惑其所惑，疑其所疑”，帮助学生从原有的知识和经验中寻找知识的生长点.

问题：如图1，已知抛物线C的方程为x2=4y，F为其焦点，过不在抛物线上的一点P作抛物线的切线PA，PB，A，B为切点，且PA⊥PB.

（1）求证：直线AB过定点；

意图：一方面，通过本题能够引出上课的主题，激发学生的求知欲；另一方面，通过学生的尝试解答，暴露学生思维，发现存在的问题.

对于本题，全班的得分非常不理想，系统分析后，发现存在以下几个问题：

图1

先让学生尝试解答，然后进行错误分析，进而发现学生存在的“真问题、实问题”，这为教师“站在学生认知水平稚化解题思维”搭建认知“脚手架”提供数据支撑.

二、“退一步”，难学生之所难

华罗庚曾经说过：“善于‘退’，足够地‘退’，‘退’到最原始而不失重要性的地方，是学好数学的一个诀窍.”教师的“退”一方面有助于教师进行换位思考，体会到学生的困难所在，以学生实际的思维方式为基点来进行教学设计；另一方面能缩小师生之间思维与认知的“差距”，从而有助于实现教师思维的“学生化”，促进教与学过程的自然融合.

不难发现，以下几个“难点”对学生的解题造成了极大的困扰.

难点1：“已知抛物线上一点，求在这点的切线方程”.直接“求导”或者利用“Δ法”，需要耗费大量的时间.如何能够让学生快速地写出此类切线方程是解决问题的关键.我们不妨先从学生的已有认知入手，学生已经掌握了“求过圆上一点的切线方程”的方法，通过类比就容易得到过椭圆与抛物线上一点的切线方程.

难点2：“切线PA、PB与切点弦AB之间到底有什么关系？”可以从“圆的切线与切点弦”入手，然后把研究的结论类比到抛物线上，这样学生就很容易理解问题的真相到底是什么.

设P（x0，y0）是圆外一点，两条切线分别为PA、PB，A（x1，y1），B（x2，y2）为切点，则因为P是两条切线的交点，所以P也满足切线方程.代入切线方程得由此可见，A，B两点所表示的坐标是方程xx0+yy0=r2的解，所以切点弦AB的方程就是xx0+yy0=r2.

容易发现，从结构上看，切线与切点弦所在的直线是“同一个”，关键是看（x0，y0）在曲线上还是外.

运用上述结论，本题的第（1）问就很容易解答.设P（x0，y0），A（x1，y1），B（x2，y2），则直线AB的方程为xx0=2（y+y0），把它和抛物线方程x2=4y联立得x2－2xx0+4y0=0⇒x1+x2=2x0，x1x2=4y0；易得，因为PA⊥PB，所以x1x2=－4，y0=－1，即直线AB恒过（0，1）点.

教师在难点处，不妨表现出“一筹莫展”的样子，从而吸引学生的注意力，引发学生的深度思考，继而在后续的探究中逐步发现高招，和学生一起破难、解难，直至最后师生共品胜利的果实.

三、“装糊涂”，错学生之所错

由于认知障碍、理解偏差和思维习惯等方面的原因，学生难以避免地会犯一些知识性、方法性和“想当然”的错误.对学生而言，“犯错”并非是坏事，“错误”有助于教师更好地了解学生的思维，甚至是很多学生必须要经历的思维阶段.因此，教师可以适当进行“模拟”，“装糊涂”一下，沿着学生的思路，故意和学生“一起犯错”，然后再回过头来正视这一错误，引导学生识别错误，或者借助错误故意挑起“争端”，通过争论实现纠错，从而实现在强化错误根源认识的基础上提升学生在数学认知上的“免疫力”.

第（2）问在计算上故意设置“障碍”，学生会想当然地去直接求.思路很简单，先求R点的坐标，再把R点坐标用（x0，y0）表示出来，最后代入，这种方法可行吗？

由于学生预先不知道可以通过“切线与切点弦”之间的关系得到y0=－1这个结论，从而导致参数太多，望而生畏；就算使用了y0=－1这个结论，其中的运算也很复杂，要获得正确的答案也并非易事.

既然此路不通，教师就可以顺势引导学生另辟蹊径.发现直线AB过焦点F可以转化为，又因为PF⊥AB，即，则，易得，本题迎刃而解.

教师“以身试错”不仅有助于学生减少错误，而且有助于学生在尝试中发现正确的解题思路.关于这一点，著名的华裔数学家萧荫堂就说的很好，他指出“有时教授备课不足，笨手笨脚地算错了数，从他搔着手、念念有词的改正中，反而可以看出他的思路，真正学到些东西.”因此，教师故意犯错并非坏事，其价值就是教师抛错误的“砖”，从而引出学生的“玉”.

四、“深探究”，促进学生思维“智化”

在数学解题教学中，学生在教师的指导下，不断地经历类似专家的思维过程，从而促使自己的认知结构向专家认知结构的嬗变.教师“稚化”自己的思维有助于师生之间保持认识程序上的“同频”，从而更容易引发教与学的思维“共振”，其最终目的是为了实现学生思维的“智化”.因此，在师生思维“同频、共振”的基础上，进一步深入探究题目背后的数学原理是实现学生的思维走向“智化”的关键.

解决此题的关键是要“发掘P点与直线AB之间的联系”.以类似“△PAB”为背景的问题在考试中经常出现，这就是所谓的“阿基米德三角形”.“阿基米德三角形”，即圆锥曲线的弦与过弦的端点的两条切线所围成的三角形.它有很多非常有用的性质，毫不夸张地讲，阿基米德三角形就是解题的利器，在解题中可以起到事半功倍的效果.

例（2019年高考全国卷Ⅲ理科第21题）

（1）证明：直线AB过定点；

本题的背景正是“阿基米德三角形”，结论是阿基米德三角形性质的一个特例：如图2，过抛物线的准线上一点D引抛物线的两条切线DA，DB，则切点弦AB必经过抛物线的焦点.

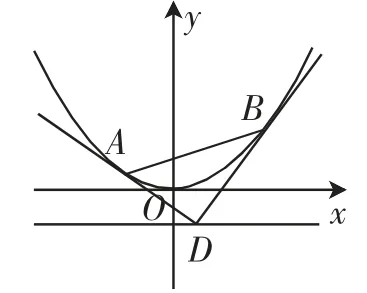
图2

“稚化思维”并非降低教学要求，弱化思维能力，其目的是通过“稚化”来实现教与学的共振，从而实现从“稚化”到“智化”的飞跃，最终使得数学解题摆脱“就题论题”的局限性，实现“解一题，会一类，通一片”的教学目标.