利用一道课本习题 简解并推广一道高考试题
(邮编:432000)
湖北省孝感高级中学
课本是最重要的教学资源,也是学生学习的出发点,根据地.如何充分挖掘课本习题的丰富内涵,揭示解题思想,渗透核心素养,并利用它解决新问题,是数学教师重要的课题.开展课本典型问题的研究性学习,不但有利于引导学生在高考复习中重视课本的再学习,而且可以让学生看到课本题与高考题之间内在的联系,让学生消除对高考试题的神秘感,帮助学生学会思考,看清问题的本质.本文结合教学实践,研究课本中的一个习题,并利用它简解一道2019年北京高考理科试题,以期对如何高效组织高考复习有所启迪.
1 课本习题解答
《普通高中课程标准实验教科书数学必修2》第124页第5题是:已知圆的一条直径的端点分别是A(x1,y1),B(x2,y2),求证此圆的方程是(x-x1)(x-x2)+(y-y1)(y-y2)=0.

(x-x1)(x-x2)+(y-y1)(y-y2)=0.
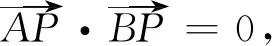
从以上两种解法可以看出,直接法单刀直入,需要将圆的标准方程利用因式分解得到最终结论;而利用轨迹思想求圆的方程,曲径通幽,可有效减少运算量.通过本题的解答可以得到一个实用的结论.
2 结论的应用
(2019北京卷理科18题)已知抛物线C:x2=-2py经过点(2,-1),(1)求抛物线C的方程及其准线方程;(2)设O为原点,过抛物线C的焦点,作斜率不为0的直线l交抛物线C于两点M、N,直线y=-1分别交直线OM、ON于点A和B,求证:以AB为直径的圆经过y轴上的两个定点.
解析(1)C的方程为x2=-4y,准线方程为y=1(过程略).
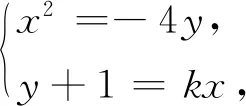
得x2+4kx-4=0,
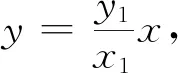

令x=0,则(y+1)2=4,解得y=1或-3,故以AB为直径的圆经过y轴上的两个定点(0,1)和(0,-3).
点评本题虽然是一个定点问题,但是利用课本上的结论,缩短了解题的思维流程,简洁明了,比参考答案要简洁的多.本题易推广得到如下结论:
3 高考试题的推广
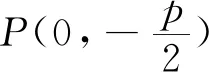
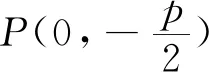
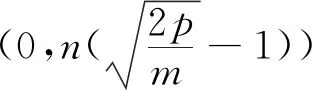
证明设直线l的方程为y+m=kx(k≠0),M(x1,y1),N(x2,y2).
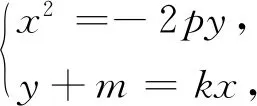

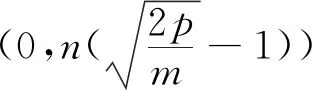

证明设直线l的方程为x-m=ty,M(x1,y1),N(x2,y2).
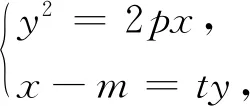


4 一点感悟
从以上可以看出,教材是数学能力与思想的载体,教师要引导学生扎根教材,用好课本.课本是命题的源泉,也是解决问题的依据;另外课本是几代人集体智慧的结晶,它具有相当完备的知识体系和能力架构系统,其中的例题和习题是学生解题能力的核心生长点,开展课本典型例习题的研究性学习有利于减轻学生的负担,使学生跳出题海,起到事半功倍的效果.随着数学核心素养的理念不断强化,新高考改革不断推进,将来不分文理科的趋势逐渐形成,相信会有更多的高考题取材于课本,经过加工改造后又高于课本,这能充分体现高考命题依纲靠本,源于教材又高于教材的指导思想.

