基于粒子群优化极限学习机的风功率预测

赵睿智， 丁云飞

(上海电机学院 电气学院， 上海 201306)

风的随机性和波动性导致了风电功率的不平稳性，风电场的接入影响电网的稳定运行环境[1]。对风电场的输出功率进行精准预测，有助于电网人员根据风电场输出功率的变化调整发电计划，减少电网的备用容量以节约能源的消耗。因此，有效的风电功率预测方法可保障电网的稳定经济运行。

目前，国内外研究人员做了大量的工作，研究方法主要包括物理方法、统计方法以及神经网络方法[2]。其中物理方法要求风机相关物理信息，建模复杂且精度不稳定。统计方法模型简单、数据单一，但预测的精度受时间的限制，预测时间越长精度越低，通常应用于超短期预测。神经网络方法泛化能力强，能够处理回归问题，适用于风功率预测。

极限学习机(Extreme Learning Machine, ELM)是一类基于前馈神经网络的算法[3]。ELM因结构简单、学习效率高，被用以解决回归、聚类、分类等问题。ELM算法的优化问题被很多学者研究，王浩等[4]利用遗传算法优化极限学习机，并将风电系统参数模糊化，从而提高预测模型的精度。龙浩[5]提出了加权极限学习机方法，旨在解决样本数据不均衡的问题。王文锦等[6]利用蜂群算法优化ELM，旨在提高模型的稳定性能。王宏刚等[7]将蜻蜓算法(Dragonfly Algorithm, DA)分布式应用于ELM，优化初始化输入权重和阈值的影响，有效提高了电能质量扰动识别率。

风电功率的预测主要基于当日的数值天气预报信息(Numerical Weather Prediction, NWP)。NWP包括风速、风向、温度、湿度以及气压[8]。实测NWP数据在同一风功率下存在奇异值以及波动的问题。关于风功率NWP数据的预处理问题，符杨等[9]针对NWP数据不准确、爬坡事件频发等原因将NWP数据分类，并对功率波动进行预测。杨茂等[10]利用经验模态分解对风功率数据进行分解去噪重构，一定程度上减少了噪点对预测结果的影响。杨家然等[11]利用模糊聚类的方法将原始信号进行分类，采用不同的模型组合预测。

本文将粒子群优化算法(Particle Swarm Optimization, PSO)和ELM结合，欲提高传统ELM预测模型的精度和稳定性能，从而为风电功率预测技术提供新的方法。

1 基本理论

1.1 ELM算法

ELM因学习效率高被普遍应用于风电功率预测、变压器故障诊断、风机故障诊断等方面。该算法任意赋值输入层权重和阈值，训练过程中无需改变模型参数，仅设定隐层神经元个数，便可通过最小二乘法获得输出层权重。

现简述ELM模型的算法步骤:假设N个训练样本(xi,ti)，其中xi=[xi1,xi2,…,xin]T，表示n维训练样本。ti=[ti1,ti2,…,tim]T，表示m维学习样本。设定网络含有L个隐含层神经元，激励函数为g(x)的ELM模型为

(1)

式中:βi为隐含层第i个节点与输出层节点的权重；wi为输入层节点与隐含层第i个节点的权重；bi为第i个隐含层节点的阈值；oj为网络的实际输出值。

若L=N，具有L个隐含层神经元网络的输出值可以逼近N个训练样本，即

(2)

式(1)可表达为

(3)

式(3)可用矩阵形式表达为

Hβ=T

(4)

式中：H为隐含层输出矩阵。

(5)

当N足够大时，ELM的输出误差逼近一个任意值ε>0，β可通过最小二乘法求解，得

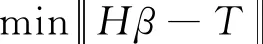
(6)

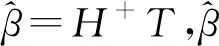
1.2 粒子群算法

PSO来源于对鸟群觅食的探索[12]。其主要思想:将目标的寻找范围比作鸟群的飞行范围，鸟被抽象化为粒子，每个粒子可视为寻找目标的个体，粒子的位置作为目标的潜在位置，粒子的飞行过程作为个体的寻找过程。粒子的属性为位置和速度，该属性决定了搜寻的方向和快慢。每个粒子独自寻找的最佳位置叫个体极值，群体中最佳的个体极值视为全局最优解。粒子的速度取决于自身经验及群体经验。D维空间中第i个粒子的速度和位置分别为

Vi=[vi,1,vi,2,…vi,D]

Xi=[xi,1,xi,2,…xi,D]

在每次迭代中，确定每个粒子所经过的最佳位置Pb以及群体所发现的最佳位置Gb。通过不断更新Pb和Gb，依据式(7)和式(8)更新粒子的两个属性，最终找到全局最优位置

vi,j(t+1)=w·vi,j(t)+c1r1[Pi,j-xi,j(t)]+

c2r2[Gj-xi,j(t)]

(7)

xi,j(t+1)=xi,j(t)+vi,j(t+1),j=1,2,…,N

(8)

式中：c1和c2为学习因子，分别表示个体学习因子和社会学习因子；r1和r2为0到1之间的随机数；w为惯性因子，通过调整w的大小可对寻优性能进行调整。

2 基于PSO-ELM的风功率预测模型

2.1 NWP数据预处理

在风功率预测模型中，NWP数据包括前一时刻风速、当前时刻风速、风向正弦、风向余弦、温度、湿度、气压。NWP数据预处理步骤:首先剔除NWP数据中的异常数据，并根据实际数据进行插值补全，将处理后的NWP数据进行归一化处理，将处理后的NWP数据分为不同组进行训练与预测[13]。

2.2 PSO-ELM预测模型

如前文所述，ELM的初始输入权值和阈值是随机确定的，其训练的效果会受初始值影响。因此，采用PSO优化ELM的输入权重和阈值，可避免盲目性训练ELM模型。PSO算法优化ELM的步骤中，先初始化PSO参数，包括粒子群的规模、空间维度、惯性参数w、学习因子c1和c2、迭代次数和最大速度vmax等。PSO-ELM预测模型是将每个粒子对应的输入权值和阈值代入ELM预测模型中，将ELM学习样本输出与实际输出的均方误差(Mean Squared Error, MSE)作为PSO的适应度。将粒子的当前适应度与最优适应度做对比，若比最优适应度小，说明当前输入权值和阈值所建立的ELM模型进行预测产生的均方误差较小，则将当前适应度更新为最优适应度，将当前位置更新为Pb，否则保持最优适应度不变。同理比较适应度和全局适应度，更新Gb。当迭代次数达到最大值或适应度达到设定值时停止算法。PSO优化得到的最优输入权值W和阈值b后，代入 ELM模型中进行预测。具体步骤如图1所示。

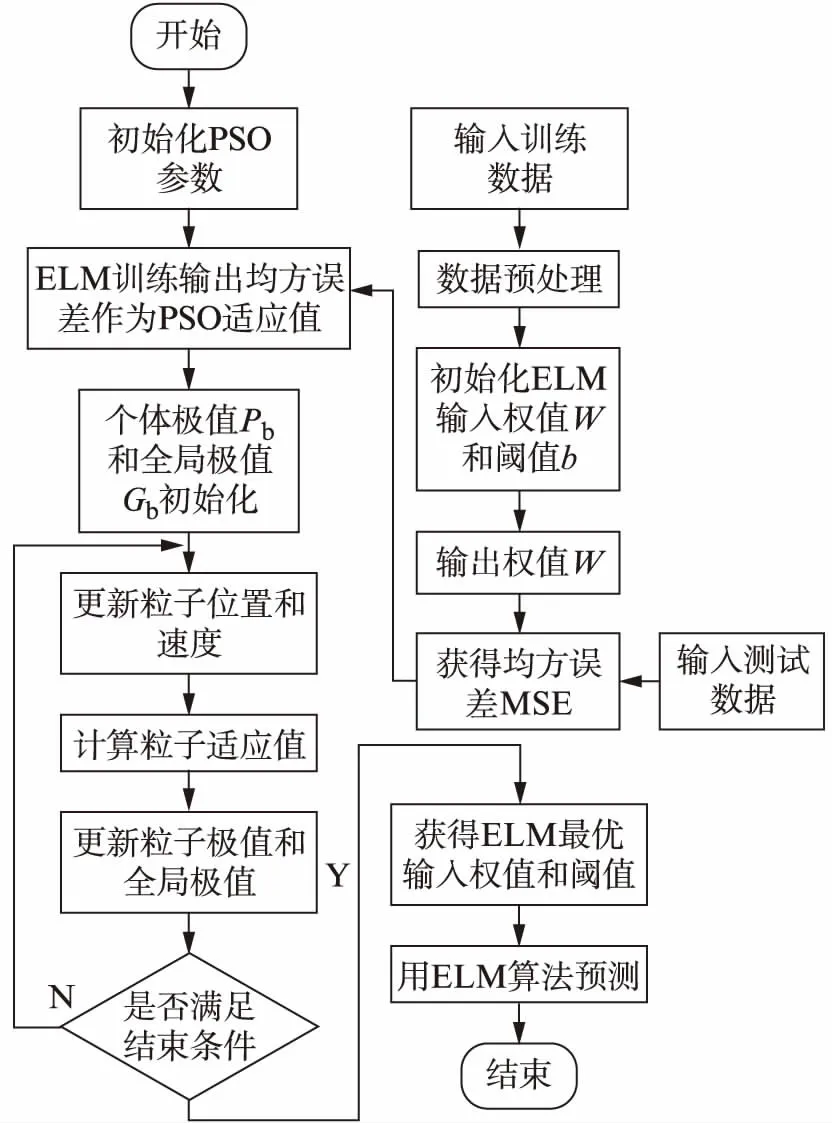
图1 PSO-ELM算法流程图

2.3 基于NWP和PSO-ELM的风功率预测模型

将NWP数据按时间序列分为训练集D1、测试集D2、预测集D3。将训练集D1代入PSO-ELM模型中训练。用测试集D2代入PSO-ELM中获得预测均方误差MSE，将MSE作为粒子群的适应度，经过不断迭代建立起基于PSO-ELM预测模型。将预测集D3代入模型中预测。具体模型框架如图2所示。

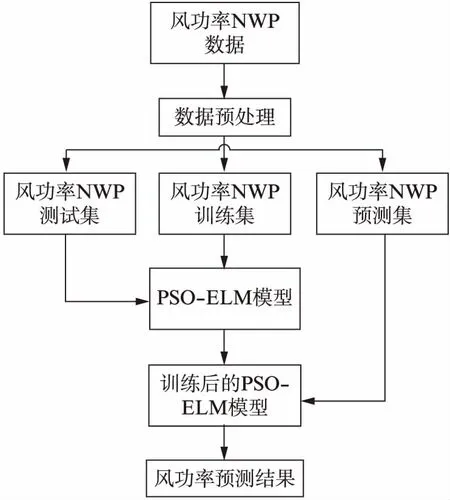
图2 基于NWP和PSO-ELM的风功率预测模型框架

2.4 评价指标

为了验证模型的效果，本文分别以绝对平均误差(Mean Absolute Error, MAE)、相对百分误差绝对平均值(Mean Absolute Percentage Error, MAPE)和均方根误差(Root Mean Square Error, RMSE)作为评价指标来验证预测效果[14]。

(13)

(14)

(15)

式中：EMAE为绝对平均误差；EMAPE为相对百分误差绝对平均值；ERMSE为均方根误差；et为预测绝对误差值，et=Rt-Yt(其中Rt为 第t个风电功率实测值；Yt为第t个风电功率预测值)；m为预测时间点数。

3 实验与结果分析

3.1 数据来源

本实验以华东地区3个风电场的NWP数据为例进行风功率的预测。3个风电场的装机容量分别为50 MW、70 MW和100 MW。以50 MW风电场作为本文的主要展示对象，其功率时序曲线见图3。NWP数据共7维，分别包括前一时刻风速、当前风速、风向正弦、风向余弦、温度、湿度、气压。风电场抽样周期为1 h。

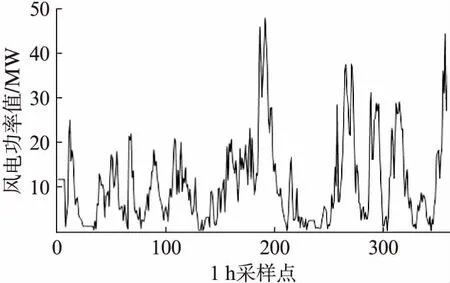
图3 50 MW风电场功率时间序列

3.2 参数设定

在Matlab R2016a运行平台中，PSO-ELM模型的参数设定如下:输入层节点个数为7；隐含层节点个数为12；输出层节点个数为1；激活函数选择Sig函数。粒子群的迭代次数为150，惯性因子W在迭代过程中由0.8递减至0.4。学习因子与PSO-ELM模型训练效果密切相关，本实验选择了4种待定PSO学习因子情况Y1，Y2，Y3，Y4，如表1所示。

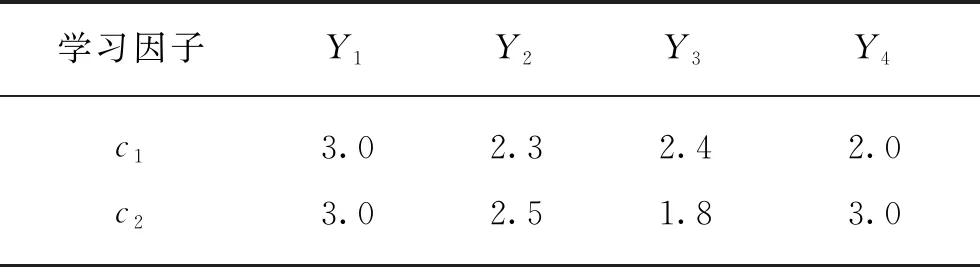
表1 PSO学习因子参数设定

训练后PSO-ELM的最优适应值变化如图4所示。比较4种情况的最优适应值迭代变化曲线。c1=3.0，c2=3.0以及c1=2.0，c2=3.0两种情况的均方误差较大；c1=2.3，c2=2.5时收敛速度慢且均方误差达不到最小；c1=2.4，c2=1.8时收敛速度快且均方误差最小。因此，选择第3种参数建立PSO-ELM模型。

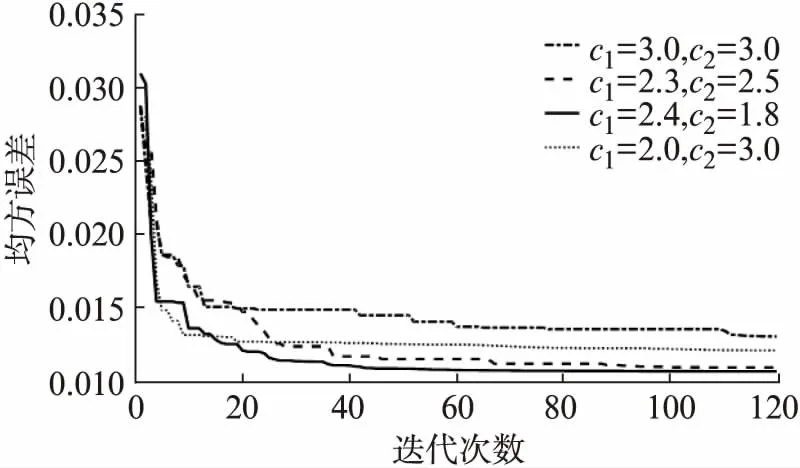
图4 PSO-ELM最优适应值变化迭代图

3.3 PSO-ELM预测结果对比

图5～图7分别给出了50 MW、70 MW、100 MW风电场的PSO-ELM模型风功率预测曲线图。50 MW、70 MW和100 MW的PSO-ELM预测曲线与真实曲线拟合程度高且趋势相同。图5～图7中PSO-ELM预测曲线没有剧烈的波动和偏差。因此，PSO-ELM模型具有良好的泛化性能，相比较于传统的ELM模型有较大的改善。

采用ELM模型、支持向量机(Support Vector Machine, SVM)模型、BP模型以及PSO-ELM模型分别对50 MW、70 MW、100 MW风场的风功率数据进行建模分析。其中SVM的惩罚系数C和核参数γ分别取30和0.731 7，BP和ELM模型的隐含层节点个数分别取8和5。由表2可知，PSO-ELM模型相比于BP、SVM、ELM模型在不同风场的NWP数据中预测精度最高，表明本文提出的方法具有普适性。在50 MW风场中，PSO-ELM的EMAE、ERMSE、EMAPE相比于ELM分别降低了39.24%、32.87%、32.03%。在70 MW风场中，PSO-ELM的EMAE、ERMSE、EMAPE相比于ELM分别降低了47.54%、24.72%、38.12%。在100 MW风场中，PSO-ELM的EMAE、ERMSE、EMAPE相比于ELM分别降低了26.59%、31.06%、29.33%。说明PSO算法对ELM输入权值和阈值进行优化可以提高ELM模型的预测精度。

图5 50 MW风电场功率预测曲线

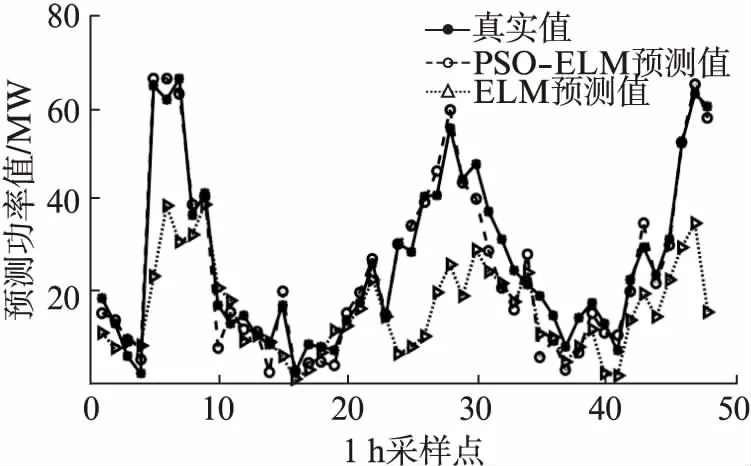
图6 70 MW风电场功率预测曲线

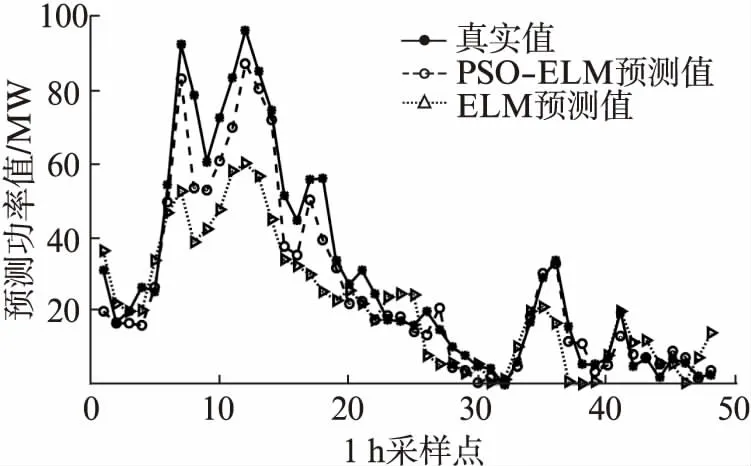
图7 100 MW风电场功率预测曲线

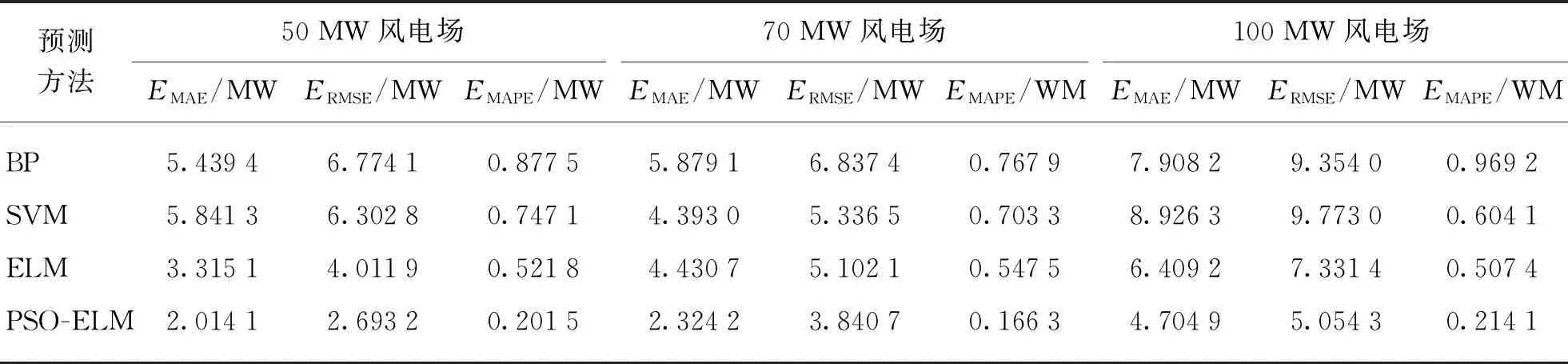
表2 不同风电场的预测结果

4 结 语

本文针对风电功率的波动性和间歇性等问题，提出了基于NWP和PSO-ELM的预测方法对华东地区3个不同装机容量的风电场功率进行预测。首先将NWP预处理，获取与风功率有关的天气信息数据；再采用PSO算法优化ELM以确定ELM的输入权重和阈值；最后通过预测3个风电场的功率验证此方法的普适性。实验表明，本文方法所建立的PSO-ELM模型对风电NWP数据的预测效果优于传统ELM模型。