中低压网无功补偿优化方案设计

吴 星， 刘天羽

(上海电机学院 电气学院，上海201306)

进入21世纪以来，电力系统无功优化一直是电力系统规划的重要课题，以最经济的投资保证电力系统维持合理的电压水平、降低系统网损、提高线路传输能力以及实现系统安全平稳运行是电力系统无功优化的最终目的。文献[1]采用本德(Benders)分解技术把无功优化问题分解成投资与运行两个问题；文献[2]提出了采用基于降损收益分析的启发式方法；文献[3]提出了一种新的图形搜索方法。

本文提出了中低压配电网的无功优化方案，分析其他优化算法在求解过程中出现的局部最优、搜索能力较弱等缺陷，采用改进的带精英策略的快速非支配排序遗传算法(Nondominated Sorting Genetic Algorithm Ⅱ, NSGA2)[4]对中低压网无功问题进行优化求解，验证了方案的有效性。

1 无功补偿优化方案

1.1 目标函数

针对中低压网无功补偿存在的问题特点，将无功补偿容量F1和负荷节点电压偏差F2最小作为无功优化目标函数，数学模型为

(1)

式中：QC为中低压网无功补偿总容量；ΔUL为负荷节点电压偏差；N1为无功补偿装置(Static Var Compensatar, SVC)的补偿点个数；NL为负荷节点个数；QCi为节点i的补偿容量；Ul为所在节点的真实电压；Ul0为所在节点的预期电压；ΔUlmax为所在节点的允许电压偏差最大值。

1.2 无功优化约束条件

潮流等式约束为

(2)

式中：PLi为节点i的有功功率；QLi为节点i的无功负荷功率；ΔQCi为补偿节点i的电容器补偿功率；Gij、Bij为节点导纳矩阵中第i行第j列对应元素的实部虚部；Nn为节点总数[5]。

不等式约束条件为

(3)

式中：QCimin为无功补偿节点i的无功补偿容量最小值；QCimax为无功补偿节点i的无功补偿容量最大值；N1为SVC的补偿点个数；Timin为第i个有载调压变压器变比的最小值；Timax为第i个有载调压变压器变比的最大值；Ti为第i个有载调压变压器的变比；N2为有载调压变压器的个数；Uimin为中低压网内部节点i电压的最小值；Uimax为中低压网内部节点i电压的最大值；Ui为中低压网内各个节点i电压的大小；N3为负荷节点的个数[6]。

1.3 无功补偿点确定

本文将使用电压稳定模态分析方法[7]来确定中低压网无功补偿点。通过对系统的静态模型进行计算分析，得到的参数值能正确反映出中低压网各个节点的电压稳定程度。

线性化的中低压网功率电压方程为

(4)

式中：ΔP为中低压网内节点的有功微增量；ΔQ为中低压网内节点的无功微增量；JPφ、JPγ、JQφ、JQγ为计算中低压网潮流雅可比矩阵所得到的子矩阵；Δφ为中低压网内节点电压相角的微增量；ΔU为中低压网内节点电压幅值的微增量。

对式(4)中的ΔP取值为零，令JJH=MλNT，则可得

(5)

式中：JJH为中低压网系统简化的雅可比矩阵；λ为中低压网系统简化的雅可比矩阵JJH的特征矩阵；N、M为中低压网系统简化的雅可比矩阵JJH左右特征向量形成的模态矩阵[6]。

因此，式(5)中的ΔU可以转化为

(6)

式中：Mi为中低压网系统简化的雅可比矩阵JJH的第i列的右特征向量；Ni代表中低压网系统简化的雅可比矩阵JJH的第i列的左特征向量。

1.4 模糊权重处理

通过优化算法得到的一系列帕雷托(Pareto)解往往并不是目标最优解，而是满足约束条件下的解的集群，无法同时达到最优[8]。本文采用模糊权重[13]的处理方法对此进行优化。每个中低压网对无功优化的要求标准都有侧重点，根据侧重点的不同来对目标函数分配相应的模糊权重，其数学模型为

(7)

式中：F为中低压网无功优化方案所求目标函数；λi为模糊权重系数；τ(Fi)为对各个目标函数进行模糊化处理的函数；Fi(处理值)为目标函数进行模糊权重处理所使用的处理值。

2 NSGA2

2.1 交叉算子改进

NSGA2中采用的是交叉算子(Simulated Binary Crossover, SBX)。但是使用SBX交叉过程中搜索能力较弱，无法保证种群的多样性[9]，所以通常情况下一般实数编码都引入算数交叉算子[10-11]，有

(8)

式中：α、β为算数交叉算子交叉参数，α+β=1，α,β∈[-1,2]且均匀分布。

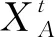
2.2 变异算子改进

2.2.1 新变异算子提出 在遗传算法中，变异算子是作为背景算子提出。在算法中引入变异算子，其局部随机搜索性能会有所增强，向最优解收敛的速度会加快并可以保证解群的多样性[12]。

差分进化算法(Differential Evolution, DE)是一种全局优化算法，基于群体的启发式搜索，它是由Storn等[12]在1995年提出，具有记忆个体最优解以及受控参数少的特点。差分进化算法与传统的进化算法相比，前者引入一种特殊的变异算子，能对被选中个体的进化方向产生扰动，对寻找最优解有一定优势[13]。本文针对NSGA2变异机制的不足进行改进，利用差分进化算法中的变异思想，提出一种基于质心理论的新变异算子。

质心的计算为

(9)

式中：rδ为质心；mi为第i个粒子的质量；ri为第i个粒子所对应的具体值。

本文将此思想引入到NSGA2算法中的变异阶段，对质心理论的应用做出改进，提出一种基于质心的变异算子，表示为

Xnew(t+1)=γXbest(t)+(1-γ)Xi(t)+

(10)

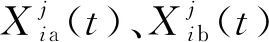
2.2.2 最佳质心个体的选择 对于Xbest(t)的选择，本文引入质心理论的思想，求得的最佳质心个体为

(11)

式中：N为从第t代种群中随机抽取的变异个体总数；fi(t)为对应的Xi个体的适应度值。

2.2.3 扰动向量权重改进 在式(10)中，λ是扰动向量权重[14]，它的选取具有一定随机性，本文中随机扰动借鉴多项式变异有k=rand(0,1)，表示为

(12)

2.3 无功优化步骤

基于本文提出的改进遗传算法，将其运用到中低压网无功优化中，操作步骤如下:

(1) 输入中低压网原始数据；

(2) 对中低压网进行牛顿-拉夫逊潮流计算[15]，得到中低压网的有功网损以及各个节点的电压等初始化数据；

(3) 采用电压稳定模态分析法计算中低压网各个节点的模态值，选择数值较小的节点作为无功补偿候选节点；

(4) 以QCi、Ti作为本文的控制变量，采用实数和整数混合编码[QC1，QC2，…，QCN1|T1，T2，…，TN2]，其中QCi采用实数编码，Ti采用整数编码；

(5) 随机产生初始种群；

(6) 对种群中每个个体进行适应度函数计算；

(7) 按照本文提出的改进型带精英策略的快速非支配排序遗传算法进行选择、交叉、变异等运算操作；

(8) 检验是否满足最大迭代次数，若满足则结束计算，若不满足则返回到(6)重新开始计算。

3 算例分析

为了验证此方案的有效性，本文在Matlab软件中，建立一个具有多条10 kV线路的中低压网系统，见图1。变压器型号选为SL7-250/10，导线型号为LGJ-120，各支路的线路长度见表1。遗传算法参数设置为:种群规模50，最大迭代次数100，交叉概率0.9，变异概率为0.02。采用电压稳定模态分析法对中低压网各个节点进行计算，求解出各个节点的电压稳定模态值(标幺值)，如表2所示。

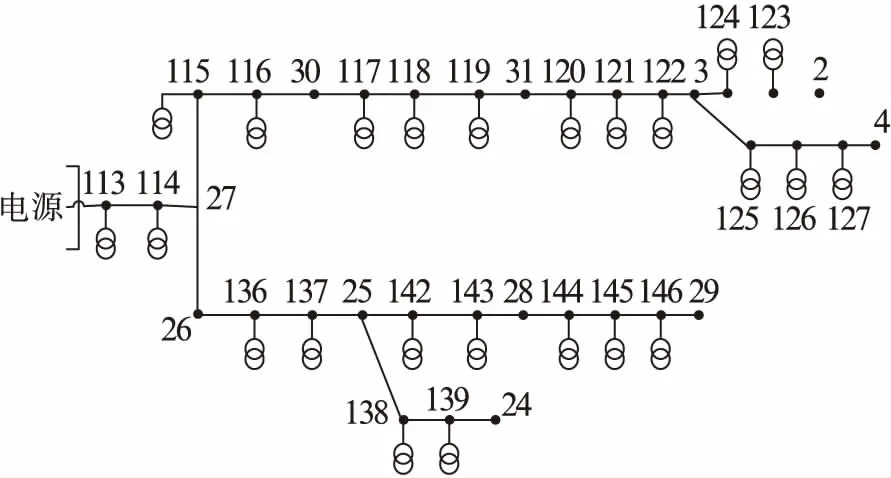
图1 中低压网配电示意图

对比表2数据，节点编号31、144、126的电压稳定模态值最小，即可作为无功补偿点。用牛顿-拉夫逊法对中低压网进行潮流计算，然后采用NSGA2来求解得到配电网的无功补偿容量最少以及负荷节点电压偏差最小的Pareto最优解。无功优化目标函数的Pareto最优解，如表3所示。

表1 中低压网各支路长度

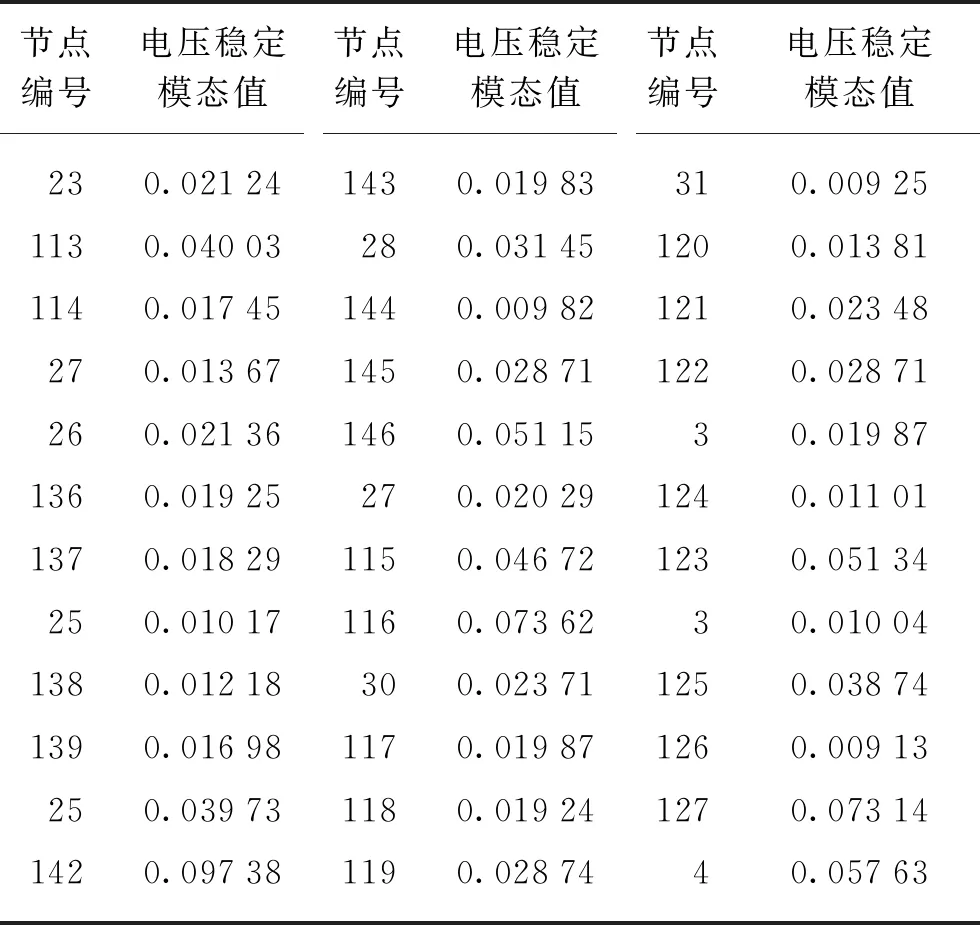
表2 中低压网各节点电压稳定模态值(标幺值)

采用模糊权重处理优化目标函数，对F1赋予最大的模糊权重λ1=0.8，对F2设置λ2=0.2。对于目标函数处理值Fi(处理值)，本文选取目标函数的平均值作为处理值，设置如下:F1(处理值)=23.604 80，F2(处理值)=0.082 857，根据式(8)可得到36个最优解的函数值(见表4)。

由表4可知，第24组解F=0.899 201最小，对照第24组解的数据为:6.122 07、7.867 29、6.920 69、20.910 05，四舍五入取值为6.1、7.9、6.9、20.9，即对节点31、144、126这3个补偿点待

补偿容量分别为6.1 Mvar、7.9 Mvar、6.9 Mvar，总补偿容量为20.9 Mvar。使用SVC对补偿点

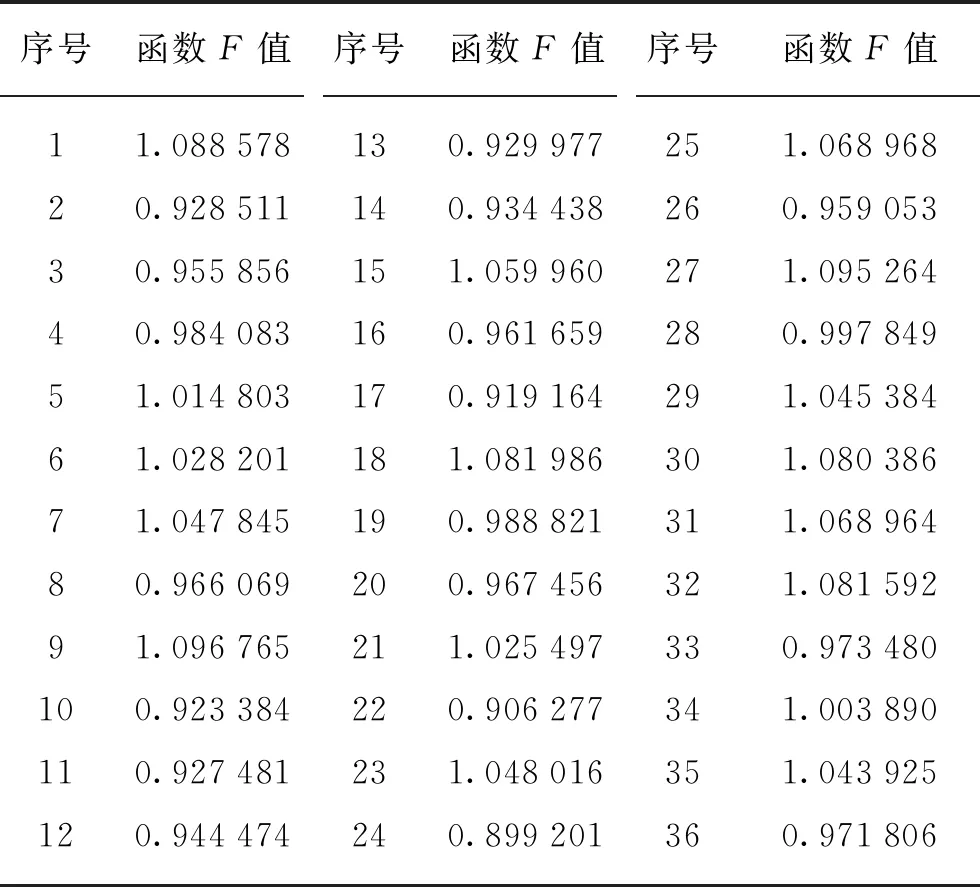
表4 模糊权重处理后的最优解F值

进行无功补偿，则补偿前后各个节点电压值的前后数据，如表5所示。

(续表5)

中低压网的有功网损以及各个负荷节点电压偏差变化情况，如表6所示。

表6 中低压网有功网损与负荷节点电压偏差变化

通过对中低压网算例系统的仿真结果可以看出:进行无功补偿优化后的中低压网有功网损明显较少，负荷节点电压偏差也显著减小，中低压网的电压质量比补偿前更好。算例仿真结果证明了NSGA2应用于中低压网无功优化的有效性以及准确性，本文所提出的方案可以用于处理中低压网无功优化问题。

4 结 语

本文提出了一种基于质心理论的NSGA2算法，并针对中低压网提出了改良的无功优化方案，在中低压网的仿真算例中验证了新算法对于中低压网系统无功优化的有效性，优化结果在中低压网配电系统的电压质量、有功网损以及节点电压偏差上表现性能良好。