基于车间通信的换道策略研究

温永祺 ，谢东繁 ，王祥 ，周豪

(1.北京易华录信息技术股份有限公司，北京 100043；2.北京交通大学交通系统科学与工程研究院，北京 100044；3.成都地铁运营有限公司，四川 成都 610000)

道路交通系统中，车辆的驾驶行为包括两种：跟驰行为和换道行为。其中，换道行为对道路交通流产生较大影响，基于换道模型研究其对交通流影响的内在机理，从而有针对性地提出换道策略，能够减少换道行为对道路交通流的影响。目前相关研究主要分为基于规则的换道模型和基于离散选择行为的换道模型。

基于规则的换道模型是从单个驾驶员的角度模拟车辆换道，首先列举换道原因并评估换道是否适用，然后选择目标车道，最后根据实际数据标定间距接受模型的参数。双车道交通的换道规则又可分为关于车道对称的和不对称的。Nagatani[1]使用完全确定型的规则，研究了双车道交通系统。Knospe等[2]在双车道交通中使用了一套更加复杂的换道规则，该规则重现了限速情况下流量增加的现象。Chowdhury等[3]提出了基于双车道交通的粒子跳跃模型，更加详细地描述了车辆的换道。李珣等[4]提出了一种考虑局部区域车辆状态优化的协同换道模型，研究表明在同等车辆密度下，此规则减少了拥堵的产生，并大幅度改善了车流量、平均速度等交通流参数值。

基于离散选择行为的换道模型通过估计重要属性的影响，使用Logit或Probit分析来模拟驾驶员行为。在这些模型中，驾驶员的决定为二元或多重选择，计算所有可选方案的效用，能够获得每个方案的实施概率，最后根据实际数据标定间距接受模型的参数。Hidas[5]基于视频数据提出的换道模型，可以根据速度、间距接受度和冲突解决三个方面重现单个车辆的换道行为，并且以一种逼真的方式模拟了高度拥堵时的交通流状态。Kesting等[6]考虑驾驶员因素，提出了“礼貌因子”，该参数允许将车道变换的动机从纯粹的自我主义变为更加协同的驾驶行为。Sun等[7]提出了基于驾驶员行为的换道模型，通过考虑各种影响换道的因素得出换道概率模型，可以更好地模拟不同交通流状态下的车辆换道行为。

车间通信技术实现了车辆间的信息交互，为换道策略的研究提供了支撑。Wang等[8]使用博弈论进行换道预测和跟车控制，提出了基于自动驾驶系统的后退视野控制方法，以评估车道变化、决定和控制加速，从而形成最佳的换道决策。Talebpour等[9]基于车间通信环境，应用博弈论模拟换道行为，能够预测车辆的车道变换行为，但存在一定的局限性。2016年，Du等[10]提出了多车道城市道路燃油节能控制策略，基于车间通信系统，考虑信号灯相位、时序和换道决策，以减少车辆的能源消耗。Nie等[11]提出了针对车间通信车辆的换道决策框架及算法，结果表明在动态交通系统中该换道决策框架对交通稳定性及效率表现出很高的潜力。Kamal等[12]基于对周边交通环境的详细预测，提出了一种基于车间通信环境的高效车辆驾驶系统，仿真分析表明该系统可以优化车辆的换道行为，并且提高车辆的燃油经济性和通行效率。Yao等[13]提出了基于车间通信的换道规则，并将其引入优化速度模型，但该换道规则的换道动机是从单个车辆的角度出发的，没有从系统的角度考虑其对交通流的影响。

目前，基于车间通信的智能交通技术仍处在起步阶段，现有研究都是基于模型的理论分析或模拟分析，并且基于单一目标(如提升系统效率等)的研究居多，基于车间通信的换道策略的研究尚不多见。本文以抑制换道产生的干扰和提升道路交通的运行效率为目标，提出基于车间通信的换道策略，并通过数值模拟，研究其对交通流的影响，以期为车间通信技术在实际交通中的应用提供理论依据和科学方法。

1 普通车的换道模型

1.1 换道模型

根据对换道行为的研究，换道分为两个步骤：首先确定换道意愿，然后根据换道规则决定是否换道。

(1)步骤一：换道概率确定

为了细致地描述车辆换道行为，基于对日常换道行为的研究，考虑换道车辆与其当前车道前车、目标车道前后车距离Δxown，Δxother，Δxotherback和车速差Δvown，Δvother，Δvotherback等因素。根据影响换道的相关因素，选择具有二元因变量的Logit模型来估计各种换道环境下的换道概率，因此，构建如下换道概率模型：

(1)

其中，PLC表示换道的概率，VLC表示换道的效用函数，可以表示为：

VLC=β0+β1Δxown(t-τ)+β2Δxother(t-τ)+β3Δxotherback(t-τ)+β4Δvown(t-τ)

+β5Δvother(t-τ)+β6Δvotherback(t-τ)，

(2)

其中，βi(i=0,1,2,…,6)是需要标定的参数，τ为时间延迟。效用函数中换道车辆与前车、侧前车的距离Δxown，Δxother和车速差Δvown，Δvother这四个因素主要影响换道动机的产生，换道车辆与侧后车的距离Δxotherback和车速差Δvotherback这两个因素主要影响换道的安全性。

(2)步骤二：换道规则

由公式(1)和公式(2)确定了车辆换道概率后，由如下换道规则，即公式(3)确定是否执行换道：

(3)

其中，l0和l0,back为换道规则中的特定参数，为了确保安全，规则(1)表示换道车辆与侧前车距离大于特定值，规则(2)表示换道车辆与侧后车的距离大于特定值。因此l0和l0,back取值如下：

(4)

这里，l0取车辆当前速度和最大行驶速度的最小值，l0,back取车辆的最大行驶速度，其目的是为了保证车辆换道的安全。

1.2 换道模型参数标定

本文选用NGSIM轨迹数据，使用US-101高速公路的轨迹数据对模型参数进行标定，其记录了2005年6月15日上午7:50 —8:35共计45 min 的数据，数据中记录了每辆车间隔0.1 s的精确轨迹数据。选取换道数据266组和不换道数据295组，考虑到驾驶员做出换道决策是在换道行为产生前的一段时间，存在时间延迟，因此，本文分别用换道前0.1、1、2、3、4、5、6、8、10、12 s的数据各266组，并结合不换道数据295组对模型参数进行标定。进行二项Logistic回归分析，标定结果见表1～4。

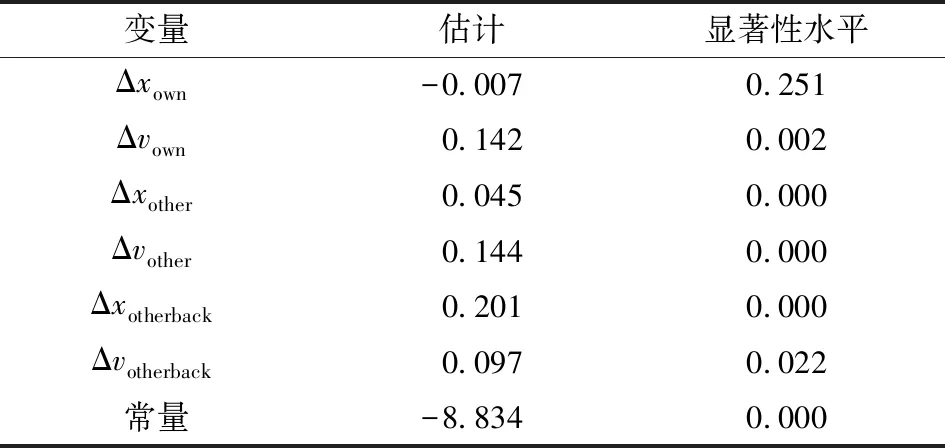
表1 换道前1 s数据标定结果

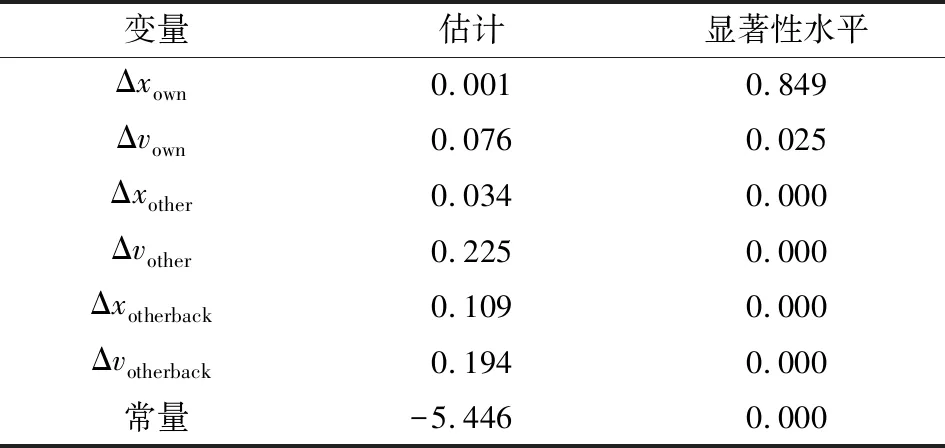
表2 换道前4 s数据标定结果

表3 换道前5 s数据标定结果

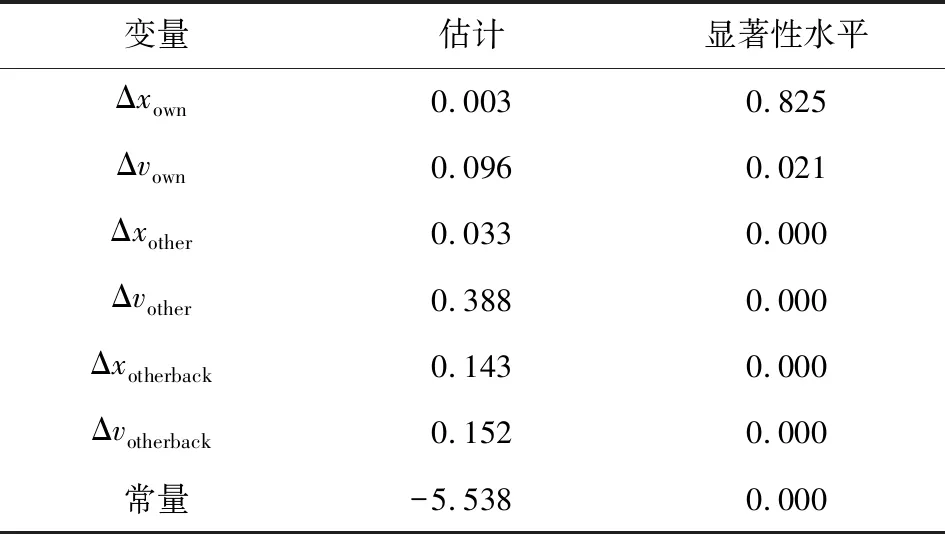
表4 换道前6 s数据标定结果

表5 Hosmer-Lemeshow检验结果

表1～4中，显著性水平p<0.05的变量被剔除，可以看出时间延迟为5 s时所有影响因素均被选入模型，并且从表5显示的Hosmer-Lemeshow检验结果可以看出，时间延迟为5 s时显著性水平最小，且卡方值最大，表明用时间延迟为5 s的数据拟合出的结果是最好的。并且根据张颖达等[14]对基于NGSIM轨迹数据的换道行为的研究，换道时间为2.8～13.8 s。因此，本文选用时间延迟为5 s时的参数标定结果符合一般的统计规律。

基于参数标定的结果，最终确定换道概率模型如下：

(5)

VLC=-4.725+0.007Δxown(t-5)+0.027Δxother(t-5)+0.089Δxotherback(t-5)

+0.073Δvown(t-5)+0.235Δvother(t-5)+0.193Δvotherback(t-5)。

(6)

2 互联车的换道模型

互联车配有先进的传感器和通信设备，换道车辆不仅可以获取其前车、侧前车和侧后车的信息，而且，借助车间通信技术，换道车辆可以获取其周围一定范围内所有车辆的信息，实现车辆间信息的互联互通。为分析得出换道策略，做换道分析图，见图1。

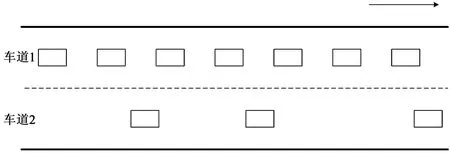
图1 换道分析图1Fig.1 Lane-changing figure I

如图1所示，车道1上的车辆数目远大于车道2上的车辆数目，并且车道1上车辆间的车间距普遍小于车道2上车辆间的车间距，如果车道上的车辆不进行换道，将会大大降低整个道路交通系统的运行效率，故车道一上的部分车辆应该换到车道2，尽量保证两车道上车辆间距相同。基于此，利用车间通信技术获得车道上所有车辆的车间距信息，分别求出两车道上车辆间距的平均值，并比较大小，车辆更倾向于换向车辆间距均值更大的车道上。

为了充分合理地利用车道上所有车辆的车速信息，做换道分析图，见图2。

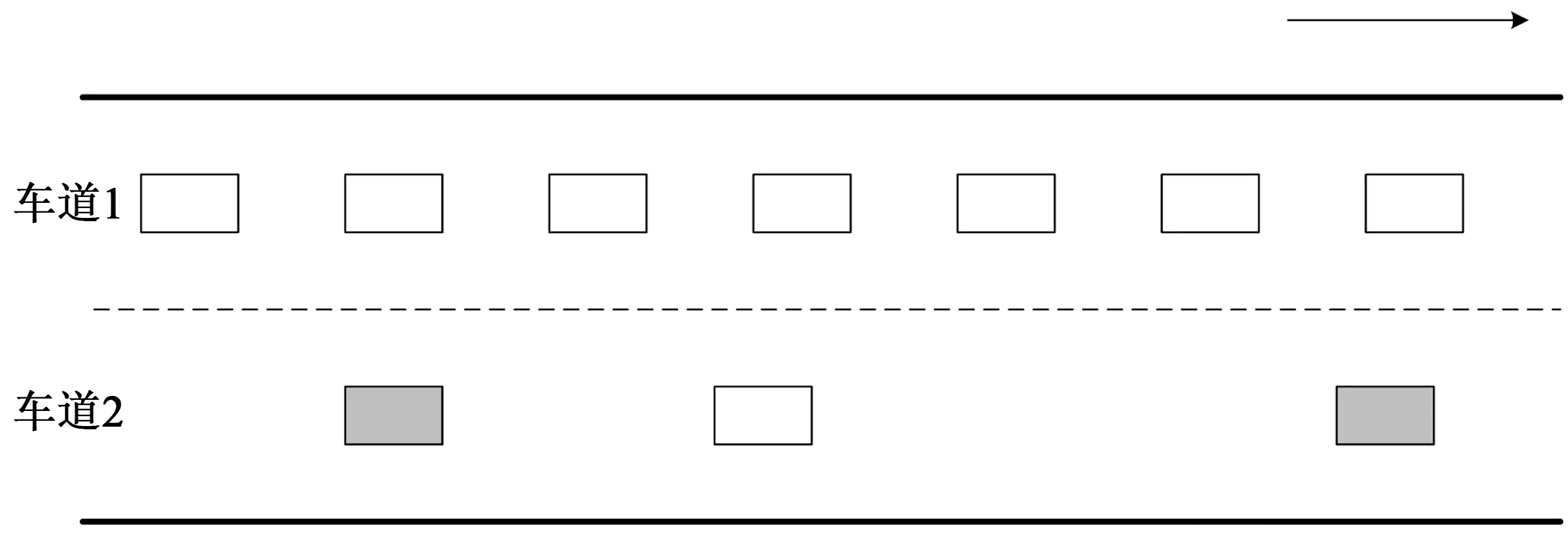
图2 换道分析图2Fig.2 Lane-changing figure II

如图2所示，车道上灰颜色的车辆代表车速较快的车辆，白颜色的车辆代表车速较慢的车辆，由于车道1上的车辆过多，导致车道1处于比较拥堵的状态，车道2上的车辆较少，车辆行驶速度也较快。因此，车道1上的部分车辆应该换到车道2，尽量保证两车道上车辆速度大体相同。基于此，利用车间通信技术获得的车道上所有车辆的车速信息，分别求出两车道上车速的平均值，并比较大小，车辆更倾向于换向车速均值更大的车道上。

因此，可以利用这些信息来设计基于车间通信技术的换道策略。本文设计如下换道模型：

(7)

VLC=θ{-4.725+0.007Δxown(t-5)+0.027Δxother(t-5)+0.089Δxotherback(t-5)

+0.073Δvown(t-5)+0.235Δvother(t-5)+0.193Δvotherback(t-5)}

(8)

公式(8)对换道模型的效用函数做出了改变，θ表示普通车信息所占的百分比，利用互联车信息的部分表示一定范围内目标车道所有车辆车间距的加权平均值和本车道所有车辆车间距的加权平均值之间的差值，以及目标车道所有车辆车速的加权平均值与本道所有车辆车速的加权平均值之间的差值，α1和α2分别表示这两种信息所占权重。前者可以减小换道带来的干扰，后者可以增加换道后车辆的行驶速度。两者共同作用的效果所占权重为1。

(9)

(10)

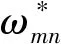
通过公式(7)和公式(8)的换道概率模型计算出换道概率，然后使用公式(3)所示规则确定是否换道。

3 仿真分析

本文的数值模拟采用周期性边界条件。假设车辆在长度为2 km的环形双车道道路上行驶。初始时，车辆在两条车道上随机分布，所有车辆的初始速度与加速度均为0。

3.1 换道模型参数分析

为了研究不同参数对交通流的影响。首先，固定α1=0.5和α2=0.5，道路上分别加载180辆车和240辆车时(分别对应亚稳态和拥堵流的交通流状态)，仿真结果如表6 ～7所示。

根据表6～7，发现互联车信息所占比重越大，即θ值越小，道路上车辆的换道次数越少，说明互联车信息对车辆的换道行为有一定的抑制作用。并且互联车信息所占权重和普通车信息所占权重相似的时候，车辆的平均速度较大，速度的标准差较小，流量较高，即道路上车辆行驶的波动性较小，道路交通系统的通行效率较高。

然后，固定θ=0.5，道路上分别加载180辆车和240辆车时(分别对应亚稳态和拥堵流的交通流状态)，仿真结果如表8～9所示。

根据表8～9，发现互联车平均车速信息所占权重和车间距信息所占权重相似的时候，即α1的值在0.5附近，车辆的平均速度较大，速度的标准差较小，流量较高，即道路上车辆行驶的波动性较小，道路交通系统的通行效率较高。

表6 加载180辆车时的结果

表7 加载240辆车时的结果

表8 加载180辆车时的结果

表9 加载240辆车时的结果

3.2 换道策略对交通流影响的模拟分析

根据表6～9的结果，为了突出显示信息作用对交通流的影响，选择如下换道策略参数进行模拟分析：θ=0.5，α1=0.4和α2=0.6。

我们首先模拟了基于车间通信的换道策略对流量-密度关系的影响，见图3，图中曲线圆点表示所有的车辆都为普通车辆构成，三角形表示所有的车辆都为互联车构成。

从图3可以看出，曲线可以划分为3个部分：自由流部分(0～30 辆/km)、拥挤流部分(60～120 辆/km)和中间部分(30～60 辆/km)。自由流和拥挤流部分，两条曲线基本重合，而中间部分(当车辆密度超过30 辆/km时)，普通换道模型的流量-密度曲线会出现较大的波动，这是由于普通换道模型没有充分考虑换道行为对目标车道上的车辆造成的影响，一些不必要的换道行为会增加本车道和目标车道上车辆的急加速和急减速，从而增加了交通流的波动性，而基于车间通信的换道策略不会出现这种现象，这是由于这种换道策略通过使用车间通信技术，在换道概率模型中利用两条车道上所有车辆车速的均值及车间距的均值，很大程度上减少了换道对目标车道上车辆的干扰，从而提升了道路交通系统的稳定性。当车辆密度达到30 辆/km时，两类模型的流量-密度关系图均达到了最大流量值，可以看出本文设计的换道策略所能达到的最大流量比普通换道模型高，说明基于车间通信的换道策略不仅可以提升交通系统的稳定性，而且可以增加道路交通系统的通行效率。

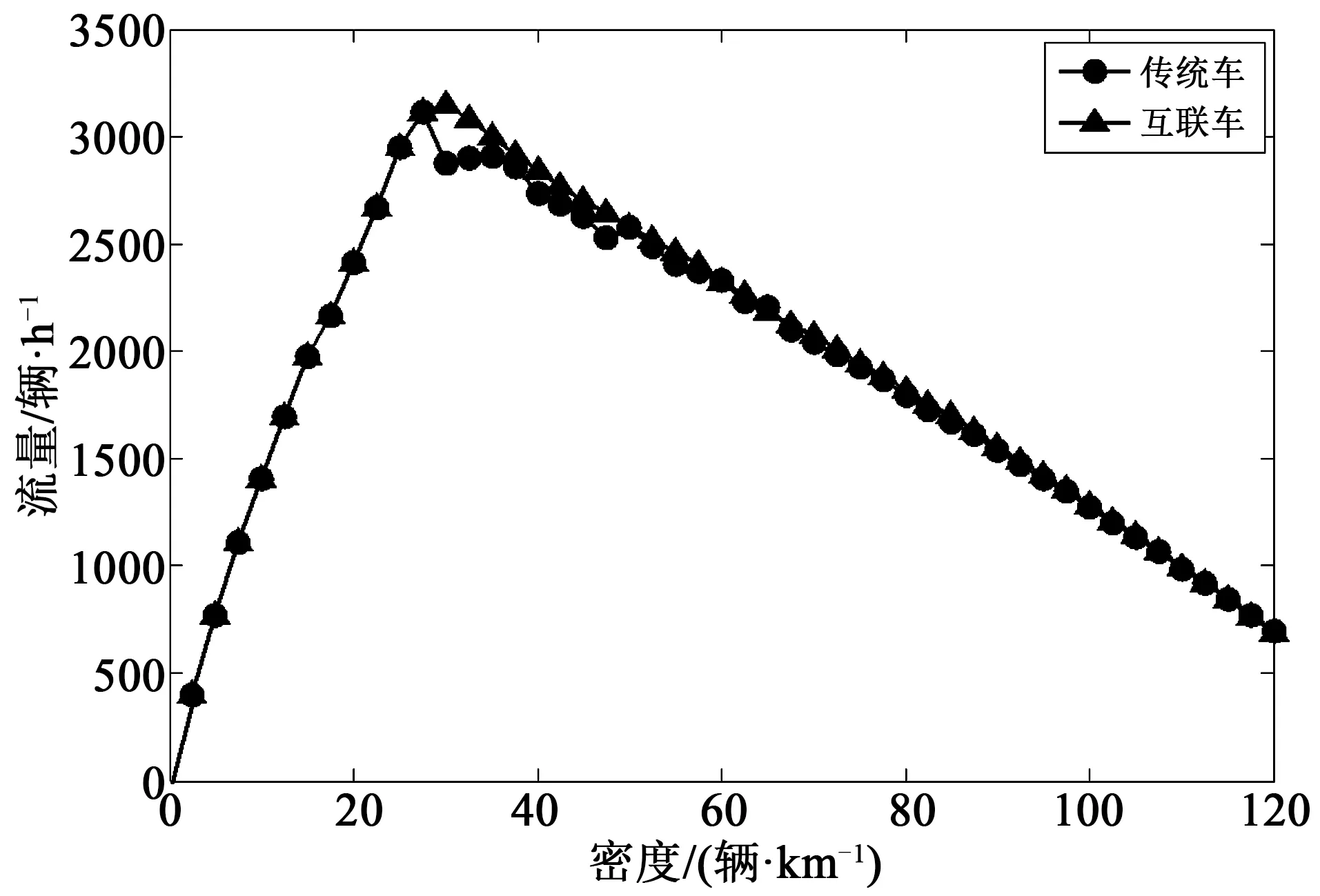
图3 两类换道模型的流量-密度图Fig.3 The flow-density diagram obtained using a two-stage lane-changing model

为了研究两类换道模型对车辆换道次数的影响，仿真分析了不同车辆密度下两类模型的换道次数。

从图4可以看出，随着车辆密度的增加，车辆换道次数在不断减小，当车辆密度在中间部分(30～60 辆/km)，两类模型的换道次数均呈现下降趋势，并且普通车的换道次数明显多于互联车的换道次数，而当车辆密度达到拥挤流部分(60～120 辆/km)，两类模型均产生极少的换道行为，甚至不进行换道。出现上述现象的原因，主要是由于当车辆密度小于60 辆/km时，随着车辆密度的增加，道路的拥挤程度增加，换道行为潜在的安全隐患越来越大，车辆的换道次数自然随之减少。由于基于车间通信的换道策略考虑了一定范围内本道和目标车道所有车辆的速度及位置信息，效用函数使得车辆更倾向于向平均车速快和平均车距大的车道换道，从而大大抑制了换道产生的干扰，并增加了道路交通系统的通行效率，而传统的换道模型由于不具备车间通信技术，不能使用较多的周围车信息，基本只要满足换道动机和安全条件就进行换道，因此，普通车的换道次数明显较多，并且会产生较大的干扰，影响道路交通系统的通行效率，这也进一步印证了图3所示的现象。当车辆密度达到拥挤部分，换道不会增加道路的通行效率，而且存在很大的不安全性，因此两类换道模型均产生极少的换道行为，甚至不进行换道。

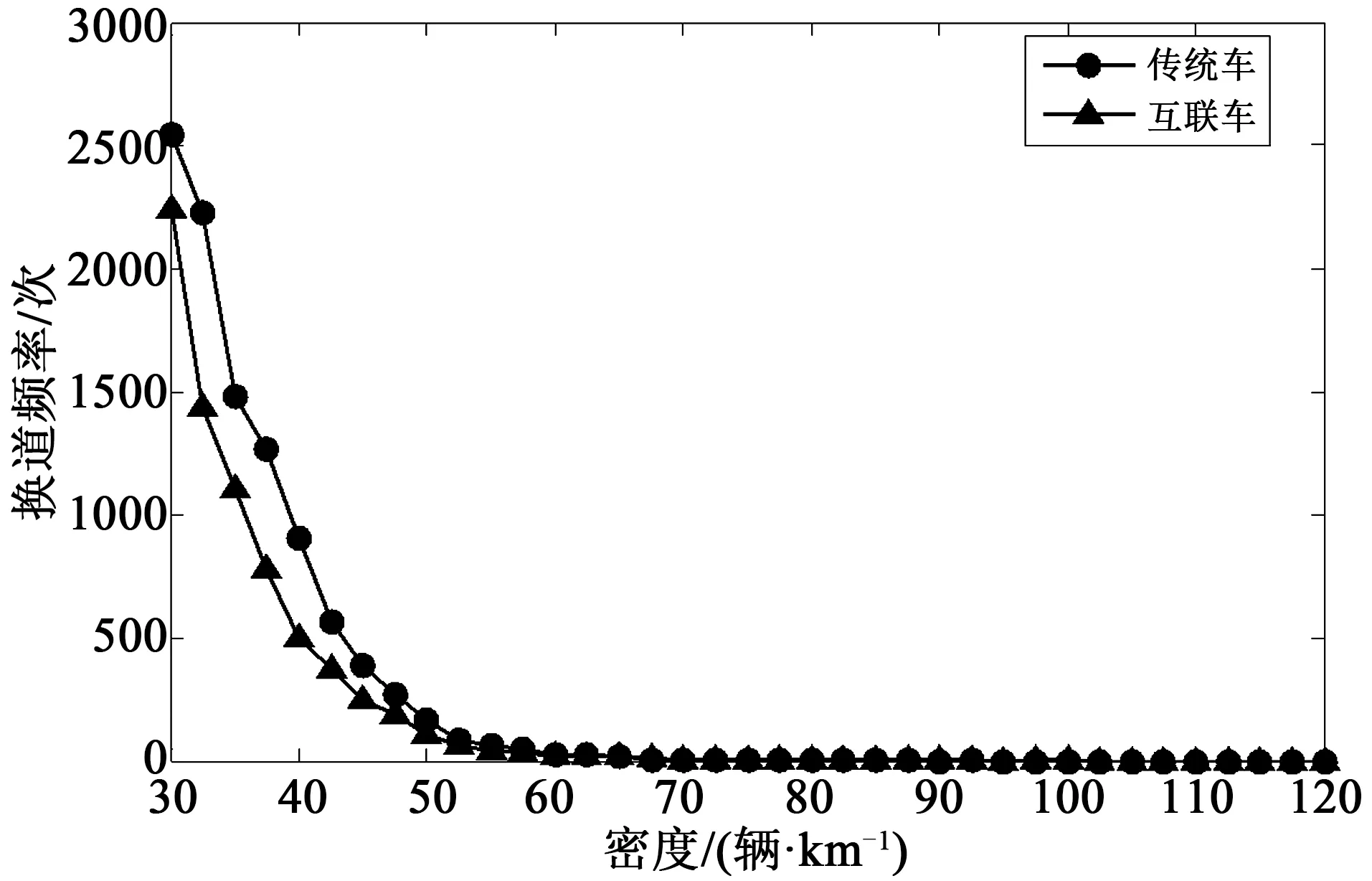
图4 两类换道模型的换道频率对比图 Fig.4 A comparison of the lane-changing frequencies for a two-stage lane-changing model

本文进一步模拟分析了不同交通流状态下，两类换道模型对交通流的不同影响，仿真分析了车辆密度分别为40 。100 辆/km时两类换道模型的车速对比图，见图5。

从图5可以看出，当车辆密度为40 辆/km时，此时交通流状态为亚稳态，互联车的速度曲线能较早地达到稳定状态，并且互联车的速度波动比普通车的速度波动小。基于车间通信的换道策略考虑了一定范围内本道和目标车道所有车辆的速度及位置信息，其效用函数使得车辆更倾向于向平均车速快和平均车距大的车道换道，从而大大抑制了换道产生的干扰，而普通的换道模型不能考虑较多的周围车信息，只要满足换道动机和安全条件就进行换道，因此，互联车的速度波动较小并且其速度曲线可以较早达到稳定。当车辆密度为100辆/km时，交通流状态为拥堵流，为了保证车辆的安全行驶，两类换道模型均不会产生过多的换道行为，因此互联车的速度曲线和普通车的速度曲线十分接近。

图5 两类换道模型的车速对比图Fig.5 A comparison of the speeds in two types of lane-changing models

4 结语

本文主要设计了车间通信技术下车辆换道策略模型，并研究其对道路多驾驶模式交通流状态与效率的影响。首先，构建了两阶段换道模型，其中第一阶段确定驾驶员的换道意愿，即确定换道概率；第二阶段通过换道规则，即安全条件确定车辆是否可以实施换道。进而基于NGSIM轨迹数据对模型参数进行标定。进一步基于车间通信技术对车辆换道策略进行设计，最后通过数值模拟分析提出换道策略对交通流的影响。结果表明，当交通流状态为亚稳态时，基于车间通信的换道模型不仅减少了换道带来的干扰，而且提升了道路交通系统的运行效率。

然而，交通系统是综合人、车、道路与环境的复杂系统，车间通信技术的发展为交通系统引入了更加多样的影响因素。为此，研究基于车间通信技术的建模方法，并通过理论分析与数值模拟深入探讨其对交通系统的影响；同时，考虑换道行为是最基本的交通行为之一，进一步深入研究协同换道策略，并分析其对交通流状态，以及交通安全状态的影响，是今后工作中面临的重要问题。