改进WOA算法优化SVM的网络入侵检测

徐 慧， 付迎春， 付朝川， 叶志伟

(湖北工业大学 计算机学院， 武汉 430068)

0 引 言

随着信息技术的发展，计算机网络已成为人们生活和工作中的一部分。然而，计算机病毒和恶意的网络攻击等使得网络安全面临着巨大的挑战[1]。

支持向量机(Support Vector Machine, SVM)是一种分类模型，它在解决小样本、非线性及高维模式识别中具有许多特有的优势，且可以保持很好的分类准确率，用于网络入侵检测[2-3]。网络入侵检测中常用的检验标准是准确率，而准确率的好坏与SVM的参数具有很大的关系，当SVM参数取值不当时，所得到的分类准确率就会有所影响，甚至极差。关于如何才能得到SVM中的最优参数值，学者们更多地是采用了一些智能算法对其进行优化，比如：粒子群算法、蚁群算法，萤火虫算法与人工蜂群算法等智能算法都可以用于优化SVM的网络入侵检测，且在网络入侵检测的准确率上都有明显的提高[4-10]。

与网络入侵检测的传统检测方法以及常用的检测算法(KNN算法、模糊聚类和贝叶斯算法等)相比，融合智能优化算法的网络入侵检测方法在识别入侵攻击时，具有特殊的处理方式。虽然这些融合智能优化算法的研究在一定程度上都取得了不错的实验效果，但智能优化算法的本身还是存在着一定的局限性。比如：遗传算法的过早收敛问题；蚁群算法的搜索时间长、容易出现停滞现象；粒子群的精度较低、易发散等缺点；鲸鱼优化算法存在着收敛速度慢和容易陷入局部最优的缺点[11-12]。

为了改善鲸鱼优化算法(Whale Optimization Algorithm，WOA)的不足，学者做了一些相关研究。许瑜飞等[13]提出一种基于结合差分进化和精英反向学习的改进的WOA，提高WOA的收敛速度和跳出局部最优能力。牛培峰等[14]提出一种反向学习自适应的WOA，结果证明其具有更好的收敛速度。针对WOA的不足，前期工作已经提出一种改进二进制鲸鱼优化算法(Improved Binary WOA，IBWOA)[15]，该算法采用非线性收敛因子来平衡全局和局部搜索能力，更新机制中融入粒子群优化策略保证种群多样性，来提高它的收敛速度和降低陷入局部最优的概率。

为了改善因SVM参数值设置不当导致网络入侵检测的分类性能下降的问题，本文在先前工作的基础上提出改进二进制鲸鱼算法优化SVM(IBWOA-SVM)的网络入侵检测。IBWOA-SVM方法通过对WOA算法中的收敛因子和更新机制的改进，来弥补WOA算法容易陷入局部最优和收敛精度慢的不足。针对SVM参数的寻优问题，IBWOA-SVM方法通过对随机生成的参数群不断的更新迭代，并由评价函数的评判标准找到SVM的最优参数来建立最优的分类器，以达到提高网络入侵检测分类准确率的目的。

1 相关理论知识

1.1 SVM

SVM是Cortes等提出的一种分类模型，它是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的。SVM的分类思想是尽最大努力使分开的两个类别有最大间隔，这样对于未知的新样本才能达到很好的分类预测能力。

为了将样本进行有效地分类，SVM需要寻找一个线性函数——超平面。对于给定的训练集样本(xi,yi),i=1,2,…,n,x∈Rd,yi∈{-1,1}，它分类的超平面为：

y=ωT·x+b

(1)

式中：ω为分类超平面的系数向量；b为偏移向量。

为了发现目标函数的全局最小值，可以将式(1)转化为一个凸二次规划优化问题：

式中：ξi为松弛向量；C为惩罚参数。引入Lagrange乘子将式(2)转化为对偶问题

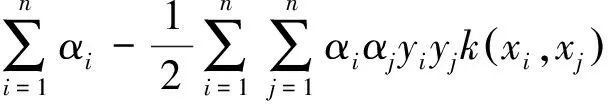
(4)

(5)

式中：k(xi,xj)为核函数；αi为Lagrange乘子。基于上述公式可得到相应的分类模型：

(6)

式中：sgn()函数用来判断样本的类别。由于不同的核函数将建立不同的SVM分类模型，本文采用RBF函数作为SVM核函数，其公式如下：

(7)

式中，g为核参数。

1.2 鲸鱼优化算法

WOA在狩猎过程中包含了：环绕包围猎物、随机搜索狩猎、螺旋轨迹狩猎。其中，用参数A来判断座头鲸的狩猎行为是环绕包围猎物还是随机搜索猎物。

(1) 环绕包围猎物。当|A|<1时，在鲸鱼种群中，选择最好的鲸鱼个体X*作为猎物，其余的鲸鱼个体会向这个位置逐步靠近包围猎物。其位置更新公式如下：

D=|C·X*(t)-X(t)|

(8)

X(t+1)=X*(t)-A·D

(9)

式中：t表示当前迭代次数；X为当前鲸鱼个体的位置;A和C为系数矢量:

A=2a·r-a

(10)

C=2r

(11)

r为[0,1]内的随机数；a表示从2～0呈线性变化的值：

(12)

max_t为最大迭代数。

(2) 随机搜索狩猎。当|A|≥1时，在当前的种群中随机选择一个鲸鱼个体Xrand作为种群最优解来更新其它鲸鱼个体的的位置：

(3) 螺旋轨迹狩猎。当鲸鱼在寻找猎物时，会针对猎物的位置通过一个螺旋形方程式作为运动轨迹来捕获食物，其更新公式如下：

式中：b为常数；l为[-1,1]之间的随机数。

2 基于改进二进制WOA的SVM参数优化

2.1 改进的二进制WOA

为了改善WOA算法在搜索过程中的收敛速度慢和陷入局部最优的缺点，提出一种改进二进制鲸鱼优化算法(IBWOA)。

(1) 非线性收敛因子策略。为了更好地协调算法的全局搜索和局部搜索，本文提出一种新的非线性收敛因子策略，

(17)

(2) 更新机制中引入粒子群优化策略。在WOA算法的更新机制中，为了降低WOA算法陷入局部最优解的概率，本文采用粒子群优化策略对种群进行多样性操作。通过粒子群中的ω权重使算法快速跳出局部极值，使得种群更具有多样性。

v(t+1)=ω·v(t)+r1c1(X*(t)-X(t))+

r2c2(Xg(t)-X(t))

(18)

X(t+1)=X(t)+v(t+1)

(19)

式中：Xg为个体最优位置；ω是速度惯性权重；c1,c2表示学习因子；v(t+1)是t+1次迭代时第i个粒子的速度。

为了实现鲸鱼个体位置在0和1之间的更新转换，本文采用的二进制更新转换函数[9]如下：

(20)

(21)

式中：Xij表示第i个鲸鱼个体第j维的特征；rand()为[0,1]内的随机数。

2.2 IBWOA-SVM方法

SVM的分类性能关键在于参数的设置，只有选择合适的SVM参数，才能得到高维空间的最优分类模型。关于对SVM参数的选取，目前研究最热的是采用智能优化算法来优化SVM参数方法，比如：粒子群、蚁群和人工蜂群等。但是，这些智能算法存在着收敛速度慢以及容易陷入局部最优等不足。因此，本文在前期工作的基础上，提出一种IBWOA-SVM方法，用来优化SVM的两个重要参数(惩罚参数C和核参数g)，进而提高分类的准确率。

2.2.1 流程图

图1所示为IBWOA-SVM方法的流程图。

图1 IBWOA-SVM方法的流程图

IBWOA-SVM方法的具体优化步骤如下:

(1) 数据预处理，设置种群数量n、最大迭代次数max_t、设定C和g的取值范围。

(2) 将SVM的参数设定为每个鲸鱼个体，初始化种群。

(3) 由K折交叉验证法计算每个鲸鱼个体的适应度值，记录当前个体及种群最优值。

(4) 采用改进后的IBWOA算法对种群个体进行位置更新。

(5) 再次计算适应度值，通过适应度值的比较，更新个体最优解及种群最优解，并获取新的种群。

(6) 判断算法是否满足终止条件；若满足，则转到(7)；否则，转到(4)。

(7) 获取最优参数(C,g)。

(8) 采用最优参数对训练样本进行训练建模。

(9) 采用建好的模型对测试样本进行检测。

(10) 输出最优参数(C,g)及分类准确率。

2.2.2 伪代码

算法1IBWOA-SVM。

输入： 最大迭代次数max_t，种群数n，C和g的取值区间。

输出： 最优参数及分类准确率。

1. 初始化种群。

2. 计算个体的适应度值，得到个体最优及种群最优。

3. WHILE 是否满足终止条件。

4. 更新a,l,A,C, 其中a为改进的非线性收敛因子。

5. FOR。

6. WOA算法更新当前种群。

7. 采用粒子群优化策略更新当前种群。

8. END FOR。

9. 再次计算个体的适应度值，更新个体最优及种群最优。

10. 采用最优参数(C,g)对训练样本进行训练建模。

11. 采用建好的模型对测试样本进行检测。

12. END WHILE。

返回最优参数(C,g)及分类准确率。

如算法1的伪代码所示，在IBWOA-SVM的搜索过程中，对参数a采用非线性收敛因子策略，来协调算法的全局搜索和局部搜索；在更新机制中引入粒子群优化策略，来保证种群的多样性，进而提高网络入侵的分类性能。

3 实验分析

3.1 实验设置与环境

为了验证IBWOA-SVM优化方法的有效性，本文分别采用GA-SVM、PSO-SVM、WOA-SVM和IBWOA-SVM方法在多个数据集(机器学习数据库UCI)上的对比实验。

实验采用MATLAB R2014a编程；种群数量n=20，迭代次数max_t=50，K折交叉验证倍数为10，实验次数为50。GA的交叉因子为0.8，变异因子为0.05；PSO的学习因子设置为1.5，惯性权重为[0.3,0.9]。

本文的评价函数如下：

(22)

式中:accuracy分类准确率；cn是正确分类样本数；sn是数据集样本总数。

3.2 UCI数据集实验对比分析

为了验证该优化方法的分类性能，本文采用GA-SVM、PSO-SVM、WOA-SVM和IBWOA-SVM方法在表1所示的4种UCI数据集上各自运行50次进行测试实验，实验将每个数据集的70%作为训练集，30%作为测试集。

表1 UCI数据集

图2所示为各算法在UCI数据集上适应度值的进化曲线。由图2可见，在各数据集上，IBWOA-SVM算法的最好适应度值与其他3种算法相比都有所提高。在4种数据集上，IBWOA-SVM的最好适应度值比GA-SVM、PSO-SVM均提高了2%以上；与WOA-SVM相比，虽然IBWOA-SVM算法的最好适应度值提高的幅度不是很大，但它在迭代过程中的变化较快，可以很大程度地跳出局部最优的可能性，确保得到的解是最优解。

表2是各算法在UCI数据集上的分类准确率以及SVM最优参数值。基于表2和图2的实验结果可知，IBWOA-SVM优化方法在UCI数据集上分类准确率的有效性。因此，进一步将IBWOA-SVM优化方法应用到网络入侵检测中来验证它的可行性。

3.3 KDD CUP 99数据集实验对比分析

KDD CUP 99数据集[16]是网络入侵检测中的常用数据集。本文实验的数据集样本为3 196条，其中每条数据包含41维特征向量和1维类标签。该标签可分为5类，包括：DOS、U2R、R2L、PROBE和NORMAL。由于每条数据都含有字符型特征，所以需要将数据集进行预处理[17]。

表3所示为各算法在KDD CUP 99数据集上的分类结果。图3所示为各算法在KDD CUP 99数据集上适应度值的进化曲线。图中:x轴为迭代次数;y轴为适应度值(最好适应度值和平均适应度值)，以及SVM的最优参数值(C,g)和最好分类准确率。

由图3可知，GA-SVM、PSO-SVM和WOA-SVM方法的适应度值在迭代过程中无明显变化，说明此时种群可能陷入局部最优，找到的解可能为局部最优解。

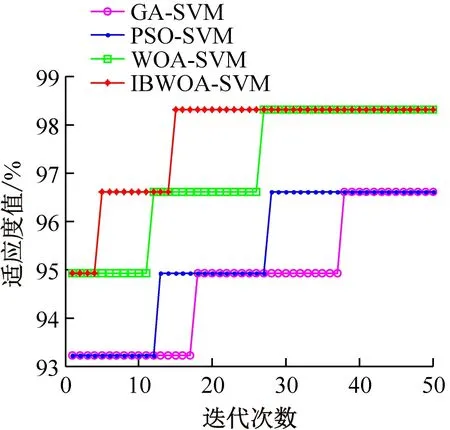
(a) Wine

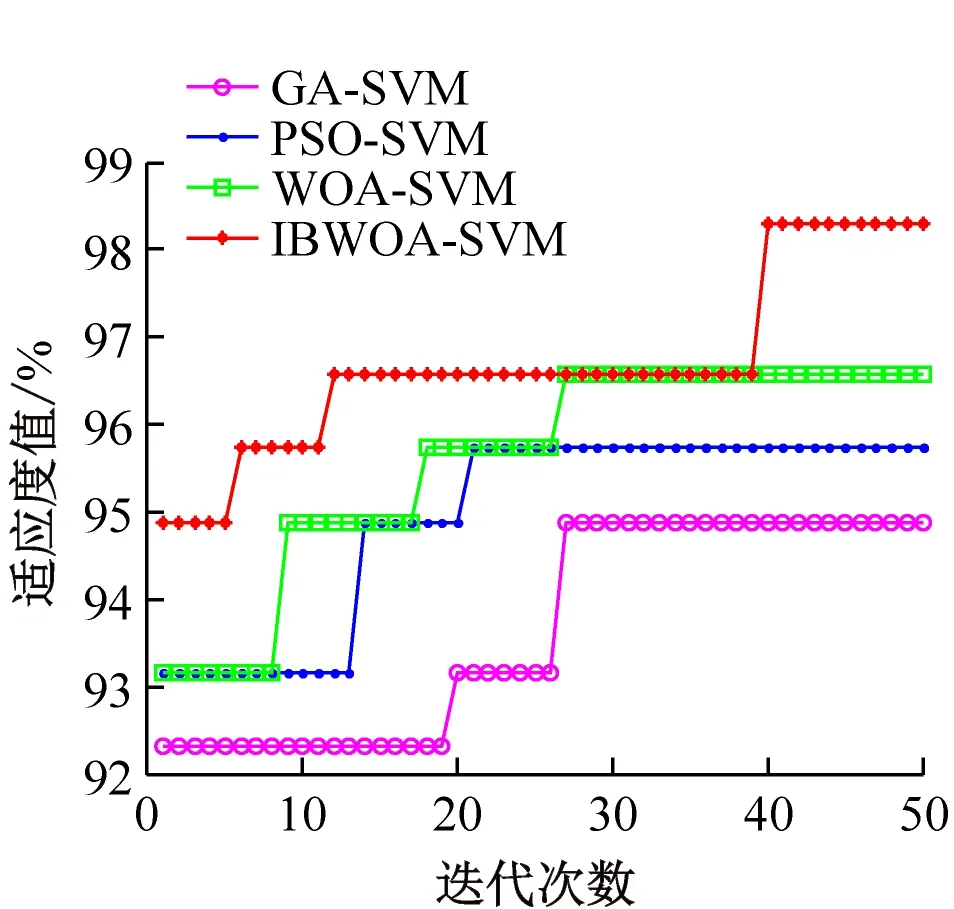
(b) Ionosphere

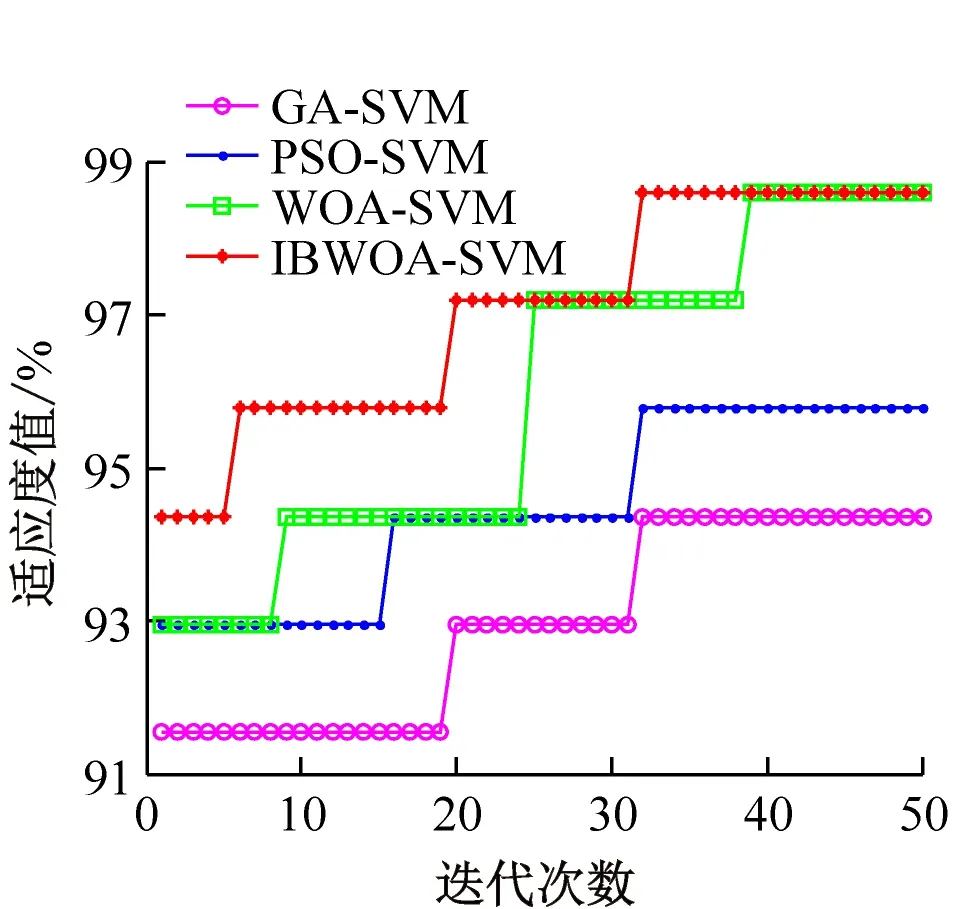
(c) Glass Identification

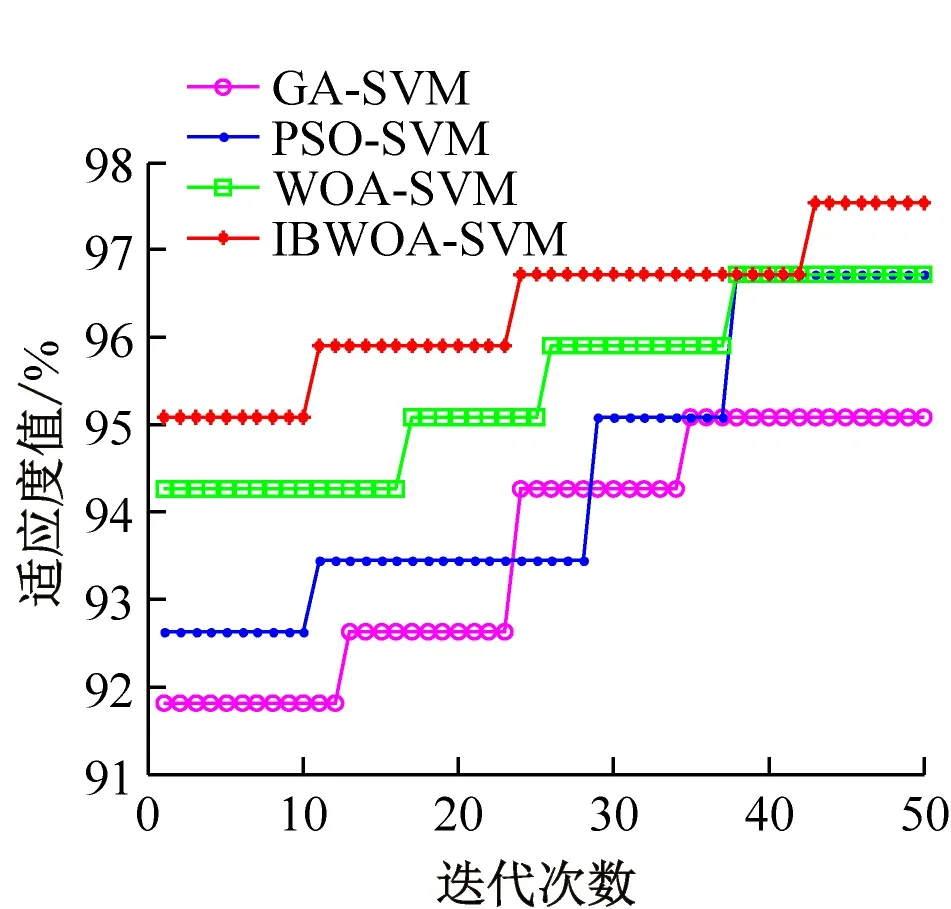
(d) Breast Cancer Wisconsin

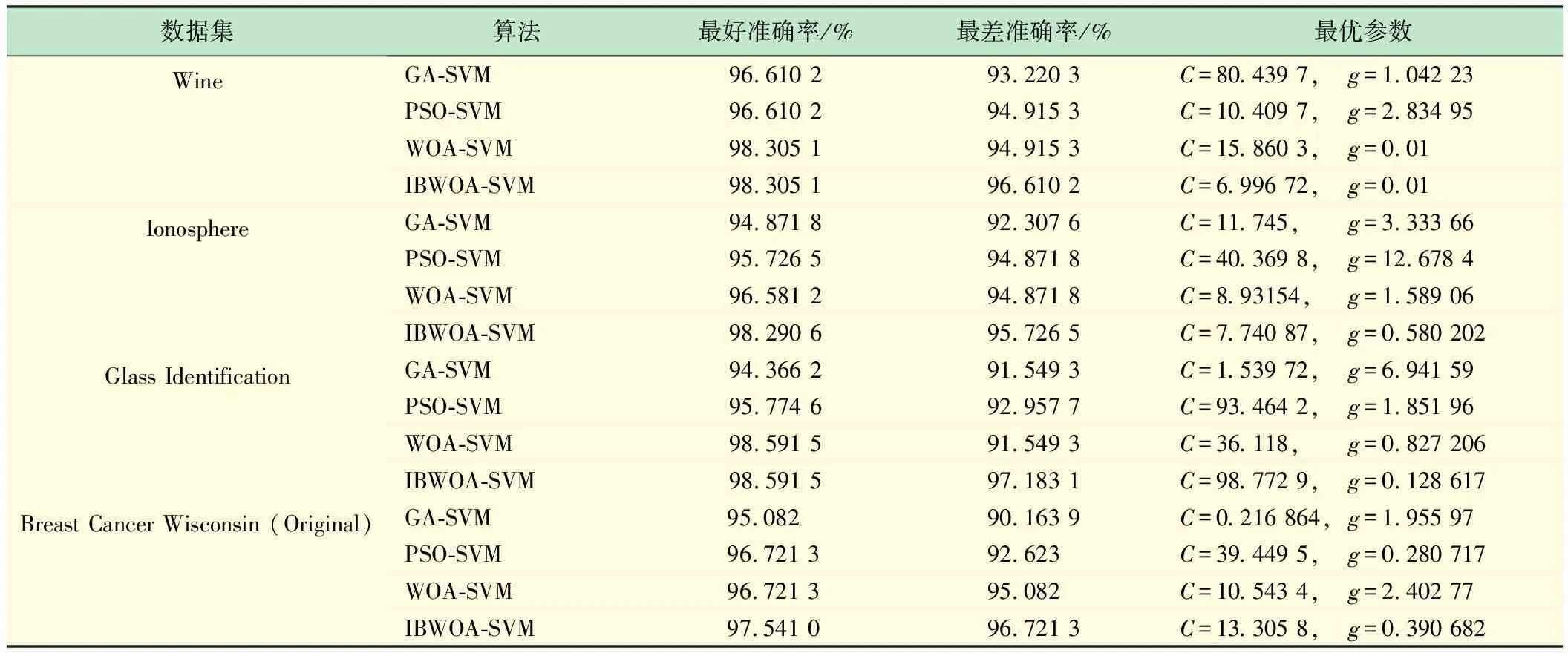
图2 各算法在UCI数据集上适应度值的进化曲线

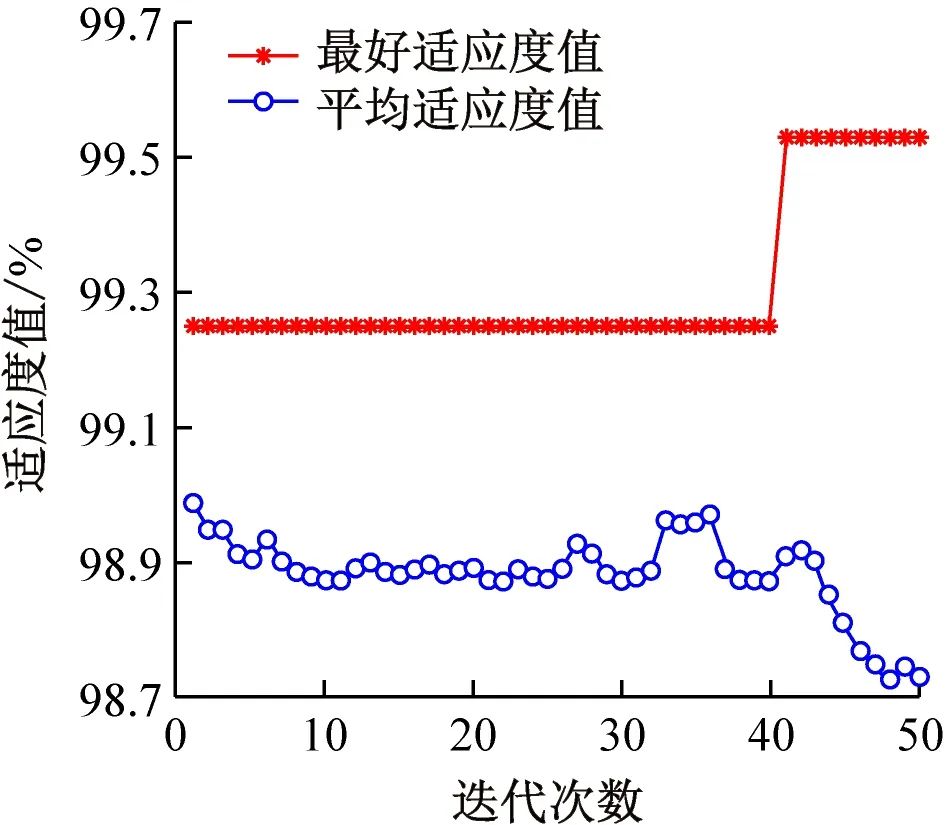
(a) GA-SVM

(c) WOA-SVM

(d) IBWOA-SVM

图3 各算法在KDD CUP 99数据集上适应度值的进化曲线

IBWOA-SVM方法的最优个体在前、中、后期适应度值都有所波动[见图3(d)]，说明IBWOA-SVM方法在寻优过程中避免陷入局部最优的困境，且IBWOA-SVM(99.906 1%)最好适应度值比GA-SVM(99.342 7%)、PSO-SVM(99.342 7%)和WOA-SVM(99.718 3%)的最好适应度值都高。

综上所述，IBWOA-SVM优化方法在迭代过程中适应度值的进化效果较为明显，它很好地避免了陷入局部最优的可能且在优化SVM的参数上分类准确率的效果较优，证明了IBWOA-SVM优化方法在KDD CUP 99数据集上参数优化的有效性。

4 结 语

本文提出基于IBWOA-SVM方法的网络入侵检测。IBWOA-SVM方法采用非线性收敛因子和更新机制中融入粒子群优化策略，来改善在SVM参数优化中WOA算法的搜索能力以及种群的多样性，得到较优的SVM参数来建立分类模型，进而提高SVM的分类性能。

实验将IBWOA-SVM方法在多种数据集上进行验证，并与GA-SVM、PSO-SVM和WOA-SVM方法进行比较，最后在KDD CUP 99数据集上验证其在网络入侵检测中的可行性。实验结果表明，将IBWOA-SVM方法应用于优化SVM网络入侵检测时，在分类准确率和适应度值方面都有所提高，取得了较好的效果。