遗传编程的机构运动链进化设计

华尔天 周 猛 李生辉 鹿 浩

1.浙江工业大学机械工程学院，杭州，3100232.浙江水利水电学院，杭州，310018

0 引言

智能设计正处于由常规设计、联想设计向进化设计突破的关键阶段，传统机构创新设计方法已经不能满足智能设计的发展要求。进化设计是由进化思想指导的设计方法，优良样本的交叉、变异是设计创新的源泉，其优势在于对环境知识依赖较少，在创新求解问题上有很大的发展空间。已有很多进化设计方法应用在各个设计领域和设计阶段。冯毅雄等[1-2]提出零件结构进化模型重构的联动式进化算法，实现对零件结构进化模型的动态编辑；将基于语义单元的创新进化设计理论应用于实际产品开发中，取得良好的效果。章安良等[3-6]将进化设计应用到声表面波技术领域中，针对声表面波滤波器、抽指加权叉指和电容加权叉指换能器等设计过程进行改进，均取得了良好的效果。随着国内外学者对进化设计的深入研究，针对不同的应用领域，对进化设计做出相应的改进。针对进化设计方法在设计理论上的不足，李洪杰等[7]提出基于功能构造的基因模型的框架结构，实现产品的自底向上的适应性设计方式；任尊茂等[8]提出基于单层进化的产品客户化设计方法，通过适应度函数的评价，使进化后的设计方案满足客户的定制需求；针对当前基于几何约束关系的CAD系统不能很好地解决面向方案设计的机构运动模型表示问题，程锦等[9]提出一种新的基于功能语义的运动进化建模方法，为机构运动进化设计过程的自动求解提供有效手段；王吉华等[10]为提高零件进化设计的效率，提出一种基于特征几何体应用程序接口函数的零件基因组模型，并取得良好的效果；针对进化设计中生成解的不可预测性，赵婷婷等[11]提出一种改进的遗传算法——蔓延遗传算法，通过适应度选择生成解并且自动对形状进行可视化。

综上所述，进化设计在许多设计领域已有良好发展。但在机构创新设计领域，却还没有相对完善的进化设计方法。本文将进化算法与传统机构创新设计方法相结合，提出了一种基于遗传编程的机构运动链进化设计方法。

1 机构运动链进化设计的理论基础

1.1 再生运动链法

传统机构创新设计方法中，基于类型综合创新法是根据现有机构，归纳其基本的拓扑特性，通过类型综合方法得到满足基本拓扑特性的所有运动链链型，最后确定可行的链型并进行合理变换，得到满足设计要求的新机构。颜鸿森[12]对该方法进行深入研究后，提出了一种新的创新设计方法——再生运动链法。该方法是在类型综合创新法的基础上，提出的一种更加完备、系统的机构方案创新设计方法，具体实现过程如图1所示。

图1 再生运动链法设计流程图Fig.1 Design flow chart of regenerative motion chain method

近年来，诸多学者运用再生运动链法解决了许多机构设计问题。宋萌萌等[13]在分析玥玛锁具机构的基础上，应用再生运动链法对锁芯机构进行设计，得到新的锁芯机构方案简图；王强等[14]应用再生运动链法对现有的一种内螺纹加工装置进行机构创新设计，将可行解进行机构拓扑特性分析与比较，筛选符合要求的可行运动链。机构再生运动链法逐渐成为机构创新设计的一种指导方法。但该方法也存在着自身局限性，数综合方法[15]设计的新机构与原机构必须具有相同构件数和运动副数，无法得出能够实现相同功能的不同构件数和运动副数组合，限制了可行解的范围，导致具有不同构件数和运动副数的可行解被遗漏，不能保证新机构为满足设计要求的最优解；同时，当构件和运动副数量较大时，运用数综合方法得出的杆件组合较多，但满足设计要求的解仅有一小部分，工作量较大、效率低。

1.2 遗传编程

进化设计的核心是进化算法。遗传编程[16]是进化算法的一个分支，1992年由Koza提出并进行深入的研究。遗传编程的基本思想是：随机产生可行解的初始种群，构成该种群的个体都有一定的适应度，依据适者生存的原则对高适应度值个体进行遗传操作，产生新可行解形成下一代种群；循环该过程即可在某一代出现最优解。具体过程如图2所示。

图2 遗传编程流程图Fig.2 Flow chart of genetic programming

遗传编程与一般遗传算法的主要区别在于：遗传编程的解为树状结构，而遗传算法的解为固定长度的字符串。两者相比，前者具有若干优势，包括：不需要预先给定问题解的结构形式、不定长的树状结构编码可以灵活表示各类问题对象、编码结构可以携带语义信息等。因此，遗传编程能够完成层次化问题的描述，不必像其他进化算法必须通过编码预先定义解空间，适合处理开放解的创新设计问题。

2 设计模型的建立

2.1 机构运动链进化设计流程图

在智能设计的大环境下，现阶段设计方法按照设计能力大致可分为三类：常规设计、联想设计和进化设计[17]。本文提出机构运动链进化设计方法的导图见图3。

图3 机构运动链进化设计导图Fig.3 Evolutionary design map of mechanism kinematics chain

基于遗传编程的机构运动链进化设计，首先将原机构一般化得到一般化运动链，接着将一般化运动链用遗传编程个体树表达，然后通过遗传编程替代数综合方法生成满足设计要求的最优解，最后将最优解进行具体化操作，流程如图4所示。

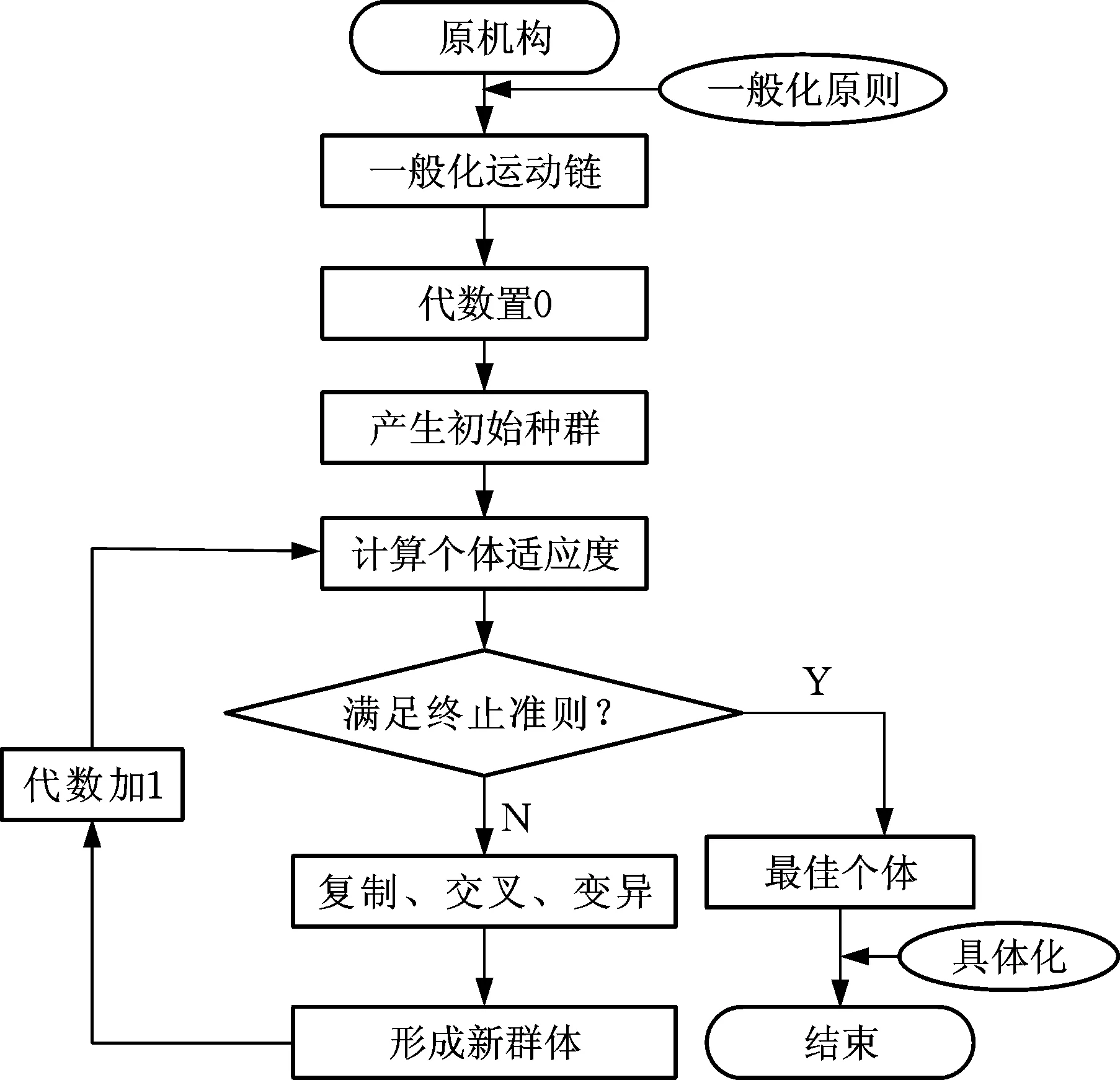
图4 机构运动链进化设计流程图Fig.4 Flow chart of mechanism kinematics chain evolutionary design

运用上述设计流程解决问题时，需要注意：①编码解码方式；②初始群体的生成；③适应度函数的设计；④选择策略与遗传操作；⑤终止准则与相关控制参数的设定。

2.2 机构运动链进化设计数学模型

根据图4所示的设计流程对目标机构进行运动链进化设计，需要根据设计要求与约束，在一般化链中分配特定类型的构件和连接。通过分析设计要求和约束，能够确定可行解的类型，对初始种群的生成设定规则，提高创新设计的效率。机构运动链的设计要求与约束主要包括杆件数和运动副数，以及杆件间的附随关系。本文结合机构设计理论对杆件数和运动副数的约束进行分析，将该约束通过数学方程组的方式表达；同时，结合图论对模型表达方式以及机构创新设计中对图论的应用经验，使用邻接矩阵来表达杆件间的附随关系。

对于一个合理机构来说，除去机架外，必然包括一个或多个必备构件和非必备构件，其中必备构件必须存在，而非必备构件可以被其他相似类型的构件取代。结合设计要求与约束，分析运动链中的必备构件个数，确定必备构件的运动副数，保证通过该进化设计得到的新机构满足原机构的功能特性，并通过数学式表达。

结合图论的知识，将一般化运动链转化为拓扑图，以顶点表示机构运动链的构件，以边表示机构运动链的运动副，并定义如下邻接矩阵A：该矩阵A的行和列均由V(G)进行索引，当i≠j时，若顶点vi和vj不相邻，则A的元素(i，j)取值为0；反之，若顶点vi和vj相邻，则A的元素(i，j)取值为1。当i=j时，即A的对角线上元素(i，i)均为构件(顶点)vi的运动副数。

例如：1个单自由度6杆7副运动链，其中包含必备构件5个，必备构件中要求有2个为三副杆或三副以上的构件，且必备构件1和必备构件2相关联，必备构件3和必备构件4相关联，必备构件1与必备构件5必定不关联。设nt为构件总数，n1为二副杆数，n2为三副杆数，n3为四副杆数，pt为总运动副数，F为自由度数，综合所给约束可得：

(1)

(2)

式中，a为必备构件数，a=5；b为原运动链构件总数，b=6；c为设计要求中必备构件的最小多副杆总数，c=2；F取值为1；nt、n1、n2、n3、pt均为非负整数；xij均为非负整数，x12=x34=1，x15=0。

3 机构运动链进化设计

3.1 编码解码方式

编码是信息从一种形式转换为另一种形式的过程，解码是编码的逆过程。在对机构构件进行编码时，使用编号对应各类杆件，以便计算机录入数据。同时，还需要考虑各类杆件的运动副数，因此采用结构体变量根据构件的运动副数定义各类杆件，构件结构体中包含运动副数量信息，具体如表1所示。

表1 杆件编码信息

Tab.1 Member coding information

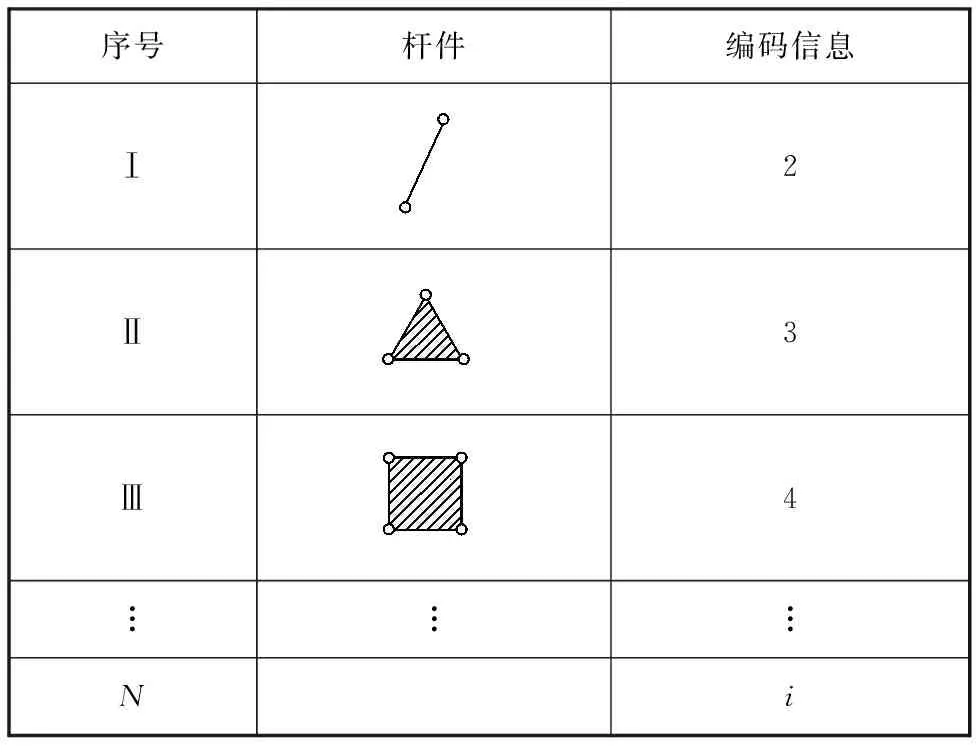
序号杆件编码信息Ⅰ2Ⅱ3Ⅲ4︙︙︙Ni

3.2 一般化过程

再生运动链法中一般化是将含有不同类型构件与运动副的原机构，转化为只含连杆和转动副的一般化运动链。机构的一般化需要遵循一般化原则，一般化原则包括：①非刚性构件一般化为刚性构件；②非连杆形状的构件一般化为连杆；③高副一般化为低副；④非转动副一般化为转动副；⑤解除固定杆的约束；⑥原机构与其所对应的一般化机构，其自由度数应保持不变。

现以飞机鼻轮起落架收放机构为例，对一般化过程和初始化种群进行说明，其机构简图见图5。该机构是一个8杆10副单自由度平面机构，其中连接g为移动副，p、q为复合铰链。

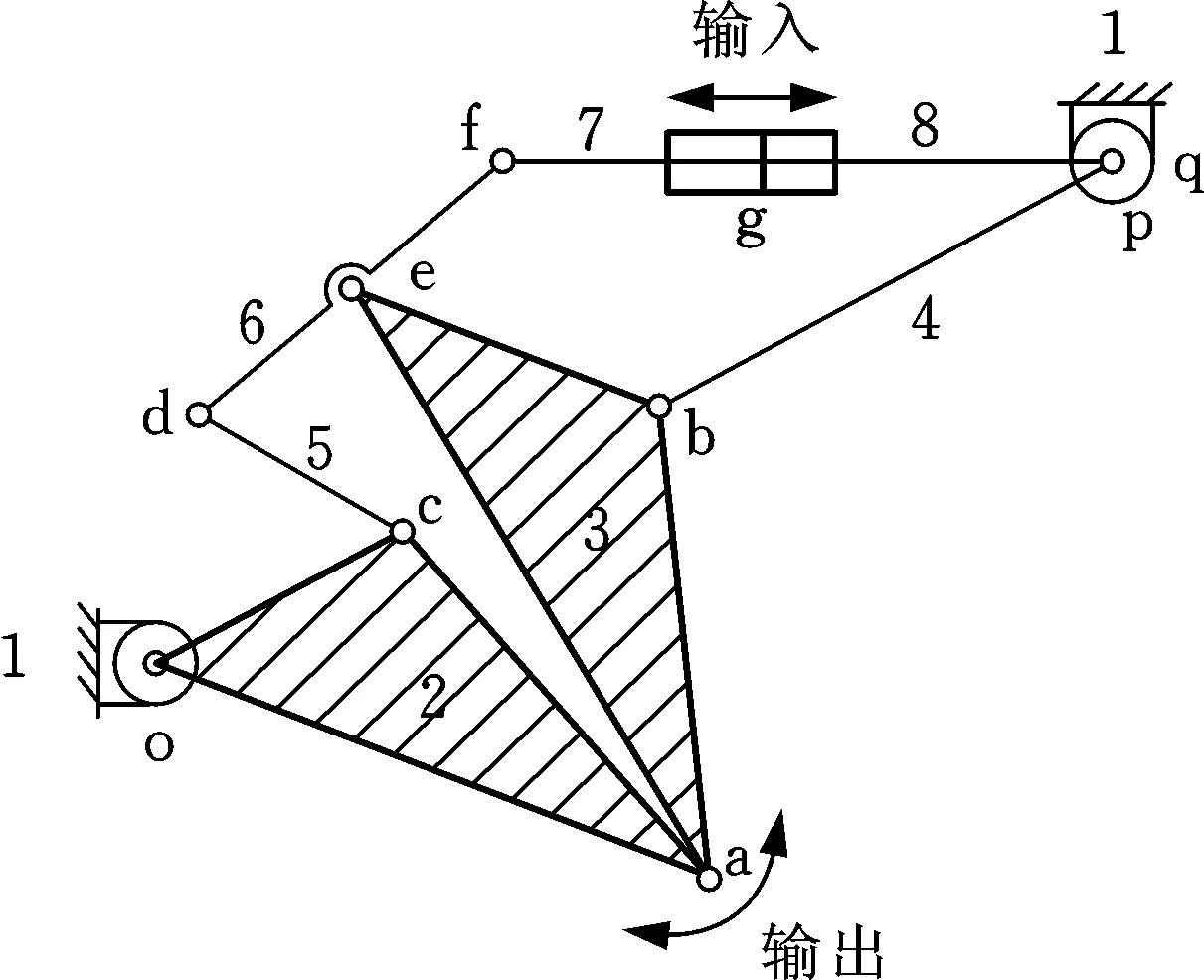
图5 飞机鼻轮起落架收放机构简图Fig.5 Schematic diagram of aircraft nose wheel landing gear operating mechanism

根据一般化原则，对该机构进行一般化。具体过程如下：①将机架(构件1)一般化为三副杆1；②将连接g一般化为转动副。经过转化后得到图6所示的一般化链。

图6 一般化运动链Fig.6 Generalized kinematic chain

3.3 初始化种群

初始群体由众多初始个体组成，初始个体为所要解决问题的各种可能个体树，它通过随机方法产生。针对图6中的一般化运动链，通过整理各零件的运动副数得到对应该一般化运动链的各构件属性表，如表2所示。

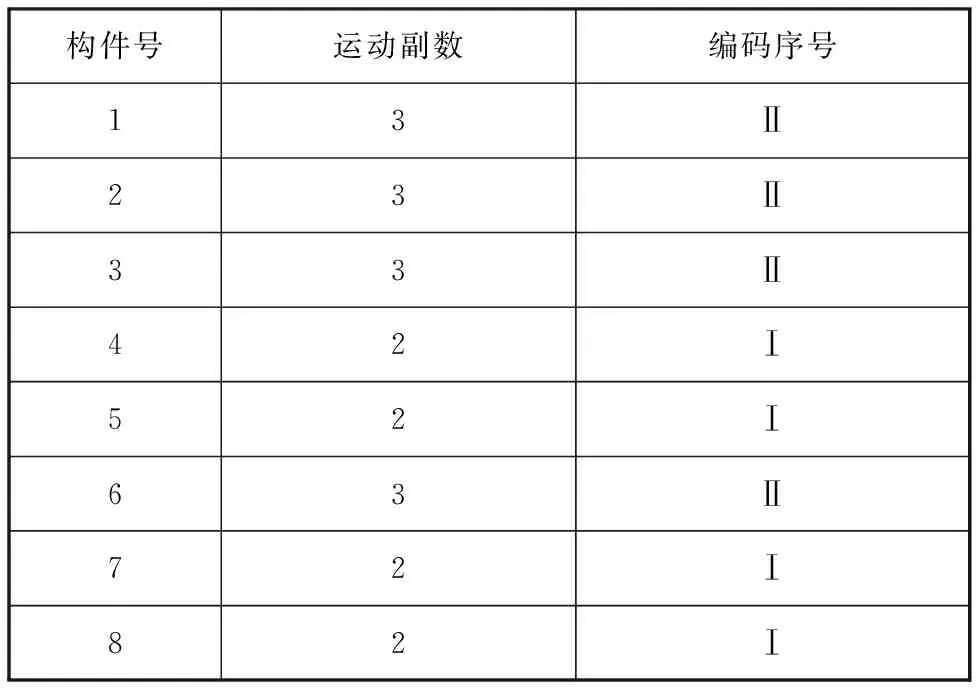
表2 各构件属性表

为方便遗传编程个体的表达，选择某个确定的必备构件作为个体的根，通过该方法可将图6所示的一般化运动链表示为树状结构。其中构件2为必备构件，用于连接机架1与固定鼻轮，选取构件2为个体的根。采用层序遍历的方式来表达个体树，最终得到如图7所示的树。

图7 遗传编程树状解Fig.7 Tree solution of genetic programming

分析该飞机鼻轮起落架收放机构的设计要求和约束，总结出该机构的必备构件数量以及必备多副杆数量，以确定可行解的构件数量和多副杆个数可变动范围，将满足式(1)中各条件的可行解按照事先参数设定的群体数生成相应数量的个体，即完成了遗传编程的初始化过程。

3.4 适应度评价函数

遗传编程适应度评价函数的好坏，直接影响遗传编程所得最佳个体的优劣。根据实际生产需求可选择不同的评价因子，本文主要以构件总数和多副杆数作为衡量指标来建立适应度函数。

公理设计包括独立、信息两大公理[18]，其中，信息公理指出：在所有满足独立性公理的设计中，信息含量最少的设计是最好的设计。因此，设计得到的机构应在满足设计要求的前提下尽可能减少构件总数，使得机构整体信息量最小化；同时，多副杆相对于二副杆而言，其包含的信息量较大。本文根据信息公理的要求，期望得到具有较小构件总数和较小多副杆数的可行解。

通过上述对构件总数和多副杆数的分析，对各评价指标进行加权，确定目标函数：

(3)

式中，f1为构件总数；f2为多副杆数(包括三副杆、四副杆等)，f2+1是为了防止存在f2值为0的情况，即多副杆个数为0；w1和w2分别为f1和f2的权重；a为调节系数。

3.5 选择策略

遗传编程中，个体被选择进行遗传操作的机会取决于其适应度值的大小，选择策略影响个体进化的速度和趋势。因此，个体过早收敛等问题的主要因素往往是由于选择策略的不当导致。

结合机构创新设计的特点，本文采用锦标赛选择法，锦标赛选择法的特点在于其以个体适应度的相对值为选择标准，能够有效地避免群体中个别或极少数特殊个体的影响，防止进化过程中发生早熟现象。

3.6 遗传操作

复制、交叉和变异是遗传编程的三种主要遗传操作。根据机构创新设计的特点以及实际设计过程中可能存在的问题，本文对遗传操作进行了改进。

(1)复制操作。从当前群体中，以适应度值的大小为指标，从种群中随机选择一个适应度值较大的个体作为亲代个体，该个体不经任何变化完整地复制到下一代群体中，具体步骤：①根据预先设定的概率随机选取群体中的个体Xi；②复制Xi得到X′i；③将个体X′i直接作为子代个体并保留。

(2)交叉操作。从当前群体中，以适应度值的大小为指标，从种群中随机选择两个适应度值较大的个体作为亲代个体，两个父代个体的不同部分重新组合产生新的子代个体，具体步骤：①随机选出两个个体Xi和Xj；②对Xi和Xj分别复制得到X′i和X′j；③对X′i和X′j分别随机选取交叉点，然后X′i和X′j交换交叉点的子树得到Yi和Yj；④若子代生成的个体为可行解则保留Yi和Yj，同时标记父代个体Xi和Xj已交配；若不是正确个体，则保留父代个体Xi和Xj并标记已交配；⑤检查是否群体中的所有个体都已经交配，否则返回步骤①。具体流程如图8所示。

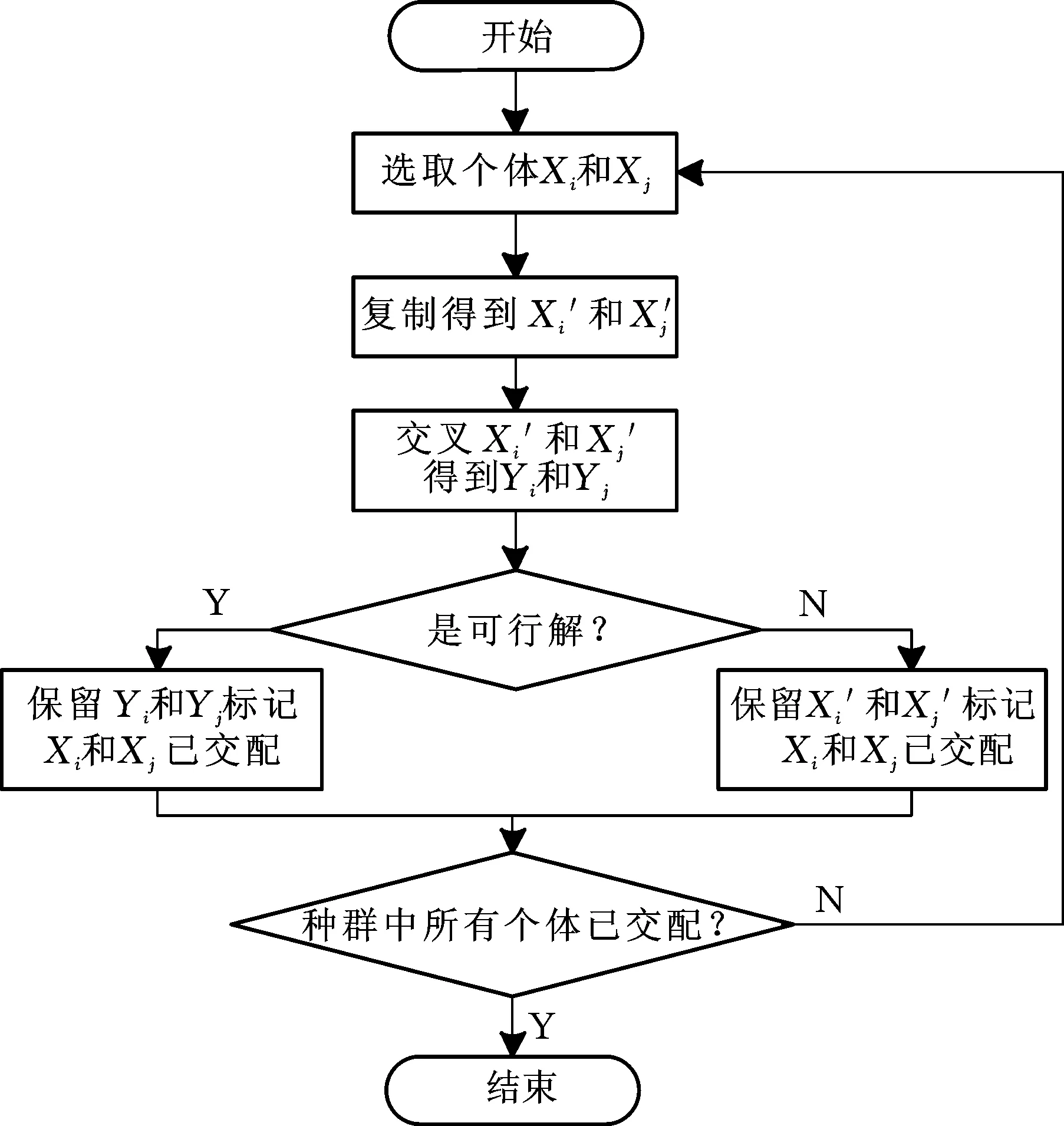
图8 交叉操作流程图Fig.8 Flow chart of cross

(3)变异操作。从当前群体中，以适应度值的大小为指标，从种群中随机选择一个个体作为亲代个体，该个体随机在某一结点处发生变异形成新个体，并将得到的新个体完整地复制到下一代群体中。具体步骤：①根据预先设定的概率随机选取群体中的个体Xi；②随机选取个体树上的一个结点(即突变点)，将突变点变异为另外一个适度大小的新子树，以取代该结点以下的子树而形成一个新的个体树X′i；③对新生成的个体X′i进行判断，若为可行解则保留，否则保留原有个体Xi。具体流程如图9所示。

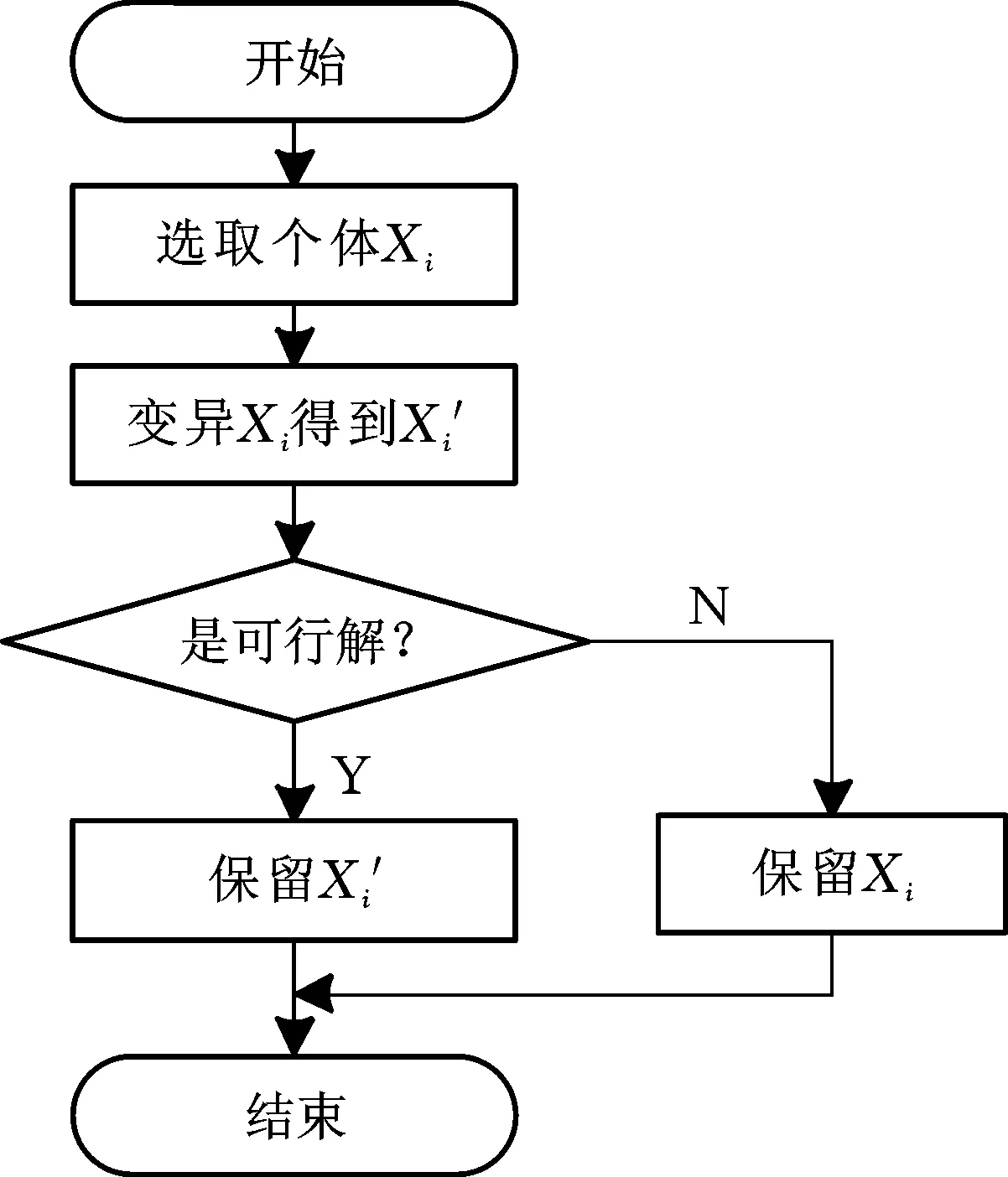
图9 变异操作流程图Fig.9 Flow chart of variation

3.7 终止准则及算法相关参数设定

遗传编程并行计算的本质在于：在适应度评价指标的驱动下，种群不断地适应环境的变化，向着对环境适应性更好的方向发展，若使算法停止则需给出终止准则。一般而言，常见的几种终止准则包括：达到最大进化代数或最大计算次数；经过n代后个体适应度值没有得到改善；得到满足问题预先设定解。

由于本文经过遗传操作得到的个体有些可能不符合设计要求与约束，因此采用预设最大进化代数为终止条件。

综上所述，该机构运动链创新设计进化方法需要设定的相关参数包括种群规模N、交叉率α、变异率β、进化代数n。

4 应用实例及结果分析

4.1 对比分析

为验证本文方法的有效性，以文献[13]中的锁芯机构创新设计为例，与再生运动链法进行对比分析。该文献中将玥玛空转锁芯一般化后，得到8杆10副单自由度一般化运动链。通过分析可归纳出该机构的设计要求与约束情况包括：①必备构件有机架、内圈杆、钥匙、弹片、整体键子、凸轮副；②内圈杆为三副杆或四副杆，弹片为三副杆，整体键子为多副杆；③机架与内圈有附随关系，同时机架不可能与钥匙有附随关系，内圈杆与叶片杆、钥匙存在附随关系，弹片与钥匙存在附随关系，整体键子与锁芯后节以及弹片存在附随关系，但与钥匙不存在附随关系。

整理以上设计要求和约束并给定相关信息：①机构的构件数量可变动范围为6～8；②多副杆数量不小于3。

使用再生运动链法进行设计时，考虑6杆和7杆的可能情况，做出如下分析：

(1)6杆单自由度：

F=3(nt-1)-2pt

(4)

通过式(4)计算得6杆单自由度时pt=7。综合构件总数和总运动副数得到6杆7副单自由度的所有可能杆件组合，如表3所示。

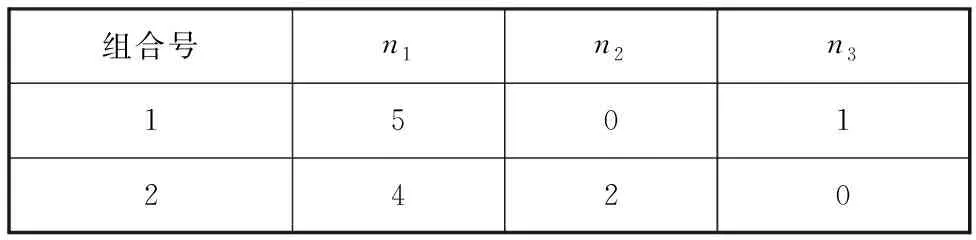
表3 杆件组合表

由于设计要求与约束中规定多副杆数量不小于3，而表3中组合均不满足设计要求，故排除6杆单自由度的可能。

(2)7杆单自由度。通过式(4)计算得7杆单自由度时pt=8.5。由于pt为正整数，故排除7杆单自由度的可能。

使用本文提出的机构运动链进化设计方法进行设计时，将设计要求中的各参数代入式(1)与式(2)，可得

(5)

(6)

式中，x22取3或4，x44≥ 3，且x44为正整数。

设定相关参数：种群大小为100，交叉概率为0.5，变异概率为0.3，进化代数设为20。

适应度函数根据式(3)，综合考虑所选评价因子(杆件总数和多副杆数)之间的权重比例，确保两个评价因子权重的平衡性，通过多组数据的计算，确定该组数据为最佳数据，式中各参数取值：a=1.5，w1=8，w2=1。

选取必备构件钥匙为个体树的根，结合设计要求，最终得到最佳个体如图10所示。个体树中各结点的信息整理如表4所示。

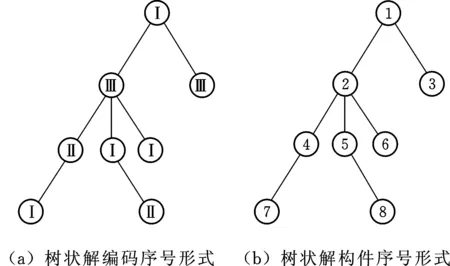
图10 锁芯机构最佳个体树Fig.10 Optimal individual of locking mechanism

构件号运动副数构件号运动副数1224324352627283

最终，结合设计要求和约束以及表4中的信息，可将图10的最佳个体树转化为图11中的一般化链。该结果与文献[13]中通过再生运动链法设计的结果相同。

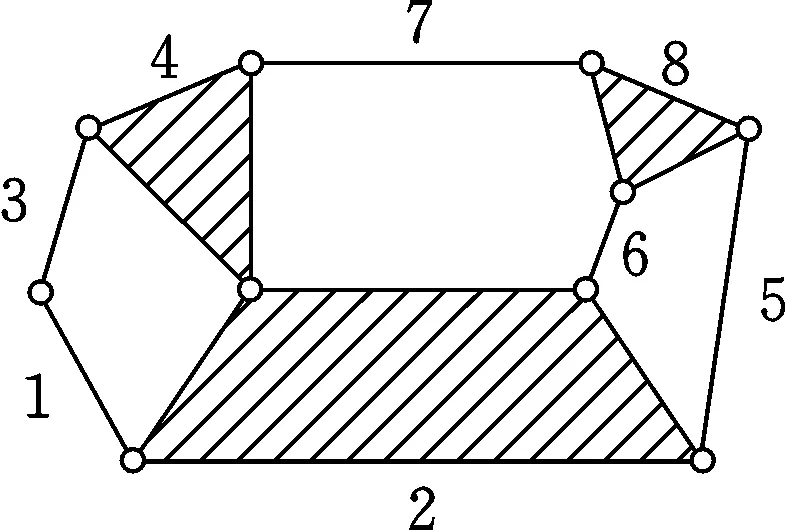
图11 锁芯机构最佳个体一般化链Fig.11 The generalized kinematic chain of optimal individual of locking mechanism

4.2 案例应用

下面以一种玻璃模具开合机构为例，利用本文方法进行创新设计。该玻璃模具开合机构简图见图12，它是一个12杆16副单自由度机构，由驱动件液压缸和各杆件的相互作用，实现模具的开合动作。

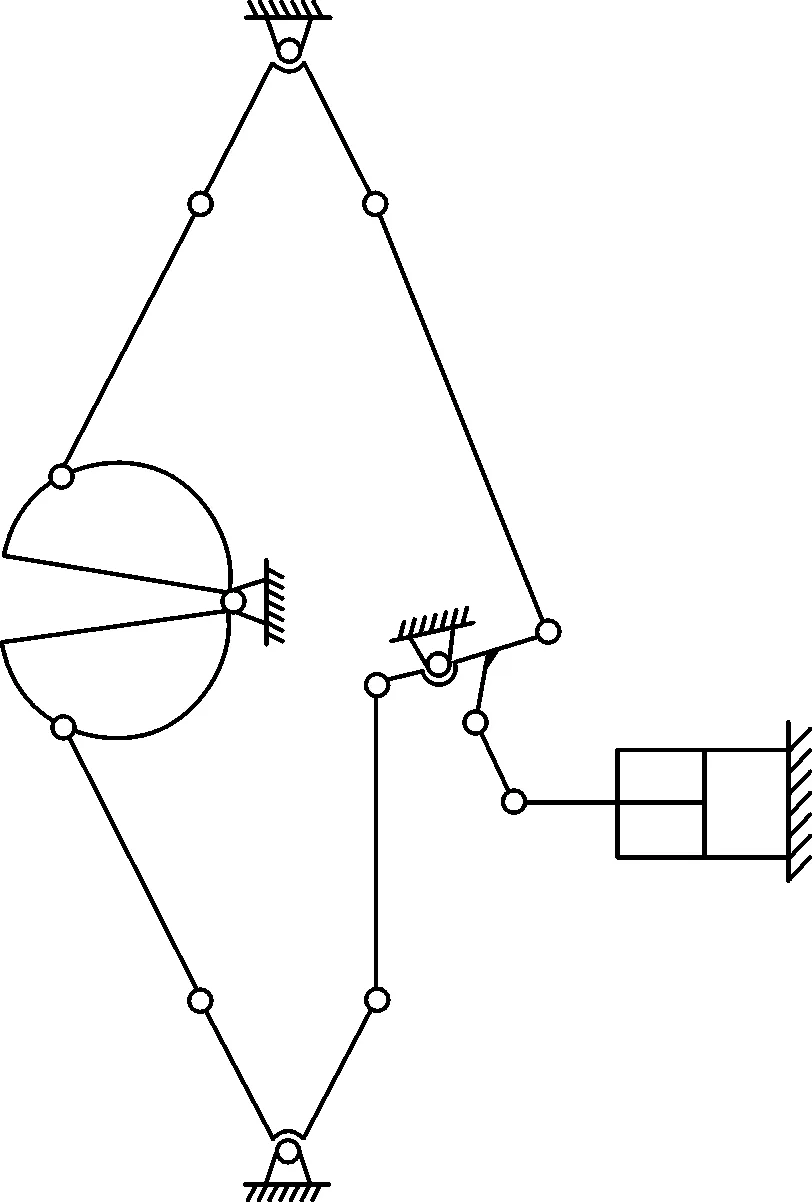
图12 玻璃模具开合机构简图Fig.12 A schematic diagram of retractable mechanism of glass mold

首先对原机构的功能特性进行分析，确定该玻璃模具开合机构的设计要求与约束如下：①必备构件有模具、液压缸、机架、两个三副杆且其中一个必与机架关联；②机架的运动副数大于等于3；③模具与液压缸必定不附随。将设计要求中的参数代入式(1)、式(2)，可得

(7)

(8)

式中，x11为不小于3的正整数。

接着选取必备构件液压缸为个体树的根，并给定相关参数：种群大小为100，交叉概率为0.5，变异概率为0.3，进化代数设为20。适应度函数根据式(3)，式中各参数取值：a=1.5，w1=8，w2=1。结合设计要求，最终得到最佳个体如图13所示。

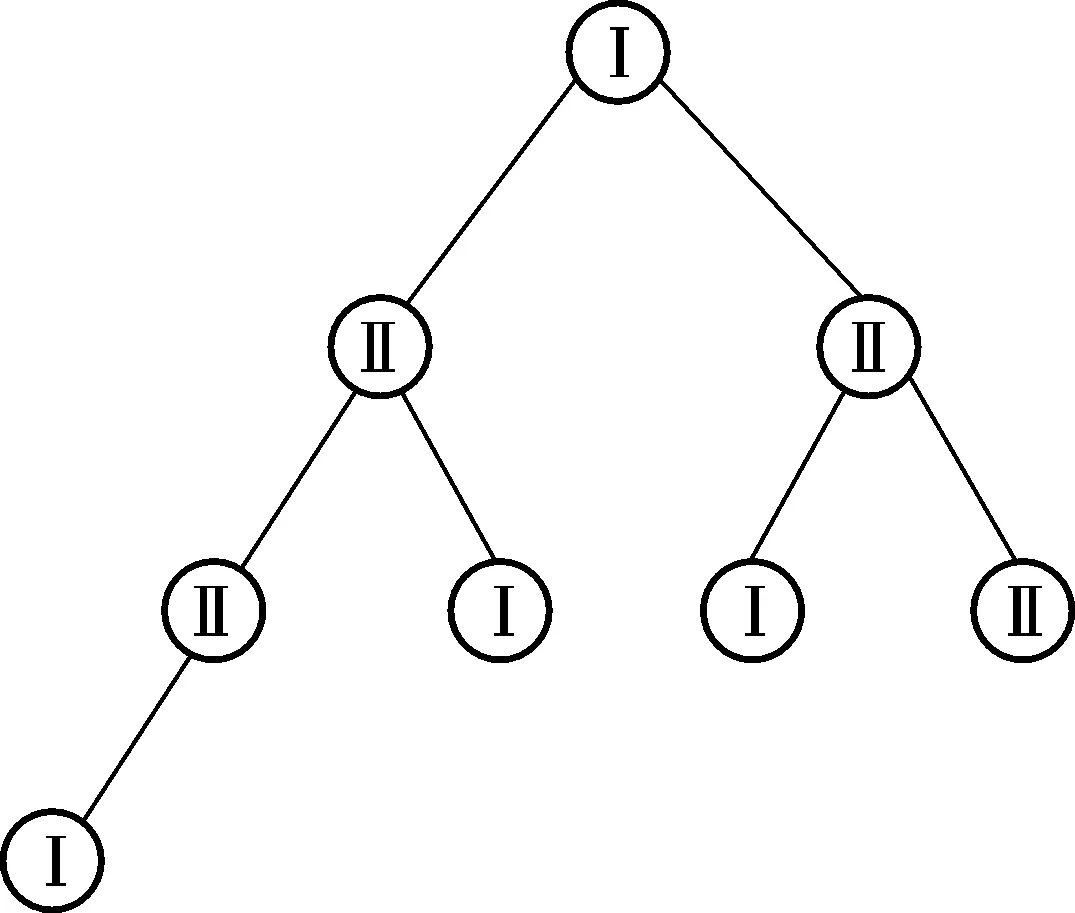
图13 开合机构最佳个体树Fig.13 Optimal individual of retractable mechanism

结合设计要求和约束以及表1中的信息，可将图13的最佳个体树转化为图14中的一般化链。并将该一般化链结合设计要求经过具体化规则，得到图15所示8杆10副单自由度的新机构。实践证明，新机构为符合设计要求的可行解，同时新机构与原机构相比，总杆数由12减少至8，总运动副数由16减少至10。

图14 开合机构最佳个体一般化链Fig.14 The generalized kinematic chain of optimal individual of retractable mechanism

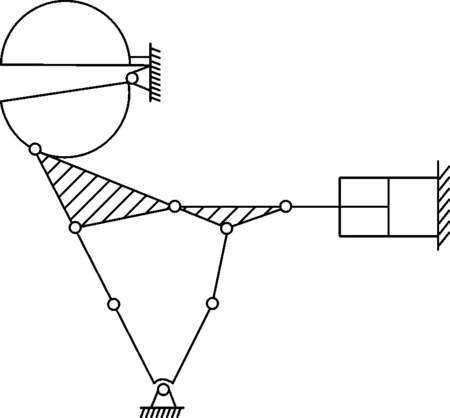
图15 新机构具体化简图Fig.15 Schematic diagram of the materialization of new mechanism

对比分析新机构和原机构的运动特性可得：新机构上模具与机架焊接，通过液压缸的驱动和各杆件的相互作用，带动下模具转动，从而实现模具的开合动作。通过这一案例验证了新机构和原机构具有相同的功能和效果。

5 结论

(1)采用遗传编程替代数综合方法，在保证新机构满足原机构功能特性的条件下，实现新机构与原机构不同构件数和运动副数的进化设计。

(2)结合线性代数和图论的内容，将可行解的杆件和运动副数组合与杆件间的附随关系分别通过不等式方程组和拓扑邻接矩阵的方式表达，结合两种约束形式，建立具有通用性的数学模型。

(3)结合实际问题对进化算法进行优化改进，分别设计了合适的编码解码方式、适应度评价函数以及合理的遗传操作，确保整个方法流程的合理运行。

(4)本文的研究为机构运动进化设计提供了一种可行的方案，但仍存在一些问题有待研究。例如，可根据生产实际的需求，对适应度评价函数进行改进，考虑增加更实际的适应度评价因子，使设计的最佳个体品质更优良，以及本文提出的方法是否适用于所有的机构创新设计还有待进一步验证。