单晶铜纳米压印亚表层晶体结构演变机理

王全龙 张超锋 武美萍,2 陈家轩

1.江南大学机械工程学院，无锡，2141222.江苏省食品先进制造重点实验室(江南大学)，无锡，2141223.哈尔滨工业大学机电工程学院，哈尔滨，150001

0 引言

纳米压印技术是制造纳米级表面微结构的重要手段，被广泛应用于微电子、传感器、光学精密仪器及航空航天等领域。而制造过程中引入的材料亚表层晶体损伤严重影响着微纳结构件的加工精度及力学性能，制约着武器装备及高精度仪器仪表的使用性能及寿命[1-3]。因此，研究纳米压印过程中基体材料的亚表层损伤形成机制及探讨亚表层材料晶体结构演变机理具有重要意义。

国内外学者广泛采用分子动力学(molecular dynamics,MD)仿真方法研究纳米压印过程，如KIM等[4]采用分子动力学研究了单晶铝及金的纳米压印，定性研究了压头附近晶体的初始塑性变形。VLIET等[5]研究了单晶材料的纳米压印过程，给出了材料发生塑性变形的定量判据。LIU等[6]基于分子动力学仿真方法系统地研究了金刚石压头和单晶金基体在不同加载力、不同温度及不同加载速率下的压印过程，以及不同参数对压印过程中材料变形行为的影响。ZIMMERMAN等[7]开展了纳米压印过程仿真和实验研究，分析了纳米压印过程中产生的表面台阶形貌和位错形核及其演化。DIAO等[8]分析了晶体材料各向异性对纳米压印力学性能的影响。WANG等[9]研究了压印过程中位错形核与晶界的交互作用过程。MA等[10]基于纳米压痕实验对单晶铜和多晶铜纳米压痕后的材料强度进行了对比，发现多晶铜材料强度优于单晶铜强度。ZHANG等[11]采用分子动力学仿真研究了单晶硅压印过程，探讨了压印过程中材料初始塑性阶段的位错和相变相关作用机理。

LI等[12]进行了单晶硅各向异性的纳米压印实验研究，分析了材料的各向异性对材料力学性能及压印后表面形貌的影响。赵鹏越等[13]采用分子动力学仿真研究了纳米压印过程中微观结构对多晶铜力学特性及变形机理的影响机制。ZHU等[14]研究了在纳米压印过程中单晶硅基体的变形机理，研究发现压印时材料内部出现位错、空位及滑移带，压头撤离时，基体表面出现径缩现象。靳巧玲等[15]开展了Ti金属薄膜的纳米压印研究，探讨了溅射功率对薄膜显微结构和力学性能的影响机制。陈坚等[16]采用纳米压痕仪系统地开展了多晶铜在不同加载速率下的微纳尺度力学和蠕变性能变化的实验研究，分析了纳米材料的硬度、弹性模量及蠕变指数的变化规律。

由上述分析可知，目前的研究工作主要集中在表征纳米压印过程中工件发生的塑性变形，以及工件材料的位错形核机理及缺陷演化过程。由于缺乏合适的晶体结构识别技术，目前对于微纳构件亚表层晶体结构演变的研究还鲜有人涉及，而材料的微观晶体结构影响并决定其力学性能，制约着所制造微纳构件的性能。因此本文基于球谐函数分析技术，开发出晶体结构表征方法，并将其应用于微纳构件纳米压印过程的研究中，分析构件亚表层晶体结构演变；结合改进的中心对称参数法研究纳米压印过程中微纳构件位错缺陷区域对应的微观晶体结构变化，以此来表征亚表层中不同晶体结构的变化规律。

1 仿真模型及分析方法

1.1 仿真模型构建

本研究所建立的分子动力学模型中，压头材料为金刚石，基体材料为单晶铜。仿真中采用Morse势函数计算压头中碳原子和基体中铜原子间的相互作用，采用EAM势计算铜原子间的作用，采用Tersoff势函数计算碳原子间的相互作用。

Morse势函数[17]：

u(rij)=D[e-2α(rij-r0)-2e-α(rij-r0)]

(1)

式中，u(rij)为原子i、j间的对势；r0为平衡位置的原子间距；α为弹性模量；D为结合能；rij为原子i、j间的距离。

仿真中采用的C-Cu原子间的Morse势函数参数[17]见表1。

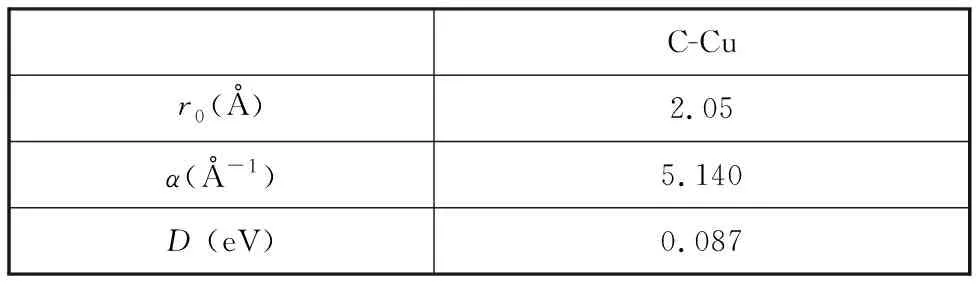
表1 C-Cu原子间的Morse势函数参数

EAM势函数用原子间对势能以及原子核嵌入能两部分来计算原子的总势能，因此被广泛应用于描述金属原子间的相互作用关系。具体的势函数如下[18]：

(2)

(3)

式中，Fi为原子i嵌入能；N为原子总数；ρi为其他原子i处的电子云密度；ρj为原子j在原子i处产生的电子密度函数。

Tersoff势函数是被用于精确计算共价体系原子间作用的势能函数，本研究中压头为金刚石材料，是共价键晶体材料，因此采用Tersoff势函数来计算原子间的势能，具体计算公式如下[19]：

(4)

Vij=fc(rij)[V′R(rij)+bijVA(rij)]

(5)

式中，fc(rij)为原子间相互作用的截断函数；VA(rij)为吸引项对偶势函数；V′R(rij)为排斥项对偶势；bij为调制函数。

本研究中建立的仿真模型如图1所示，模型尺寸为35a0×22a0×35a0，其中a0为单晶铜的晶格常数，采用半球形压头。工件采用Nose-Hoover热浴法进行温度控制，Y方向采用固定边界条件，X和Z方向采用周期性边界条件，以减小因模拟规模产生的尺寸效应。具体参数如表2所示。

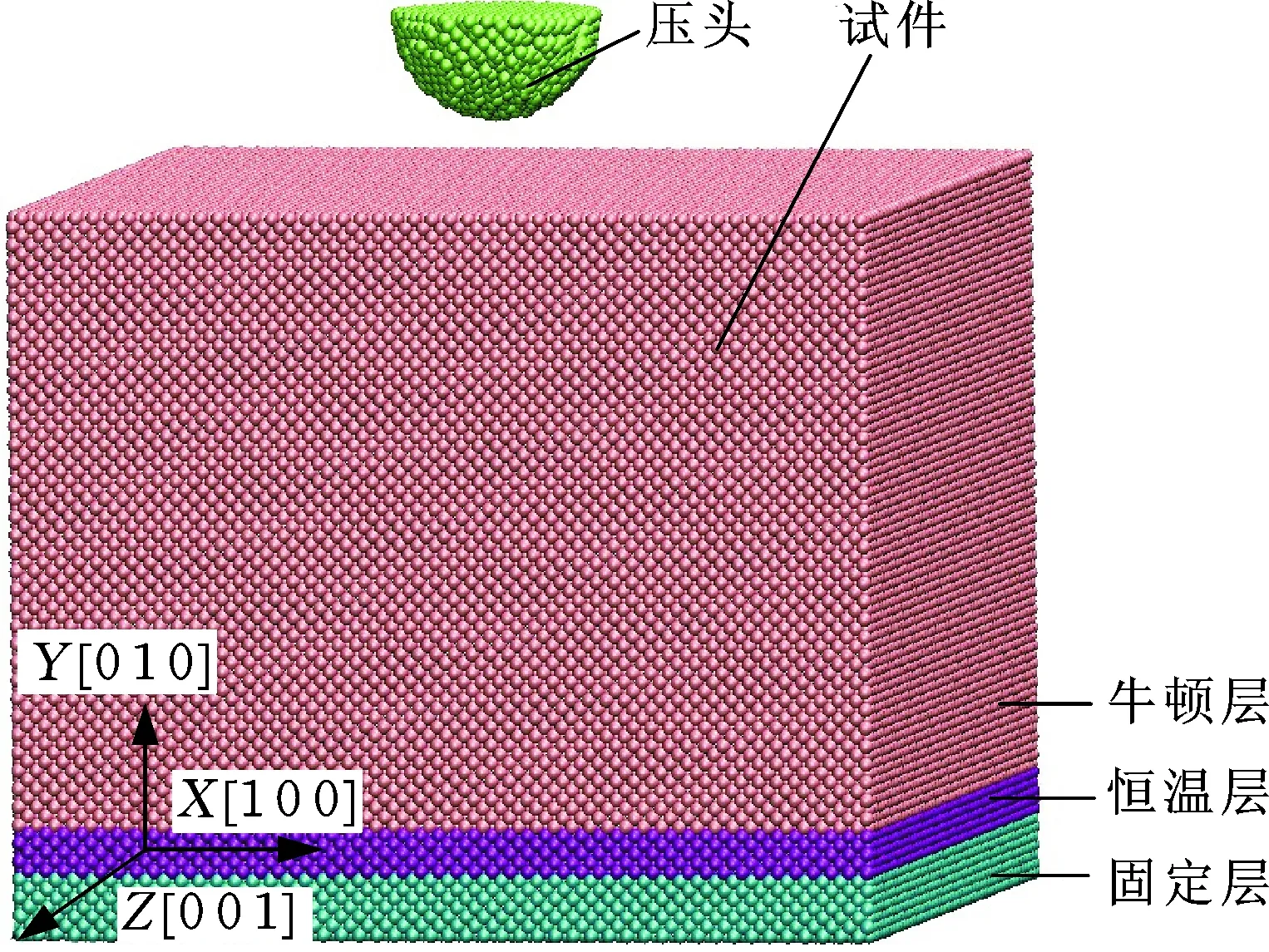
图1 仿真中所用的MD模型Fig.1 MD Model in simulations

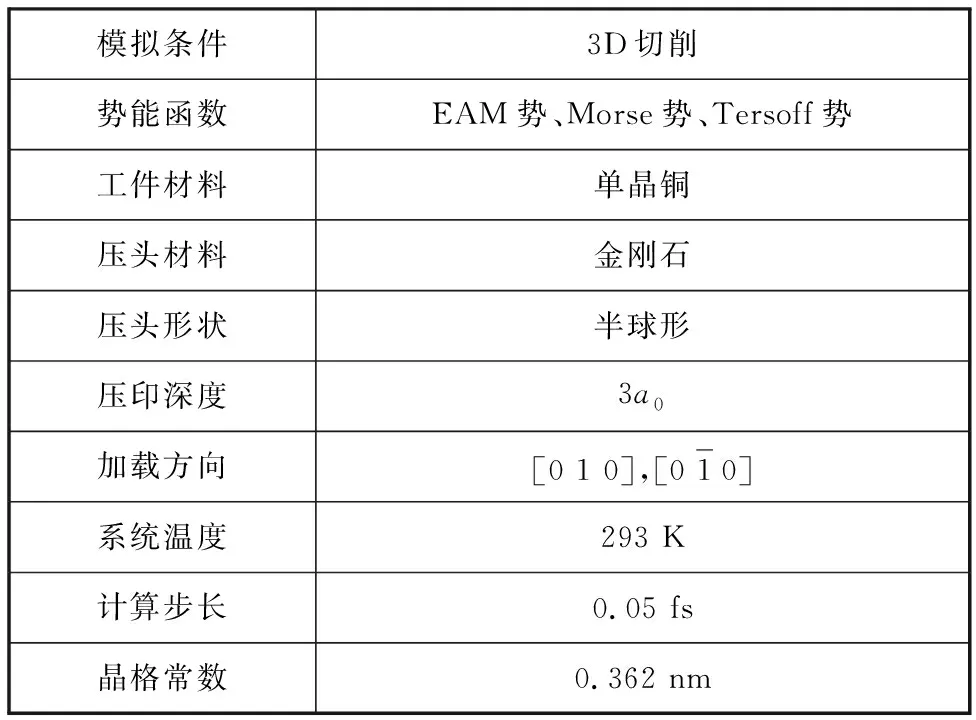
模拟条件3D切削势能函数EAM势、Morse势、Tersoff势工件材料单晶铜压头材料金刚石压头形状半球形压印深度3a0加载方向[0 1 0],[0 1 0]系统温度293 K计算步长0.05 fs晶格常数0.362 nm

1.2 缺陷分析方法

本研究采用中心对称参数法(centro-symmetric parameter,CSP)分析基体材料内部的位错形核及缺陷演化。对于具有面心立方(face-centered cubic,FCC)结构的单晶铜材料，通过下式[20]计算每个原子的CSP值：

(6)

式中，Ri为长度相同的近邻原子对；Ri+6为方向相反的近邻原子对。

理想FCC晶体的CSP值为0；当晶体材料发生较大变形时，CSP值就会变大。因此可用CSP值的大小表征材料局部晶格的无序状态，区分出完好晶格原子和存在局部缺陷的原子。但由于表面原子与内部原子的近邻原子对数目不同，导致采用CSP值分析时表面原子与缺陷原子混淆。因此本文通过改进中心对称参数法来滤除表面原子的影响，优化后的中心对称参数[21]：

(7)

式中，Ri0、Ri0+6为初始状态时长度相同、方向相反的近邻原子对。

中心对称参数法能识别晶体材料的内部缺陷，但不能准确表征材料原子的晶体结构状态。因此笔者采用球谐函数方法来表征材料的晶体结构。对于特定结构的晶体材料，其球谐函数值为某一特征值，可以根据球谐函数的不同取值来识别材料的晶体结构。该算法更复杂也更精确，能精准地区分不同材料的晶体结构状态。本研究通过编制球谐函数值的计算程序，在建立不同晶体结构的模型基础上，计算和完善了球谐函数的基础数据值。结合可视化技术和数据处理技术，可以直观全面地分析材料的晶体结构变化。球谐函数值[22]：

(8)

(9)

式中，l为球谐基函数参数，本文中取l=6；Nb为最近邻原子数目；Ylm(θi,φi)为勒让德多项式；θi和φi为球坐标系中的角度变量。

本研究通过计算获得几种理想晶体结构的球谐函数值，如表3所示。而实际材料中由于存在原子振动，同一种晶体结构的球谐函数值会有小幅波动，本研究中同样给出经过MD弛豫后球谐函数值的波动范围，如表3所示。纳米压印仿真可以得到基体材料原子的位置坐标信息，再利用所编制的球谐函数值计算程序求得每原子球谐函数Q6，并将其与基础数据进行

表3 特征晶体结构球谐函数Q6标准值及波动范围

比较，就可以获得压印后基体材料的晶体结构状态，然后可探讨纳米压印过程中材料表层及亚表层晶体结构演变机理。

2 仿真结果和分析

基于所建立模型进行纳米压印过程的MD仿真。首先将模型进行能量最小化计算，以优化模型消除不合理因素，然后对压印系统进行MD驰豫，使其达到稳定状态，随后给压头施加载荷，使其沿加载方向按设定速度压印至3 nm，加载完成后给压头施加反向载荷进行卸载，压头开始反向运动至最初位置。仿真得到的加载过程纳米压印系统图像如图2所示，图中原子按改进后中心对称参数Pg的不同取值进行着色。

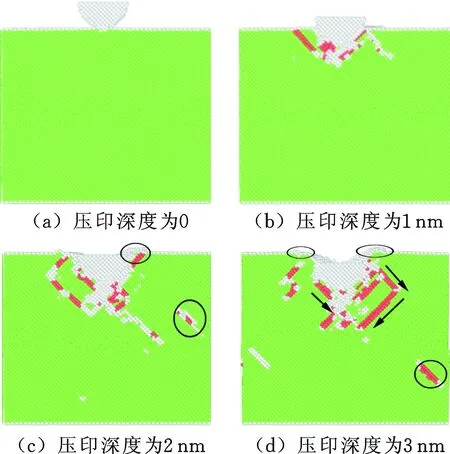
Pg取值为位错缺陷的特征值 未变形的面心立方结构原子 变形较大的未知结构或表面原子图2 纳米压印加载过程的位错缺陷演化图Fig.2 Dislocation defect evolution of loadingprocess in nano-indentation

由图2可知，纳米压印过程中，在载荷的作用下，压头持续向下运动，当压头接触基体材料后，单晶铜试件开始变形，试件原子的变形是由载荷对基体材料做功引起的，如图2a所示。随着压头逐渐下压，试件原子晶格变形产生能量积聚，当积聚的变形足够使原子脱离周围晶格上原子的束缚时，单晶铜试件原子发生跃迁，导致初始的位错形核；在压头持续的挤压下，形核的位错迅速扩展成堆垛层错，如图2b所示。当压头继续下压到压深2 nm时，如图2c所示，基体材料发生位错发射，压头下方形核的位错像子弹一样被发射到试件内部，在试件的内部形成晶体缺陷；基体材料也由原来的弹性变形逐渐变为塑性变形，并在试件表面出现原子台阶和材料的堆积。在载荷作用下，压头继续下压至3 nm，压头下方的基体材料由于受到压头的持续挤压而产生严重塑性变形，基体表面材料堆积增多，原子台阶变高，基体内部位错缺陷的规模增大，位错扩展更加充分，沿{1 1 1}滑移系的两个滑移方向均有堆垛层错产生，如图2d所示。

Pg取值为位错缺陷的特征值 未变形的面心立方结构原子 变形较大的未知结构或表面原子图3 卸载过程不同压印深度的原子瞬时图像Fig.3 Dislocation defect evolution of unloadingprocess in nano-indentation

图3是纳米压印卸载过程的位错缺陷演化图像，图中原子配色方案同图2。卸载过程给压头施加向上的力，压头从压印深度3 nm处开始向上运动，如图3a所示。由图3可以看出，随着压头逐渐抬升至2 nm时，基体内部的位错缺陷逐渐湮灭，堆垛层错的数量大幅下降，在位错形核区域发射出去的位错缺陷逐渐向反方向运动，最终与压头下方的位错缺陷融合，如图3b所示。随着压头继续抬升，在压印深度为1 nm时，压头下方的位错缺陷规模继续减小，出现了较稳定的V形位错缺陷结构，V形位错外部还存在少量晶体缺陷，如图3c所示。由于单晶铜材料的黏弹性，压头下方受挤压变形的材料在压头抬起后发生弹性恢复，但仍有一部分材料原子附着在压头下表面，而附着在压头上的材料原子在压头继续抬起时会在基体表面向外扩展，而在基体表面形成原子台阶，如图3d所示。当压头脱离基体时，仍有很多原子附着在压头表面，而在基体表面并没有形成凹坑，这是由于变形材料原子在位错缺陷演化的影响下以原子台阶的形式平铺在基体表面而形成的。最终会导致基体表面残留原子台阶，压印区域表面变粗糙，而在基体内部仍残留了V形位错。

笔者研究了V形位错的形核演化机理。图4为纳米压印中形成的V形位错轴侧视图和原理示意图。由前述分析可知，V形位错在压头下方形核，形核后的V形位错扩展到表面及模型边界，在基体表面残留位错线。图4b为V形位错形核过程原理示意图，可知，位错分别在压头下方A、B处形核并向基体内部扩展，当两个位错扩展到N时相互阻碍形成位错锁N。位错锁N阻碍了两个部分位错的扩展，使得两位错沿垂直于原扩展方向发生位错攀移而形成梯杆位错R。在梯杆位错R上方扩展的两个位错最终演化为两个堆垛层错S1和S2， S1、S2和R共同组成稳定的V形位错而最终残留在基体的亚表层。该仿真结果与文献[23]的实验结果相似，如图5所示。该研究采用STM进行FCC单晶金纳米压印过程，研究了压印后试件的表面形貌，并采用原理示意图探讨了V形位错的形成机理。

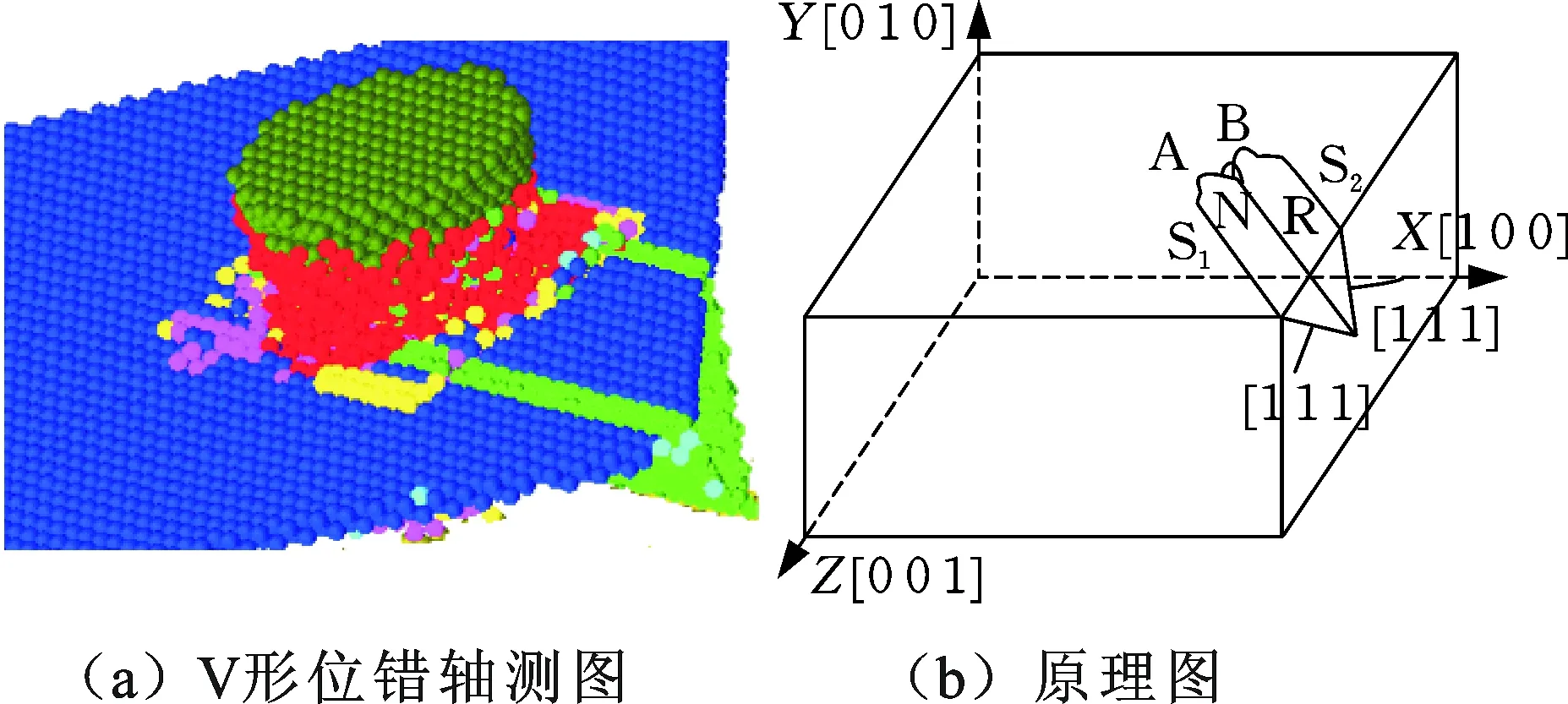
图4 V形位错环及其原理示意图Fig.4 The V-shaped dislocation loop and itsschematic diagram

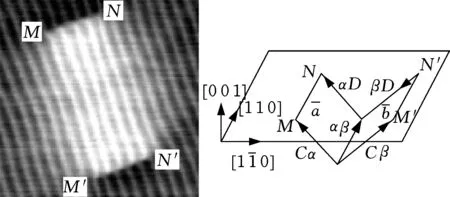
图5 纳米压印V形位错STM图像及原理示意图[23]Fig.5 STM image of nanoindentation and schematic diagram of V-shaped dislocation[23]

图6是纳米压印过程作用在压头上的载荷-位移曲线，其中压头所受载荷方向向上为正值、向下为负值，压头位移是指压头移动的距离，0～3 nm为加载过程，其余为卸载过程。由分析载荷位移曲线的波动情况可知，加载过程载荷和压头位移基本成比例增加，这是因为材料变形处于弹性变形范围内，局部的载荷波动是由于材料变形积聚和位错形核释放导致的。压印过程初始载荷为负值，是由于加载过程压头匀速下压，当接近基体表面约0.3 nm时，压头原子与基体原子存在较大的范德华引力，为保持匀速下降，需给压头施加一个向上的力(为负值)。继续下压时基体材料变形产生远大于范德华力的变形抗力，导致载荷开始变为正值，加载过程最大载荷达250 nN。卸载过程压头向上运动，所施加载荷方向应向上，而由载荷位移曲线可知施加的载荷先为正后逐渐变为负值，这是由于卸载初始阶段，变形的基体材料弹性恢复给压头一个向上的力，要保持压头匀速抬起，此时需要施加一个向下的力(为正值)。随着变形的逐渐恢复，这个力逐渐变小直至消失，施加在压头上的力变为负值，先变大后变小，这是附着在压头表面的原子与基体材料间的相互作用力导致的，整个卸载过程最大载荷为150 nN。卸载过程中压头位移大于7.5 nm后，施加在压头上的载荷才变为0，这是由于压头抬起时表面黏附的原子和基体材料存在相互作用的范德华力，只有当压头抬起距离基体表面2 nm左右，这种范德华力作用才消失，载荷才变为0。

图6 纳米压印过程载荷-位移曲线Fig.6 Load-displacement curve of nano-indentation

为了更清晰地表征压印后工件内部缺陷分布及位错形核与扩展，将具有面心立方结构的原子隐去，并将未知结构的原子按Pg值大小进行细分，如图7所示。纳米压印过程中，试件原子在压头的挤压下发生局部位置迁移，以压头为中心的几层铜原子发生了塑性变形，形成堆垛原子区域，原子间势能逐渐增大，使得变形的Cu原子所具有的迁移能增大；当原子迁移能达到一定水平时，就会使Cu原子有足够的能量脱离原来的晶格格点位置，导致位错初始形核并扩展运动。由图7 a可以看出，位错沿[-1 0 -1]方向扩展；由图7a和图7b可清晰地看到压印过程中位错形核后沿着滑移面运动，位错滑移面均属于{1 1 1}滑移系统。

图7 基体材料纳米压印亚表层缺陷分布图Fig.7 Subsurface defect distribution in nano-indentation

采用球谐函数分析法研究纳米压印后基体材料的晶体结构演变，将每个原子截断半径内的第一近邻原子详细信息全部筛选出来组成最近邻原子列表，然后把最近邻原子列表的信息输入球谐函数计算子程序，可以求得每个原子的球谐函数Q6值，最后采用可视化软件将基体原子按球谐函数值着色，得到纳米压印后单晶铜基体材料每个原子所处的晶体结构状态，如图8所示。图中8a和图8c为球谐函数表征的晶体结构状态，图8b和图8d为对应时刻中心对称参数表征的基体位错缺陷分布。图8a和图8c中，图中A表示的晶体结构为缺陷面心立方(deformed face-centered cubic，DFCC)结构，其球谐函数值在0.530～0.552以及0.575～0.590之间；B为密排六方(hexagonal close-packed，HCP)结构，其球谐函数值在0.460～0.490之间；C为正20面体(icosahedron，ICO)结构，其球谐函数值在0.665～0.695之间；D表示未发生晶体结构转变，仍为面心立方晶体结构；E为表面原子，晶体结构未发生改变。

由图8可以看出，压头下方位错形核区域的原子晶体结构变化较大，有较多原子从FCC转变为ICO和HCP，而在位错扩展区域，基体材料的结构均为DFCC结构。这是由于压头下方基体材料受到压头的挤压作用显著，从而发生剧烈变形，导致单晶铜原子排列更为紧密，使其晶体结构从原子排布疏松的FCC结构转变为原子排列更密集的HCP和ICO结构。对于位错扩展区域，原子迁移的距离仅为一个博格斯矢量(1/6a0)大小，远小于压头下方的材料变形量，因此位错扩展区域材料晶体结构主体仍为FCC，只是会有个别原子窜动，导致理想面心立方结构中有1～2个原子发生错动(如图8中A所示的微观结构)，从而变成DFCC结构。

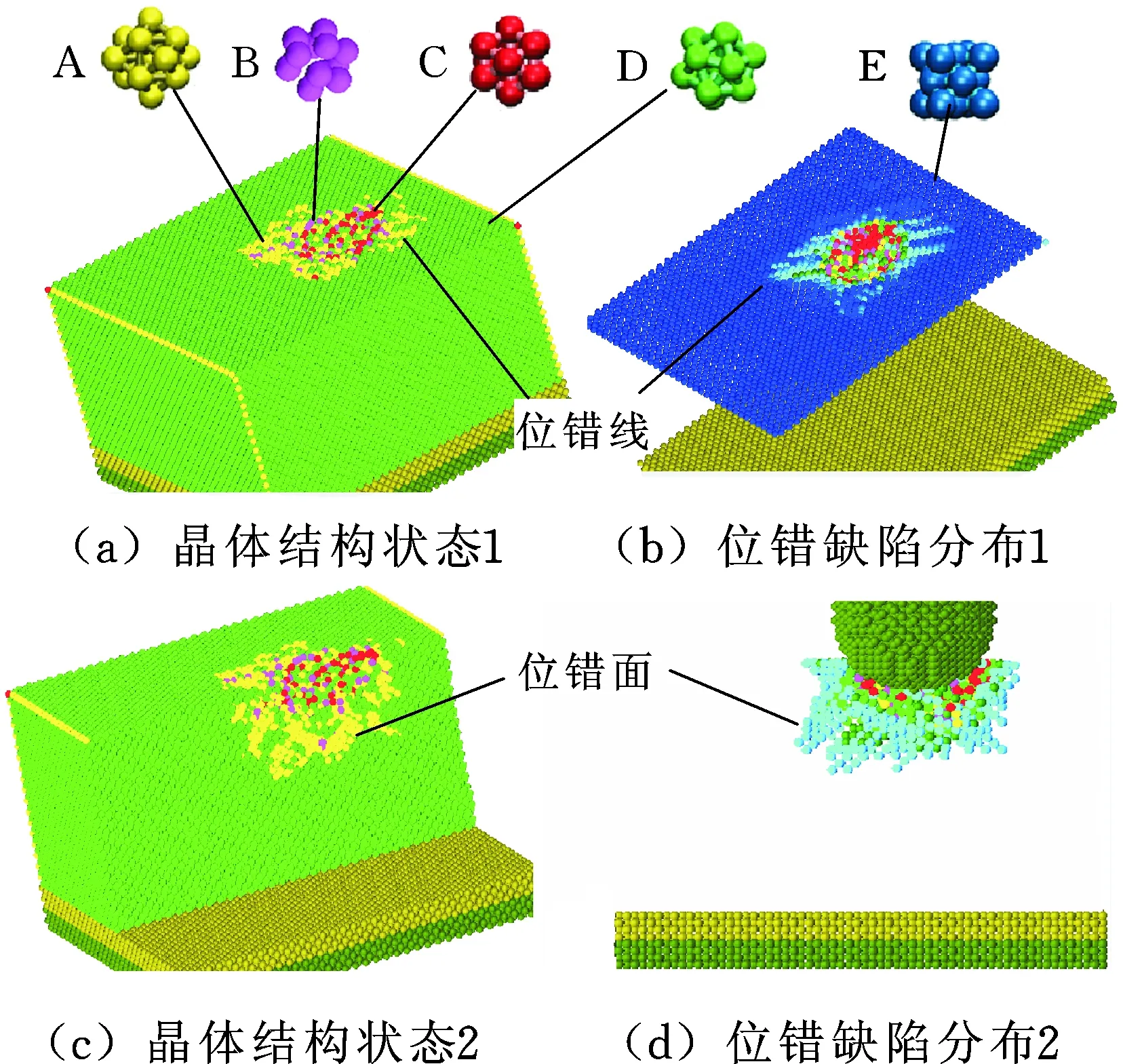
图8 基体材料晶体结构状态及对应的位错缺陷分布Fig.8 Crystal structure and its dislocation distribution of basis material

图9 不同压印深度时特征晶体结构原子数目Fig.9 The numbers of crystal structural atomsunder different indentation depths

为了进一步研究压印过程中不同晶体结构演变规律，笔者对不同压印深度下基体材料中存在的各种晶体结构原子数目进行了详细统计，并绘制出不同晶体结构原子数目随压印深度的变化曲线，如图9所示。由图可知，在压印初期ICO与HCP原子数目与DFCC结构原子数目相差不大，在压印深度达到3 nm后，DFCC结构原子数目明显增加，且占主要部分，ICO和HCP结构的原子数目也在增加，但增幅不明显。这说明，在压印初期就存在位错形核及位错扩展，但规模较小，导致发生结构转变的原子数目较少；而压印深度达到3 nm后，位错形核及扩展的规模均较大，导致各种晶体结构原子数目均有增加，另外由于该时期压印区域的位错运动主要为远离形核区域的位错扩展，而位错扩展后工件材料的晶体结构大部分转变为DFCC，导致DFCC增幅最显著。

3 结论

(1)单晶铜纳米压印过程中，压头对试件的挤压作用导致材料发生变形，随着材料变形能积聚到一定程度后导致位错形核，位错形核首先发生在压头下方并沿{1 1 1}滑移系滑移运动；压印后的基体材料表面有原子台阶残留，亚表层存在V形位错环等典型缺陷结构。

(2)单晶铜纳米压印加载过程中，压头上载荷与压头位移成比例增加，局部载荷波动是由于材料变形积聚和位错形核释放导致的。由于材料弹性恢复给压头向上的力，导致初始卸载阶段中压头上的载荷方向与卸载方向相反；由于压头表面黏附铜原子与基体间的相互作用，使得压头抬离基体2 nm左右时卸载载荷才减小为0。

(3)纳米压印后，压头下方位错形核区域的基体材料，其晶体结构由FCC转变为排列更为紧密的HCP和ICO结构；位错扩展区域的材料晶体结构转变为DFCC结构。随着压印深度的增大，基体材料转变为3种晶体结构的原子数目均增多，DFCC结构的原子数目增加最为显著。