灵活“构造圆”,巧妙来解题
☉河南省西平县基础教育教研室 郭长军
在解决数学几何问题时,我们通常想到的解决方法是由问题的条件到相应问题的结论之间的定向思考,但是对于某些问题采用这样的思考方式来解显得比较困难,甚至无从着手,在这种情况下,我们不妨改变一下思维策略,寻找一个中间桥梁,以此寻到一条绕过障碍的新途径.例如,对于已知某些几何问题中给出直角三角形的斜边固定不变,而直角顶点时刻在运动变化;或给出几个点到某一个定点的距离相等;或给出一个等腰三角形绕着其中一个角的顶点旋转;亦或给出两个公用斜边的直角三角形等问题,我们可以通过构造圆,巧妙地利用圆的有关知识及已学过的其他数学知识把问题解决.在运用构造圆的方法解题时,一要明确构造的目的,即为什么目的而构造,二要弄清楚问题的特点,以便依据特点,实施构造.通过以下几个具体典例,可以尝试从中总结规律,提高自己运用构造圆的方法解决实际问题的能力.下面我初步谈一谈可以构造圆的几种常见类型:
一、如果遇到直角三角形的斜边不变,而直角顶点时刻发生变化的直角三角形,可以构造以斜边为直径的圆

图1
典例分析1:(2013武汉)如图1,已知正方形ABCD中,AB=2,E、F是AD上的动点,且AE=DF,连接CF交BD于点G,连接AG交BE于点H,连接DH,则线段DH长度的最小值是___________.
【分析与解答】可以证明△AEB△DFC,所以∠ABE=∠DCF,再证明△ABG△CBG,所以∠BAG=∠BCG,得到∠BAG+∠ABE=∠BCG+∠DCF=90°,即∠AHB=90°,也就是说,△ABH是斜边AB固定不变,但直角顶点H时刻发生变化的直角三角形,根据直径所对的圆周角是直角,构造以AB为直径的圆O,则点H始终在⊙O上运动.要使DH最小,则连接OD,交⊙O于H,那么点H就是所求的点.
因为四边形ABCD是正方形,AB=2,所以AD=2,OA=OB=1.
评析:经分析可得∠AHB=90°,△ABH是直角三角形,而斜边AB始终不变,直角顶点H发生变化,所以可以构造以AB为直径的圆.

图2
二、如果遇到一动点到定点的距离始终相等,那么可以构造以定点为圆心、以动点到定点的距离为半径的圆

图3
典例分析2:如图3,菱形ABCD的边AB=8,∠B=60°,点P是AB上一点,BP=3,点Q是CD边上一动点,将四边形APQD(DQ≠AP)沿直线PQ折叠,点A的对应点为M,当CM的长度最小时,CQ的长为___________.
【分析与解答】解决这个问题的关键是找出折叠后哪个位置使CM最短.由于将四边形APQD沿直线PQ折叠,点A的对应点是M,根据折叠前后图形全等,可知AP=MP,点P是定点,点M是动点,但点M到点P的距离始终等于AP的长,所以,以点P为圆心,以AP的长为半径画圆,点A的对应点M始终在这个圆上.

图4
由图4可得,连接PC,交圆P于点M,则此时CM最短.
过点C作CN⊥AB于点N.
由四边形ABCD为菱形,AB=8,得BC=8.
又BP=3,则NP=1.
在Rt△CNP中,CP=7.
由折叠前后对应角相等,得∠APQ=∠MPQ.
由CD∥AB,得∠APQ=∠PQC,则∠MPQ=∠PQC,则CQ=PC,则当CM的长度最小时,CQ的长为7.
评析:由于本题中的点P固定,点A与点P之间的距离是一个定值,根据题意将四边形APQD沿着直线PQ折叠,不管怎样折叠,点A折叠后的对应点M到点P的距离始终等于线段AP的长.所以通过构造以点P为圆心、以AP为半径的圆,结合圆外一点到圆上最短距离问题的解法就是连接该点和圆心,与圆的交点就是使该点到圆的距离最短的点,从而巧妙地找出点A沿直线AP翻折后的对应点,进而把问题解决.
三、如果遇到将一个等腰三角形绕其中一个角的顶点旋转,可以构造以顶角的顶点为圆心、以腰长为半径的圆,或构造以顶角的顶点为圆心、以底边上的高为半径的圆,或构造以底角的顶点为圆心、以腰长为半径的圆

图5
典例分析3:如图5,点O为正方形ABCD的中心,点G是OA的中点,△EGF是等腰直角三角形,H是EF的中点,∠EGF=90°,AB=2,GE=2,△EGF绕点G按逆时针方向旋转,则旋转过程中BH的取值范围是___________.
【分析与解答】由于△EGF是等腰三角形,所以以点G为圆心、以EG为半径画圆,则点E、F在这个圆上,并且EF是圆的一条弦,H是弦EF的中点.又因为△EGF是腰长为2的等腰直角三角形,连接GH,则GH的长也是一个定值,所以以点G为圆心、以GH的长为半径作圆,很显然,BH的最小值和最大值在直线BG与小圆的交点处取得.如图6,BH1最小,BH2最大.
则BH1=-,BH2=+.

图6
评析:本题中通过旋转等腰△GEF,可以发现EF的中点H到点G的距离是一个定值,所以通过构造以点G为圆心、以GH为半径的圆,进而转化成求圆外一点到圆上的点的最小距离问题,然后连接BG与圆交于点H,从而确定了图形的具体位置,再结合题中的条件,运用已学过的数学知识加以解决.
四、如果遇到两个有公共斜边的直角三角形,可以构造以斜边为直径的圆

图7
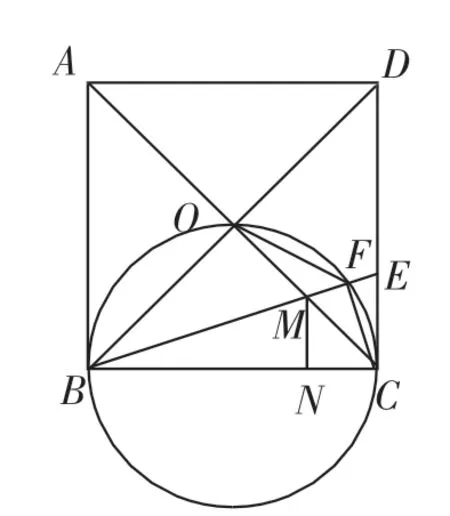
图8
典例分析4:如图7,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE,垂足为点F,连接OF,则OF的长为___________.
【分析与解答】因为四边形ABCD是正方形,所以∠BOC=90°.
由CF⊥BE,得∠BFC=90°,△BOC和△BFC是有公共斜边BC的直角三角形.
很显然,以BC为直径的圆经过点O、F.
由DE=2CE,CD=6,得CE=2,DE=4.
过点M作MN⊥BC于点N.
评析:本题通过构造以BC为直径的圆,得到O、F、B、C四点在同一个圆上.根据圆的有关性质,观察发现△OFM△BCM,下面的关键是求出OM和BM的长,利用相似三角形的性质可以求出OF的长.
总之,构造圆的方法体现了数学发散思维的特点,它能够使数学问题的解题方法打破常规、另辟蹊径、巧妙获解,但是“构造圆”并不是胡思乱想,而是要以牢固掌握的数学基础知识为前提,要以所具备的较强的综合能力为基础,要以敏锐的观察能力为先导,要以良好的分析能力为利器,通过认真、仔细地观察图形,思考问题,分析图形与问题之间的关系,去发现问题的各个环节存在的内在联系,从而为寻求解法创造条件.因此,在遇到几何问题时,一定要沉着冷静、认真思考,根据题中的条件,看看是否符合这几种类型中的某一种类型,然后根据相应的类型构造圆,利用已学过的知识加以解决.

