圆幂定理及其应用*
☉北京市丰台二中 甘志国
圆幂定理在平面几何中有重要应用,相交弦定理与切割线定理都是其重要推论,反过来,用它们也可给出圆幂定理的证明.文章还给出了圆幂定理在解答自主招生试题中的应用.
圆幂定理:若过定点P作一动直线与定圆⊙O(其半径是R)交于A、B两点,则PA·PB=|OP2-R2|(把常数|OP2-R2|叫作定点P对于定圆O的幂).
证明:当点P在⊙O外时,如图1所示,作PT切⊙O于点T,连接OT、OP,可得∠OTP=90°.
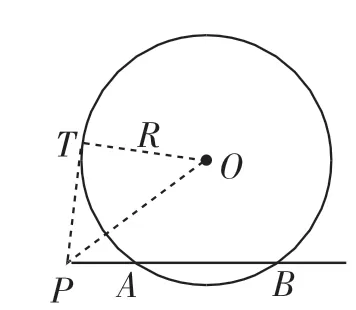
图1
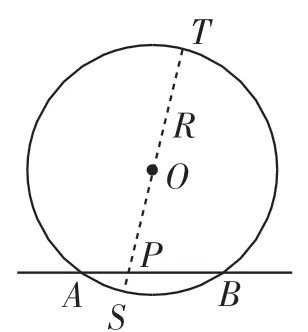
图2
由切割线定理及勾股定理,可得PA·PB=PT2=OP2-R2=|OP2-R2|.
当点P在⊙O上时,不妨设点A与点P重合,可得PA·PB=0=|OP2-R2|.
当点P在⊙O内,即点P在线段AB上且不是端点时,如图2所示,作⊙O过点P的直径ST.
由相交弦定理及勾股定理,可得PA·PB=PS·PT=(R-OP)(R+OP)=R2-OP2=|OP2-R2|.
综上所述,可得欲证结论成立.
注:由该证明可得:也可把圆幂定理的结论用向量表示为
题目:(2013年北京大学暑期体验营数学试题第3题)已知抛物线y=x2+ax+b与坐标轴交于三个两两互异的点A、B、C,且△ABC的外心在直线y=x上,求a+b的值.
解法1:可设点A(x1,0)、B(x2,0)、C(0,b)(b≠0).
因为点A、B均在抛物线y=x2+ax+b上,所以x1、x2是关于x的一元二次方程x2+ax+b=0的两个根.
由于△ABC的外心在直线y=x上,可设△ABC的外接圆方程是x2+y2+mx+my+n=0.由点A、B均在该圆上,可得x1、x2是关于x的一元二次方程x2+mx+n=0的两个根.
所以m=a,n=b.
再由点C(0,b)在圆x2+y2+mx+my+n=0上,可得b2+ab+b=0(b≠0),则a+b=-1.
解法2:可设点A(x1,0)、B(x2,0)、C(0,b)(b≠0).
因为点A、B均在抛物线y=x2+ax+b上,所以x1、x2是关于x的一元二次方程x2+ax+b=0的两个根(因而x1x2=b).
由于△ABC的外心在直线y=x上,可设△ABC的外接圆圆心为.再由圆幂定理的注可 得x1x2=b=,则a+b=-1.
注:本题源于2008年高考江苏卷第18题:
在平面直角坐标系xOy中,设二次函数f(x)=x2+2x+b(x∈R)的图像与两坐标轴共有三个交点,经过这三个交点的圆记为C.
(1)求实数b的取值范围;
(2)求圆C的方程;
(3)问圆C是否经过某定点(其坐标与b无关)?请证明你的结论.

