基于小波降噪的IMU精对准性能分析
张轩轩, 杨诚
(中国地质大学(北京) 土地科学技术学院,北京 100083)
0 引 言
捷联式惯性导航系统(SINS)相对于平台式惯性导航系统具有体积小、成本低等特点,已经广泛应用于各种军民导航领域. SINS通过加速度计和陀螺仪等惯性量测器件,测量载体的加速度和角速度[1]. 系统通过对载体加速度的积分获得速度信息,再次对速度进行积分,获得载体的位置增量信息. 然而,惯性导航系统需要事先获取载体的初始状态信息,包括载体的位置,速度和姿态,初始状态的任何误差都将无条件带入后续的动态导航定位中. 初始状态一般可以通过惯性导航的对准来实现. 惯性导航初始对准中的姿态对准是为了估计载体坐标系相对于参考坐标系的指向,并获得载体坐标系到参考坐标系的旋转矩阵. 该矩阵在导航过程中,将惯性传感器量测到的比力和角速度从载体系投影到参考坐标系中. 因此,对准速度和精度决定了惯性导航系统后续导航精度.
捷联式惯性导航传感器的对准过程可以分为粗对准和精对准两个部分. 粗对准一般采用解析的方法获取姿态角的初始值,然后使用精对准对姿态角进行估计[2-4]. 由于惯性导航系统不依赖外界条件,可以通过自主量测的数据实现自主导航的系统,因此,对于高精度的惯性传感器,可以通过自身量测数据感知地球重力与地球自转,再通过卡尔曼滤波进行精对准,此过程称为自对准[5]. 然而,对于中低精度的惯性传感器,由于自身的噪声较大,无法高精度地量测地球自转,需要通过辅助的观测信息进行精对准. El-Sheimy[6]提出利用多层小波分解法削弱传感器量测数据的高频噪声. 该方法有效提高了对准精度和效率. 目前,精对准一般是基于惯性传感器的小失准角线性误差方程,通过卡尔曼滤波和惯性传感器的小失准角线性误差方程实现的[7]. 本文以高、中、低三种精度的捷联式惯性传感器为研究对象,利用卡尔曼滤波分析比较三种精度的惯性传感器的精对准性能.
1 精对准及小波降噪原理
1.1 坐标系定义
SINS姿态对准的目的是为了获取载体坐标系与参考坐标系之间的关系. 本文的载体坐标系(b)为右前上坐标系, 其原点位于惯性测量装置(IMU)测量中心,x轴指向载体的右方,y轴指向载体运动的方向,z轴指向载体上方,构成右手坐标系. 为了讨论问题方便, 一般令导航坐标系(n)与当地水平坐标系(l)重合; 另一个关注的坐标系是当地水平坐标系,该坐标系为东北天坐标系,其原点为运载体的中心,z轴向上指向天顶,x轴指向地理东向,y轴垂直于x轴与z轴构成的平面成右手坐标系.
(1)
式中,φ、θ、ψ分别表示横滚角、俯仰角和航向角.
1.2 小失准角误差模型
小失准角误差模型是惯性导航系统的经典误差模型,其核心是假设姿态误差角为小角度. 因此,误差方程可以通过在经典惯性导航力学编排的基础上施加小的误差扰动获得[9],如式(2)~(4)所示.

(2)


(3)

(4)
式中,D-1为位置误差方程计算矩阵.
静基座条件下,由于传感器在静止状态下,νn=[0,0,0]T,理论上,位置分量误差为零,因此式(4)可以省略.
因此,取导航坐标系为东北天坐标系时,惯性系统的状态向量为[10]
Xk-1=[φE,φN,φU,δvE,δvN]T,
(5)
式中,δ(·)代表状态的误差,本文以δvE、δvN为观测量.因此,卡尔曼滤波的离散化状态模型为
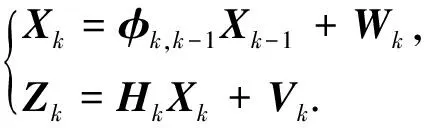
(6)
其中:
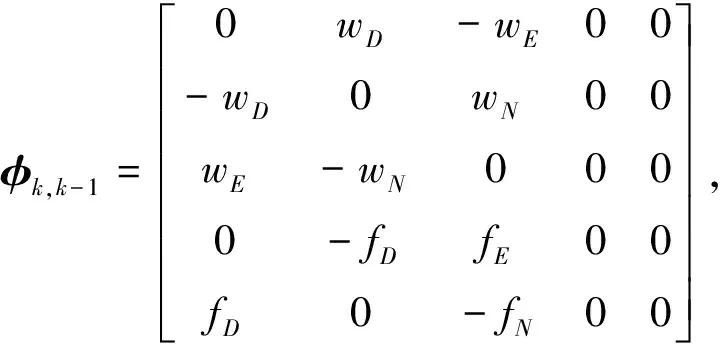
(7)
wN=ΩcosL+vE/R0,
(8)
wE=vN/R0,
(9)
wD=ΩsinL-vEtanL/R0,
(10)
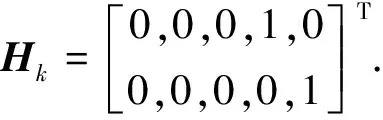
(11)
式中:φk,k-1为卡尔曼滤波的系数转移矩阵;Xk-1为k-1时刻的卡尔曼滤波的状态矢量;Xk为k时刻的卡尔曼滤波的状态矢量;Wk为系统过程的噪声向量;Hk为卡尔曼滤波观测方程的系数矩阵;Vk为速度噪声观测向量;L为当地纬度;Ω为地球自转角速率;R0为地球半径.
1.3 小波降噪

图1 小波分解示意图
2 仿真与实验测试
为了对比分析高中低三种精度的惯性传感器的对准精度,同时考虑到低精度惯性导航器件受外部噪声影响较大,本文采用实测数据和低精度惯性器件仿真数据进行对准性能分析.实测数据由ATLANS、3DM-GX5-25和MPU-6700三种惯性传感器采集,数据采样频率均为100 Hz. 三种传感器的性能参数如表1所示. 同时使用相同参数生成MPU-6700仿真数据进行对比分析.
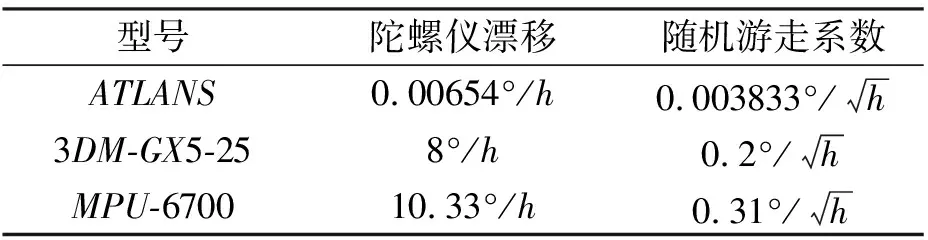
表1 传感器参数
对于数据采样时间通常是由对准所需的时间来决定的,而对准时间与对准所需达到的精度存在以下关系:

(12)
式中:ARW表示角度随机游走;we为地球自转角速度;φ为运载体所在的纬度;δA是方位对准误差;Ta是对准时间. 本文所需要达到的方位对准误差为0.01°/h,通过计算可知,ATLANS对准时间需要4 s,3DM-GX5-25对准时间需要10 903 s,MPU-6700对准时间需要24 532 s. 因此,数据采样时长比对准时间长即可,本文采样时长分别为:10 000 s,11 000 s, 500 000 s.对高频噪声,本文采用文献[11]AB中的函数命令wden,选用db4小波基,分解层数为5. 经小波分析处理后,各个惯性器件的有效输出信号均明显降低,如图2~5所示. 可以发现,MPU-6700去噪后的信号在0~500000 s间有明显的非线性特征,这是仿真数据和另外两种传感器输出的数据所没有的.
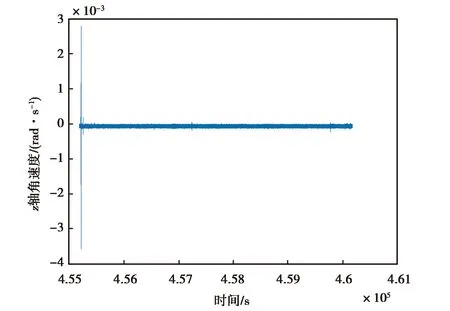
(a) ATLANS z轴角速度降噪前变化图
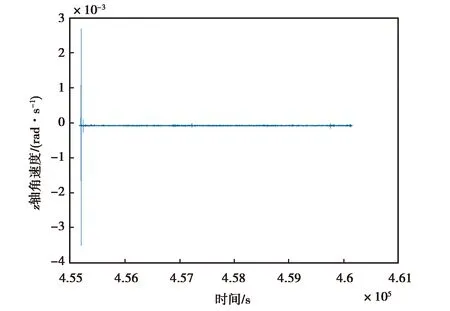
(b) ATLANS z轴角速度降噪前变化图图2 ATLANS z轴角速度降噪前后变化图
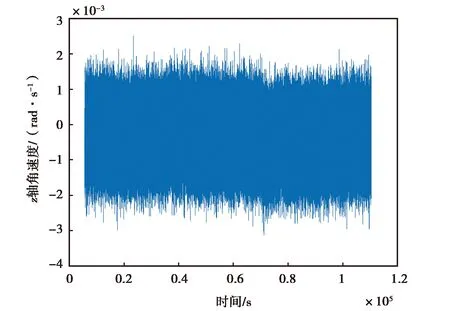
(a) 3DM-GX5-25 z轴角速度降噪前变化图
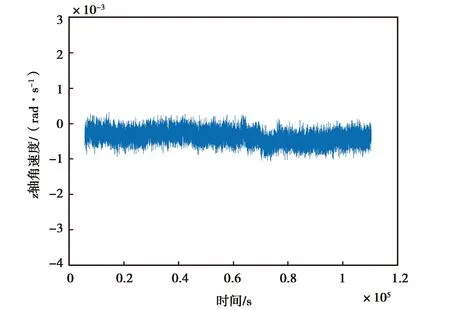
(b) 3DM-GX5-25 z轴角速度降噪后变化图图3 3DM-GX5-25 z轴角速度降噪前后变化图
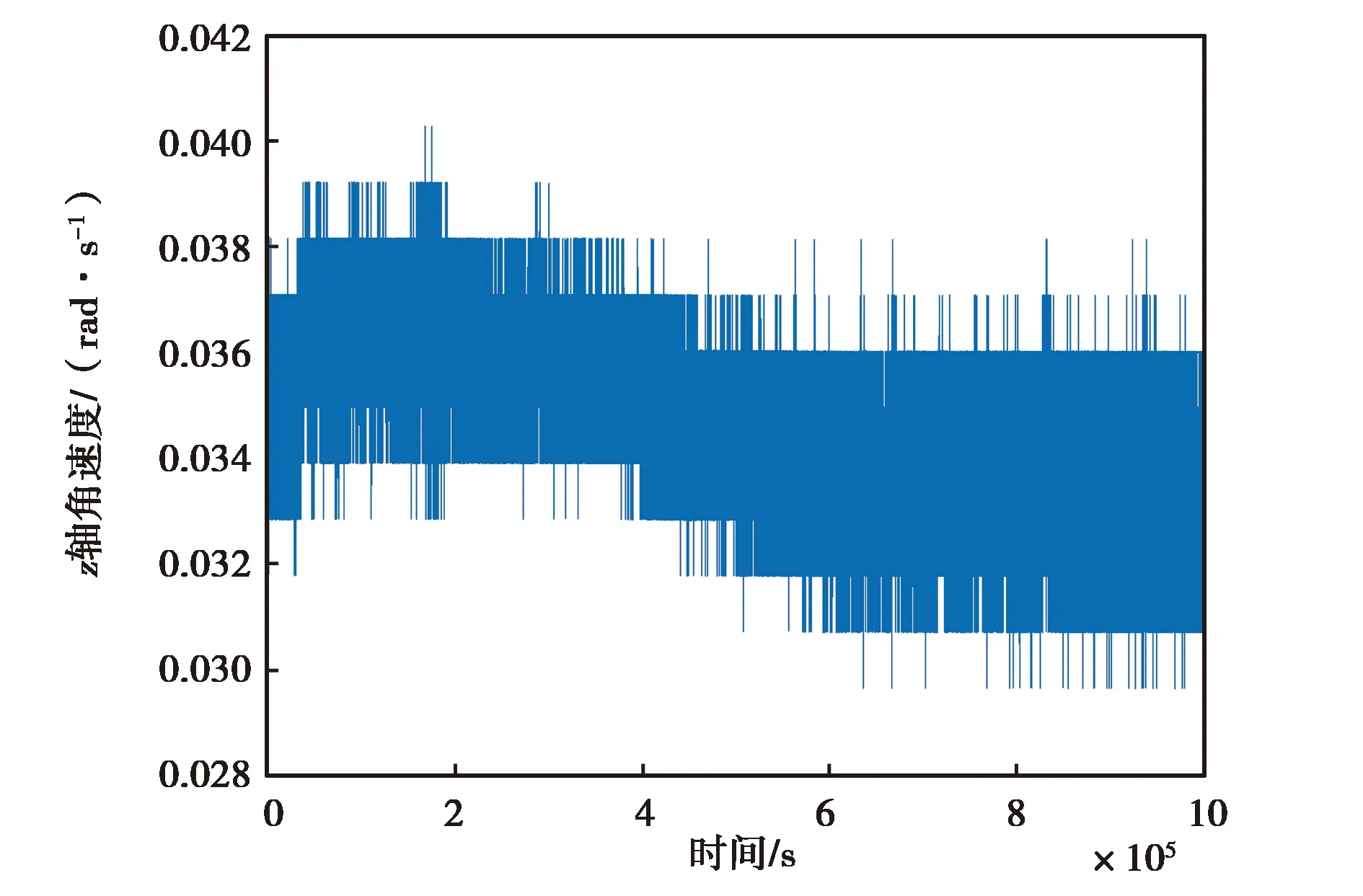
(a) MPU-6700 z轴角速度降噪前变化图

(b) MPU-6700仿真z轴角速度降噪后变化图图5 MPU-6700仿真z轴角速度降噪前后变化图
对3个惯性器件的实测数据与MPU-6700仿真数据进行功率谱分析,由于陀螺仪的精度对惯性导航的导航精度影响较大,本文选取各个惯性器件陀螺仪的z轴输出角速度进行研究,各个数据的功率谱分析如图6~9所示.
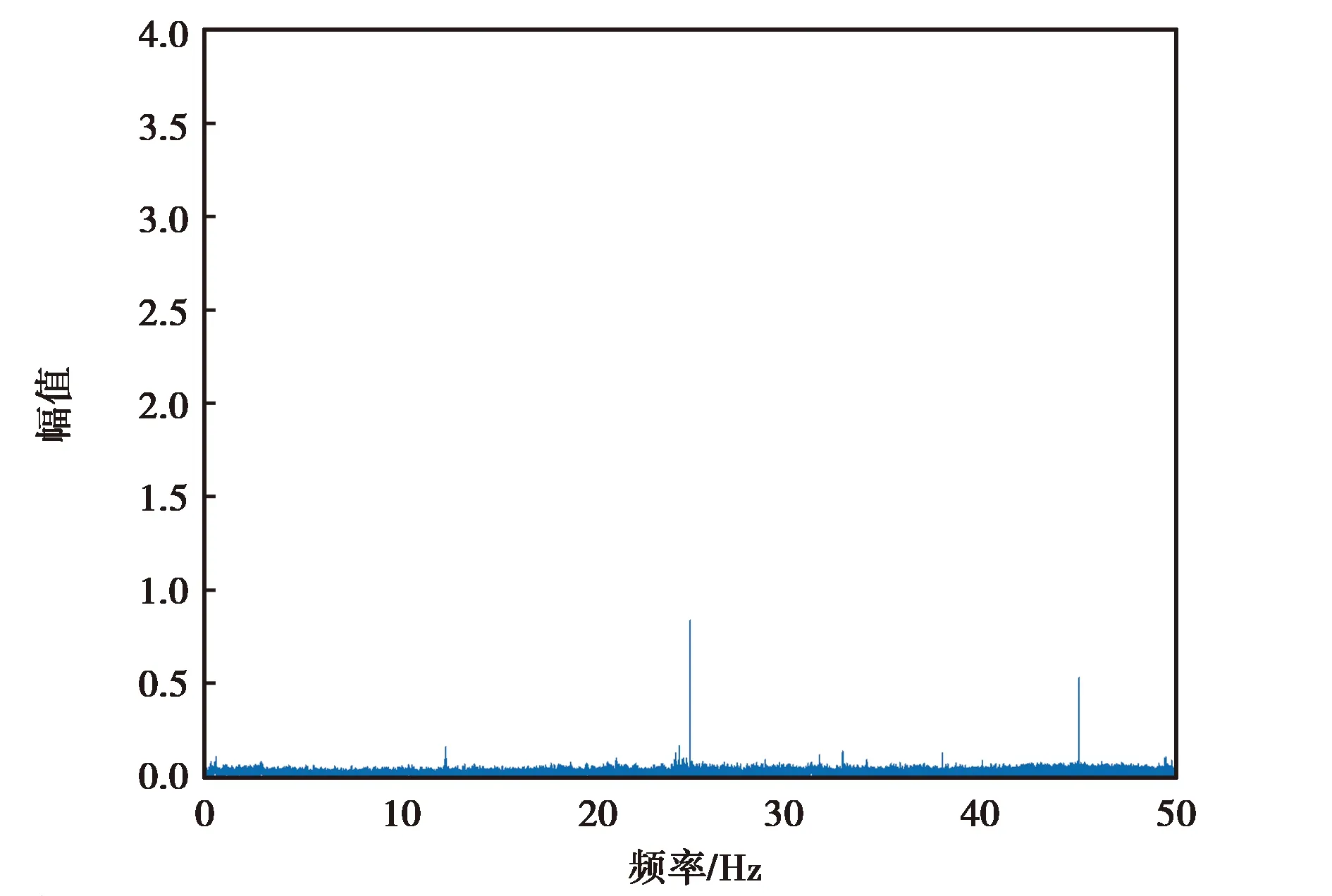
(a) ATLANS z轴角速度降噪前频谱分析图

(b) ATLANS z轴角速度降噪后频谱分析图图6 ATLANS z轴角速度降噪前后频谱分析图
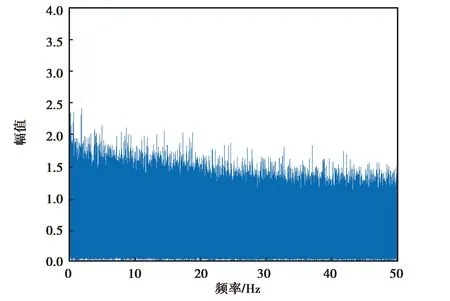
(a) 3DM-GX5-25 z轴角速度降噪前频谱分析图
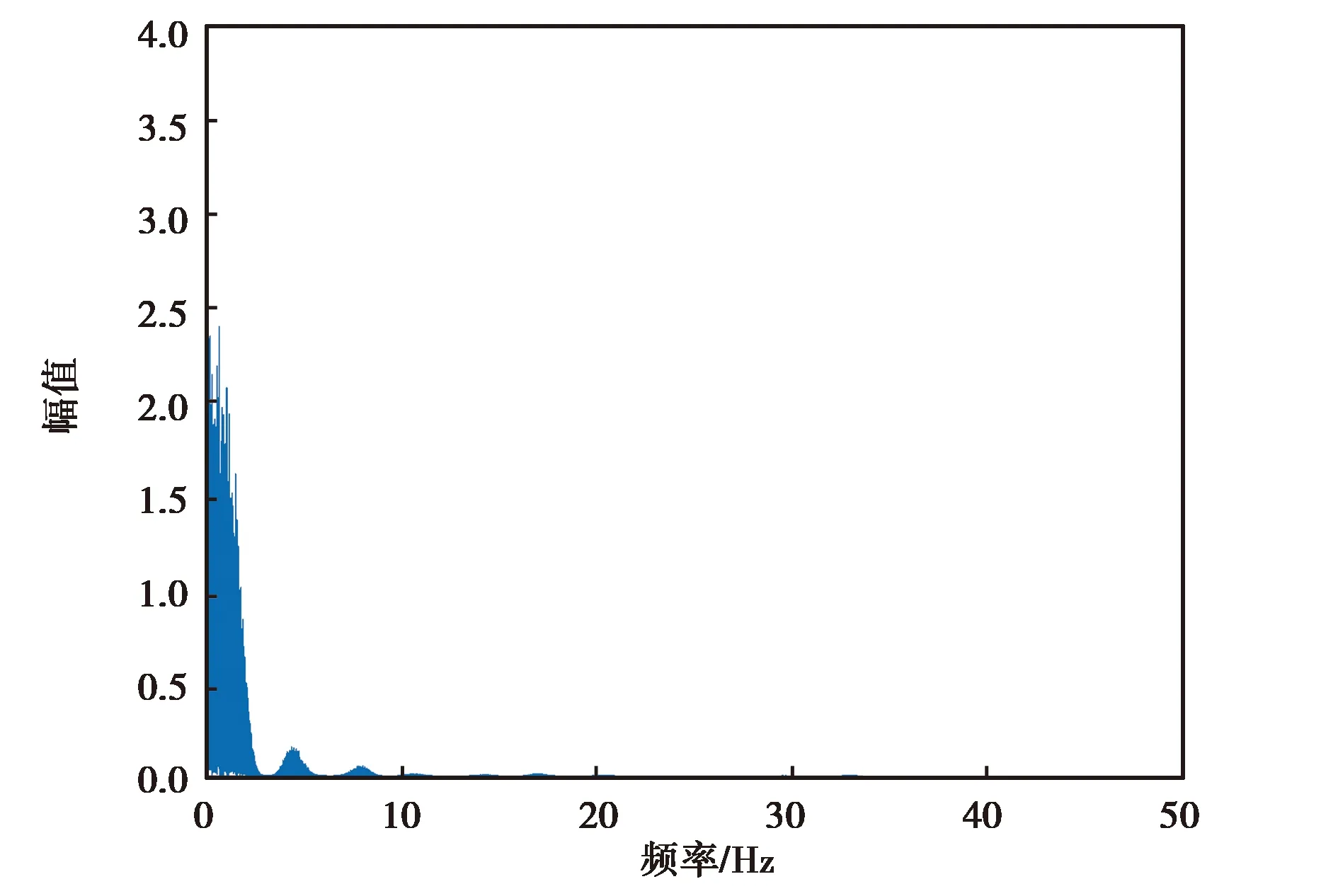
(b) 3DM-GX5-25 z轴角速度降噪后频谱分析图图7 3DM-GX5-25 z轴角速度降噪前后频谱分析图
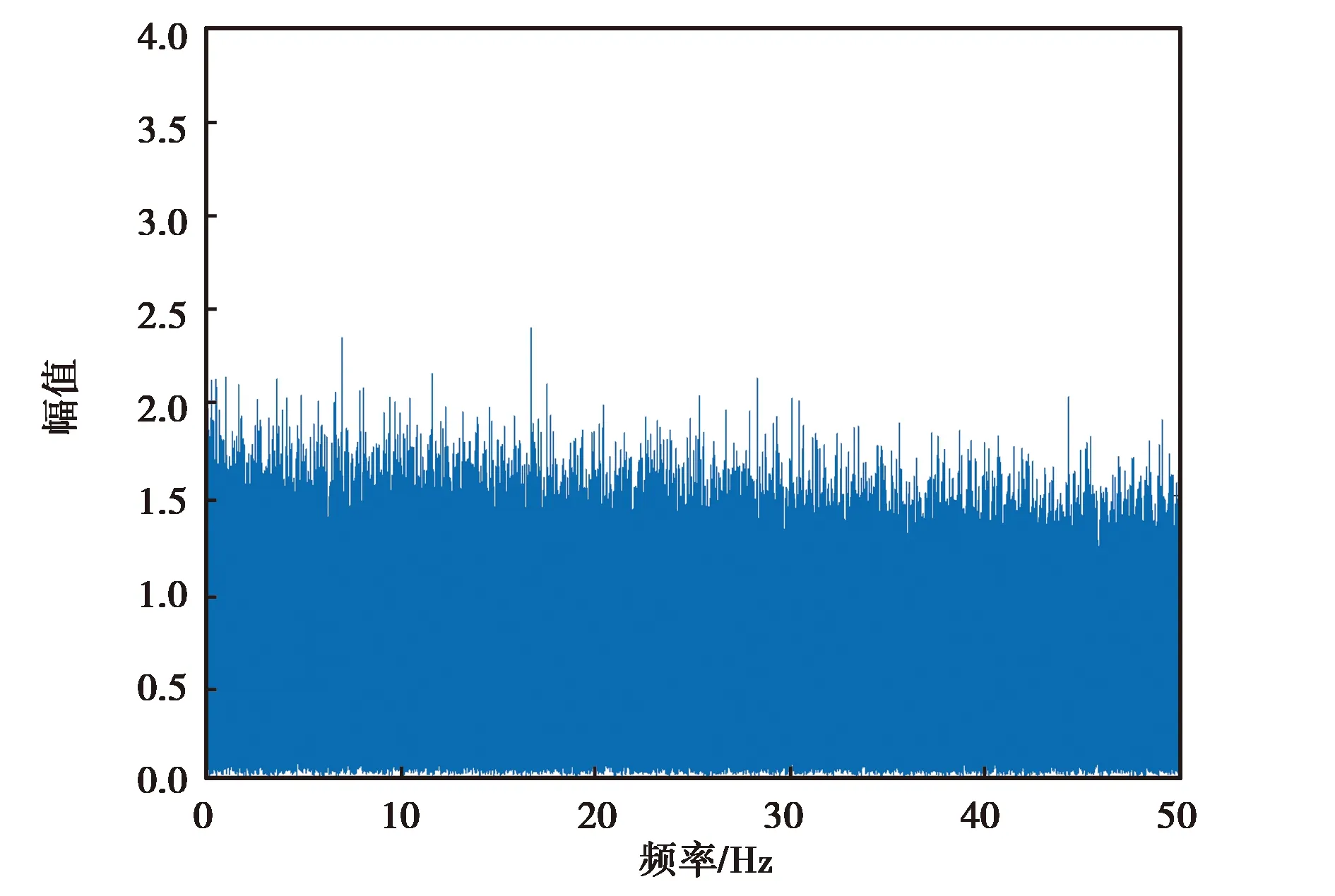
(a) MPU-6700 z轴角速度降噪前频谱分析图

(b) MPU-6700 z轴角速度降噪后频谱分析图图8 MPU-6700 z轴角速度降噪前后频谱分析图
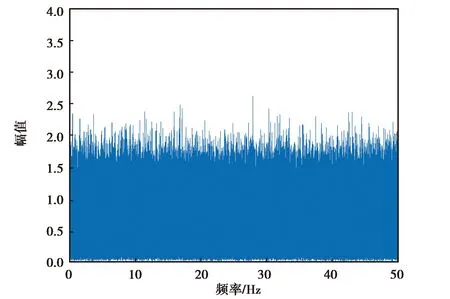
(a) MPU-6700仿真z轴角速度降噪前频谱分析图
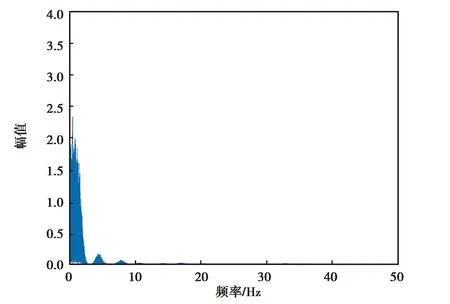
(b) MPU-6700仿真z角速度降噪后频谱分析图图9 MPU-6700仿真z轴角速度降噪前后频谱分析图
由图6~9可知,各个惯性器件在小波降噪前的高频噪声比较大,但经过小波分析处理,其高频噪声得到了有效抑制,保留了低频有效信息.
数据经小波降噪后,通过粗对准获取姿态角的初值,如表2所示.
一个完善的制度体系可以给管理者们起到良好的辅助作用,更可以让员工约束其自身,促进工程进度,打消员工消极怠工的状态,增强团队的管理体系,完善制度从以下几方面入手:
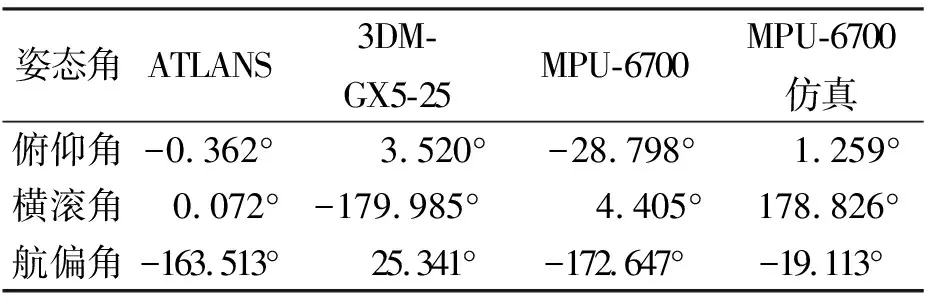
表2 粗对准姿态角
最后利用卡尔曼滤波精对准的方法进行姿态的解算,得到三种惯性器件姿态角随时间的变化情况.进行卡尔曼滤波精对准时三种惯性器件的滤波初始状态均为X=[10°,10°,10°,0°,0°]T,惯性器件ATLANS的状态协方差矩阵为
P=diag((0.00625°/h)2,(0.00625°/h)2,(0.00625°/h)2,(100 μg)2,(100 μg)2),动力学模型噪声矩阵为
Q=diag((0.009899°/h)2,(0.009899°/h)2,(0.009899°/h)2,(50 μg)2,(50 μg)2);
3DM-GX5-25状态协方差矩阵为
P=diag((8°/h)2,(8°/h)2,(8°/h)2,(200 μg)2,(200 μg)2);
动力学模型噪声矩阵为
Q=diag((1.2°/h)2,(1.2°/h)2,(1.2°/h)2,(180 μg)2,(180 μg)2);
惯性器件MPU-6700状态协方差矩阵为
P=diag((10.33°/h)2,(10.33°/h)2,(10.33°/h)2,(3300 μg)2,(3300 μg)2);
动力学模型噪声矩阵为
Q=diag((1.8°/h)2,(1.8°/h)2,(1.8°/h)2,(2880 μg)2,(2880 μg)2).
上述矩阵P和Q中前3项分别为各惯性器件陀螺仪的零偏和随机误差,后两项为加速度计的零偏和随机误差.
仿真数据及实测数据的对准结果如图10~13所示.
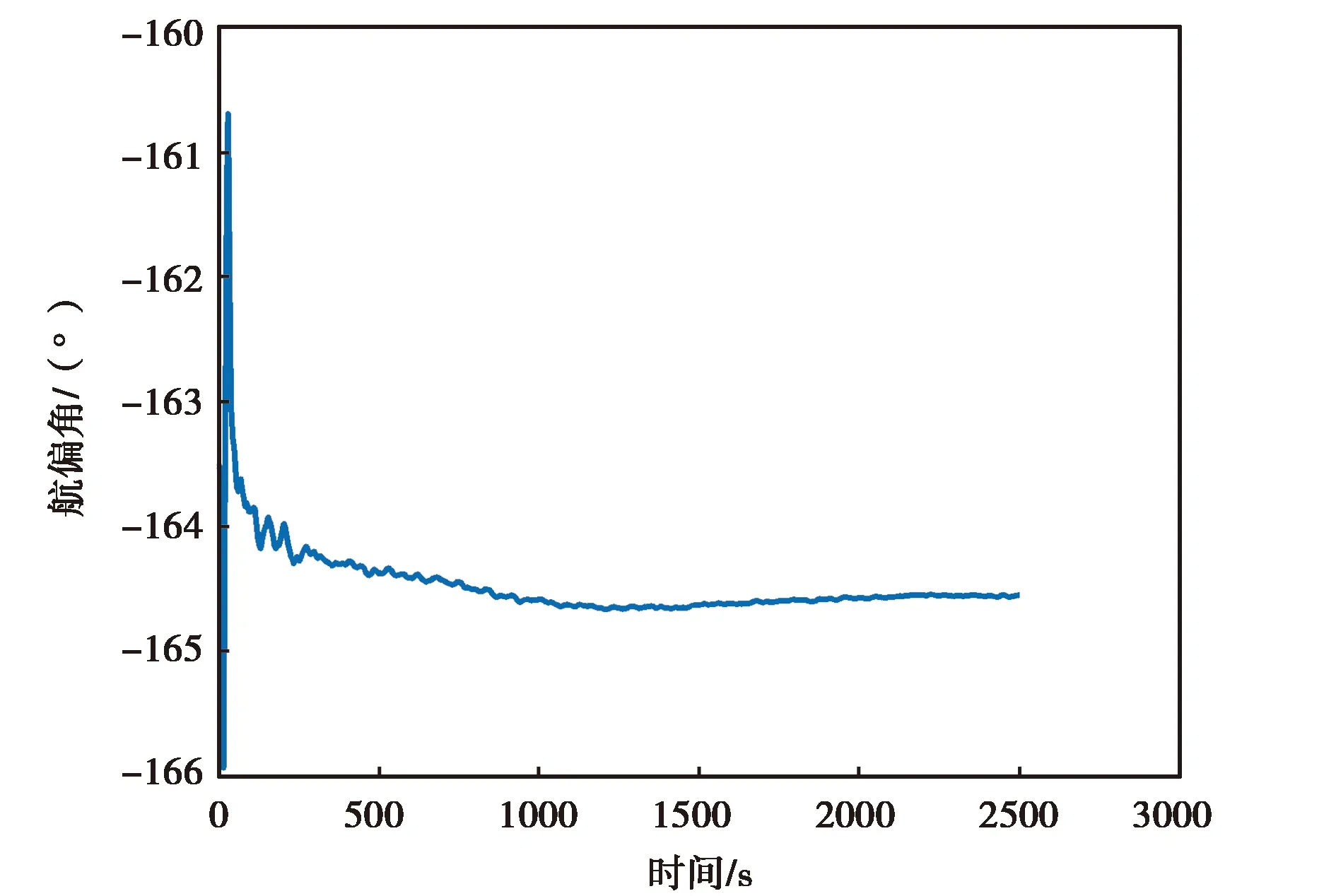
(a) ATLANS航偏角变化图
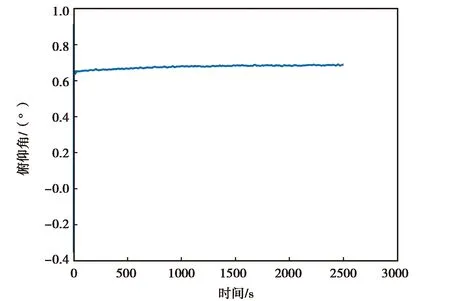
(b) ATLANS俯仰角变化图
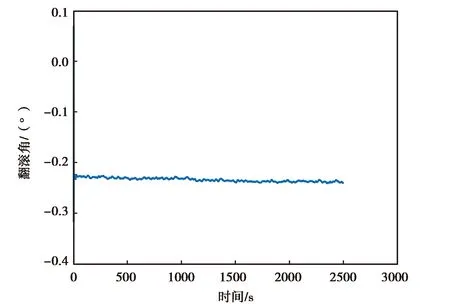
(c) ATLANS翻滚角变化图图10 ATLANS实测数据精对准结果图
图10示出的是ATLANS实测数据进行卡尔曼滤波精对准的姿态结果.由图10(a)、(b)、(c)可知,ATLANS惯性器件的姿态角在最开始的时候是发散的,但是经过一段时间后开始收敛到固定的角度或固定角度附近,收敛的一致性比较好.

(a) 3DM-GX5-25航偏角变化图
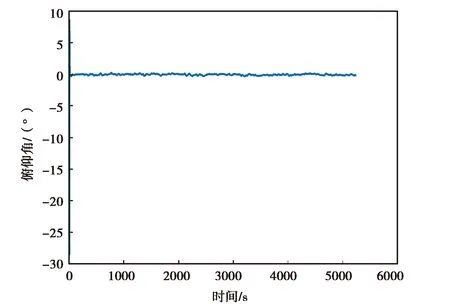
(b) 3DM-GX5-25俯仰角变化图
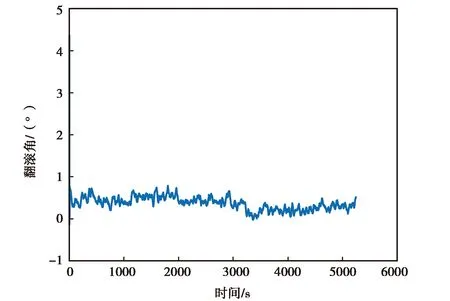
(c) 3DM-GX5-25翻滚角变化图图11 3DM-GX5-25实测数据精对准结果图
图11示出的是3DM-GX5-25实测数据和精对准的姿态结果,由图11(a)、(b)、(c)可知,3DM-GX5-25惯性器件的姿态角最后均收敛到了一个固定角度或其附近,但可以明显看到,其收敛速度慢,同时其翻滚角收敛时仍存在较ATLANS的翻滚角大的震动.
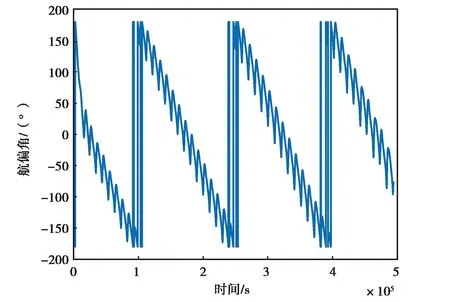
(a) MPU-6700航偏角变化图

(b) MPU-6700俯仰角变化图
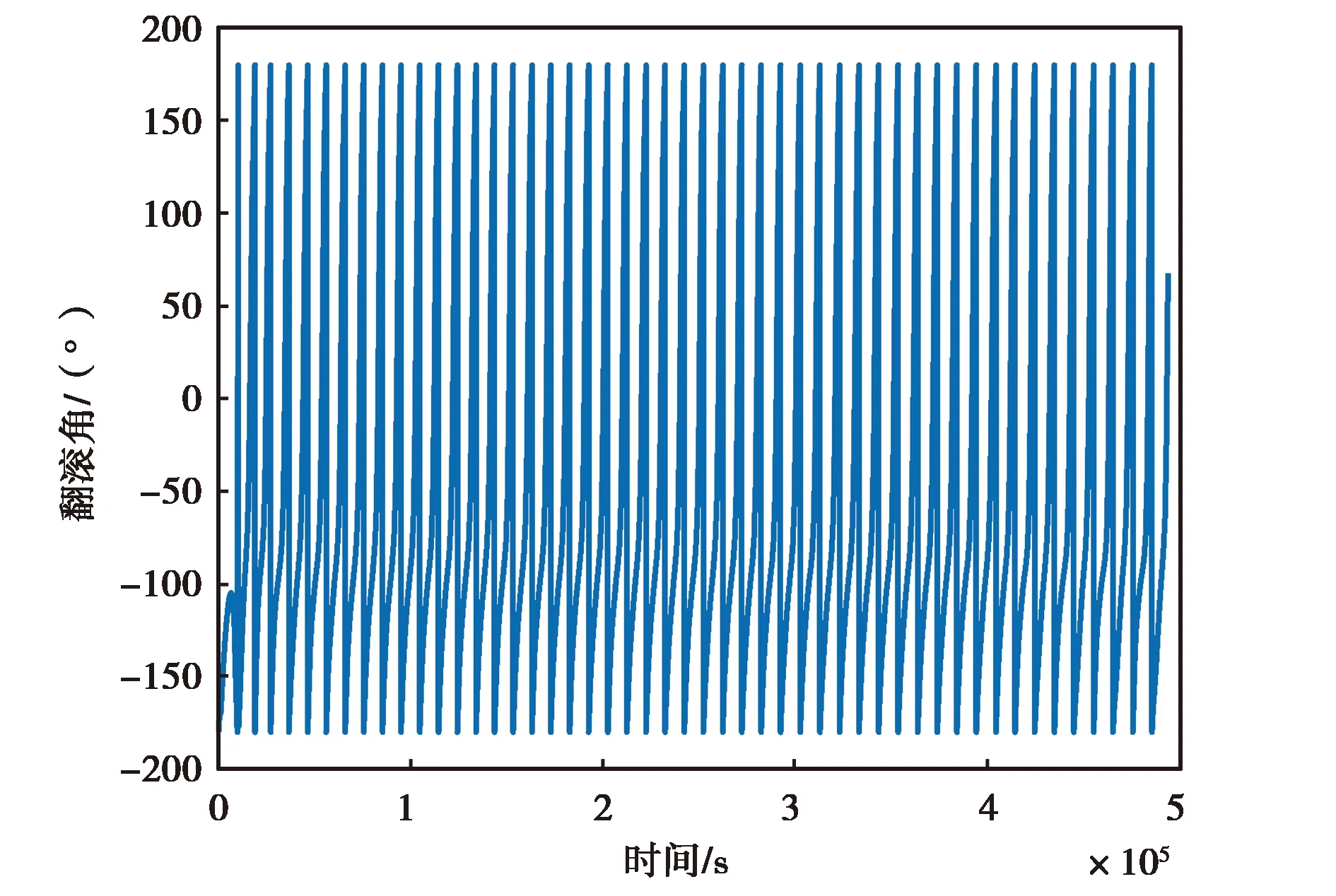
(c) MPU-6700翻滚角变化图图12 MPU-6700实测数据精对准结果图
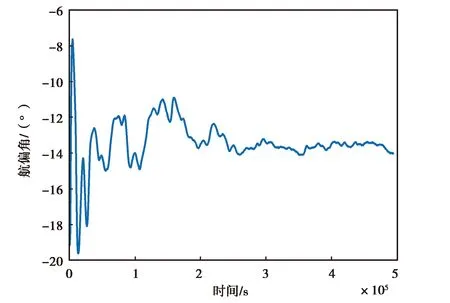
(a) MPU-6700仿真数据航偏角变化图
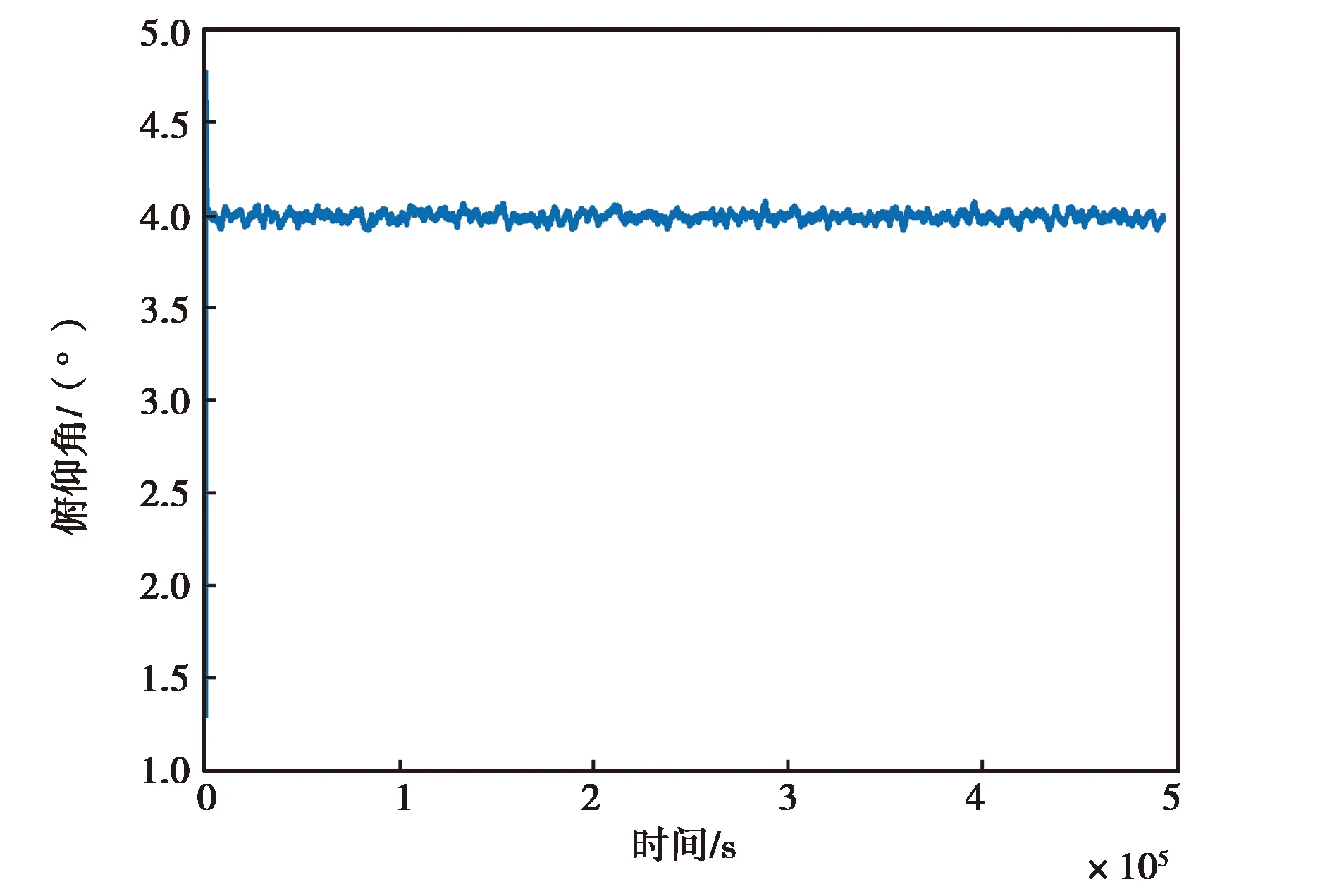
(b) MPU-6700仿真数据俯仰角变化图
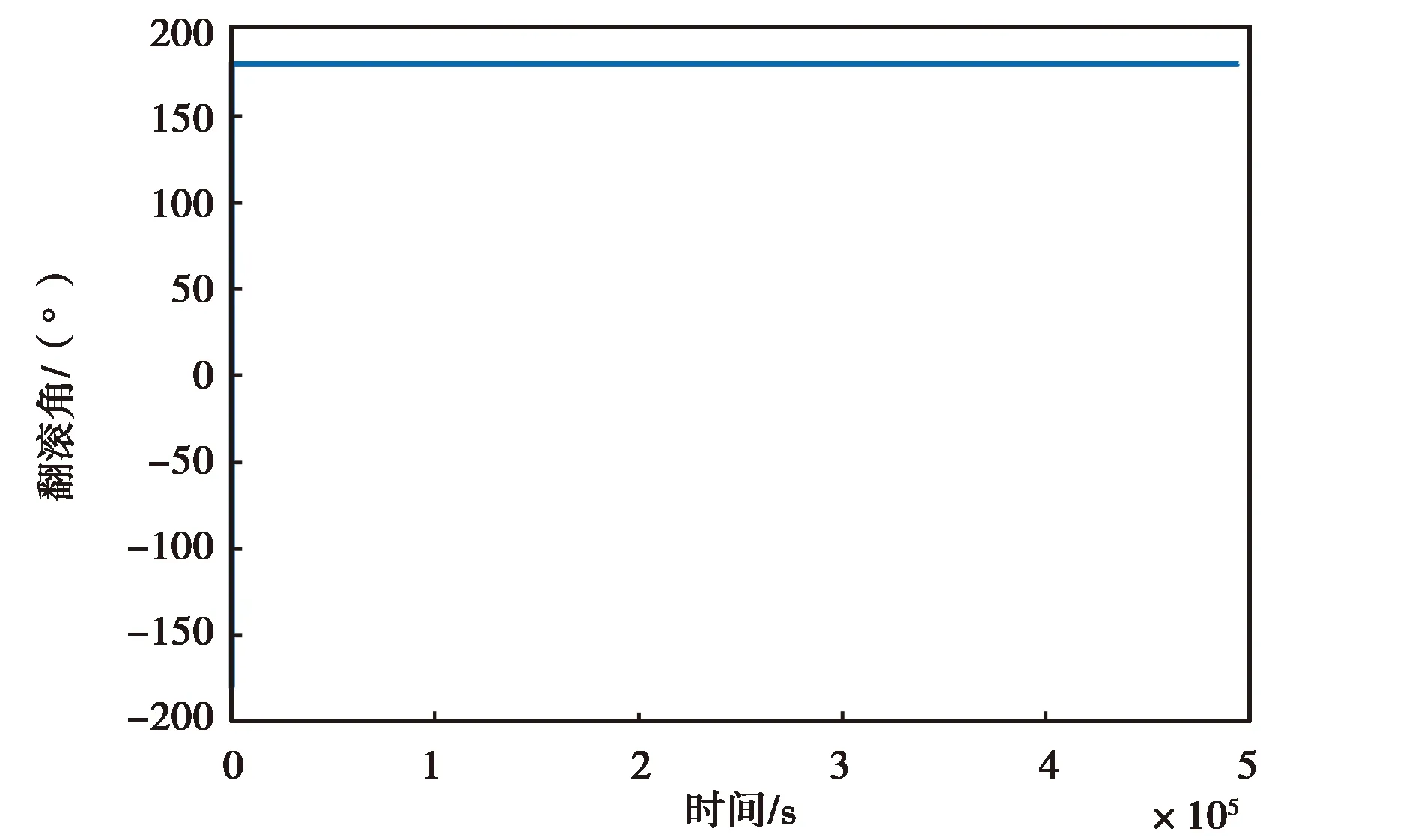
(c) MPU-6700仿真数据翻滚角变化图图13 MPU-6700仿真数据精对准结果图
图12和图13示出的是MPU-6700实测数据和仿真数据的精对准结果图,由图12(a)、(b)、(c)可以直观看出,MPU-6700惯性器件的三个姿态角随时间的变化在不断振荡,最终无法收敛,而由图13可以看出仿真数据能够最终收敛于固定的角度附近.造成该现象的原因是低精度传感器不仅仅受到白噪声的影响,而且受其他复杂特性误差的影响(如非线性误差),其数据的低频分量有着明显的非线性特性. 而仿真数据受到的干扰单一,能够快速收敛.
综合图10、11、12,由图10(a),图11(a),图12(a)可以清楚地看到ATLANS的航偏角很快收敛到了一个固定角度的附近,3DM-GX5-25的航偏角则用了相对较长的时间才收敛,MPU-6700的航偏角则完全振荡、发散;由图10(b),图11(b),图12(b)可以看出ATLANS和3DM-GX5-25的俯仰角均较快收敛到了各自固定角度附近,而MPU-6700的航偏角则依旧振荡、发散;由图10(c),图11(c),图12(c)可以看出ATLANS和3DM-GX5-25的翻滚角均收敛到了各自固定角度附近,但3DM-GX5-25翻滚角的振荡较ATLANS的翻滚角剧烈,MPU-6700的翻滚角则依旧振荡、发散.
3 结束语
论文通过卡尔曼滤波对低、中、高三种不同性能的惯性导航器件进行基于以小波分析的精对准性能分析,最后对精对准结果的三个姿态角进行对比分析,得到如下结论:
1)小波分析方法可以有效抑制噪声信号影响,提取出对精对准有用的信号,去噪效果明显.
2)性能较好的惯性导航器件其精对准的速度较快,性能较差的惯性导航器件精对准的速度较慢.
3)性能高的惯性传感器有着较好的对准精度;而低精度的传感器,由于噪声及误差的原因,对准精度较低,甚至出现滤波发散情况.
4)性能较低的惯性传感器由于受复杂特性误差的影响无法对准,而采用相同噪声参数仿真的数据可以实现较好的对准.

